【知识点】图与图论入门
何为图论
见名知意,图论 (Graph Theory) 就是研究 图 (Graph) 的数学理论和方法。图是一种抽象的数据结构,由 节点 (Node) 和 连接这些节点的 边 (Edge) 组成。图论在计算机科学、网络分析、物流、社会网络分析等领域有广泛的应用。
如下,这就是一个图,可以看到这个图有 5 5 5 个顶点,分别编号为 { 0 , 1 , 2 , 3 , 4 } \{0, 1, 2, 3, 4\} {0,1,2,3,4}。同时这个图有 4 4 4 条边,例如,在顶点 2 2 2 和 顶点 4 4 4 之间存在着一条边。

图的基本概念
在详细讲解图论和有关图论算法之前,先来了解一下在图论中的一些基本表述和规范。
- 图 (Graph):图是一种由一组顶点和一组边组成的数据结构,记做 G = ( V , E ) G = (V, E) G=(V,E),其中 V V V 代表顶点集合, E E E 代表边集合。
- 顶点 (Vertex):顶点是图的基本单位,也称为节点。
- 边 (Edge):一条边是连接两个顶点的线段或弧。可以是无向的,也可以是有向的。一条边可以记做为 ( u , v ) (u, v) (u,v)。在无向图中,若存在一条 ( u , v ) (u, v) (u,v),表示可以从 u u u 点直接走到 v v v 点,反之亦然。但若在有向图中,存在一条边 ( u , v ) (u, v) (u,v),表示可以从 u u u 节点直接走向 v v v 节点,如果不存在一条边 v , u v, u v,u,那么 v v v 节点就没有办法直接走向 u u u 节点。
- 无向图 (Undirected Graph):图中的边没有方向,即 ( u , v ) (u, v) (u,v) 和 ( v , u ) (v, u) (v,u) 是同一条边。
- 有向图 (Directed Graph/ Digraph):图中的边有方向,即 ( u , v ) (u, v) (u,v) 和 ( v , u ) (v, u) (v,u) 不是同一条边。
- 简单图 (Simple Graph):表示含有重边(两个顶点之间的多条边)和自环(顶点到自身的边)的图。
- 多重图 (Multigraph):允许有重边和自环的图。
- 边权 (Weight of an Edge):一般表示经过这一条边的代价(代价一般是由命题人定义的)。
如下图,就是一个有向的简单图(通常来说,在有向图中边的方向用箭头来表示):

如下图,就是一个无向的多重图,其中存在两条边可以从顶点 5 5 5 到顶点 2 2 2:

与此同时,为了方便起见,对于无向图的处理,我们只需要在两个顶点之间建立两个方向相反的无向边就可以表示一个无向图,具体如下:

图的表示方法
在计算机中,图可以通过许多方式来构建和表示。总的可以分成图的邻接矩阵和邻接表两种方法(关于链式前向星本文不过多展开叙述,有兴趣的可以自行查阅相关文档)。
图的邻接矩阵 (Adjacency Matrix)
若一个图中有 N N N 个顶点,那么我们就可以用一个 N × N N \times N N×N 的矩阵来表示这个图。我们一般定义,若矩阵的元素 A i , j ≠ − ∞ A_{i, j} \neq -\infty Ai,j=−∞ 表示从节点 i i i 到 j j j 有一条有向边,其中边的权值为 A i , j A_{i, j} Ai,j。
假设存在一个有 3 3 3 个顶点的图,并且有三条有向边 E = { ( 1 , 2 ) , ( 2 , 3 ) , ( 3 , 2 ) } E = \{(1, 2), (2, 3), (3, 2)\} E={(1,2),(2,3),(3,2)},那么就可以用邻接矩阵表示为:
G = [ 1 2 3 1 0 1 0 2 0 0 1 3 0 1 0 ] G = \begin{bmatrix} & \mathtt{1} & \mathtt{2} & \mathtt{3}\\ \mathtt{1} & 0 & 1 & 0 \\ \mathtt{2} & 0 & 0 & 1 \\ \mathtt{3} & 0 & 1 & 0 \end{bmatrix} G= 123100021013010
画成可视化的图就长这个样子:

在 C++ 中,我们可以简单地用一个二维数组来表示:
// 定义一个矩阵。
int map[50][50];// 将所有的边初始化为负无穷大。
for (int i=1; i<=50; i++)for (int j=1; j<=50; j++)map[i][j] = -0x7f7f7f7f;// 建边,其中所有的边权为1。
map[1][2] = map[2][3] = map[3][2] = 1;
图的邻接表 (Adjacency List)
邻接表本质上就是用链表表示图。数组的每个元素表示一个顶点,元素的值是一个链表,链表中存储该顶点的所有邻接顶点。假设存在一个有 4 4 4 个顶点的图,并且有四条有向边 E = { ( 1 , 2 ) , ( 2 , 3 ) , ( 3 , 2 ) , ( 3 , 4 ) } E = \{(1, 2), (2, 3), (3, 2), (3, 4)\} E={(1,2),(2,3),(3,2),(3,4)},那么就可以用邻接表表示为:

画成可视化的图就长这个样子:

在 C++ 中,我们可以使用 STL模板库 中的 vector 来实现:
#include <vector>
vector<int> G[50]; // 建图。
G[1].push_back(2);
G[2].push_back(3);
G[3].push_back(2);
G[3].push_back(4);
一般情况下,推荐使用邻接表的方式来存图,因为使用邻接矩阵比较浪费空间。在顶点数量非常多但边非常少的图中, N 2 N^2 N2 的时空复杂度会导致 MLE 或 TLE 等问题。
图的各种性质
- 度数 (Degree):一个顶点的度是连接该顶点的边的数量。在有向图中,有 入度 (Indegree) 和 出度 (Outdegree) 之分(具体例子见后文)。
- 路径 (Path):从一个顶点到另一个顶点的顶点序列,路径上的边没有重复。
- 回路 (Cycle):起点和终点相同的路径。
- 连通图 (Connected Graph):任意两个顶点之间都有路径相连的无向图。
- 强连通图 (Strongly Connected Graph):任意两个顶点之间都有路径相连的有向图。
对于下面这个无向图不连通图,顶点 1 1 1 的度数为 1 1 1;顶点 2 2 2 的度数为 2 2 2;顶点 3 3 3 的度数为 1 1 1;顶点 4 4 4 的度数为 0 0 0。同时,由于 4 4 4 号顶点没有度数,所以该顶点没有办法到达任何一个其他的顶点,所以这个图是一个不连通图:

如下图,就是一个有向不强连通图。其中,顶点 1 1 1 的入度为 0 0 0,出度为 2 2 2;顶点 2 2 2 的入度为 1 1 1,出度也为 1 1 1;顶点 3 3 3 的入度为 2 2 2,但出度为 0 0 0。由于顶点 1 1 1 和顶点 2 2 2 可以走到顶点 3 3 3,但顶点 3 3 3 没有办法走到顶点 1 1 1 或顶点 2 2 2,因此下面的图不是一个强连通图:

对于下图来说, 1 → 2 → 3 → 4 1\to 2\to 3\to 4 1→2→3→4 是一条从顶点 1 1 1 到顶点 4 4 4的路径。 2 → 3 → 4 → 2 → 3 2\to 3\to 4 \to 2\to 3 2→3→4→2→3 就不是一个路径,因为相同的边 ( 2 , 3 ) (2, 3) (2,3) 被多次走到了。 1 → 2 → 3 → 1 1\to 2\to 3\to 1 1→2→3→1 就是一个回路,因为这个路径的起点和终点相同:

图的遍历
图通常采用 深度优先搜索/ 广度优先搜索 这两个算法来遍历。其中深度优先算法是最常见的遍历算法。
对于一个用 邻接矩阵 保存的图,其深度优先搜索遍历的 C++ 代码如下:
int vis[105], map[105][105];void dfs(int node){if (vis[node]) return ;vis[node] = 1;cout << node << endl;for (int i=1; i<=n; i++)if (map[node][i] != -0x7f7f7f7f)dfs(i);return ;
}// 函数调用:dfs(1); 表示从1号顶点开始遍历。
对于一个用 邻接表 保存的图,其深度优先搜索遍历的 C++ 代码如下:
#include <vector>
vector<int> G[105];
int vis[105];void dfs(int node){if (vis[node]) return ;vis[node] = 1;cout << node << endl;for (int to : G[node])dfs(to);return ;
}// 函数调用:dfs(1); 表示从1号顶点开始遍历。
广度优先搜索的方式也类似:
#include <queue>
vector<int> G[105];
int vis[105];void bfs(int node){queue<int> que;que.push(node);while(!que.empty()){int t = que.front();cout << t << endl;que.pop();for (int to : G[node]){if (!vis[to]) {vis[to] = 1;que.push(to);}}}return ;
}// 函数调用:bfs(1); 表示从1号顶点开始遍历。
对于判断无向图的连通性,我们只需要从任意一个点开始跑一遍深搜或者广搜就行了。如果所有顶点的 vis 都被标记了,则证明图是联通的,否则图就是不连通的。
例题讲解
P3916 图的遍历
模板题目,从每一个顶点开始用深搜遍历一遍就可以了。但从每一个点考虑能走到的最大点比较麻烦,一个更优的解决办法是反向建边,从最大的点开始遍历,这样子就可以一次性计算出多个结果。
#include <iostream>
#include <algorithm>
#include <vector>
#include <cstring>
using namespace std;const int N = 10005;
int n, m, ans, vis[N];
vector<int> G[N];void dfs(int node, int d){if (vis[node]) return ;vis[node] = d;ans = max(node, ans);for (int to : G[node]) dfs(to, d);return ;
}int main(){cin >> n >> m;for (int i=0, u, v; i<m; i++){cin >> u >> v;G[v].push_back(u); // 反向建边。}for (int i=n; i>=1; i--) dfs(i, i);for (int i=1; i<=n; i++) cout << vis[i] << ' ';return 0;
}
P5318 【深基18.例3】查找文献
也是一道模板题目,正常遍历即可。
#include <iostream>
#include <algorithm>
#include <vector>
#include <queue>
using namespace std;
const int MAXN = 100005;int n, m;
int vis1[MAXN], vis2[MAXN];
queue<int> que;
vector<int> G[MAXN];void dfs(int node, int current){vis1[node] = 1;cout << node << ' ';if (current == n) return ;for (int i=0; i<G[node].size(); i++){if (vis1[G[node][i]]) continue;dfs(G[node][i], current+1);}return ;
}void dfs(int node){vis2[node] = 1;que.push(node);while(que.size()){int t = que.front();cout << t << " ";for (int i=0; i<G[t].size(); i++){if (vis2[G[t][i]]) continue;vis2[G[t][i]] = 1;que.push(G[t][i]);}que.pop();}return ;
}int main(){cin >> n >> m;for (int i=0; i<m; i++){int t1, t2;cin >> t1 >> t2;G[t1].push_back(t2);}for (int i=1; i<=n; i++) sort(G[i].begin(), G[i].end());dfs(1, 0), cout << endl, dfs(1);return 0;
}
番外 - 图的常见算法
更多关于图论的算法,请持续关注后续更新。
- 深度优先搜索 (DFS):适用于遍历图和检测图中的回路。
- 广度优先搜索 (BFS):适用于寻找最短路径(无权图)。
- Dijkstra 算法:适用于加权图中寻找单源最短路径。
- Bellman-Ford 算法:适用于有负权边的图中寻找单源最短路径。
- Floyd-Warshall 算法:适用于寻找所有顶点对之间的最短路径。
- Kruskal 算法:用于求解最小生成树 (MST - Minimum Spanning Tree)。
- Prim 算法:另一种求解最小生成树的方法。
- 拓扑排序 (Topological Sorting):适用于有向无环图 (DAG),用于任务调度等应用。
- Tarjan 算法:用于求解图中的强连通分量、割点、桥。
相关文章:

【知识点】图与图论入门
何为图论 见名知意,图论 (Graph Theory) 就是研究 图 (Graph) 的数学理论和方法。图是一种抽象的数据结构,由 节点 (Node) 和 连接这些节点的 边 (Edge) 组成。图论在计算机科学、网络分析、物流、社会网络分析等领域有广泛的应用。 如下,这…...

FPGA系列,文章目录
前言 FPGA(Field-Programmable Gate Array,现场可编程门阵列)是一种集成电路,其内部结构可以通过软件重新配置来实现不同的逻辑功能。与传统的ASIC(Application-Specific Integrated Circuit,专用集成电路…...

PAT乙级1003我要通过的做题笔记
分析题意 得到“答案正确”的条件是: 字符串中必须仅有 P、 A、 T这三种字符,不可以包含其它字符; 任意形如 xPATx 的字符串都可以获得“答案正确”,其中 x 或者是空字符串,或者是仅由字母 A 组成的字符串࿱…...

【React】React常用开发工具
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 前言一、React DevTools二、Redux DevTools三、Create React App 前言 React 是一种用于构建用户界面的流行 JavaScript 库,由于其灵活性、性能和可重用…...

Ubuntu20.04编译安装Carla全过程
前言 Carla的安装是我现阶段解决的第一个问题,现记录一下我安装Carla的过程以及我在安装过程中遇到的一些问题。 一、安装前准备 1、硬件环境 carla是一款基于UE4开发的模拟仿真软件,本身对硬件的要求比较高。 我是windows与ubuntu双系统࿰…...

Dijkstra 算法 是什么?
Dijkstra 算法 Dijkstra 算法是一种经典的最短路径算法,用于在图(有向或无向图)中找到从起点到其他所有节点的最短路径。它以广度优先搜索的方式,逐步扩展到目标节点,确保计算出的路径是最短的。 1. Dijkstra 算法的基…...

英文输入法---华为OD机试2024年E卷
题解: 代码:...

理解 package.json 中版本号符号
今天,聊一聊在前端开发中, package.json 中怎么看版本号符号。 版本号符号的解释 版本号通常由三部分组成:主版本号、次版本号、补丁版本号,格式为 major.minor.patch。常见的符号有: ^:更新时允许自动…...
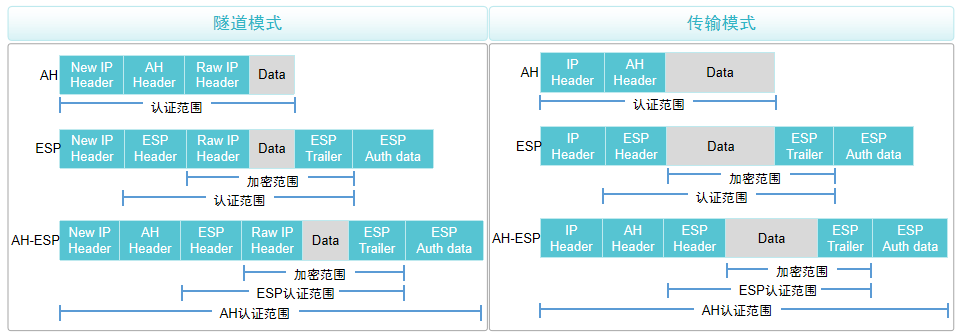
计算机网络-IPSec VPN基本概念
企业分支之间经常有互联的需求,企业互联的方式很多,可以使用专线线路或者Internet线路。部分企业从成本和需求出发会选择使用Internet线路进行互联,但是使用Internet线路存在安全风险,如何保障数据在传输时不会被窃取?…...

VsCode运行Ts文件
1. 生成package.json文件 npm init 2. 生成tsconfig.json文件 tsc --init 3. Vscode运行ts文件 在ts文件点击右键执行Run Code,执行ts文件...

模型 AITDA(吸引、兴趣、信任、渴望、行动)
系列文章 分享 模型,了解更多👉 模型_思维模型目录。吸引、兴趣、信任、渴望、行动 五步曲。 1 模型AITDA的应用 1.1 开源AI智能名片小程序的营销策略 一家企业开发了开源AI智能名片小程序,旨在通过S2B2C模式连接供应商和消费者。该企业采用…...

十、软件设计架构-微服务-服务调用Feign
文章目录 前言一、Feign介绍1. 什么是Feign2. 什么是Http客户端3. Feign 和 OpenFeign 的区别 二、Feign底层原理三、Feign工作原理详解1. 动态代理机制2. 动态代理的创建过程3. 创建详细流程4. FeignClient属性 四、Feign使用1. 常规调用2.日志打印3. 添加Header 前言 服务调…...
电子商务人工智能指南 3/6 - 聊天机器人和客户服务
介绍 81% 的零售业高管表示, AI 至少在其组织中发挥了中等至完全的作用。然而,78% 的受访零售业高管表示,很难跟上不断发展的 AI 格局。 近年来,电子商务团队加快了适应新客户偏好和创造卓越数字购物体验的需求。采用 AI 不再是一…...

【AI模型对比】Kimi与ChatGPT的差距:真实对比它们在六大题型中的全面表现!
文章目录 Moss前沿AI语义理解文学知识数学计算天文学知识物理学知识英语阅读理解详细对比列表总结与建议 Moss前沿AI 【OpenAI】获取OpenAI API Key的多种方式全攻略:从入门到精通,再到详解教程!! 【VScode】VSCode中的智能AI-G…...

spring6:2入门
spring6:2入门 目录 spring6:2入门2.1、环境要求2.2、构建模块2.3、程序开发2.3.1、引入依赖2.3.2、创建java类2.3.3、创建配置文件2.3.4、创建测试类测试2.3.5、运行测试程序 2.4、程序分析2.5、启用Log4j2日志框架2.5.1、Log4j2日志概述2.5.2、引入Log…...

Netty - NIO基础学习
一 简介 1 三大模型是什么? IO三大模型之一,BIO,AIO,还有我们的主角NIO(non-blocking-io),也就是同步非阻塞式IO。这三种模型到底是干什么的?其实这三种模型都是对于JAVA的一种I/O框架,用来进行…...

ArrayList的自动扩容机制源码
Java的ArrayList的自动扩容机制 ArrayList是 Java 中极为常用的动态数组实现类,它依托数组存储数据,能依据实际需求灵活变动容量,高效管理元素集合。在深挖底层源码细节前,先来了解创建ArrayList集合并添加元素时的运作流程&#…...
)
【llm_inference】react框架(最小code实现)
ReAct:结合推理和行动的大语言模型推理架构 GitHub Code: 人人都能看懂的最小实现 引言 在人工智能领域,大语言模型(LLM)的应用日益广泛,但如何让模型能够像人类一样,在思考的基础上采取行动,…...

PT8M2103 触控 I/O 型 8-Bit MCU
1 产品概述 ● PT8M2103 是一款可多次编程(MTP)I/O 型8位 MCU,其包括 2K*16bit MTP ROM、256*8bit SRAM、PWM、Touch 等功能,具有高性能精简指令集、低工作电压、低功耗特性且完全集成触控按键功能。为各种触控按键的应用,提供了一种简单而又…...

英语时态学习+名词副词形容词变形方式
开发出头不容易 不如跨界卷英语 英语中的16种时态是由四种时间(现在、过去、将来、过去将来)和四种体(一般、进行、完成、完成进行)组合而成的。以下是每种时态的详细说明和例句: 一般现在时 (Simple Present) 用法…...

IDEA运行Tomcat出现乱码问题解决汇总
最近正值期末周,有很多同学在写期末Java web作业时,运行tomcat出现乱码问题,经过多次解决与研究,我做了如下整理: 原因: IDEA本身编码与tomcat的编码与Windows编码不同导致,Windows 系统控制台…...

【Web 进阶篇】优雅的接口设计:统一响应、全局异常处理与参数校验
系列回顾: 在上一篇中,我们成功地为应用集成了数据库,并使用 Spring Data JPA 实现了基本的 CRUD API。我们的应用现在能“记忆”数据了!但是,如果你仔细审视那些 API,会发现它们还很“粗糙”:有…...

土地利用/土地覆盖遥感解译与基于CLUE模型未来变化情景预测;从基础到高级,涵盖ArcGIS数据处理、ENVI遥感解译与CLUE模型情景模拟等
🔍 土地利用/土地覆盖数据是生态、环境和气象等诸多领域模型的关键输入参数。通过遥感影像解译技术,可以精准获取历史或当前任何一个区域的土地利用/土地覆盖情况。这些数据不仅能够用于评估区域生态环境的变化趋势,还能有效评价重大生态工程…...

rnn判断string中第一次出现a的下标
# coding:utf8 import torch import torch.nn as nn import numpy as np import random import json""" 基于pytorch的网络编写 实现一个RNN网络完成多分类任务 判断字符 a 第一次出现在字符串中的位置 """class TorchModel(nn.Module):def __in…...

以光量子为例,详解量子获取方式
光量子技术获取量子比特可在室温下进行。该方式有望通过与名为硅光子学(silicon photonics)的光波导(optical waveguide)芯片制造技术和光纤等光通信技术相结合来实现量子计算机。量子力学中,光既是波又是粒子。光子本…...

接口自动化测试:HttpRunner基础
相关文档 HttpRunner V3.x中文文档 HttpRunner 用户指南 使用HttpRunner 3.x实现接口自动化测试 HttpRunner介绍 HttpRunner 是一个开源的 API 测试工具,支持 HTTP(S)/HTTP2/WebSocket/RPC 等网络协议,涵盖接口测试、性能测试、数字体验监测等测试类型…...

Razor编程中@Html的方法使用大全
文章目录 1. 基础HTML辅助方法1.1 Html.ActionLink()1.2 Html.RouteLink()1.3 Html.Display() / Html.DisplayFor()1.4 Html.Editor() / Html.EditorFor()1.5 Html.Label() / Html.LabelFor()1.6 Html.TextBox() / Html.TextBoxFor() 2. 表单相关辅助方法2.1 Html.BeginForm() …...

nnUNet V2修改网络——暴力替换网络为UNet++
更换前,要用nnUNet V2跑通所用数据集,证明nnUNet V2、数据集、运行环境等没有问题 阅读nnU-Net V2 的 U-Net结构,初步了解要修改的网络,知己知彼,修改起来才能游刃有余。 U-Net存在两个局限,一是网络的最佳深度因应用场景而异,这取决于任务的难度和可用于训练的标注数…...

Linux部署私有文件管理系统MinIO
最近需要用到一个文件管理服务,但是又不想花钱,所以就想着自己搭建一个,刚好我们用的一个开源框架已经集成了MinIO,所以就选了这个 我这边对文件服务性能要求不是太高,单机版就可以 安装非常简单,几个命令就…...

用鸿蒙HarmonyOS5实现中国象棋小游戏的过程
下面是一个基于鸿蒙OS (HarmonyOS) 的中国象棋小游戏的实现代码。这个实现使用Java语言和鸿蒙的Ability框架。 1. 项目结构 /src/main/java/com/example/chinesechess/├── MainAbilitySlice.java // 主界面逻辑├── ChessView.java // 游戏视图和逻辑├──…...
