Dijkstra 算法 是什么?
Dijkstra 算法
Dijkstra 算法是一种经典的最短路径算法,用于在图(有向或无向图)中找到从起点到其他所有节点的最短路径。它以广度优先搜索的方式,逐步扩展到目标节点,确保计算出的路径是最短的。
1. Dijkstra 算法的基本概念
特点
- 适用于非负权值的图。
- 能够找到从单一源节点到所有其他节点的最短路径。
输入
- 一个图(节点和边)。
- 起始节点(源节点)。
输出
- 从起始节点到其他所有节点的最短路径长度。
- 如果需要,可以记录路径上的具体节点。
2. 核心思想
Dijkstra 算法的核心思想是:
- 利用贪心策略,每次选择当前未访问的、距离起点最近的节点进行扩展。
- 一旦访问一个节点,其最短路径就不会被更新(路径确定性)。
3. 算法步骤
初始化
- 创建一个距离表(distance table):
- 对每个节点初始化为无穷大(∞),表示当前未知最短路径。
- 起点的距离设为 0:
distance[start] = 0。
- 创建一个访问表(visited set),记录已访问的节点。
- 使用一个优先队列或小顶堆(priority queue)存储待访问节点及其距离。
主循环
- 从优先队列中取出距离起点最近的未访问节点 ( u )。
- 对 ( u ) 的每个邻居节点 ( v ):
- 计算从起点通过 ( u ) 到 ( v ) 的路径距离:
distance[v] = min(distance[v], distance[u] + weight(u, v))。 - 如果路径距离更新了,将 ( v ) 加入优先队列。
- 计算从起点通过 ( u ) 到 ( v ) 的路径距离:
- 将 ( u ) 标记为已访问。
- 重复上述步骤,直到优先队列为空或所有节点的最短路径确定。
路径恢复
如果需要输出路径,可以在更新距离表时记录每个节点的前驱节点,最后从目标节点回溯到起点。
4. 伪代码
Dijkstra(Graph, Start):# 初始化distance = {node: ∞ for node in Graph}distance[Start] = 0visited = set()priority_queue = [(0, Start)] # (distance, node)while priority_queue:# 取出当前距离最小的节点current_distance, current_node = priority_queue.pop()if current_node in visited:continuevisited.add(current_node)# 更新邻居节点的距离for neighbor, weight in Graph[current_node]:new_distance = current_distance + weightif new_distance < distance[neighbor]:distance[neighbor] = new_distancepriority_queue.append((new_distance, neighbor))return distance
5. 示例
图示
假设一个加权图如下:
(A)--1--(B)--4--(D)| |2 2| |(C)--1--(E)
输入
- 起点:
A - 图的权值:
Graph = {A: [(B, 1), (C, 2)], B: [(A, 1), (D, 4), (E, 2)], C: [(A, 2), (E, 1)], ...}
执行步骤
- 初始化:
distance = {A: 0, B: ∞, C: ∞, D: ∞, E: ∞}。 - 选择 ( A ) 开始,更新邻居:
- ( distance[B] = 0 + 1 = 1 )
- ( distance[C] = 0 + 2 = 2 )
- 选择 ( B ):
- ( distance[D] = 1 + 4 = 5 )
- ( distance[E] = 1 + 2 = 3 )
- 选择 ( C ):
- ( distance[E] = min(3, 2 + 1) = 3 )
- 选择 ( E )、( D ),最终得到:
distance = {A: 0, B: 1, C: 2, D: 5, E: 3}。
输出
从 ( A ) 到各节点的最短路径距离:
- ( A \to B: 1 )
- ( A \to C: 2 )
- ( A \to D: 5 )
- ( A \to E: 3 )
6. 优缺点
优点
- 高效:适用于稠密图,时间复杂度为 ( O((V + E) \log V) )(使用堆实现)。
- 稳定:保证找到从起点到各节点的最短路径。
缺点
- 限制:不能处理带负权边的图。
- 局限性:只能从一个起点出发计算最短路径,无法同时处理多源问题。
7. 应用场景
- 导航系统:计算最短路径(如 Google Maps)。
- 网络路由:最优路由规划(如 OSPF 协议)。
- 游戏开发:角色移动规划。
- 交通规划:优化物流路径。
如果需要更详细的代码示例或具体实现,可以进一步探讨!
相关文章:

Dijkstra 算法 是什么?
Dijkstra 算法 Dijkstra 算法是一种经典的最短路径算法,用于在图(有向或无向图)中找到从起点到其他所有节点的最短路径。它以广度优先搜索的方式,逐步扩展到目标节点,确保计算出的路径是最短的。 1. Dijkstra 算法的基…...

英文输入法---华为OD机试2024年E卷
题解: 代码:...

理解 package.json 中版本号符号
今天,聊一聊在前端开发中, package.json 中怎么看版本号符号。 版本号符号的解释 版本号通常由三部分组成:主版本号、次版本号、补丁版本号,格式为 major.minor.patch。常见的符号有: ^:更新时允许自动…...
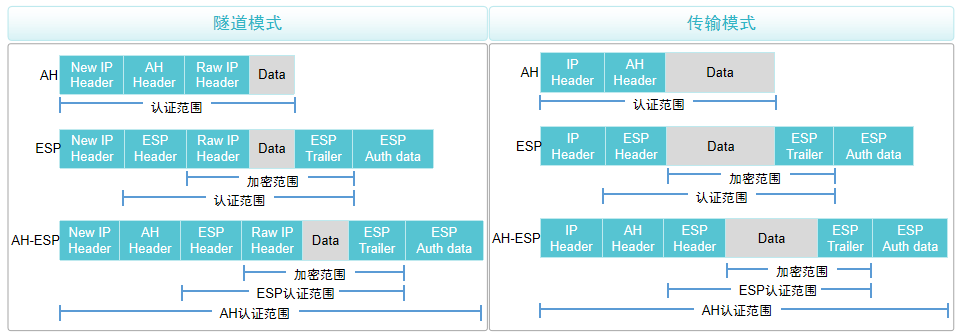
计算机网络-IPSec VPN基本概念
企业分支之间经常有互联的需求,企业互联的方式很多,可以使用专线线路或者Internet线路。部分企业从成本和需求出发会选择使用Internet线路进行互联,但是使用Internet线路存在安全风险,如何保障数据在传输时不会被窃取?…...

VsCode运行Ts文件
1. 生成package.json文件 npm init 2. 生成tsconfig.json文件 tsc --init 3. Vscode运行ts文件 在ts文件点击右键执行Run Code,执行ts文件...

模型 AITDA(吸引、兴趣、信任、渴望、行动)
系列文章 分享 模型,了解更多👉 模型_思维模型目录。吸引、兴趣、信任、渴望、行动 五步曲。 1 模型AITDA的应用 1.1 开源AI智能名片小程序的营销策略 一家企业开发了开源AI智能名片小程序,旨在通过S2B2C模式连接供应商和消费者。该企业采用…...

十、软件设计架构-微服务-服务调用Feign
文章目录 前言一、Feign介绍1. 什么是Feign2. 什么是Http客户端3. Feign 和 OpenFeign 的区别 二、Feign底层原理三、Feign工作原理详解1. 动态代理机制2. 动态代理的创建过程3. 创建详细流程4. FeignClient属性 四、Feign使用1. 常规调用2.日志打印3. 添加Header 前言 服务调…...
电子商务人工智能指南 3/6 - 聊天机器人和客户服务
介绍 81% 的零售业高管表示, AI 至少在其组织中发挥了中等至完全的作用。然而,78% 的受访零售业高管表示,很难跟上不断发展的 AI 格局。 近年来,电子商务团队加快了适应新客户偏好和创造卓越数字购物体验的需求。采用 AI 不再是一…...

【AI模型对比】Kimi与ChatGPT的差距:真实对比它们在六大题型中的全面表现!
文章目录 Moss前沿AI语义理解文学知识数学计算天文学知识物理学知识英语阅读理解详细对比列表总结与建议 Moss前沿AI 【OpenAI】获取OpenAI API Key的多种方式全攻略:从入门到精通,再到详解教程!! 【VScode】VSCode中的智能AI-G…...

spring6:2入门
spring6:2入门 目录 spring6:2入门2.1、环境要求2.2、构建模块2.3、程序开发2.3.1、引入依赖2.3.2、创建java类2.3.3、创建配置文件2.3.4、创建测试类测试2.3.5、运行测试程序 2.4、程序分析2.5、启用Log4j2日志框架2.5.1、Log4j2日志概述2.5.2、引入Log…...

Netty - NIO基础学习
一 简介 1 三大模型是什么? IO三大模型之一,BIO,AIO,还有我们的主角NIO(non-blocking-io),也就是同步非阻塞式IO。这三种模型到底是干什么的?其实这三种模型都是对于JAVA的一种I/O框架,用来进行…...

ArrayList的自动扩容机制源码
Java的ArrayList的自动扩容机制 ArrayList是 Java 中极为常用的动态数组实现类,它依托数组存储数据,能依据实际需求灵活变动容量,高效管理元素集合。在深挖底层源码细节前,先来了解创建ArrayList集合并添加元素时的运作流程&#…...
)
【llm_inference】react框架(最小code实现)
ReAct:结合推理和行动的大语言模型推理架构 GitHub Code: 人人都能看懂的最小实现 引言 在人工智能领域,大语言模型(LLM)的应用日益广泛,但如何让模型能够像人类一样,在思考的基础上采取行动,…...

PT8M2103 触控 I/O 型 8-Bit MCU
1 产品概述 ● PT8M2103 是一款可多次编程(MTP)I/O 型8位 MCU,其包括 2K*16bit MTP ROM、256*8bit SRAM、PWM、Touch 等功能,具有高性能精简指令集、低工作电压、低功耗特性且完全集成触控按键功能。为各种触控按键的应用,提供了一种简单而又…...

英语时态学习+名词副词形容词变形方式
开发出头不容易 不如跨界卷英语 英语中的16种时态是由四种时间(现在、过去、将来、过去将来)和四种体(一般、进行、完成、完成进行)组合而成的。以下是每种时态的详细说明和例句: 一般现在时 (Simple Present) 用法…...

浏览器解析页面流程
从输入一个url到页面解析完成的流程 1. 网络进程 1. 获取url 浏览器首先判断输入的url是否有http缓存,如果有则直接从http缓存中读取数据并显示。如果没有,则进行下一步。进行DNS解析,获取域名对应的IP地址。 2.下载html文件 浏览器根据I…...

图的遍历之DFS邻接矩阵法
本题要求实现一个函数,对给定的用邻接矩阵存储的无向无权图,以及一个顶点的编号v,打印以v为起点的一个深度优先搜索序列。 当搜索路径不唯一时,总是选取编号较小的邻接点。 本题保证输入的数据(顶点数量、起点的编号等…...

Java --- JVM编译运行过程
目录 一.Java编译与执行流程: 二.编译过程: 1.编译器(javac): 2.字节码文件(.class): 三.执行过程: 1.启动JVM(Java虚拟机): 2…...

HTML5 拖拽 API 深度解析
一、HTML5 拖拽 API 深度解析 1.1 背景与发展 HTML5 的拖拽 API 是为了解决传统拖拽操作复杂而设计的。传统方法依赖鼠标事件和复杂的逻辑计算,而 HTML5 提供了标准化的拖拽事件和数据传递机制,使得开发者能够快速实现从一个元素拖拽到另一个元素的交互…...
GO--基于令牌桶和漏桶的限流策略
至于为什么要限流,字面意思已经很清楚了,就是为了减轻服务器的压力 下面我们将介绍两个限流策略----漏桶和令牌桶。 漏桶 原理介绍 漏桶,顾名思义就是一个漏斗,漏斗嘴的大小是固定的,所以不管漏斗现容量多大&#…...

MPNet:旋转机械轻量化故障诊断模型详解python代码复现
目录 一、问题背景与挑战 二、MPNet核心架构 2.1 多分支特征融合模块(MBFM) 2.2 残差注意力金字塔模块(RAPM) 2.2.1 空间金字塔注意力(SPA) 2.2.2 金字塔残差块(PRBlock) 2.3 分类器设计 三、关键技术突破 3.1 多尺度特征融合 3.2 轻量化设计策略 3.3 抗噪声…...

Linux相关概念和易错知识点(42)(TCP的连接管理、可靠性、面临复杂网络的处理)
目录 1.TCP的连接管理机制(1)三次握手①握手过程②对握手过程的理解 (2)四次挥手(3)握手和挥手的触发(4)状态切换①挥手过程中状态的切换②握手过程中状态的切换 2.TCP的可靠性&…...

系统设计 --- MongoDB亿级数据查询优化策略
系统设计 --- MongoDB亿级数据查询分表策略 背景Solution --- 分表 背景 使用audit log实现Audi Trail功能 Audit Trail范围: 六个月数据量: 每秒5-7条audi log,共计7千万 – 1亿条数据需要实现全文检索按照时间倒序因为license问题,不能使用ELK只能使用…...

tomcat指定使用的jdk版本
说明 有时候需要对tomcat配置指定的jdk版本号,此时,我们可以通过以下方式进行配置 设置方式 找到tomcat的bin目录中的setclasspath.bat。如果是linux系统则是setclasspath.sh set JAVA_HOMEC:\Program Files\Java\jdk8 set JRE_HOMEC:\Program Files…...

vue3 daterange正则踩坑
<el-form-item label"空置时间" prop"vacantTime"> <el-date-picker v-model"form.vacantTime" type"daterange" start-placeholder"开始日期" end-placeholder"结束日期" clearable :editable"fal…...

消防一体化安全管控平台:构建消防“一张图”和APP统一管理
在城市的某个角落,一场突如其来的火灾打破了平静。熊熊烈火迅速蔓延,滚滚浓烟弥漫开来,周围群众的生命财产安全受到严重威胁。就在这千钧一发之际,消防救援队伍迅速行动,而豪越科技消防一体化安全管控平台构建的消防“…...

xmind转换为markdown
文章目录 解锁思维导图新姿势:将XMind转为结构化Markdown 一、认识Xmind结构二、核心转换流程详解1.解压XMind文件(ZIP处理)2.解析JSON数据结构3:递归转换树形结构4:Markdown层级生成逻辑 三、完整代码 解锁思维导图新…...

企业大模型服务合规指南:深度解析备案与登记制度
伴随AI技术的爆炸式发展,尤其是大模型(LLM)在各行各业的深度应用和整合,企业利用AI技术提升效率、创新服务的步伐不断加快。无论是像DeepSeek这样的前沿技术提供者,还是积极拥抱AI转型的传统企业,在面向公众…...

Vue 3 + WebSocket 实战:公司通知实时推送功能详解
📢 Vue 3 WebSocket 实战:公司通知实时推送功能详解 📌 收藏 点赞 关注,项目中要用到推送功能时就不怕找不到了! 实时通知是企业系统中常见的功能,比如:管理员发布通知后,所有用户…...

《Offer来了:Java面试核心知识点精讲》大纲
文章目录 一、《Offer来了:Java面试核心知识点精讲》的典型大纲框架Java基础并发编程JVM原理数据库与缓存分布式架构系统设计二、《Offer来了:Java面试核心知识点精讲(原理篇)》技术文章大纲核心主题:Java基础原理与面试高频考点Java虚拟机(JVM)原理Java并发编程原理Jav…...
