【数据结构】哈夫曼树
哈夫曼树
路径长度:从树中一个结点到另一个结点之间的分支构成这两个节点之间的路径,路径上的分支数目称为路径长度
树的带权路径长度:树中所有叶子结点的带权路径长度之和,通常记为WPL= ∑ k = 1 n w k l k \sum^{n}_{k=1}w_kl_k ∑k=1nwklk
带权路径长度最小的二叉树称为最优二叉树或哈夫曼树
注意:
哈夫曼树不一定是完全二叉树
书中一定没有度为1的结点
树中权值最小的两个结点一定是兄弟
包含n个叶子节点的哈夫曼树共有2n-1个结点
包含n棵树的森林要经过n-1次合并才能形成哈夫曼树,共形成n-1个新结点,且度为2
树中任意非叶子节点的权值一定不小于下一层任意结点的权值
哈夫曼树的构造
哈夫曼算法:
- 根据给定的权值构成n棵二叉树的森林,每棵树只有一个带权为wi的根节点
- 在森林中选取两棵根节点权值最小的树作为左右子树,构造一棵新的二叉树,且设置新的二叉树的根节点的权值为其左右子树的权值和
- 在森林中删除这两棵树,同时将新得到的二叉树加入森林中
- 重复(2)(3),直到森林中只有一棵树为止,这棵树即为哈夫曼树(重复第二步时不一定选用新树)
哈夫曼树的实现
采用顺序存储结构
typedef struct{int weight;int parent,lch,rch;
}HTNode,*HTree;
void CreateHuffmanTree(HuffmanTree HT,int n){if(n<=1)return;m=2*n-1;//数组共2n-1个元素HT=new HTNode[m+1];//0号单元未用,HT[m]表示根节点for(i=1;i<=m;i++){ //将2n-1个元素的lch、rch、parent置为0HT[i].lch=0;HT[i].rch=0;HT[i].parent=0;}for(i=1;i<=n;++i)cin>>HT[i].weight;//输入前n个元素的weight值//初始化结束,下面开始建立哈夫曼树for(i=n+1;i<=m;i++){ //合并产生n-1个结点——构造Huffman树Select(HT,i-1,s1,s2);//在HT[k]中选择两个双亲域为0,且权值最小的结点,并返回它们在HT中的序号s1和s2HT[s1].parent=i;HT[s2].parent=i; //表示从F中删除s1、s2HT[i].lch=s1; HT[i].rch=s2; //s1,s2分别作为i的左右孩子HT[i].weight=HT[s1].weight+HT[s2].weight;//i的权值为左右孩子权值之和}
}
哈夫曼编码
将编码设计为不等长的二进制编码,让代传字符中出现次数较多的字符采用较短的编码
前缀编码:任一个字符的编码都不是另一个字符的字符的编码的前缀
构造哈夫曼编码:
- 将字符出现的频率作为权值,构建哈夫曼树
- 从根节点出发,左分支标记0,右分支标记1
- 从根节点出发,到叶子节点,路过的所有分支的编码组合起来,就是哈夫曼编码
相关文章:

【数据结构】哈夫曼树
哈夫曼树 路径长度:从树中一个结点到另一个结点之间的分支构成这两个节点之间的路径,路径上的分支数目称为路径长度 树的带权路径长度:树中所有叶子结点的带权路径长度之和,通常记为WPL ∑ k 1 n w k l k \sum^{n}_{k1}w_kl_k …...
springboot422甘肃旅游服务平台代码-(论文+源码)_kaic
摘 要 使用旧方法对甘肃旅游服务平台的信息进行系统化管理已经不再让人们信赖了,把现在的网络信息技术运用在甘肃旅游服务平台的管理上面可以解决许多信息管理上面的难题,比如处理数据时间很长,数据存在错误不能及时纠正等问题。这次开发的…...

docker中安装minio
1.首先需要搜索可用镜像,当然也可以不用 docker search minio/minio 2.拉取镜像 docker pull minio/minio 3.在本地新建两个文件夹路径 mkdir -p /opt/minio/datamkdir -p /opt/minio/config解释一下,data是文件存储的首路径。config是配置路径&…...

golang实现简单的reids服务2
golang实现redis兼容的redis服务实现redis兼容的redis服务思路 golang实现redis兼容的redis服务 之前做的redis服务是通过tcp封装的自定义协议 原版项目地址:https://github.com/dengjiayue/my-redis.git 那么能不能实现一个redis兼容的redis服务,这样一般的redis包也可以调…...
: Part 67)
跟李笑来学美式俚语(Most Common American Idioms): Part 67
Most Common American Idioms: Part 67 前言 本文是学习李笑来的Most Common American Idioms这本书的学习笔记,自用。 Github仓库链接:https://github.com/xiaolai/most-common-american-idioms 使用方法: 直接下载下来(或者clone到本地…...

QT 中 QDateTime::currentDateTime() 输出格式备查
基础 QDateTime::currentDateTime() //当前的日期和时间。 QDateTime::toString() //以特定的格式输出时间,格式 yyyy: 年份(4位数) MM: 月份(两位数,07表示七月) dd: 日期(两位数,…...

安卓手机怎么轻松转换更新ip网络地址
随着移动互联网的快速发展,IP地址作为网络身份标识的重要性日益凸显。对于安卓手机用户来说,但有时候我们希望能够轻松转更换ip地址,以提高网络安全性或访问特定内容的需要。那么,安卓手机如何更换IP地址呢?本文将为您…...

spring项目添加本地依赖,报java程序包不存在
删除引入程序中的iml文件 重新在当前项目目录下构建项目...

嵌入式硬件-- 元器件焊接
1.锡膏的使用 锡膏要保存在冰箱里。 焊接排线端子;138度的低温锡(锡膏), 第一次使用,直接拿东西挑一点涂在引脚上,不知道多少合适,加热台加热到260左右,放在上面观察锡融化&#…...

物联网入门-Arduino的下载与配置教程(以ESP32为例)-2024
教程介绍 本次教程主要讲述如何下载与配置Arduino,以及开发版对应驱动的下载安装 原文链接:物联网入门-Arduino的下载与配置教程(以ESP32为例)-2024 步骤概述 1:下载Arduino 2:安装Arduino 3:下载安装驱动 4&am…...
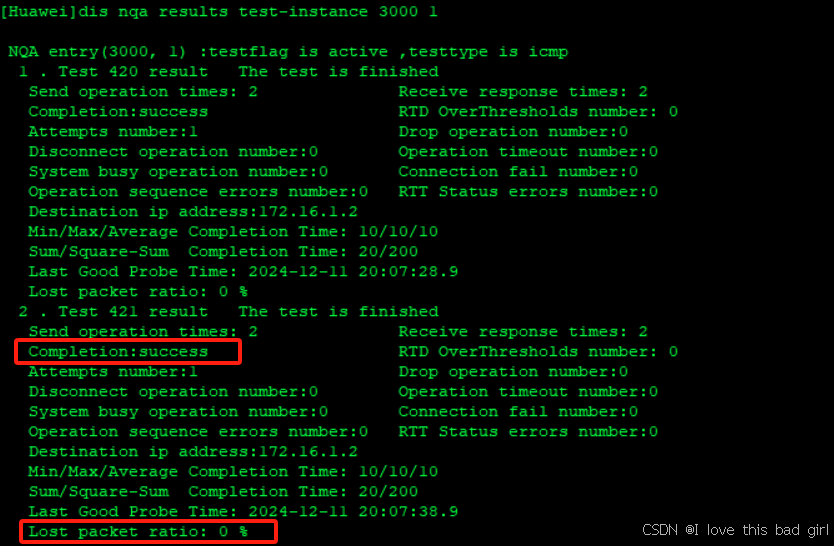
防火墙旁挂部署+故障切换
一、实验环境 华为ENSP 二、拓扑 三、目的 1、内网PC1访问Server 2、防火墙旁挂部署,对流量进行过滤,防火墙挂掉之后,内网PC1能继续访问到Server 3、防火墙恢复正常后,流量能回切至防火墙转发 四、思路: 1、AR1…...

PyTorch基本使用-张量的基本运算及函数计算
文章目录 1. 张量数值计算1. 1 张量基本运算1.2 点乘运算1.3 矩阵运算 2. 张量运算函数 1. 张量数值计算 1. 1 张量基本运算 加减乘除取负号: add、sub、mul、div、neg add_ 、sub_、 mul_ 、div_、 neg_ (其中带下划线的版本会修改原数据) data torch.randin…...
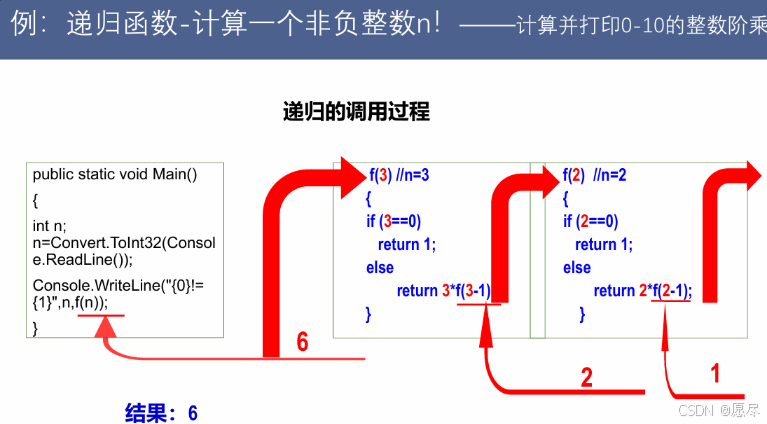
C#--方法
C#的代码包装 三种实现途径:方法、类和名字空间。 • 方法是包含一系列语句的代码块。 • 类用于组合类,方法,属性。 • 将多个相关类组合成名字空间。 静态方法和静态变量 • 静态成员 在类中,使用static修饰符声明的成员称为静态…...

前端权限控制
前端权限控制 一、路由权限(控制页面访问) vue // router.js const routes [{path: /dashboard,name: Dashboard,component: () > import(/views/Dashboard.vue),meta: { requiresAuth: true, roles: [admin, manager] }},{path: /user,name: Use…...

mac下载安装jdk
背景 长时间不折腾mac全部忘记 特此记录 安装 1.下载jdk 根据需要下载对应的jdk 我直接 下载到/Applicatiions目录 https://www.oracle.com/java/technologies/downloads/#java8-mac 2.解压 cd /Applicatiions tar -zxvf jdk-8u431-macosx-x64.tar.gz 3.配置环境 …...
在线PS工具:UI设计的创新选择
对于刚踏入UI设计领域的新手来说,选择合适的在线Photoshop替代工具是至关重要的。市场上存在众多的在线设计工具,让人难以抉择。以下是10个值得尝试的在线PS工具,希望能帮助你找到最适合你的那一款。 Adobe Photoshop Photoshop是设计师们长…...
生成式AI概览与详解
1. 生成式AI概览:什么是大模型,大模型应用场景(文生文,多模态) 生成式AI(Generative AI)是指通过机器学习模型生成新的数据或内容的人工智能技术。生成式AI可以生成文本、图像、音频、视频等多种…...

数据结构与算法学习笔记----树与图的深度优先遍历
数据结构与算法学习笔记----树与图的深度优先遍历 author: 明月清了个风 first publish time: 2024.12.9 pa⭐️这里只有一道题哈哈。 Acwing 846.树的重心 给定一棵树,树中包含 n n n个节点(编号 1 ∼ n 1 \sim n 1∼n)和 n − 1 n - 1 n…...

IEEE T-RO 软体机器人手指状态估计实现两栖触觉传感
摘要:南方科技大学戴建生院士、林间院士、万芳老师、宋超阳老师团队近期在IEEE T-RO上发表了关于软体机器人手指在两栖环境中本体感知方法的论文。 近日,南方科技大学戴建生院士、林间院士、万芳老师、宋超阳老师团队在机器人顶刊IEEE T-RO上以《Propri…...
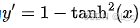
【NLP 14、激活函数 ② tanh激活函数】
学会钝感力,走向美好的方向 —— 24.12.11 一、tanh激活函数 1. tanh函数的定义 tanh是双曲正切函数(Hyperbolic Tangent),数学表达式为 其函数图像是一个S型曲线,以原点 (0,0) 为中心对称,定…...

19c补丁后oracle属主变化,导致不能识别磁盘组
补丁后服务器重启,数据库再次无法启动 ORA01017: invalid username/password; logon denied Oracle 19c 在打上 19.23 或以上补丁版本后,存在与用户组权限相关的问题。具体表现为,Oracle 实例的运行用户(oracle)和集…...

idea大量爆红问题解决
问题描述 在学习和工作中,idea是程序员不可缺少的一个工具,但是突然在有些时候就会出现大量爆红的问题,发现无法跳转,无论是关机重启或者是替换root都无法解决 就是如上所展示的问题,但是程序依然可以启动。 问题解决…...

在鸿蒙HarmonyOS 5中实现抖音风格的点赞功能
下面我将详细介绍如何使用HarmonyOS SDK在HarmonyOS 5中实现类似抖音的点赞功能,包括动画效果、数据同步和交互优化。 1. 基础点赞功能实现 1.1 创建数据模型 // VideoModel.ets export class VideoModel {id: string "";title: string ""…...

《通信之道——从微积分到 5G》读书总结
第1章 绪 论 1.1 这是一本什么样的书 通信技术,说到底就是数学。 那些最基础、最本质的部分。 1.2 什么是通信 通信 发送方 接收方 承载信息的信号 解调出其中承载的信息 信息在发送方那里被加工成信号(调制) 把信息从信号中抽取出来&am…...

如何在最短时间内提升打ctf(web)的水平?
刚刚刷完2遍 bugku 的 web 题,前来答题。 每个人对刷题理解是不同,有的人是看了writeup就等于刷了,有的人是收藏了writeup就等于刷了,有的人是跟着writeup做了一遍就等于刷了,还有的人是独立思考做了一遍就等于刷了。…...

【Linux】自动化构建-Make/Makefile
前言 上文我们讲到了Linux中的编译器gcc/g 【Linux】编译器gcc/g及其库的详细介绍-CSDN博客 本来我们将一个对于编译来说很重要的工具:make/makfile 1.背景 在一个工程中源文件不计其数,其按类型、功能、模块分别放在若干个目录中,mak…...

Ubuntu系统多网卡多相机IP设置方法
目录 1、硬件情况 2、如何设置网卡和相机IP 2.1 万兆网卡连接交换机,交换机再连相机 2.1.1 网卡设置 2.1.2 相机设置 2.3 万兆网卡直连相机 1、硬件情况 2个网卡n个相机 电脑系统信息,系统版本:Ubuntu22.04.5 LTS;内核版本…...
)
LLaMA-Factory 微调 Qwen2-VL 进行人脸情感识别(二)
在上一篇文章中,我们详细介绍了如何使用LLaMA-Factory框架对Qwen2-VL大模型进行微调,以实现人脸情感识别的功能。本篇文章将聚焦于微调完成后,如何调用这个模型进行人脸情感识别的具体代码实现,包括详细的步骤和注释。 模型调用步骤 环境准备:确保安装了必要的Python库。…...

FFmpeg avformat_open_input函数分析
函数内部的总体流程如下: avformat_open_input 精简后的代码如下: int avformat_open_input(AVFormatContext **ps, const char *filename,ff_const59 AVInputFormat *fmt, AVDictionary **options) {AVFormatContext *s *ps;int i, ret 0;AVDictio…...

Java并发编程实战 Day 11:并发设计模式
【Java并发编程实战 Day 11】并发设计模式 开篇 这是"Java并发编程实战"系列的第11天,今天我们聚焦于并发设计模式。并发设计模式是解决多线程环境下常见问题的经典解决方案,它们不仅提供了优雅的设计思路,还能显著提升系统的性能…...
