深入 TCP VJ-Style
接着 TCP 的文化内涵 继续扯一会儿。
自 30 instruction TCP receive 往前追溯,论文 Jacobson88 源自第一次拥塞崩溃,这篇著名文档在同时期的另一个缘起是另一篇考古文献 [Zhang86] Why TCP Timers Don’t Work Well,后面这篇文献提出了 TCP RTO 的缺陷,指出:
- RTO 是兜底,不要依赖改进 RTO 来优化性能,本质上 RTT 是测不准的;
- 过大过小的 RTO 要么造成连接近乎中断,要么加剧拥塞,当性能太差时,就近乎故障了;
- 虽然 RTO 计算有固有缺陷,但还是需要 “更好的” RTO 计算方法,比如启发式。
VJ 创造了很多技巧,这些技巧携带了很多神秘的 magic number,现在看来这些技巧被认为理所当然到微不足道,早已没人过问理由(一句 “调一手好参数”),但在 1988 年却是精彩且轰动的,它决定了后续至今的 TCP 演化风格。在 VJ 看来,这些 magic number 都是有理由的,这些理由多数来自 VJ-Style,概括讲,VJ-Style 即对指令的节约。
看 VJ 如何改进 RTO 计算。VJ 简单将 rtt 的移动指数平均换了一种写法(以下按照原始论文的写法):
a = ( 1 − g ) ⋅ a + g ⋅ m a=(1-g)\cdot a+g\cdot m a=(1−g)⋅a+g⋅m => a = a + g ⋅ ( m − a ) a=a+g\cdot (m-a) a=a+g⋅(m−a)
后面的形式直接就有了 “物理意义”,(m - a) 即误差,这个迭代过程展示的是一个校准过程,rtt 不断收敛到正确的值。
由此 (m - a) 作为一个 “误差” 整体直接参与描述 “方差”。VJ-Style 体现在他没有使用真正的方差 Σ ∣ m − a ∣ 2 \Sigma|m-a|^2 Σ∣m−a∣2,理由是它包含乘法,乘方运算,存在整数溢出的风险, “不太容易计算” 一直是 VJ 的动力,VJ-Style 偏爱简单的整数加减和移位运算。
VJ 采用 m d e v 2 = ( Σ ∣ m − a ∣ ) 2 ≥ Σ ∣ m − a ∣ 2 = s d e v 2 mdev^2=(\Sigma|m-a|)^2\ge\Sigma|m-a|^2=sdev^2 mdev2=(Σ∣m−a∣)2≥Σ∣m−a∣2=sdev2 作为替换,他证明了 mdev 和 sdev 之间存在简单关系,从而确认 mdev 作为 “误差” 的直接表示,恰好是 sdev 一个很好的近似。
接下来表示 mdev 均值的方法与表示 rtt 的方法相同,然后用这个 “误差” 来修正 rtt 本身:
E r r = m − a Err=m-a Err=m−a
a = a + g ⋅ E r r a=a+g\cdot Err a=a+g⋅Err
v = v + g ⋅ ( ∣ E r r ∣ − v ) v=v+g\cdot (|Err|-v) v=v+g⋅(∣Err∣−v)
很精彩!对 srtt 移动指数平均的简单变形直接导出了这个闭环。精彩还在继续。
为了 “快速计算”,消除 <1 的 g 的方式是缩放,用 g = 1 2 n g=\dfrac{1}{2^n} g=2n1 进行缩放可以利用简单的移位运算:
2 n ⋅ a = 2 n ⋅ a + E r r 2^n\cdot a=2^n\cdot a+Err 2n⋅a=2n⋅a+Err
2 n ⋅ v = 2 n ⋅ v + ( ∣ E r r ∣ − v ) 2^n \cdot v=2^n \cdot v+(|Err|-v) 2n⋅v=2n⋅v+(∣Err∣−v)
剩下的事只是选择 n,而 n = 3 时,效果最接近 RFC793 的建议,由此,VJ 完成了对 rtt 计算的一次优化,下面的代码直到现在还在被各种 TCP 实现几乎照抄:
/* 更新平均估计 */
m -= (sa >> 3);
sa += m;
/* 更新偏差估计 */
if (m < 0)m = -m;
m -= (sv >> 3);
sv += m;
Linux 内核的 tcp_rtt_estimator 也在采用。
剩下的计算 RTO 自然水到渠成,它由 rtt 加上 “误差” 的一定增益组成:
R T O = a + 4 ⋅ v RTO=a+4\cdot v RTO=a+4⋅v
这里的 4 来自现实数据统计律,因为它不太小,足够大。仍然是为了便于计算,v 的 g 采用了 1/4:
2 3 ⋅ a = 2 3 ⋅ a + E r r 2^3\cdot a=2^3\cdot a+Err 23⋅a=23⋅a+Err
2 2 ⋅ v = 2 2 ⋅ v + ( ∣ E r r ∣ − v ) 2^2 \cdot v=2^2 \cdot v+(|Err|-v) 22⋅v=22⋅v+(∣Err∣−v)
m -= (sa >> 3);
sa += m;
if (m < 0)m = -m;
m -= (sv >> 2);
sv += m;
rto = (sa >> 3) + sv;
这完美解决了 Lixia Zhang 在 Zhang86 提出的问题,至今工作良好。
RTO 的魔数 4 还来自 VJ 慢启动的理论分析。如果在慢启动轮次结束时计算的重传超时小于等于下一轮的实际 rtt,就会发生虚假重传。最坏情况下,假设所有延迟都由窗口大小的数据排队引发,延迟将每轮翻倍(因为窗口大小翻倍),因此 R i + 1 = 2 ⋅ R i R_{i+1}=2\cdot R_i Ri+1=2⋅Ri,而 V i = R i − R i − 1 = R i 2 V_i=R_i-R_{i-1}=\dfrac{R_i}{2} Vi=Ri−Ri−1=2Ri,所以 R T O i = R i + R i + 4 V i = 3 R i > 2 R i > R i + 1 RTO_i=R_i+R_i+4V_i=3R_i>2R_i>R_{i+1} RTOi=Ri+Ri+4Vi=3Ri>2Ri>Ri+1,因此虚假重传将不会发生,好精彩!
AIMD 的 Additive Increase 过程每个 ACK 导致 w 增加 1 / w,这导致了除法运算,不仅如此,VJ 建议不要发送 MTU 分数倍的数据包,因为这会降低载荷率,二力合一,VJ-Style 的 AIMD 采用计数方式简单避免了除法运算:
snd_cwnd_cnt ++;
if (snd_cwnd_cnt > cwnd)cwnd ++;
先写到这,其余的参考 RFC1072 后面再说。
浙江温州皮鞋湿,下雨进水不会胖。
相关文章:

深入 TCP VJ-Style
接着 TCP 的文化内涵 继续扯一会儿。 自 30 instruction TCP receive 往前追溯,论文 Jacobson88 源自第一次拥塞崩溃,这篇著名文档在同时期的另一个缘起是另一篇考古文献 [Zhang86] Why TCP Timers Don’t Work Well,后面这篇文献提出了 TCP…...

go高性能单机缓存项目
代码 // Copyright 2021 ByteDance Inc. // // Licensed under the Apache License, Version 2.0 (the "License"); // you may not use this file except in compliance with the License. // You may obtain a copy of the License at // // http://www.apach…...

数据结构绪论
文章目录 绪论数据结构三要素算法 🏡作者主页:点击! 🤖数据结构专栏:点击! ⏰️创作时间:2024年12月12日01点09分 绪论 数据是信息的载体,描述客观事物属性的数、字符及所有能输入…...

前端开发常用四大框架学习难度咋样?
前端开发常用四大框架指的是 jQuery vue react angular jQuery: 学习难度:相对较低特点:jQuery 是一个快速、小巧、功能丰富的 JavaScript 库。它使得 HTML 文档遍历和操作、事件处理、动画和 Ajax 交互更加简单。适用场景&a…...

OWASP 十大安全漏洞的原理
1. Broken Access Control(访问控制失效) 原理:应用程序未正确实施权限检查,导致攻击者通过篡改请求、强制浏览或权限提升等手段绕过访问控制。 攻击手段: 修改 URL、HTML、或 API 请求以访问未经授权的资源。 删除…...

论文 | ChunkRAG: Novel LLM-Chunk Filtering Method for RAG Systems
本文详细介绍了一种新颖的检索增强生成(Retrieval-Augmented Generation, RAG)系统方法——ChunkRAG,该方法通过对文档的分块语义分析和过滤显著提升了生成系统的准确性和可靠性。 1. 研究背景与问题 1.1 检索增强生成的意义 RAG系统结合…...

ORACLE SQL思路: 多行数据有相同字段就合并成一条数据 分页展示
数据 分数表: 学号,科目名(A,B,C),分数 需求 分页列表展示, 如果一个学号的科目有相同的分数, 合并成一条数据,用 拼接 科目名 ORACLE SQL 实现 SELECT Z.*, SUBSTR(DECODE(f…...
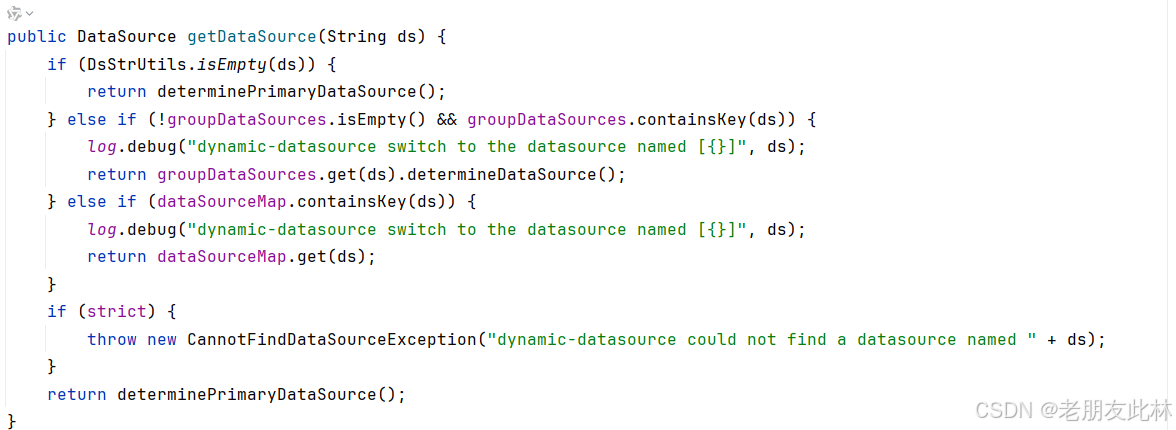
SpringBoot 手动实现动态切换数据源 DynamicSource (中)
大家好,我是此林。 SpringBoot 手动实现动态切换数据源 DynamicSource (上)-CSDN博客 在上一篇博客中,我带大家手动实现了一个简易版的数据源切换实现,方便大家理解数据源切换的原理。今天我们来介绍一个开源的数据源…...
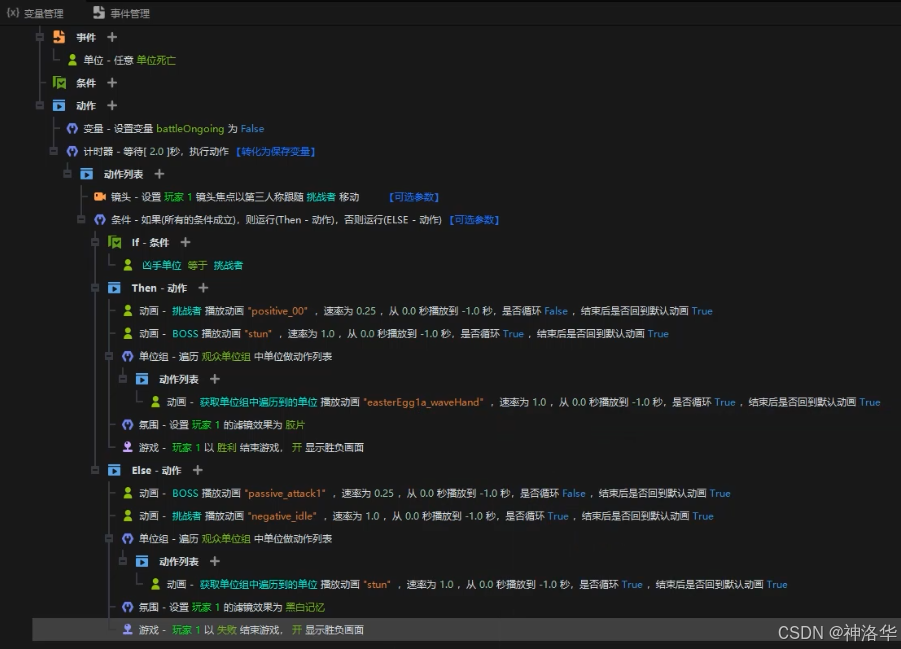
y3编辑器教学5:触发器2 案例演示
文章目录 一、探索1.1 ECA1.1.1 ECA的定义1.1.2 使用触发器实现瞬间移动效果 1.2 变量1.2.1 什么是变量1.2.2 使用变量存储碎片收集数量并展现 1.3 if语句(魔法效果挂接)1.3.1 地形设置1.3.2 编写能量灌注逻辑1.3.3 编写能量灌注后,实现传送逻…...

数值分析——插值法(二)
文章目录 前言一、Hermite插值1.两点三次Hermite插值2.两点三次Hermite插值的推广3.非标准型Hermite插值 二、三次样条插值1.概念2.三弯矩方程 前言 之前写过Lagrange插值与Newton插值法的内容,这里介绍一些其他的插值方法,顺便复习数值分析. 一、Hermi…...
杨振宁大学物理视频中黄色的字,c#写程序去掉
先看一下效果:(还有改进的余地) 写了个程序消除杨振宁大学物理中黄色的字 我的方法是笨方法,也比较刻板。 1,首先想到,把屏幕打印下来。c#提供了这样一个函数: Bitmap bmp new Bitmap(640, 48…...

uni-app 设置缓存过期时间【跨端开发系列】
🔗 uniapp 跨端开发系列文章:🎀🎀🎀 uni-app 组成和跨端原理 【跨端开发系列】 uni-app 各端差异注意事项 【跨端开发系列】uni-app 离线本地存储方案 【跨端开发系列】uni-app UI库、框架、组件选型指南 【跨端开…...

微信小程序base64图片与临时路径互相转换
1、base64图片转临时路径 /*** 将base64图片转临时路径* param {*} dataurl* param {*} filename* returns*/base64ImgToFile(dataurl, filename "file") {const base64 dataurl; // base64码const time new Date().getTime();const imgPath wx.env.USER_DATA_P…...

蓝桥杯刷题——day2
蓝桥杯刷题——day2 题目一题干题目解析代码 题目二题干解题思路代码 题目一 题干 三步问题。有个小孩正在上楼梯,楼梯有n阶台阶,小孩一次可以上1阶、2阶或3阶。实现一种方法,计算小孩有多少种上楼梯的方式。结果可能很大,你需要…...

5.删除链表的倒数第N个节点
19.删除链表的倒数第N个节点 题目: 19. 删除链表的倒数第 N 个结点 - 力扣(LeetCode) 分析: 要删除倒数第几个节点,那么我们需要怎么做呢?我们需要定义两个指针,快指针和慢指针,…...

自己总结:selenium高阶知识
全篇大概10000字(含代码),建议阅读时间30min 一、等待机制 如果有一些内容是通过Ajax加载的内容,那就需要等待内容加载完毕才能进行下一步操作。 为了避免人为操作等待,会遇到的问题, selenium将等待转换…...
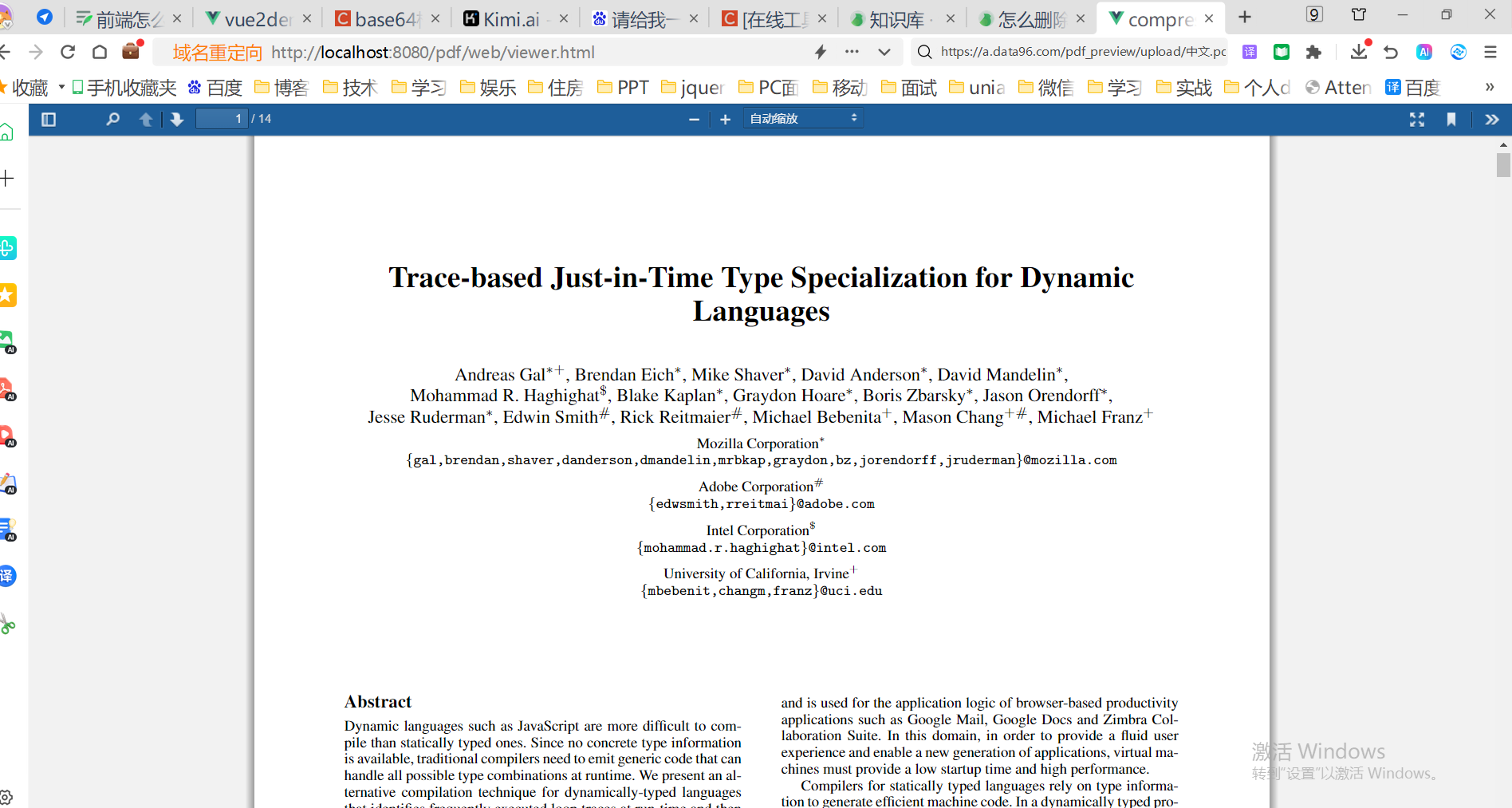
前端怎么预览pdf
1.背景 后台返回了一个在线的pdf地址,需要我这边去做一个pdf的预览(需求1),并且支持配置是否可以下载(需求2),需要在当前页就能预览(需求3)。之前我写过一篇预览pdf的文…...

activemq 的安装部署
下载 https://activemq.apache.org/components/classic/download/# 在/opt目录下载 wget https://dlcdn.apache.org//activemq/5.18.6/apache-activemq-5.18.6-bin.tar.gz解压 tar -zxvf apache-activemq-5.18.6-bin.tar.gz配置java环境 vim /opt/apache-activemq-5.18.6/b…...
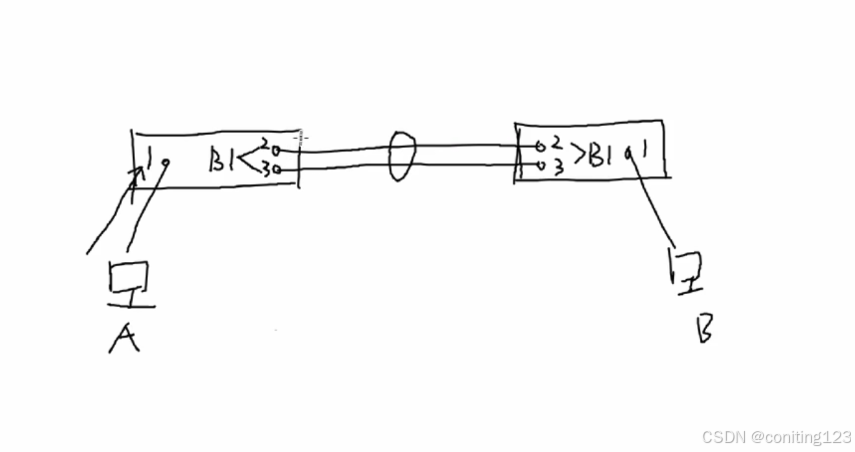
【H3CNE邓方鸣】配置链路聚合+2024.12.11
文章目录 链路聚合作用负载分担分类静态聚合动态聚合 链路聚合作用 定义:把连接到统一交换机上的多个物理端口捆绑为一个逻辑端口 增加链路带宽:聚合组内只要还有物理端口存活,链路就不会中断 提供链路可靠性:避免了STP计算&…...

C语言 学习 日志 递归函数 2024/12/12
C语言 学习 日志 递归函数 介绍: 初始调用:递归函数被首次调用。递归调用:递归函数在其定义中调用自身,创建新的栈帧。基本情况检查:每次递归调用时,检查是否满足基本情况。如果满足,返回结果并开始回溯。…...

谷歌浏览器插件
项目中有时候会用到插件 sync-cookie-extension1.0.0:开发环境同步测试 cookie 至 localhost,便于本地请求服务携带 cookie 参考地址:https://juejin.cn/post/7139354571712757767 里面有源码下载下来,加在到扩展即可使用FeHelp…...

51c自动驾驶~合集58
我自己的原文哦~ https://blog.51cto.com/whaosoft/13967107 #CCA-Attention 全局池化局部保留,CCA-Attention为LLM长文本建模带来突破性进展 琶洲实验室、华南理工大学联合推出关键上下文感知注意力机制(CCA-Attention),…...

遍历 Map 类型集合的方法汇总
1 方法一 先用方法 keySet() 获取集合中的所有键。再通过 gey(key) 方法用对应键获取值 import java.util.HashMap; import java.util.Set;public class Test {public static void main(String[] args) {HashMap hashMap new HashMap();hashMap.put("语文",99);has…...

关于iview组件中使用 table , 绑定序号分页后序号从1开始的解决方案
问题描述:iview使用table 中type: "index",分页之后 ,索引还是从1开始,试过绑定后台返回数据的id, 这种方法可行,就是后台返回数据的每个页面id都不完全是按照从1开始的升序,因此百度了下,找到了…...

前端开发面试题总结-JavaScript篇(一)
文章目录 JavaScript高频问答一、作用域与闭包1.什么是闭包(Closure)?闭包有什么应用场景和潜在问题?2.解释 JavaScript 的作用域链(Scope Chain) 二、原型与继承3.原型链是什么?如何实现继承&a…...

【分享】推荐一些办公小工具
1、PDF 在线转换 https://smallpdf.com/cn/pdf-tools 推荐理由:大部分的转换软件需要收费,要么功能不齐全,而开会员又用不了几次浪费钱,借用别人的又不安全。 这个网站它不需要登录或下载安装。而且提供的免费功能就能满足日常…...

【MATLAB代码】基于最大相关熵准则(MCC)的三维鲁棒卡尔曼滤波算法(MCC-KF),附源代码|订阅专栏后可直接查看
文章所述的代码实现了基于最大相关熵准则(MCC)的三维鲁棒卡尔曼滤波算法(MCC-KF),针对传感器观测数据中存在的脉冲型异常噪声问题,通过非线性加权机制提升滤波器的抗干扰能力。代码通过对比传统KF与MCC-KF在含异常值场景下的表现,验证了后者在状态估计鲁棒性方面的显著优…...

2.3 物理层设备
在这个视频中,我们要学习工作在物理层的两种网络设备,分别是中继器和集线器。首先来看中继器。在计算机网络中两个节点之间,需要通过物理传输媒体或者说物理传输介质进行连接。像同轴电缆、双绞线就是典型的传输介质,假设A节点要给…...

【51单片机】4. 模块化编程与LCD1602Debug
1. 什么是模块化编程 传统编程会将所有函数放在main.c中,如果使用的模块多,一个文件内会有很多代码,不利于组织和管理 模块化编程则是将各个模块的代码放在不同的.c文件里,在.h文件里提供外部可调用函数声明,其他.c文…...

轻量级Docker管理工具Docker Switchboard
简介 什么是 Docker Switchboard ? Docker Switchboard 是一个轻量级的 Web 应用程序,用于管理 Docker 容器。它提供了一个干净、用户友好的界面来启动、停止和监控主机上运行的容器,使其成为本地开发、家庭实验室或小型服务器设置的理想选择…...
