Signature
Signature
题目是:
import ecdsaimport randomdef ecdsa_test(dA,k):sk = ecdsa.SigningKey.from_secret_exponent(secexp=dA,curve=ecdsa.SECP256k1)sig1 = sk.sign(data=b'Hi.', k=k).hex()sig2 = sk.sign(data=b'hello.', k=k).hex()#不同的kr1 = int(sig1[:64], 16)s1 = int(sig1[64:], 16)s2 = int(sig2[64:], 16)return r1,s1,s2if __name__ == '__main__':n = 0xfffffffffffffffffffffffffffffffebaaedce6af48a03bbfd25e8cd0364141a = random.randint(0,n)flag = 'flag{' + str(a) + "}"b = random.randint(0,n)print(ecdsa_test(a,b))# (4690192503304946823926998585663150874421527890534303129755098666293734606680, 111157363347893999914897601390136910031659525525419989250638426589503279490788, 74486305819584508240056247318325239805160339288252987178597122489325719901254)分析代码可以看出,存在随机数重复使用。
具体来说,这段代码中签名的过程中使用了相同的随机数 k 来对不同的消息进行签名。
这种情况下,可以通过分析两个相同 k 值对应的消息签名来恢复私钥 dA。
import sympyfrom hashlib import sha1from Cryptodome.Util.number import long_to_bytes , bytes_to_longdef calculate_private_key(r1, s1, s2, h1, h2, n):# 计算k值k = ((h1 - h2) * sympy.mod_inverse(s1 - s2, n)) % n# 计算私钥dAdA = (sympy.mod_inverse(r1, n) * (k * s1 - h1)) % nreturn dAif __name__ == "__main__":# 定义椭圆曲线的参数n = 0xfffffffffffffffffffffffffffffffebaaedce6af48a03bbfd25e8cd0364141# 签名中的r1, s1, s2值r1 = 4690192503304946823926998585663150874421527890534303129755098666293734606680s1 = 111157363347893999914897601390136910031659525525419989250638426589503279490788s2 = 74486305819584508240056247318325239805160339288252987178597122489325719901254h1 = bytes_to_long(sha1(b'Hi.').digest())h2 = bytes_to_long(sha1(b'hello.').digest())private_key = calculate_private_key(r1, s1, s2, h1, h2, n)print(f'flag{{{private_key}}}')---------------------------------------------------------flag{40355055231406097504270940121798355439363616832290875140843417522164091270174} 椭圆曲线数字签名算法(Elliptic Curve Digital Signature Algorithm,ECDSA)是一种基于椭圆曲线密码学的数字签名算法。它广泛应用于需要确保数据完整性和身份验证的场景中,例如在区块链技术(如比特币)、安全通信协议(如TLS/SSL)等领域。
-
基本原理
ECDSA 是一种非对称加密算法,它基于椭圆曲线数学的复杂性来实现数字签名的生成和验证。其核心思想是利用椭圆曲线上的点的加法运算和标量乘法运算,这些运算在数学上是单向的,即很容易进行正向计算,但很难进行逆向求解。
-
椭圆曲线:椭圆曲线是一种特殊的数学曲线。椭圆曲线上的点具有特殊的代数结构,使得点的加法和标量乘法运算可以高效地实现。
-
私钥和公钥:在 ECDSA 中,私钥是一个随机生成的大整数 d,公钥是椭圆曲线上的一个点 Q,通过 Q=d×G 计算得到,其中 G是椭圆曲线上的一个基点。
-
签名生成过程
签名生成过程主要包括以下步骤:
-
选择随机数:签名者选择一个随机整数 k(称为临时私钥),并计算椭圆曲线上的点 R=k×G。
-
计算 r 和 s:
-
r 是点 R 的 x 坐标对模数 n(椭圆曲线的阶)取模的结果。
-
s=k−1(H(m)+d⋅r)mod n,其中 H(m) 是消息 m 的哈希值,k−1 是 k 的模逆元。
-
-
输出签名:签名由 (r,s) 组成。
-
签名验证过程
验证签名的过程主要包括以下步骤:
-
计算 w:验证者计算 w=s−1mod n。
-
计算 u1 和 u2:
-
u1=H(m)⋅w mod n
-
u2=r⋅w mod n
-
-
计算点 R′:计算 R′=u1×G+u2×Q。
-
验证 r:检查 r 是否等于 R′ 的 x 坐标对模数 n 取模的结果。如果相等,则签名验证通过,否则验证失败。
相关文章:

Signature
Signature 题目是: import ecdsaimport randomdef ecdsa_test(dA,k):sk ecdsa.SigningKey.from_secret_exponent(secexpdA,curveecdsa.SECP256k1)sig1 sk.sign(databHi., kk).hex()sig2 sk.sign(databhello., kk).hex()#不同的kr1 int(sig1[:64], 16)s1 i…...

93,【1】buuctf web [网鼎杯 2020 朱雀组]phpweb
进入靶场 页面一直在刷新 在 PHP 中,date() 函数是一个非常常用的处理日期和时间的函数,所以应该用到了 再看看警告的那句话 Warning: date(): It is not safe to rely on the systems timezone settings. You are *required* to use the date.timez…...
笔灵ai写作技术浅析(四):知识图谱
知识图谱(Knowledge Graph)是一种结构化的知识表示方式,通过将知识以图的形式进行组织,帮助AI系统更好地理解和利用信息。在笔灵AI写作中,知识图谱技术被广泛应用于结构化组织各种领域的知识,使AI能够根据写作主题快速获取相关的背景知识、概念关系等,从而为生成内容提供…...
Chromium132 编译指南 - Android 篇(四):配置 depot_tools
1. 引言 在前面的章节中,我们详细介绍了编译 Chromium 132 for Android 所需的系统和硬件要求,以及如何安装和配置基础开发环境和常用工具。完成这些步骤后,接下来需要配置 depot_tools,这是编译 Chromium 的关键工具集。depot_t…...

使用真实 Elasticsearch 进行高级集成测试
作者:来自 Elastic Piotr Przybyl 掌握高级 Elasticsearch 集成测试:更快、更智能、更优化。 在上一篇关于集成测试的文章中,我们介绍了如何通过改变数据初始化策略来缩短依赖于真实 Elasticsearch 的集成测试的执行时间。在本期中࿰…...

SQL进阶实战技巧:如何分析浏览到下单各步骤转化率及流失用户数?
目录 0 问题描述 1 数据准备 2 问题分析 3 问题拓展 3.1 跳出率计算...
机器学习--概览
一、机器学习基础概念 1. 定义 机器学习(Machine Learning, ML):通过算法让计算机从数据中自动学习规律,并利用学习到的模型进行预测或决策,而无需显式编程。 2. 与编程的区别 传统编程机器学习输入:规…...

低代码系统-产品架构案例介绍、炎黄盈动-易鲸云(十二)
易鲸云作为炎黄盈动新推出的产品,在定位上为低零代码产品。 开发层 表单引擎 表单设计器,包括设计和渲染 流程引擎 流程设计,包括设计和渲染,需要说明的是:采用国际标准BPMN2.0,可以全球通用 视图引擎 视图…...
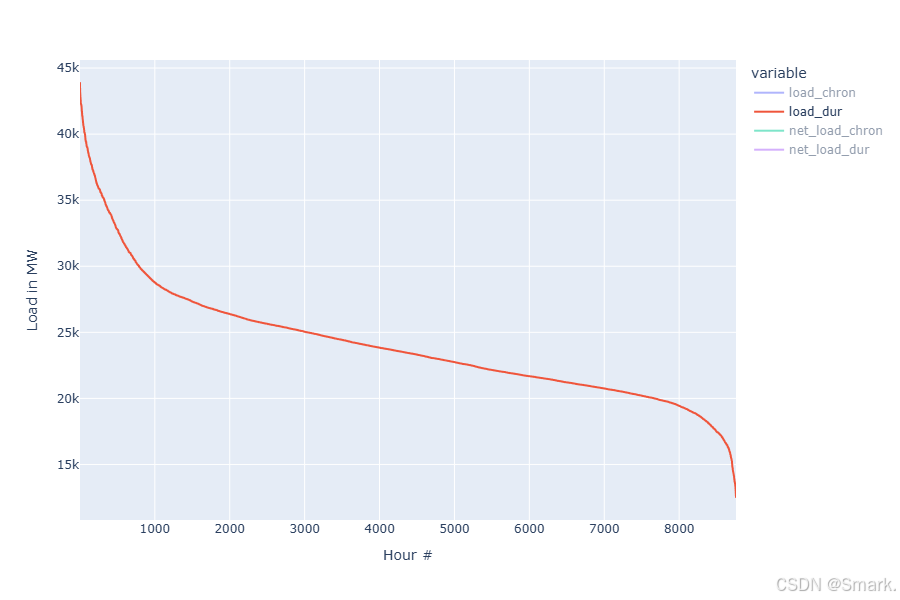
Electricity Market Optimization 探索系列(二)
本文参考链接link 负荷持续时间曲线 (Load Duration Curve),是根据实际的符合数据进行降序排序之后得到的一个曲线 这个曲线能够发现负荷在某个区间时,将会持续多长时间,有助于发电容量的规划 净负荷(net load) 是指预期负荷和预期可再生…...

OpenAI 实战进阶教程 - 第一节:OpenAI API 架构与基础调用
目标 掌握 OpenAI API 的基础调用方法。理解如何通过 API 进行内容生成。使用实际应用场景帮助零基础读者理解 API 的基本用法。 一、什么是 OpenAI API? OpenAI API 是一种工具,允许开发者通过编程方式与 OpenAI 的强大语言模型(例如 gpt-…...
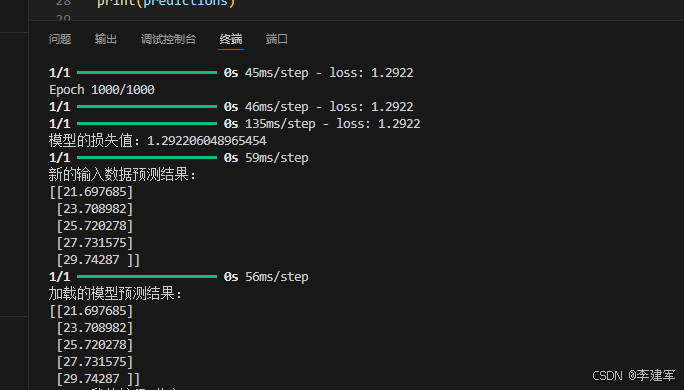
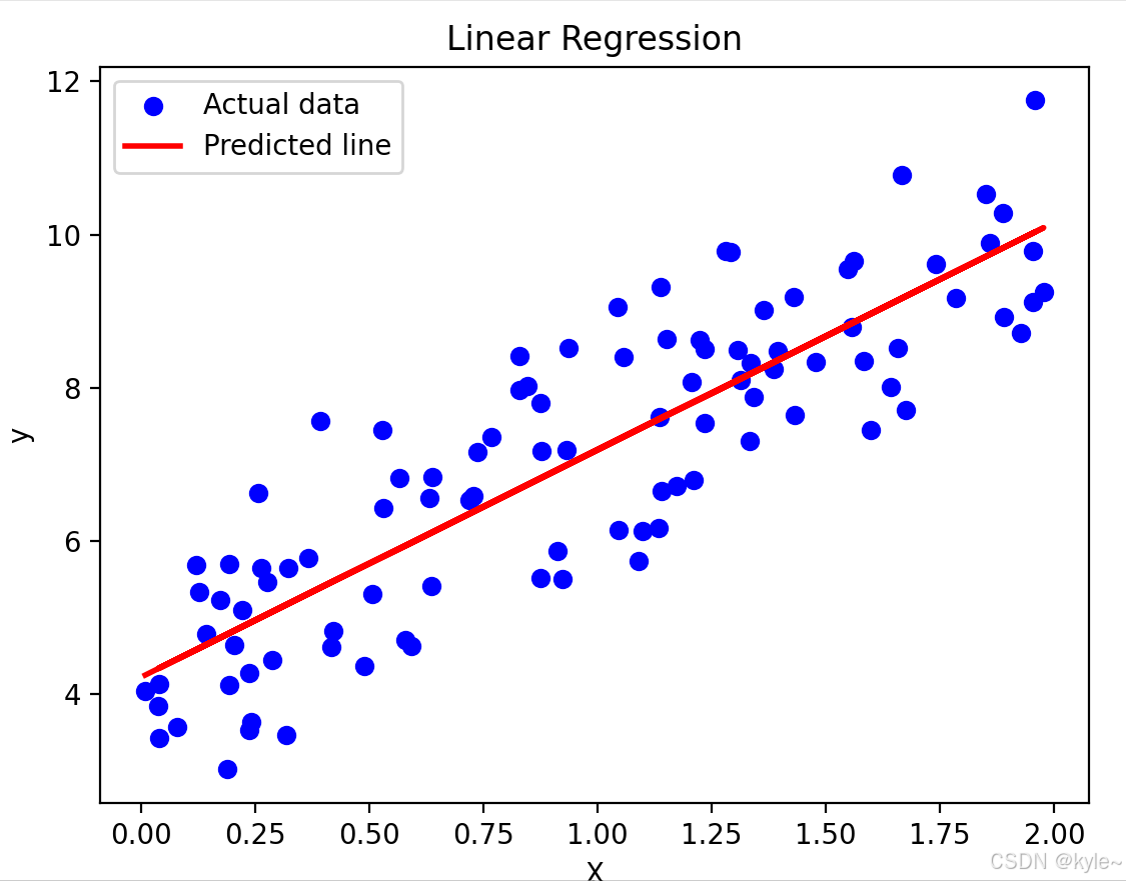
TensorFlow简单的线性回归任务
如何使用 TensorFlow 和 Keras 创建、训练并进行预测 1. 数据准备与预处理 2. 构建模型 3. 编译模型 4. 训练模型 5. 评估模型 6. 模型应用与预测 7. 保存与加载模型 8.完整代码 1. 数据准备与预处理 我们将使用一个简单的线性回归问题,其中输入特征 x 和标…...

【视频+图文详解】HTML基础4-html标签的基本使用
图文教程 html标签的基本使用 无序列表 作用:定义一个没有顺序的列表结构 由两个标签组成:<ul>以及<li>(两个标签都属于容器级标签,其中ul只能嵌套li标签,但li标签能嵌套任何标签,甚至ul标…...

在Arm芯片苹果Mac系统上通过homebrew安装多版本mysql并解决各种报错,感谢deepseek帮助解决部分问题
背景: 1.苹果设备上安装mysql,随着苹果芯片的推出,很多地方都变得不一样了。 2.很多时候为了老项目能运行,我们需要能安装mysql5.7或者mysql8.0或者mysql8.2.虽然本文编写时最新的默认mysql已经是9.2版本。 安装步骤 1.执行hom…...

c++可变参数详解
目录 引言 库的基本功能 va_start 宏: va_arg 宏 va_end 宏 va_copy 宏 使用 处理可变参数代码 C11可变参数模板 基本概念 sizeof... 运算符 包扩展 引言 在C编程中,处理不确定数量的参数是一个常见的需求。为了支持这种需求,C标准库提供了 &…...
【深度分析】DeepSeek 遭暴力破解,攻击 IP 均来自美国,造成影响有多大?有哪些好的防御措施?
技术铁幕下的暗战:当算力博弈演变为代码战争 一场针对中国AI独角兽的全球首例国家级密码爆破,揭开了数字时代技术博弈的残酷真相。DeepSeek服务器日志中持续跳动的美国IP地址,不仅是网络攻击的地理坐标,更是技术霸权对新兴挑战者的…...
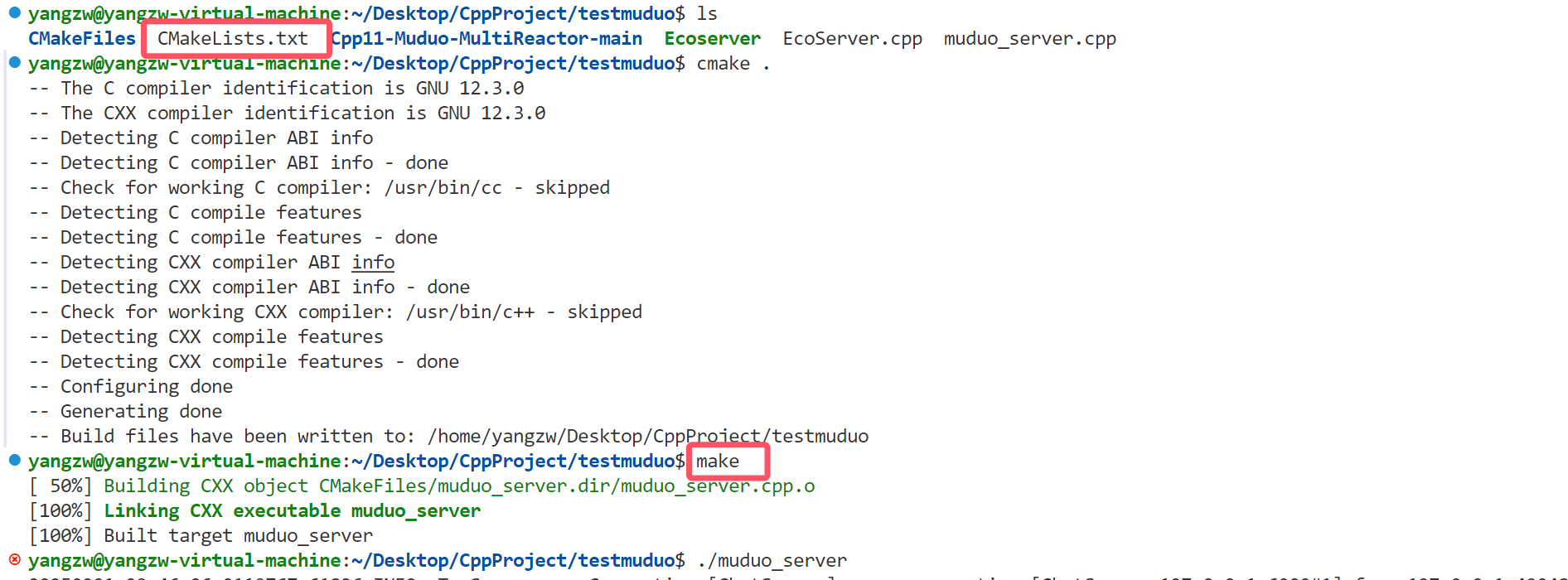
CMake项目编译与开源项目目录结构
Cmake 使用简单方便,可以跨平台构建项目编译环境,尤其比直接写makefile简单,可以通过简单的Cmake生成负责的Makefile文件。 如果没有使用cmake进行编译,需要如下命令:(以muduo库echo服务器为例)…...

完全卸载mysql server步骤
1. 在控制面板中卸载mysql 2. 打开注册表,运行regedit, 删除mysql信息 HKEY_LOCAL_MACHINE-> SYSTEM->CurrentContolSet->Services->EventLog->Application->Mysql HKEY_LOCAL_MACHINE-> SYSTEM->CurrentContolSet->Services->Mysql …...
)
C#方法(练习)
1.定义一个函数,输入三个值,找出三个数中的最小值 2.定义一个函数,输入三个值,找出三个数中的最大值 3.定义一个函数,输入三个值,找出三个数中的平均值 4.定义一个函数,计算一个数的 N 次方 Pow(2, 3)返回8 5.传入十一…...
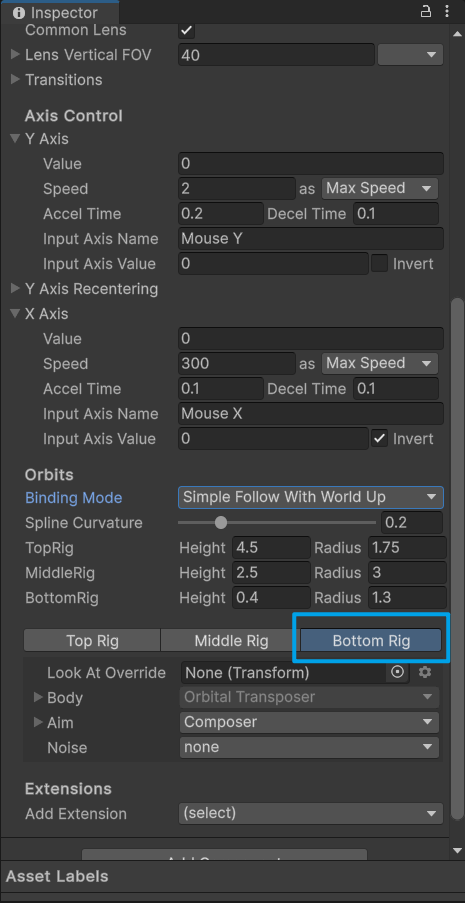
Unity游戏(Assault空对地打击)开发(3) 摄像机的控制
详细步骤 打开My Assets或者Package Manager。 选择Unity Registry。 搜索Cinemachine,找到 Cinemachine包,点击 Install按钮进行安装。 关闭窗口,新建一个FreeLook Camera,如下。 接着新建一个对象Pos,拖到Player下面…...

ChatGPT-4o和ChatGPT-4o mini的差异点
在人工智能领域,OpenAI再次引领创新潮流,近日正式发布了其最新模型——ChatGPT-4o及其经济实惠的小型版本ChatGPT-4o Mini。这两款模型虽同属于ChatGPT系列,但在性能、应用场景及成本上展现出显著的差异。本文将通过图文并茂的方式࿰…...

Mybatis逆向工程,动态创建实体类、条件扩展类、Mapper接口、Mapper.xml映射文件
今天呢,博主的学习进度也是步入了Java Mybatis 框架,目前正在逐步杨帆旗航。 那么接下来就给大家出一期有关 Mybatis 逆向工程的教学,希望能对大家有所帮助,也特别欢迎大家指点不足之处,小生很乐意接受正确的建议&…...

在四层代理中还原真实客户端ngx_stream_realip_module
一、模块原理与价值 PROXY Protocol 回溯 第三方负载均衡(如 HAProxy、AWS NLB、阿里 SLB)发起上游连接时,将真实客户端 IP/Port 写入 PROXY Protocol v1/v2 头。Stream 层接收到头部后,ngx_stream_realip_module 从中提取原始信息…...

OkHttp 中实现断点续传 demo
在 OkHttp 中实现断点续传主要通过以下步骤完成,核心是利用 HTTP 协议的 Range 请求头指定下载范围: 实现原理 Range 请求头:向服务器请求文件的特定字节范围(如 Range: bytes1024-) 本地文件记录:保存已…...

如何将联系人从 iPhone 转移到 Android
从 iPhone 换到 Android 手机时,你可能需要保留重要的数据,例如通讯录。好在,将通讯录从 iPhone 转移到 Android 手机非常简单,你可以从本文中学习 6 种可靠的方法,确保随时保持连接,不错过任何信息。 第 1…...

Python爬虫(一):爬虫伪装
一、网站防爬机制概述 在当今互联网环境中,具有一定规模或盈利性质的网站几乎都实施了各种防爬措施。这些措施主要分为两大类: 身份验证机制:直接将未经授权的爬虫阻挡在外反爬技术体系:通过各种技术手段增加爬虫获取数据的难度…...

UR 协作机器人「三剑客」:精密轻量担当(UR7e)、全能协作主力(UR12e)、重型任务专家(UR15)
UR协作机器人正以其卓越性能在现代制造业自动化中扮演重要角色。UR7e、UR12e和UR15通过创新技术和精准设计满足了不同行业的多样化需求。其中,UR15以其速度、精度及人工智能准备能力成为自动化领域的重要突破。UR7e和UR12e则在负载规格和市场定位上不断优化…...

大学生职业发展与就业创业指导教学评价
这里是引用 作为软工2203/2204班的学生,我们非常感谢您在《大学生职业发展与就业创业指导》课程中的悉心教导。这门课程对我们即将面临实习和就业的工科学生来说至关重要,而您认真负责的教学态度,让课程的每一部分都充满了实用价值。 尤其让我…...

算法笔记2
1.字符串拼接最好用StringBuilder,不用String 2.创建List<>类型的数组并创建内存 List arr[] new ArrayList[26]; Arrays.setAll(arr, i -> new ArrayList<>()); 3.去掉首尾空格...

LeetCode - 199. 二叉树的右视图
题目 199. 二叉树的右视图 - 力扣(LeetCode) 思路 右视图是指从树的右侧看,对于每一层,只能看到该层最右边的节点。实现思路是: 使用深度优先搜索(DFS)按照"根-右-左"的顺序遍历树记录每个节点的深度对于…...
)
C#学习第29天:表达式树(Expression Trees)
目录 什么是表达式树? 核心概念 1.表达式树的构建 2. 表达式树与Lambda表达式 3.解析和访问表达式树 4.动态条件查询 表达式树的优势 1.动态构建查询 2.LINQ 提供程序支持: 3.性能优化 4.元数据处理 5.代码转换和重写 适用场景 代码复杂性…...
