100.1 AI量化面试题:解释夏普比率(Sharpe Ratio)的计算方法及其在投资组合管理中的应用,并说明其局限性
目录
- 0. 承前
- 1. 夏普比率的基本概念
- 1.1 定义与计算方法
- 1.2 实际计算示例
- 2. 在投资组合管理中的应用
- 2.1 投资组合选择
- 2.2 投资组合优化
- 3. 夏普比率的局限性
- 3.1 统计假设的限制
- 3.2 实践中的问题
- 4. 改进方案
- 4.1 替代指标
- 4.2 实践建议
- 5. 回答话术
0. 承前
如果想更加全面清晰地了解金融资产组合模型进化论的体系架构,可参考:
0. 金融资产组合模型进化全图鉴
1. 夏普比率的基本概念
1.1 定义与计算方法
夏普比率是由诺贝尔经济学奖获得者威廉·夏普(William Sharpe)提出的,用于衡量投资组合的风险调整后收益的指标。其计算公式为:
Sharpe Ratio = (Rp - Rf) / σp其中:
Rp = 投资组合的预期收益率
Rf = 无风险利率
σp = 投资组合收益率的标准差
举例来说,假设:
- 某投资组合年化收益率为15%
- 无风险利率为3%
- 标准差为10%
则夏普比率 = (15% - 3%) / 10% = 1.2
1.2 实际计算示例
让我们看一个Python代码示例:
import numpy as np
import pandas as pddef calculate_sharpe_ratio(returns, risk_free_rate):# 计算年化收益率portfolio_return = returns.mean() * 252 # 假设252个交易日# 计算年化波动率portfolio_std = returns.std() * np.sqrt(252)# 计算夏普比率sharpe_ratio = (portfolio_return - risk_free_rate) / portfolio_stdreturn sharpe_ratio# 示例数据
daily_returns = pd.Series([0.001, -0.002, 0.003, -0.001, 0.002]) # 日收益率
risk_free_rate = 0.03 # 年化无风险利率sharpe = calculate_sharpe_ratio(daily_returns, risk_free_rate)
2. 在投资组合管理中的应用
2.1 投资组合选择
夏普比率在投资组合管理中主要用于:
- 比较不同投资组合的表现
- 优化资产配置
- 评估投资经理的业绩
例如,考虑两个投资组合:
- 组合A:年化收益率12%,波动率8%,无风险利率3%
- 组合B:年化收益率18%,波动率15%,无风险利率3%
# 计算结果
夏普比率A = (12% - 3%) / 8% = 1.125
夏普比率B = (18% - 3%) / 15% = 1.000
尽管组合B的绝对收益更高,但从风险调整后的角度来看,组合A的表现更好。
2.2 投资组合优化
在实际应用中,我们经常使用夏普比率来优化投资组合权重:
from scipy.optimize import minimizedef optimize_portfolio(returns, risk_free_rate):def objective(weights):portfolio_return = np.sum(returns.mean() * weights) * 252portfolio_std = np.sqrt(np.dot(weights.T, np.dot(returns.cov() * 252, weights)))sharpe = (portfolio_return - risk_free_rate) / portfolio_stdreturn -sharpe # 最小化的是负夏普比率# 优化过程...return optimal_weights
3. 夏普比率的局限性
3.1 统计假设的限制
-
正态分布假设:夏普比率假设收益率服从正态分布,但实际市场收益往往呈现出偏态和尾部风险。
-
时间依赖性:收益率的均值和标准差可能随时间变化,而夏普比率假设这些参数是稳定的。
3.2 实践中的问题
-
对称性问题:
- 夏普比率对正负波动的处理是对称的
- 但投资者通常更关心下行风险
-
时间周期敏感性:
- 不同计算周期可能得到显著不同的结果
- 例如,日度数据和月度数据计算的夏普比率可能差异较大
-
样本依赖性:
# 示例:不同样本期间的夏普比率差异
sharpe_2019 = calculate_sharpe_ratio(returns_2019, rf_2019)
sharpe_2020 = calculate_sharpe_ratio(returns_2020, rf_2020)
# 可能得到显著不同的结果
4. 改进方案
4.1 替代指标
-
索提诺比率(Sortino Ratio):
- 只考虑下行波动率
- 更符合投资者的风险偏好
-
信息比率(Information Ratio):
- 考虑超额收益相对于跟踪误差的比率
- 适用于评估主动管理能力
4.2 实践建议
- 结合多个指标综合评估
- 使用滚动窗口计算,观察指标的稳定性
- 考虑市场环境的变化对指标的影响
通过以上详细分析,我们可以看到夏普比率虽然存在一些局限性,但仍然是投资组合管理中最重要和使用最广泛的指标之一。在实际应用中,需要结合其他指标和具体市场环境,做出更全面的投资决策。
5. 回答话术
夏普比率是衡量投资组合风险调整后收益的重要指标,计算公式为超额收益(投资组合收益率减去无风险利率)除以标准差。它在投资组合管理中主要用于比较不同投资组合表现、优化资产配置和评估投资经理业绩。
但夏普比率也存在局限性:假设收益率服从正态分布、对正负波动处理对称、对时间周期敏感、依赖样本期间选择等。为此,实践中建议结合索提诺比率(关注下行风险)、信息比率等多个指标,并使用滚动窗口计算,综合评估投资组合的风险收益特征。
相关文章:
的计算方法及其在投资组合管理中的应用,并说明其局限性)
100.1 AI量化面试题:解释夏普比率(Sharpe Ratio)的计算方法及其在投资组合管理中的应用,并说明其局限性
目录 0. 承前1. 夏普比率的基本概念1.1 定义与计算方法1.2 实际计算示例 2. 在投资组合管理中的应用2.1 投资组合选择2.2 投资组合优化 3. 夏普比率的局限性3.1 统计假设的限制3.2 实践中的问题 4. 改进方案4.1 替代指标4.2 实践建议 5. 回答话术 0. 承前 如果想更加全面清晰地…...

LLMs之OpenAI o系列:OpenAI o3-mini的简介、安装和使用方法、案例应用之详细攻略
LLMs之OpenAI o系列:OpenAI o3-mini的简介、安装和使用方法、案例应用之详细攻略 目录 相关文章 LLMs之o3:《Deliberative Alignment: Reasoning Enables Safer Language Models》翻译与解读 LLMs之OpenAI o系列:OpenAI o3-mini的简介、安…...

深度解析:网站快速收录与网站安全性的关系
本文转自:百万收录网 原文链接:https://www.baiwanshoulu.com/58.html 网站快速收录与网站安全性之间存在着密切的关系。以下是对这一关系的深度解析: 一、网站安全性对收录的影响 搜索引擎惩罚: 如果一个网站存在安全隐患&am…...

【Rust自学】16.2. 使用消息传递来跨线程传递数据
喜欢的话别忘了点赞、收藏加关注哦,对接下来的教程有兴趣的可以关注专栏。谢谢喵!(・ω・) 16.2.1. 消息传递 有一种很流行而且能保证安全并发的技术(或者叫机制)叫做消息传递。在这种机制里,线…...

如何实现滑动网格的功能
文章目录 1 概念介绍2 使用方法3 示例代码 我们在上一章回中介绍了SliverList组件相关的内容,本章回中将介绍SliverGrid组件.闲话休提,让我们一起Talk Flutter吧。 1 概念介绍 我们在本章回中介绍的SliverGrid组件是一种网格类组件,主要用来…...

使用C# 如何获取本机连接的WIFI名称[C# ---1]
前言 楼主最近在写一个WLAN上位机,遇到了使用C#查询SSID 的问题。CSDN上很多文章都比较老了,而且代码过于复杂。楼主自己想了一个使用CMD来获得SSID的方法 C#本身是没有获得WINDOWS网路信息的能力,必须要用系统API,WMI什么的&…...

【Docker】快速部署 Nacos 注册中心
【Docker】快速部署 Nacos 注册中心 引言 Nacos 注册中心是一个用于服务发现和配置管理的开源项目。提供了动态服务发现、服务健康检查、动态配置管理和服务管理等功能,帮助开发者更轻松地构建微服务架构。 仓库地址 https://github.com/alibaba/nacos 步骤 拉取…...

OpenCV:闭运算
目录 1. 简述 2. 用膨胀和腐蚀实现闭运算 2.1 代码示例 2.2 运行结果 3. 闭运算接口 3.1 参数详解 3.2 代码示例 3.3 运行结果 4. 闭运算的应用场景 5. 注意事项 相关阅读 OpenCV:图像的腐蚀与膨胀-CSDN博客 OpenCV:开运算-CSDN博客 1. 简述…...

Python | Pytorch | Tensor知识点总结
如是我闻: Tensor 是我们接触Pytorch了解到的第一个概念,这里是一个关于 PyTorch Tensor 主题的知识点总结,涵盖了 Tensor 的基本概念、创建方式、运算操作、梯度计算和 GPU 加速等内容。 1. Tensor 基本概念 Tensor 是 PyTorch 的核心数据结…...

aws(学习笔记第二十六课) 使用AWS Elastic Beanstalk
aws(学习笔记第二十六课) 使用aws Elastic Beanstalk 学习内容: AWS Elastic Beanstalk整体架构AWS Elastic Beanstalk的hands onAWS Elastic Beanstalk部署node.js程序包练习使用AWS Elastic Beanstalk的ebcli 1. AWS Elastic Beanstalk整体架构 官方的guide AWS…...

《OpenCV》——图像透视转换
图像透视转换简介 在 OpenCV 里,图像透视转换属于重要的几何变换,也被叫做投影变换。下面从原理、实现步骤、相关函数和应用场景几个方面为你详细介绍。 原理 实现步骤 选取对应点:要在源图像和目标图像上分别找出至少四个对应的点。这些对…...
)
9 点结构模块(point.rs)
一、point.rs源码 use super::UnknownUnit; use crate::approxeq::ApproxEq; use crate::approxord::{max, min}; use crate::length::Length; use crate::num::*; use crate::scale::Scale; use crate::size::{Size2D, Size3D}; use crate::vector::{vec2, vec3, Vector2D, V…...
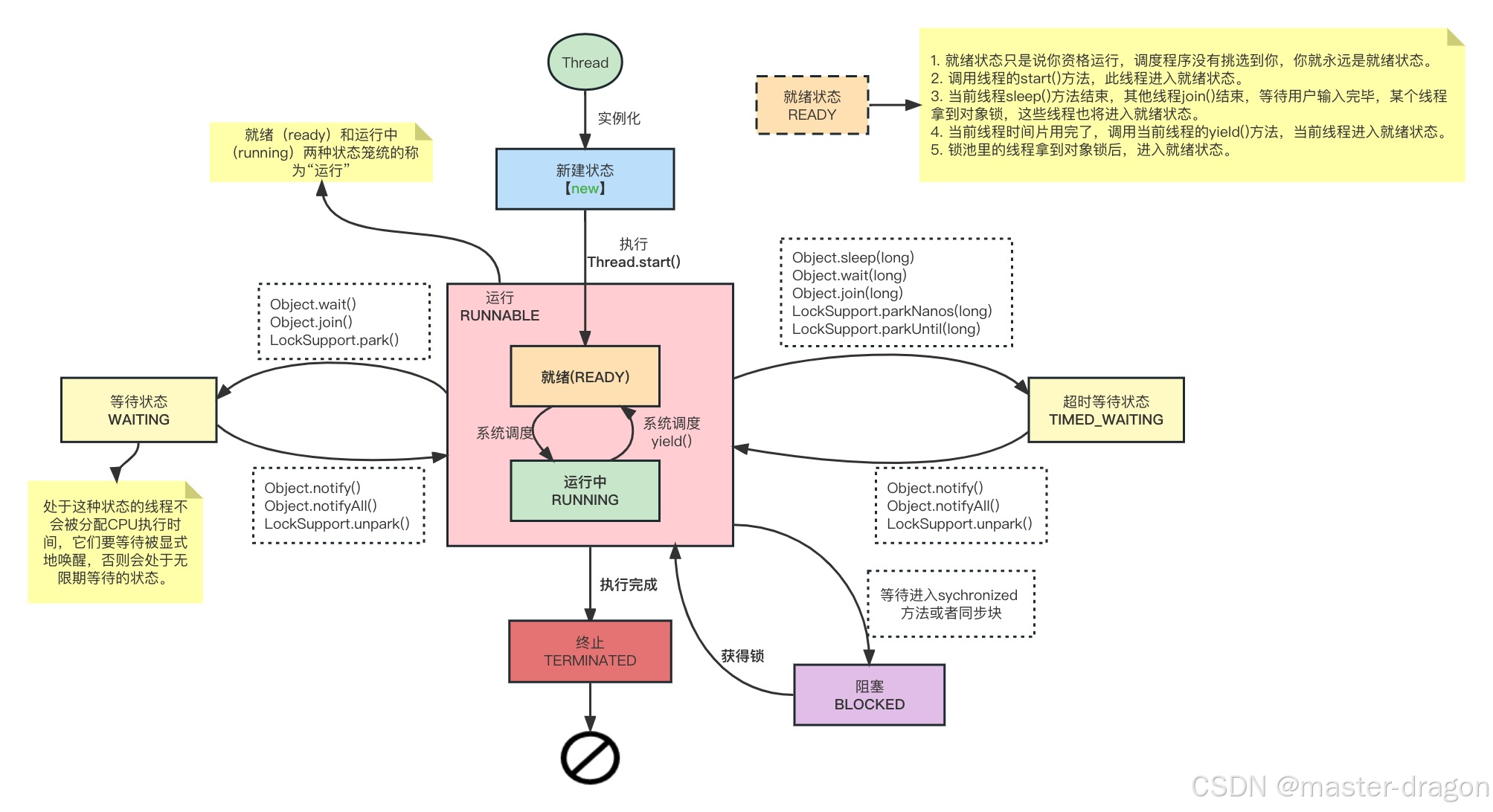
Java线程认识和Object的一些方法ObjectMonitor
专栏系列文章地址:https://blog.csdn.net/qq_26437925/article/details/145290162 本文目标: 要对Java线程有整体了解,深入认识到里面的一些方法和Object对象方法的区别。认识到Java对象的ObjectMonitor,这有助于后面的Synchron…...

【高等数学】贝塞尔函数
贝塞尔函数(Bessel functions)是数学中一类重要的特殊函数,通常用于解决涉及圆对称或球对称的微分方程。它们在物理学、工程学、天文学等多个领域都有广泛的应用,例如在波动方程、热传导方程、电磁波传播等问题中。 贝塞尔函数的…...

99.20 金融难点通俗解释:中药配方比喻马科维茨资产组合模型(MPT)
目录 0. 承前1. 核心知识点拆解2. 中药搭配比喻方案分析2.1 比喻的合理性 3. 通俗易懂的解释3.1 以中药房为例3.2 配方原理 4. 实际应用举例4.1 基础配方示例4.2 效果说明 5. 注意事项5.1 个性化配置5.2 定期调整 6. 总结7. 代码实现 0. 承前 本文主旨: 本文通过中…...

实现使用K210单片机进行猫脸检测,并在检测到猫脸覆盖屏幕50%以上时执行特定操作
要实现使用K210单片机进行猫脸检测,并在检测到猫脸覆盖屏幕50%以上时执行特定操作,以及通过WiFi上传图片到微信小程序,并在微信小程序中上传图片到开发板进行训练,可以按照以下步骤进行: 1. 硬件连接 确保K210开发板…...

小程序设计和开发:如何研究同类型小程序的优点和不足。
一、确定研究目标和范围 明确研究目的 在开始研究同类型小程序之前,首先需要明确研究的目的。是为了改进自己的小程序设计和开发,还是为了了解市场趋势和用户需求?不同的研究目的会影响研究的方法和重点。例如,如果研究目的是为了…...

tiktok 国际版抖抖♬♬ X-Bogus参数算法逆向分析
加密请求参数得到乱码,最终得到X-Bogus...

Redis 基础命令
1. redis 命令官网 https://redis.io/docs/latest/commands/ 2. 在 redis-cli 中使用 help 命令 # 查看 help string 基础命令 keys * # * 代表通配符set key value # 设置键值对del key # 删除键expire key 时间 # 给键设置时间 # -2 代表时间到期了, -1 代表…...

深入解析Python机器学习库Scikit-Learn的应用实例
深入解析Python机器学习库Scikit-Learn的应用实例 随着人工智能和数据科学领域的迅速发展,机器学习成为了当下最炙手可热的技术之一。而在机器学习领域,Python作为一种功能强大且易于上手的编程语言,拥有庞大的生态系统和丰富的机器学习库。其…...

7.4.分块查找
一.分块查找的算法思想: 1.实例: 以上述图片的顺序表为例, 该顺序表的数据元素从整体来看是乱序的,但如果把这些数据元素分成一块一块的小区间, 第一个区间[0,1]索引上的数据元素都是小于等于10的, 第二…...

Flask RESTful 示例
目录 1. 环境准备2. 安装依赖3. 修改main.py4. 运行应用5. API使用示例获取所有任务获取单个任务创建新任务更新任务删除任务 中文乱码问题: 下面创建一个简单的Flask RESTful API示例。首先,我们需要创建环境,安装必要的依赖,然后…...

【kafka】Golang实现分布式Masscan任务调度系统
要求: 输出两个程序,一个命令行程序(命令行参数用flag)和一个服务端程序。 命令行程序支持通过命令行参数配置下发IP或IP段、端口、扫描带宽,然后将消息推送到kafka里面。 服务端程序: 从kafka消费者接收…...

利用ngx_stream_return_module构建简易 TCP/UDP 响应网关
一、模块概述 ngx_stream_return_module 提供了一个极简的指令: return <value>;在收到客户端连接后,立即将 <value> 写回并关闭连接。<value> 支持内嵌文本和内置变量(如 $time_iso8601、$remote_addr 等)&a…...
)
Spring Boot 实现流式响应(兼容 2.7.x)
在实际开发中,我们可能会遇到一些流式数据处理的场景,比如接收来自上游接口的 Server-Sent Events(SSE) 或 流式 JSON 内容,并将其原样中转给前端页面或客户端。这种情况下,传统的 RestTemplate 缓存机制会…...

【入坑系列】TiDB 强制索引在不同库下不生效问题
文章目录 背景SQL 优化情况线上SQL运行情况分析怀疑1:执行计划绑定问题?尝试:SHOW WARNINGS 查看警告探索 TiDB 的 USE_INDEX 写法Hint 不生效问题排查解决参考背景 项目中使用 TiDB 数据库,并对 SQL 进行优化了,添加了强制索引。 UAT 环境已经生效,但 PROD 环境强制索…...

为什么需要建设工程项目管理?工程项目管理有哪些亮点功能?
在建筑行业,项目管理的重要性不言而喻。随着工程规模的扩大、技术复杂度的提升,传统的管理模式已经难以满足现代工程的需求。过去,许多企业依赖手工记录、口头沟通和分散的信息管理,导致效率低下、成本失控、风险频发。例如&#…...

连锁超市冷库节能解决方案:如何实现超市降本增效
在连锁超市冷库运营中,高能耗、设备损耗快、人工管理低效等问题长期困扰企业。御控冷库节能解决方案通过智能控制化霜、按需化霜、实时监控、故障诊断、自动预警、远程控制开关六大核心技术,实现年省电费15%-60%,且不改动原有装备、安装快捷、…...

跨链模式:多链互操作架构与性能扩展方案
跨链模式:多链互操作架构与性能扩展方案 ——构建下一代区块链互联网的技术基石 一、跨链架构的核心范式演进 1. 分层协议栈:模块化解耦设计 现代跨链系统采用分层协议栈实现灵活扩展(H2Cross架构): 适配层…...
可以参考以下方法:)
根据万维钢·精英日课6的内容,使用AI(2025)可以参考以下方法:
根据万维钢精英日课6的内容,使用AI(2025)可以参考以下方法: 四个洞见 模型已经比人聪明:以ChatGPT o3为代表的AI非常强大,能运用高级理论解释道理、引用最新学术论文,生成对顶尖科学家都有用的…...
