模型解释性:SHAP包的使用
本篇博客介绍另一种事后可解释性方法:SHAP(SHapley Additive exPlanation)方法。
1. Shapley值理论
Shapley值是博弈论中的一个概念,通过衡量联盟中各成员对联盟总目标的贡献程度,从而根据贡献程度来进行联盟成员的利益分配,避免了分配的平均主义。
当Shapley理论用于解释机器学习模型的时候,将输入特征xxx视为参与成员,模型输出的概率分布f(x)f(x)f(x)视为联盟总目标,通过衡量各特征的贡献度来挖掘重要特征,从而提供可解释性判断依据。其数学模型如下:g(Z′)=φ0+∑j=1MφjZj′≈f(x)(1)g(Z^{'})=\varphi_{0}+\sum_{j=1}^{M}\varphi_{j}Z^{'}_{j}\approx f(x) \tag{1}g(Z′)=φ0+j=1∑MφjZj′≈f(x)(1)其中,ggg是解释模型,f(x)f(x)f(x)是原机器学习模型,Zj′={0,1}MZ^{'}_{j}=\{0,1\}^{M}Zj′={0,1}M表示相应特征是否被观察到,MMM是输入特征的数目,φi\varphi_{i}φi是每个特征的归因值,φ0\varphi_{0}φ0是解释模型的常数。
对于一个特定的输入数据x0x_{0}x0,其Shapley值的计算公式如下:φi(f,x0)=∑S⊆NS/{i}∣S∣!(M−∣S∣−1)!∣NS∣\varphi_{i}(f,x_{0})=\sum_{S\subseteq N_{S}/ \{i\}}\frac{|S|!(M-|S|-1)!}{|N_{S}|!}[f(S\cup\{i\})-f(S)]\tag{2}φi(f,x0)=S⊆NS/{i}∑∣NS∣!∣S∣!(M−∣S∣−1)其中,φi(f)\varphi_{i}(f)φi(f)代表函数fff中特征iii的贡献度,NSN_{S}NS是所有特征组成的集合,SSS代表特征子集,NS/{i}N_{S}/\{i\}NS/{i}代表在集合NSN_{S}NS中去除特征iii,S∪{i}S\cup \{i\}S∪{i}表示子集SSS中增加特征iii,∣S∣|S|∣S∣表示集合SSS中元素的个数。
为了方面公式(2)的计算,通常将公式(2)转化为如下公式计算:φi(f,x0)=∑z′∈{0,1}M∣z′∣!(M−∣z′∣−1)!M\varphi_{i}(f,x_{0})=\sum_{z^{'}\in\{0,1\}^{M}}\frac{|z^{'}|!(M-|z^{'}|-1)!}{M!}[f_{S}(z^{'})-f_{S}(z^{'}|i)]\tag{3}φi(f,x0)=z′∈{0,1}M∑M!∣z′∣!(M−∣z′∣−1)其中,fS=E[f(x)∣zS′]=1N∑j=1Nf(xj′)f_{S}=E[f(x)|z_{S}^{'}]=\frac{1}{N}\sum_{j=1}^{N}f(x_{j}^{'})fS=E[f(x)∣zS′]=N1j=1∑Nf(xj′)其中,zS′z_{S}^{'}zS′为集合SSS中特征的取值所组成的集合,NNN为原函数fff训练数据的个数,xj′x_{j}^{'}xj′的取值如下:xj′={x0i,Fi∈zS′xji,Fi∉zS′x_{j}^{'}=\left\{\begin{aligned} x_{0i},& F_{i}\in z_{S}^{'} \\ x_{ji},&F_{i}\notin z_{S}^{'} \end{aligned}\right. xj′={x0i,xji,Fi∈zS′Fi∈/zS′其中,x0ix_{0i}x0i为待解释数据x0x_{0}x0的第iii个特征值,xjix_{ji}xji表示第jjj个训练数据中第iii个特征的取值,FiF_{i}Fi表示第iii个特征值。
SHAP值具备扎实的理论基础,但φi\varphi_{i}φi的计算复杂度和E[f(x)∣zS′]E[f(x)|z_{S}^{'}]E[f(x)∣zS′]的有效估计是其在实际应用中的最大阻碍,为了解决这个问题,Lundberg等人提出了Tree SHAP方法。
Tree SHAP是用于树模型的快速SHAP值估计方法,大大增加了SHAP值的实际应用能力。
2 SHAP包用法
这里仍然以Boston房价为例,使用XGBoost方法训练模型。其用法举例如下:
模型训练
import pandas as pd
import numpy as np
from sklearn.datasets import load_boston
from xgboost import XGBRegressor
from sklearn.model_selection import train_test_split
import shap
shap.initjs()
#分类
boston=load_boston()
X=boston.data
y=boston.target
features=boston.feature_names
X_train,X_test,y_train,y_test=train_test_split(X,y,test_size=0.2,random_state=0)xgbr=XGBRegressor(n_estimators=200,max_depth=4)
xgbr.fit(X_train,y_train)
对单个样本进行解释
explainer=shap.TreeExplainer(xgbr)
shap_values=explainer.shap_values(X_test[1].reshape(1,-1))
shap.force_plot(explainer.expected_value,shap_values,X_test[1].reshape(1,-1),feature_names=features)
其结果如下:

关于上图,有以下几个方面需要说明:
- base_value:全体样本Shape平均值,这里的全体样本指的是模型的训练样本;
- output_value: 当前样本的Shap输出值,即为模型的预测值;
- 正向作用特征:红色特征即为正向作用的特征;
- 反向作用特征:蓝色特征即为反向作用的特征;
整个测试集的Shap分布
explainer=shap.TreeExplainer(xgbr)
shap_values=explainer.shap_values(X_test)
shap.force_plot(explainer.expected_value,shap_values,X_test,feature_names=features)
其结果如下(可以通过调节横纵坐标观察当个特征的效果):

从特征角度观察样本Shap值
shap.summary_plot(shap_values,X_test,feature_names=features)
其结果如下:

参考文献
- 《基于图模型机器学习算法的可解释性技术研究与实现》
- 《稳定评估机器学习模型可解释性研究》
- https://blog.csdn.net/tMb8Z9Vdm66wH68VX1/article/details/106131890
相关文章:

模型解释性:SHAP包的使用
本篇博客介绍另一种事后可解释性方法:SHAP(SHapley Additive exPlanation)方法。 1. Shapley值理论 Shapley值是博弈论中的一个概念,通过衡量联盟中各成员对联盟总目标的贡献程度,从而根据贡献程度来进行联盟成员的利益分配,避免…...

算法训练营 day45 动态规划 0-1背包理论 分割等和子集
算法训练营 day45 动态规划 0-1背包理论 分割等和子集 0-1背包理论 有n件物品和一个最多能背重量为w 的背包。第i件物品的重量是weight[i],得到的价值是value[i] 。每件物品只能用一次,求解将哪些物品装入背包里物品价值总和最大。 在下面的讲解中&…...

SSM框架
1.mybatis的底层原理 本质上就是使用反射和动态代理来实现对应的映射关系 2.日志级别 3.传递参数 单个参数的传递和多个参数的传递 Emp selectOne(Param(“xingming”) String name); List selectByCondition(Param(“name”) String name,Param(“sal”) double sal); 4.#和…...

教育行业需要什么样的客服系统?
某教育公司拥有素质教育、成人教育、智慧教育等多个业务板块,日常通过电商、线上媒体、线上线下授课等方式进行业务开展和品牌宣传,取得了非常不错的成绩,受到了很多人的好评反馈。 对于这样一个教育公司,客户来源广泛࿰…...

花房集团任命新首席财务官:已跌破IPO发行价,活跃用户下滑
上市刚满2个月,花椒母公司花房集团(HK:03611)的高管就发生了变更。2023年2月12日,花房集团披露的公告显示,董事会宣布赵磊为该公司首席财务官(CFO),自2023年2月10日起生效。 据贝多…...

儿童绘本馆图书借阅租赁知识付费小程序源码交流
1.分类图书 2.书单推荐 4.会员卡次、期限购买 5.借阅时间选择 6.积分签到 7.优惠Q领取 前端uniapp开发 后端thinkphp开发 完全开源 <template> <view class"sp-section sp-index"> <!-- search --> <view class&qu…...

Vue3 中 axios 的安装及使用
目录前言:一、什么是 axios ?二、Axios 的配置项三、Axios 的请求方式四、自定义创建实例五、Axios 请求错误处理六、Axios 解决跨域问题七、Axios 请求案例随机笑话大全总结:前言: 在编写vue里的项目时,必须要用和后台…...

Django设计模式以及模板层介绍
MVC和MTV 传统的MVC作用:降低模块间的耦合度(解耦)Django的MTV模式 作用:降低模块间的耦合度(解耦)什么是模板 1、模板是可以根据字典数据动态变化的html网页2、模板可以根据视图中传递的字典数据动态生成相…...

Linux信号一门搞定
1.信号是什么? 信号其实就是一个软件中断。 例: 输入命令,在Shell下启动一个前台进程。用户按下Ctrl-C,键盘输入产生一个硬件中断。如果CPU当前正在执行这个进程的代码,则该进程的用户空间代码暂停执行,…...

手撸一个动态Feign,实现一个“万能”接口调用
Feign,在微服务框架中,是的服务直接的调用变得很简洁、简单,而不需要再编写Java Http调用其他微服务的接口。 动态feign 对于fegin调用,我们一般的用法:为每个微服务都创建对应的feignclient接口,然后为每…...
Linux Capabilities 入门
目录 Linux capabilities 是什么? capabilities 的赋予和继承 线程的 capabilities Permitted Effective Inheritable Bounding Ambient 文件的 capabilities Permitted Inheritable Effective 运行 execve() 后 capabilities 的变化 案例 Linux capab…...

驱动 day6
关于设备树的理解: 设备树(Device Tree)是一种用于特定硬件设备的解释语法树。它用来表示存储有关主板硬件和CPU架构信息的数据在内核中的传递格式,使内核可以更好地了解硬件并支持它们,而不必编写固定的代码。设备节点…...
附录2-tensorflow目标检测
源码来自作者Bubbliiiing,我对参考链接的代码略有修改,网盘地址 链接:百度网盘 请输入提取码 提取码:dvb1 目录 1 参考链接 2 环境 3 数据集准备 3.1 VOCdevkit/VOC2007 3.2 model_data/voc_classes.txt 3.3 voc_an…...

常见的EMC问题
电磁兼容设计的目的就在于满足产品功能要求、减少调试时间,使产品满足电磁兼容标准的要求,并且使产品不会对系统中的其它设备产生电磁干扰。 电磁兼容设计中常见的问题有哪些? 1、电磁兼容设计可以从电路设计(包括器件选择&…...

Redis内存存储效率问题
目录 内存碎片是如何形成的? 如何判断是否有内存碎片? 如何清理内存碎片? INFO命令 面向 Prometheus 的 Redis-exporter 监控 实习期间,了解到,企业级开发中多个项目使用Redis,运行Redis实例的有可能是…...
3.28 haas506 2.0开发教程-example-蓝牙多设备扫描(仅支持M320,HD1)
haas506 2.0开发教程-example-蓝牙多设备扫描案例说明蓝牙信息克隆1.手机蓝牙改名信息克隆代码测试案例说明 开发板扫描蓝牙设备,获取并打印蓝牙设备mac地址。mac地址每个设备不同,且不能更改。本案例仅适用于M320开发板和HD1-RTU。案例使用手机与iBeac…...
C语言经典编程题100例(41~60)
目录41、习题4-4 特殊a串数列求和42、习题4-6 水仙花数43、习题4-7 最大公约数和最小公倍数44、习题7-5 找鞍点45、练习5-1 求m到n之和46、练习5-2 找两个数中最大者47、练习5-3 数字金字塔48、习题5-1 符号函数49、习题5-2 使用函数求奇数和50、习题5-3 使用函数计算两点间的距…...
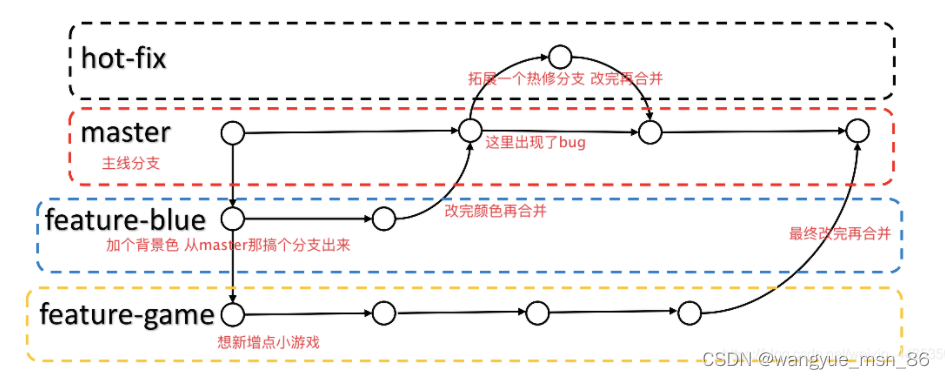
git日常使用命令
实习这段时间使用了很多git指令来提交代码,简单记录一下日常使用的指令: 提交代码通常顺序: 1.git status 查看本地修改项 2.git add . 提交全部文件 (这个 .是全部文件)到暂存区 3.git commit -m ‘本次提交的说明’…...

ES6对象展开运算符浅拷贝or深拷贝
ES6中提出的对象展开运算符“…”就是用来展开元素的。有了它就不用代码循环遍历了,偷懒专用。 1. 合并数组 展开原有数组中的所有元素,可以合并成一个新的数组。 var a[1,2,3]; var b[4,5,6]; var c[...a,...b]; console.log(c) // 输出:…...

leaflet 上传包含shp的zip文件,在map上解析显示图形(059)
第059个 点击查看专栏目录 本示例的目的是介绍演示如何在vue+leaflet中本地上传包含shp的zip文件,利用shapefile读取shp数据,并在地图上显示图形。 直接复制下面的 vue+openlayers源代码,操作2分钟即可运行实现效果 文章目录 示例效果加载shapefile.js方式安装引用jszip(…...

铭豹扩展坞 USB转网口 突然无法识别解决方法
当 USB 转网口扩展坞在一台笔记本上无法识别,但在其他电脑上正常工作时,问题通常出在笔记本自身或其与扩展坞的兼容性上。以下是系统化的定位思路和排查步骤,帮助你快速找到故障原因: 背景: 一个M-pard(铭豹)扩展坞的网卡突然无法识别了,扩展出来的三个USB接口正常。…...

地震勘探——干扰波识别、井中地震时距曲线特点
目录 干扰波识别反射波地震勘探的干扰波 井中地震时距曲线特点 干扰波识别 有效波:可以用来解决所提出的地质任务的波;干扰波:所有妨碍辨认、追踪有效波的其他波。 地震勘探中,有效波和干扰波是相对的。例如,在反射波…...

Appium+python自动化(十六)- ADB命令
简介 Android 调试桥(adb)是多种用途的工具,该工具可以帮助你你管理设备或模拟器 的状态。 adb ( Android Debug Bridge)是一个通用命令行工具,其允许您与模拟器实例或连接的 Android 设备进行通信。它可为各种设备操作提供便利,如安装和调试…...

通过Wrangler CLI在worker中创建数据库和表
官方使用文档:Getting started Cloudflare D1 docs 创建数据库 在命令行中执行完成之后,会在本地和远程创建数据库: npx wranglerlatest d1 create prod-d1-tutorial 在cf中就可以看到数据库: 现在,您的Cloudfla…...

基于uniapp+WebSocket实现聊天对话、消息监听、消息推送、聊天室等功能,多端兼容
基于 UniApp + WebSocket实现多端兼容的实时通讯系统,涵盖WebSocket连接建立、消息收发机制、多端兼容性配置、消息实时监听等功能,适配微信小程序、H5、Android、iOS等终端 目录 技术选型分析WebSocket协议优势UniApp跨平台特性WebSocket 基础实现连接管理消息收发连接…...

跨链模式:多链互操作架构与性能扩展方案
跨链模式:多链互操作架构与性能扩展方案 ——构建下一代区块链互联网的技术基石 一、跨链架构的核心范式演进 1. 分层协议栈:模块化解耦设计 现代跨链系统采用分层协议栈实现灵活扩展(H2Cross架构): 适配层…...

从零实现STL哈希容器:unordered_map/unordered_set封装详解
本篇文章是对C学习的STL哈希容器自主实现部分的学习分享 希望也能为你带来些帮助~ 那咱们废话不多说,直接开始吧! 一、源码结构分析 1. SGISTL30实现剖析 // hash_set核心结构 template <class Value, class HashFcn, ...> class hash_set {ty…...

sipsak:SIP瑞士军刀!全参数详细教程!Kali Linux教程!
简介 sipsak 是一个面向会话初始协议 (SIP) 应用程序开发人员和管理员的小型命令行工具。它可以用于对 SIP 应用程序和设备进行一些简单的测试。 sipsak 是一款 SIP 压力和诊断实用程序。它通过 sip-uri 向服务器发送 SIP 请求,并检查收到的响应。它以以下模式之一…...

【7色560页】职场可视化逻辑图高级数据分析PPT模版
7种色调职场工作汇报PPT,橙蓝、黑红、红蓝、蓝橙灰、浅蓝、浅绿、深蓝七种色调模版 【7色560页】职场可视化逻辑图高级数据分析PPT模版:职场可视化逻辑图分析PPT模版https://pan.quark.cn/s/78aeabbd92d1...

push [特殊字符] present
push 🆚 present 前言present和dismiss特点代码演示 push和pop特点代码演示 前言 在 iOS 开发中,push 和 present 是两种不同的视图控制器切换方式,它们有着显著的区别。 present和dismiss 特点 在当前控制器上方新建视图层级需要手动调用…...
