链表题目总结 -- 递归
目录
- 一. 递归反转整个链表
- 1. 思路简述
- 2. 代码
- 3. 总结
- 二. 反转链表前 N 个节点
- 1. 思路简述
- 2. 代码
- 3. 总结
- 三、反转链表的一部分
- 1. 思路简述
- 2. 代码
- 3.总结
- 四、从节点M开始反转后面的链表
- 1. 思路简述
- 2. 代码
- 3.总结
一. 递归反转整个链表
- 题目链接:https://leetcode.cn/problems/reverse-linked-list/
1. 思路简述
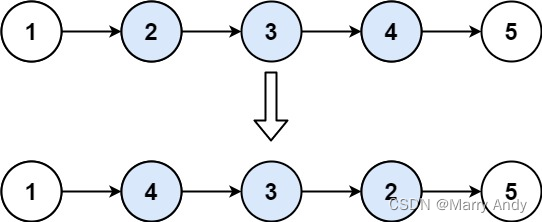
- 所谓递归,就像那句歌词一样“一层一层剥开我的心”,我们从第一个节点一直向下探索,发现节点5。现在想:如果是单个节点,那反转链表其实就相当于自身本身,也就是不用动了。这里考虑一个临界情况,如果传进的参数(head指针)是null,那也不用动了,直接返回其本身就可以。
- 来到倒数第二层,也就是节点4,现在情况变成了节点有2个的链表,现在需要反转,那么我们只需要将中间的指针做一个反转就好了,而当前传进来的指针(head),其实是节点4的head指针,那么就有head.next.next = head;,最后将节点4的后继赋值为空(head.next = null),这表示这一阶段(有2个节点的链表已经反转完成。如果链表只有两个节点,直接输出就可以。)
- 重复上面步骤,直到最后整个链表都反转了
2. 代码
/*** Definition for singly-linked list.* public class ListNode {* int val;* ListNode next;* ListNode() {}* ListNode(int val) { this.val = val; }* ListNode(int val, ListNode next) { this.val = val; this.next = next; }* }*/
class Solution { public ListNode reverseList(ListNode head) {//从后向前,一点点的进行反转//先分析特殊情况,链表有一个节点或者没有节点,直接返回头结点if(head == null || head.next == null)return head;else{//last为反转链表之后的头指针ListNode last = reverseList(head.next);head.next.next = head;head.next = null;return last;}}
}
3. 总结
- 时间复杂度:o(n)
- 空间复杂度:o(n),需要用栈
- 第一次做的时候,还以为是逆向输出,整了半天,搞错了。
- 对递归的边界条件掌握的还是不好,像head == null这一块,博主当时就没想到与head.next进行合并。
- head.next = null;一定要注意,否则,会出现成环的现象
二. 反转链表前 N 个节点
- 题目链接:没有链接,给一个函数名:public static ListNode reverseN(ListNode head,int n);,自己去练吧。
1. 思路简述
- 本质和反转链表差不多,只是在边界值的地方需要注意,
2. 代码
//存放需要逆转链表的后继第一个节点public static ListNode successor = null;public static ListNode reverseN(ListNode head,int n){//逆转前n个节点if (n == 1) {successor = head.next;return head;}//递归,将下一个节点放进去ListNode last = reverseN(head.next, n - 1);head.next.next = head;head.next = successor;return last;}
3. 总结
- 也就是反转链表,只是每次反转完,head后面要接后继节点(后面的一段不需要反转的链表),就变了这一点。
- 时间复杂度:o(n)
- 空间复杂度:o(n),需要用栈
三、反转链表的一部分
- 题目链接:https://leetcode.cn/problems/reverse-linked-list-ii/
1. 思路简述
- 将问题转换成反转前n个节点的问题。
2. 代码
//存放需要逆转链表的后继第一个节点public static ListNode successor = null;public static ListNode reverseN(ListNode head,int n){//逆转前n个节点if (n == 1) {successor = head.next;return head;}//递归,将下一个节点放进去ListNode last = reverseN(head.next, n - 1);head.next.next = head;head.next = successor;return last;}ListNode reverseBetween(ListNode head, int m, int n) {// 当m为1的时候,装换成了反转前面几个节点的链表的问题if (m == 1) {return reverseN(head, n);}// 将前面不需要反转的链表和后面反转过的链表接在一起head.next = reverseBetween(head.next, m - 1, n - 1);return head;}
3.总结
- head.next = reverseBetween(head.next, m - 1, n - 1); 为什么是head.next呢,看边界情况,m = 1时,返回的是后面已经反转过的链表,也就是说前面的链表压根不需要反转,只要把它们拼接在一起就行了。
- 再说为什么是m - 1的问题,每递归一次,新链表就会从前面缩短一节,那么对于新链表来说,就是从第m-1个节点开始反转,到第n - 1个节点结束反转。这里的关键是链表从头开始缩短了,所以,m - 1 和 n - 1都要存在。
四、从节点M开始反转后面的链表
- 题目链接:没有链接,给一个函数名:public static ListNode reverseP(ListNode head,int m);,自己去练吧。
1. 思路简述
- 转换成反转单链表的问题
2. 代码
public ListNode reverseList(ListNode head) {//从后向前,一点点的进行反转//先分析特殊情况,链表有一个节点或者没有节点,直接返回头结点if(head == null || head.next == null)return head;else{//last为反转链表之后的头指针ListNode last = reverseList(head.next);head.next.next = head;head.next = null;return last;}}public static ListNode reverseP(ListNode head, int m){//转换成反转链表的问题if(m == 1){return reverseList(head);}head.next = reverseP(head.next, m - 1);return head;}
3.总结
- 和上一题差不多,一直递归,到链表需要反转的地方(m == 1),开始反转整个单链表。
参考:https://labuladong.github.io/algo/di-yi-zhan-da78c/shou-ba-sh-8f30d/di-gui-mo–10b77/
相关文章:

链表题目总结 -- 递归
目录一. 递归反转整个链表1. 思路简述2. 代码3. 总结二. 反转链表前 N 个节点1. 思路简述2. 代码3. 总结三、反转链表的一部分1. 思路简述2. 代码3.总结四、从节点M开始反转后面的链表1. 思路简述2. 代码3.总结一. 递归反转整个链表 题目链接:https://leetcode.cn/…...
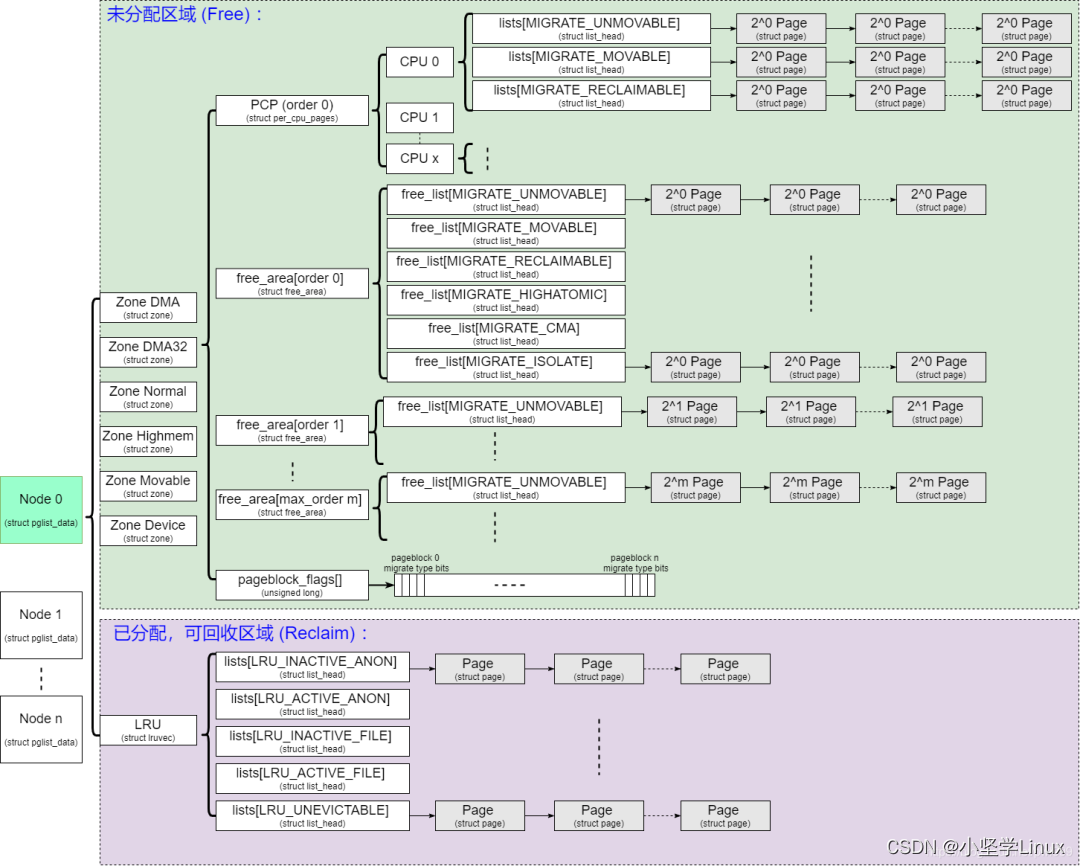
重写-linux内存管理-伙伴分配器(一)
文章目录一、伙伴系统的结构二、初始化三、分配内存3.1 prepare_alloc_pages3.2 get_page_from_freelist3.2.1 zone_watermark_fast3.2.2 zone_watermark_ok3.2.3 rmqueue3.2.3.1 rmqueue_pcplist3.2.3.2 __rmqueue3.2.3.2.1 __rmqueue_smallest3.2.3.2.2 __rmqueue_fallback3.…...
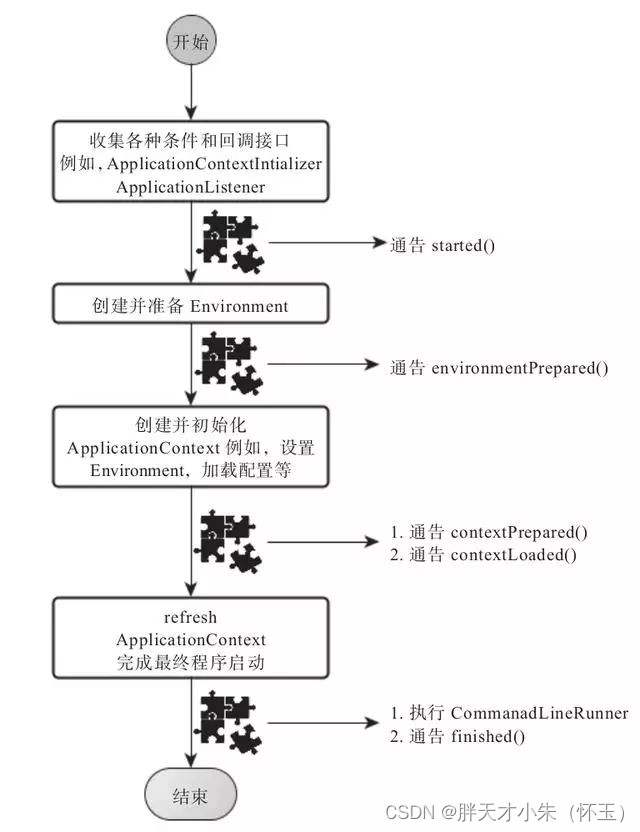
为什么要用springboot进行开发呢?
文章目录前言1、那么Springboot是怎么实现自动配置的1.1 启动类1.2 SpringBootApplication1.3 Configuration1.4 ComponentScan1.5 EnableAutoConfiguration1.6 两个重要注解1.7 AutoConfigurationPackage注解1.8 Import(AutoConfigurationImportSelector.class)注解1.9自动配置…...

设备树信息解析相关函数
一。可以通过三种不同的方式解析设备树节点: 1.根据设备树节点的名字解析设备树节点 struct device_node *of_find_node_by_name(struct device_node *from, const char *name); 参数: from:当前节点父节点首地址 name:设备树节点名字 …...

LeetCode-1124. 表现良好的最长时间段【哈希表,前缀和,单调栈】
LeetCode-1124. 表现良好的最长时间段【哈希表,前缀和,单调栈】题目描述:解题思路一:查字典。cur是当前的前缀和(劳累与不劳累天数之差),向前遍历。有两种情况。情况一,若cur大于0则是[0,i]的劳累与不劳累天…...
vue-router路由配置
介绍:路由配置主要是用来确定网站访问路径对应哪个文件代码显示的,这里主要描述路由的配置、子路由、动态路由(运行中添加删除路由) 1、npm添加 npm install vue-router // 执行完后会自动在package.json中添加 "vue-router…...

中国计算机设计大赛来啦!用飞桨驱动智慧救援机器狗
中国大学生计算机设计大赛是我国高校面向本科生最早的赛事之一,自2008年开赛至今,一直由教育部高校与计算机相关教指委等或独立或联合主办。大赛的目的是以赛促学、以赛促教、以赛促创,为国家培养德智体美劳全面发展的创新型、复合型、应…...

嘉定区2022年高新技术企业认定资助申报指南
各镇人民政府,街道办事处,嘉定工业区、菊园新区管委会,各相关企业: 为推进实施创新驱动发展战略,加快建设具有全球影响力的科技创新中心,根据《嘉定区关于加快本区高新技术企业发展的实施方案(…...

【C++】关键字、命名空间、输入和输出、缺省参数、函数重载
C关键字(C98)命名空间产生背景命名空间定义命名空间使用输入&输出缺省参数什么叫缺省参数缺省参数分类函数重载函数重载概念C支持函数重载的原理--名字修饰C关键字(C98) C总计63个关键字,C语言32个关键字。 下面我们先看一下C有多少关键字,不对关键…...

【一道面试题】关于HashMap的一系列问题
HashMap底层数据结构在1.7与1.8的变化 1.7是基于数组链表实现的,1.8是基于数组链表红黑树实现的,链表长度达到8时会树化 使用哈希表的好处 使用hash表是为了提升查找效率,比如我现在要在数组中查找一个A对象,在这种情况下是无法…...

论文笔记: Monocular Depth Estimation: a Review of the 2022 State of the Art
中文标题:单目深度估计:回顾2022年最先进技术 本文对比了物种最近的基于深度学习的单目深度估计方法: GPLDepth(2022)[15]: Global-Local Path Networks for Monocular Depth Estimation with Vertical CutDepthAdabins(2021)[1]: Adabins:…...
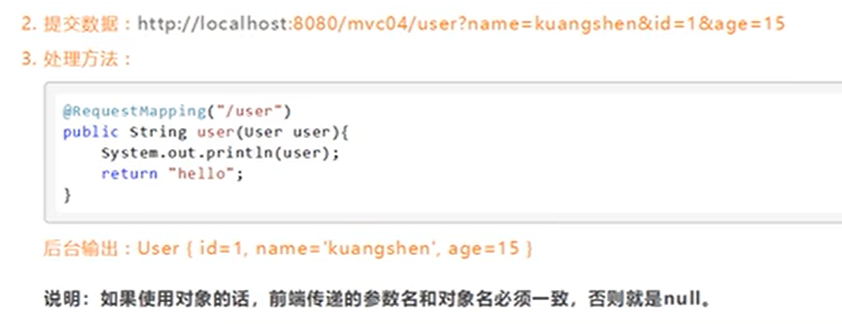
Springmvc补充配置
Controller配置总结 控制器通常通过接口定义或注解定义两种方法实现 在用接口定义写控制器时,需要去Spring配置文件中注册请求的bean;name对应请求路径,class对应处理请求的类。 <bean id"/hello" class"com.demo.Controller.HelloCo…...

MySQL 的 datetime等日期和时间处理SQL函数及格式化显示
MySQL 的 datetime等日期和时间处理SQL函数及格式化显示MySQL 时间相关的SQL函数:MySQL的SQL DATE_FORMAT函数:用于以不同的格式显示日期/时间数据。DATE_FORMAT(date, format) 根据格式串 format 格式化日期或日期和时间值 date,返回结果串。…...

基于微信云开发的防诈反诈宣传教育答题小程序
基于微信云开发的防诈反诈宣传教育答题小程序一、前言介绍作为当代大学生,诈骗事件的发生屡见不鲜,但却未能引起大家的重视。高校以线上宣传、阵地展示为主,线下学习、实地送法为辅,从而构筑立体化反诈骗防线。在线答题考试是一种…...
Map和Set
Map和set是一种专门用来进行搜索的容器或者数据结构,其搜索的效率与其具体的实例化子类有关。数据的一般查找方式有两种:直接遍历和二分查找。但这两种查找方式都有很大的局限性,也不便于对数据进行增删查改等操作。对于这一类数据的查找&…...
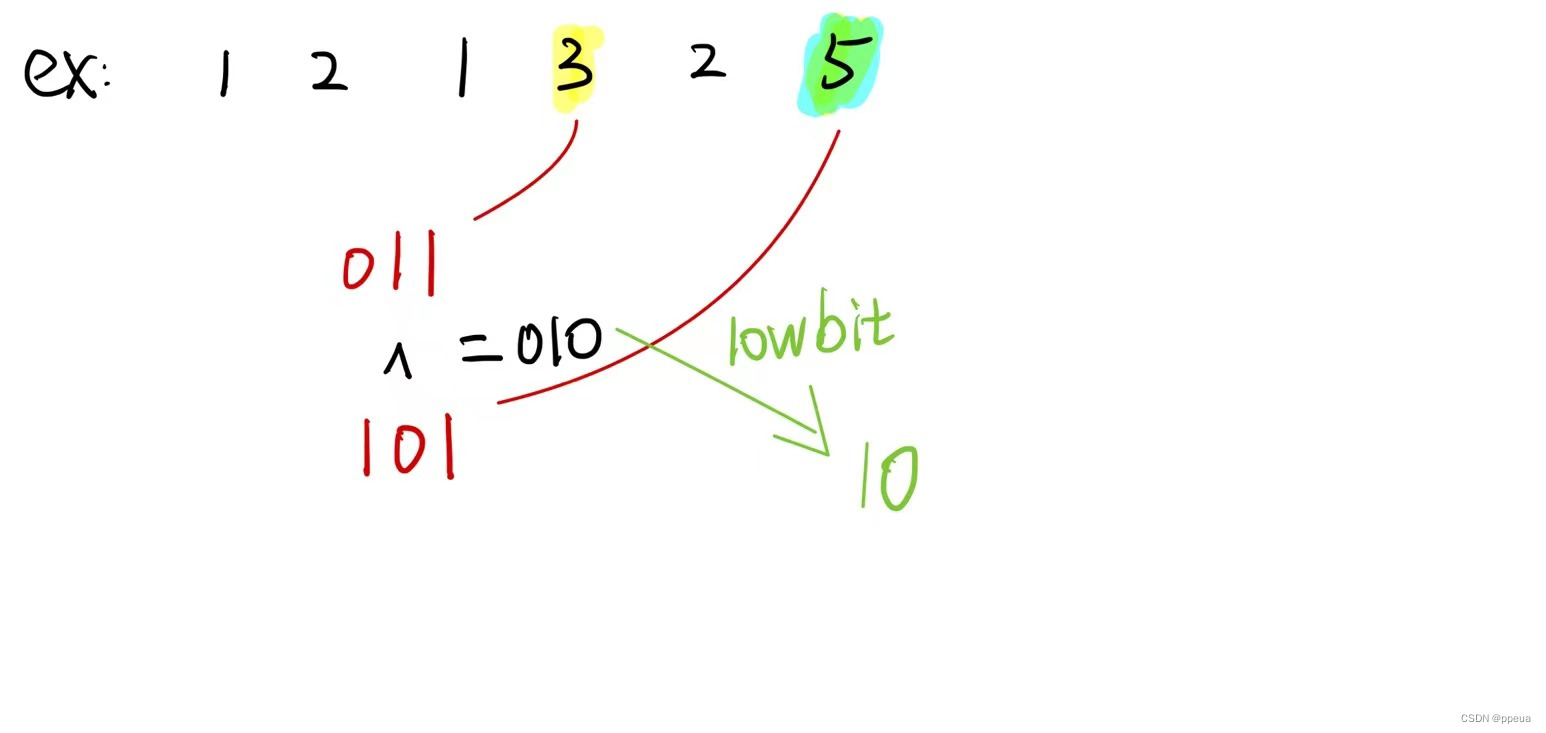
【位运算问题】Leetcode 136、137、260问题详解及代码实现
Halo,这里是Ppeua。平时主要更新C语言,C,数据结构算法......感兴趣就关注我吧!你定不会失望。 🌈个人主页:主页链接 🌈算法专栏:专栏链接 我会一直往里填充内容哒! &…...

同花顺2023届春招内推
同花顺2023届春招开始啦! 同花顺是国内首家上市的互联网金融信息服务平台,如果你对互联网金融感兴趣,如果你有志向在人工智能方向发挥所长,如果你也是一个激情澎湃的小伙伴,欢迎加入我们!岗位类别…...
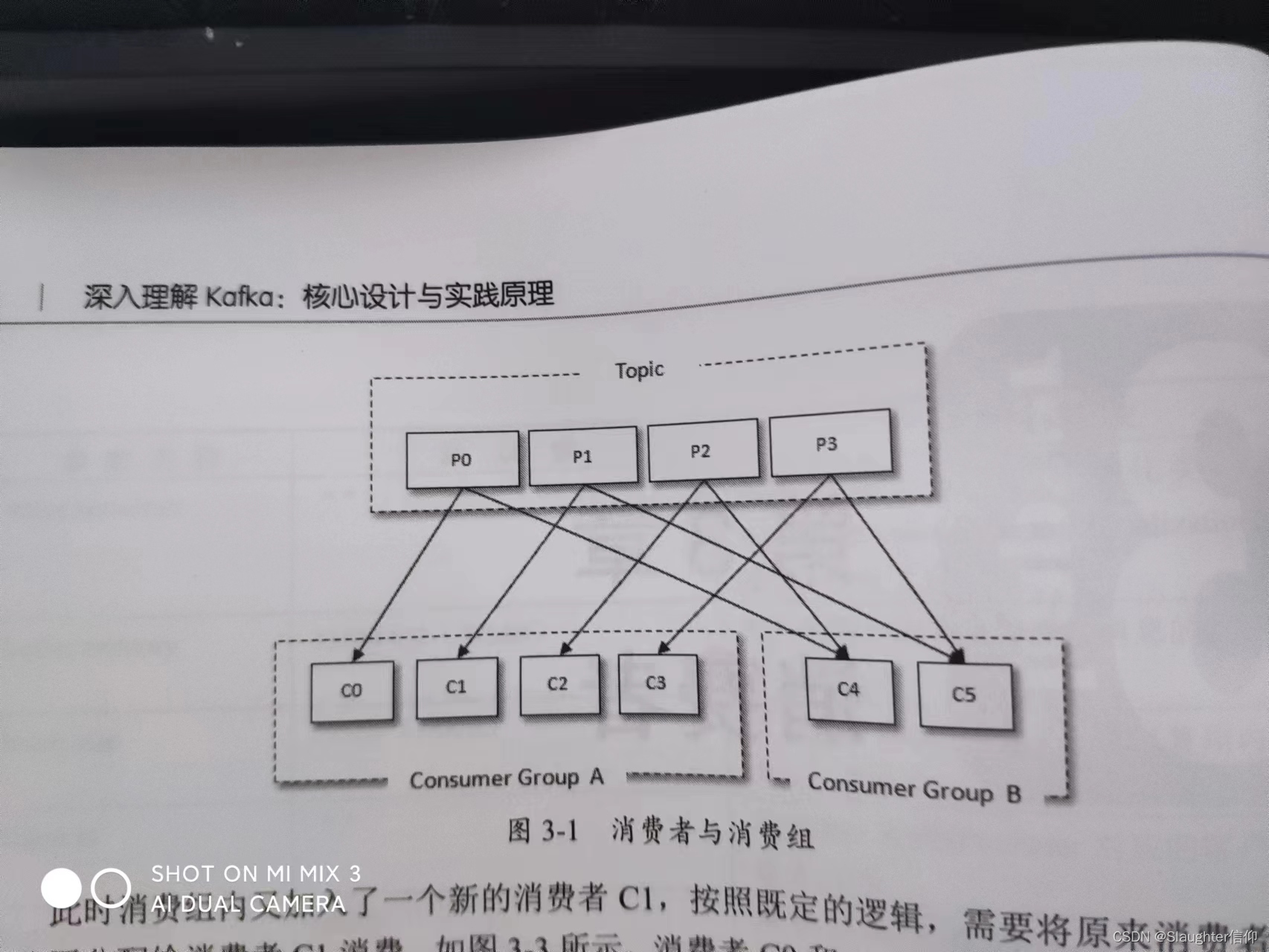
深入Kafka核心设计与实践原理读书笔记第三章消费者
消费者 消费者与消费组 消费者Consumer负责定于kafka中的主题Topic,并且从订阅的主题上拉取消息。与其他消息中间件不同的在于它有一个消费组。每个消费者对应一个消费组,当消息发布到主题后,只会被投递给订阅它的消费组的一个消费者。 如…...

IDEA 中使用 Git 图文教程详解
✅作者简介:2022年博客新星 第八。热爱国学的Java后端开发者,修心和技术同步精进。 🍎个人主页:Java Fans的博客 🍊个人信条:不迁怒,不贰过。小知识,大智慧。 💞当前专栏…...

【Linux系统】进程概念
目录 1 冯诺依曼体系结构 2 操作系统(Operator System) 概念 设计OS的目的 定位 总结 系统调用和库函数概念 3 进程 3.1 基本概念 3.2 描述进程-PCB 3.2 组织进程 3.3 查看进程 3.4 通过系统调用获取进程标示符 3.5 进程状态 在了解进程概念前我们还得了解下冯诺…...

19c补丁后oracle属主变化,导致不能识别磁盘组
补丁后服务器重启,数据库再次无法启动 ORA01017: invalid username/password; logon denied Oracle 19c 在打上 19.23 或以上补丁版本后,存在与用户组权限相关的问题。具体表现为,Oracle 实例的运行用户(oracle)和集…...

多模态2025:技术路线“神仙打架”,视频生成冲上云霄
文|魏琳华 编|王一粟 一场大会,聚集了中国多模态大模型的“半壁江山”。 智源大会2025为期两天的论坛中,汇集了学界、创业公司和大厂等三方的热门选手,关于多模态的集中讨论达到了前所未有的热度。其中,…...

深入剖析AI大模型:大模型时代的 Prompt 工程全解析
今天聊的内容,我认为是AI开发里面非常重要的内容。它在AI开发里无处不在,当你对 AI 助手说 "用李白的风格写一首关于人工智能的诗",或者让翻译模型 "将这段合同翻译成商务日语" 时,输入的这句话就是 Prompt。…...

SkyWalking 10.2.0 SWCK 配置过程
SkyWalking 10.2.0 & SWCK 配置过程 skywalking oap-server & ui 使用Docker安装在K8S集群以外,K8S集群中的微服务使用initContainer按命名空间将skywalking-java-agent注入到业务容器中。 SWCK有整套的解决方案,全安装在K8S群集中。 具体可参…...

【kafka】Golang实现分布式Masscan任务调度系统
要求: 输出两个程序,一个命令行程序(命令行参数用flag)和一个服务端程序。 命令行程序支持通过命令行参数配置下发IP或IP段、端口、扫描带宽,然后将消息推送到kafka里面。 服务端程序: 从kafka消费者接收…...

微信小程序之bind和catch
这两个呢,都是绑定事件用的,具体使用有些小区别。 官方文档: 事件冒泡处理不同 bind:绑定的事件会向上冒泡,即触发当前组件的事件后,还会继续触发父组件的相同事件。例如,有一个子视图绑定了b…...

Python:操作 Excel 折叠
💖亲爱的技术爱好者们,热烈欢迎来到 Kant2048 的博客!我是 Thomas Kant,很开心能在CSDN上与你们相遇~💖 本博客的精华专栏: 【自动化测试】 【测试经验】 【人工智能】 【Python】 Python 操作 Excel 系列 读取单元格数据按行写入设置行高和列宽自动调整行高和列宽水平…...

抖音增长新引擎:品融电商,一站式全案代运营领跑者
抖音增长新引擎:品融电商,一站式全案代运营领跑者 在抖音这个日活超7亿的流量汪洋中,品牌如何破浪前行?自建团队成本高、效果难控;碎片化运营又难成合力——这正是许多企业面临的增长困局。品融电商以「抖音全案代运营…...

el-switch文字内置
el-switch文字内置 效果 vue <div style"color:#ffffff;font-size:14px;float:left;margin-bottom:5px;margin-right:5px;">自动加载</div> <el-switch v-model"value" active-color"#3E99FB" inactive-color"#DCDFE6"…...

Vue2 第一节_Vue2上手_插值表达式{{}}_访问数据和修改数据_Vue开发者工具
文章目录 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染2. 插值表达式{{}}3. 访问数据和修改数据4. vue响应式5. Vue开发者工具--方便调试 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染 准备容器引包创建Vue实例 new Vue()指定配置项 ->渲染数据 准备一个容器,例如: …...
