ubuntu 20使用kubeadm安装k8s 1.26
步骤
机器:4核8G,root账号,可访问互联网
1、更新apt apt-get update
2、安装一些基本工具 apt-get install ca-certificates curl gnupg lsb-release net-tools apt-transport-https
3、ifconfig 获取ip,hostname获取主机名,若主机名不符合规范(比如有特殊字符,则使用hostnamectl set-hostname <hostname>修改)
4、更新hosts echo "<ip> <hostname>" >> /etc/hosts
5、mkdir -m 0755 -p /etc/apt/keyrings
6、装证书curl -fsSL https://download.docker.com/linux/ubuntu/gpg | sudo gpg --dearmor -o /etc/apt/keyrings/docker.gpg
7、声明软件源echo "deb [arch=$(dpkg --print-architecture) signed-by=/etc/apt/keyrings/docker.gpg] https://download.docker.com/linux/ubuntu $(lsb_release -cs) stable" | sudo tee /etc/apt/sources.list.d/docker.list > /dev/null
7、更新aptapt-get update
8、安装docker和containerdapt-get install docker-ce docker-ce-cli containerd.io docker-buildx-plugin docker-compose-plugin
9、此时docker命令可用,crictl还不行
10、准备安装kubeadmcurl -fsSL https://mirrors.aliyun.com/kubernetes/apt/doc/apt-key.gpg | sudo gpg --dearmor -o /etc/apt/keyrings/k8s.gpg
11、echo "deb [arch=$(dpkg --print-architecture) signed-by=/etc/apt/keyrings/k8s.gpg] https://mirrors.aliyun.com/kubernetes/apt/ kubernetes-xenial main" | sudo tee /etc/apt/sources.list.d/kubernetes.list > /dev/null
12、更新aptapt-get update
13、安装kubeadm apt-get install -y kubelet=1.26.1-00 kubeadm=1.26.1-00 kubectl=1.26.1-00
14、apt-mark hold kubelet kubeadm kubectl
15、vi /etc/crictl.yaml 编辑crictl配置,文件内容如下:
runtime-endpoint: unix:///run/containerd/containerd.sock
image-endpoint: unix:///run/containerd/containerd.sock
timeout: 10
debug: false
16、containerd使用配置。containerd config default > /etc/containerd/config.toml
17、修改containerd默认配置:
sandbox_image = "registry.aliyuncs.com/google_containers/pause:3.9"
SystemdCgroup = true
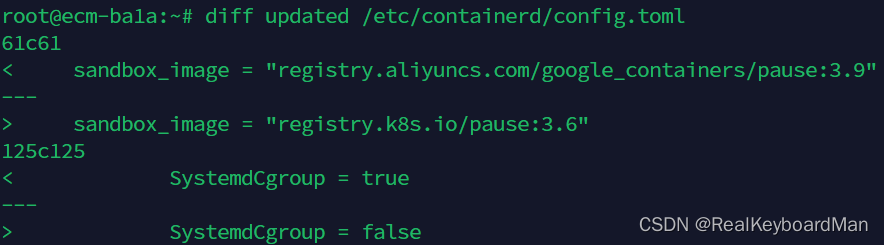
18、重启服务 systemctl restart containerd
19、禁用交换分区swapoff -a && sed -i 's/.*swap.*/#&/' /etc/fstab
20、编辑kubeadm启动文件,vi kubeadm.yaml
apiServer:timeoutForControlPlane: 4m0s
apiVersion: kubeadm.k8s.io/v1beta3
certificatesDir: /etc/kubernetes/pki
clusterName: kubernetes
controllerManager: {}
dns: {}
etcd:local:dataDir: /var/lib/etcd
imageRepository: registry.aliyuncs.com/google_containers
kind: ClusterConfiguration
kubernetesVersion: 1.26.0
networking:dnsDomain: cluster.localserviceSubnet: 10.96.0.0/12
scheduler: {}
21.启动kubeadmkubeadm init --config kubeadm.yaml
参考文档
1、安装docker和containerd:https://docs.docker.com/engine/install/ubuntu/
2、安装kubeadm:https://kubernetes.io/zh-cn/docs/setup/production-environment/tools/kubeadm/install-kubeadm/
相关文章:

ubuntu 20使用kubeadm安装k8s 1.26
步骤 机器:4核8G,root账号,可访问互联网 1、更新apt apt-get update 2、安装一些基本工具 apt-get install ca-certificates curl gnupg lsb-release net-tools apt-transport-https 3、ifconfig 获取ip,hostname获取主机名&…...

低代码开发平台|制造管理-生产过程管理搭建指南
1、简介1.1、案例简介本文将介绍,如何搭建制造管理-生产过程。1.2、应用场景先填充工序信息,再设置工艺路线对应的工序;工序信息及工艺路线列表报表展示的是所有工序、工艺路线信息,可进行新增对应数据的操作。2、设置方法2.1、表…...
python对多个csv文件进行合并(表头需一致)
之前写过python对【多个Excel文件】中的【单个sheet】进行合并,参考:点我 之前也写过python对【多个Excel文件】中的【多个sheet】进行合并,参考:点我 今天再写一个python对多个csv格式的文件进行合并的小工具 但是大家切记&am…...

Salesforce Apex调用邮件模板
正常调用无模板:mail.setToAddresses(new List<String>{user.Email});//mail.setReplyTo(444298824qq.com);//mail.setCcAddresses(null);mail.setSenderDisplayName(EOP系统);mail.setSubject(EOP通知(待审批):您有未处理的…...
windows本地开发Spark[不开虚拟机]
1. windows本地安装hadoop hadoop 官网下载 hadoop2.9.1版本 1.1 解压缩至C:\XX\XX\hadoop-2.9.1 1.2 下载动态链接库和工具库 1.3 将文件winutils.exe放在目录C:\XX\XX\hadoop-2.9.1\bin下 1.4 将文件hadoop.dll放在目录C:\XX\XX\hadoop-2.9.1\bin下 1.5 将文件hadoop.dl…...

一文教你快速估计个股交易成本
交易本身对市场会产生影响,尤其是短时间内大量交易,会影响金融资产的价格。一个订单到来时的市场价格和订单的执行价格通常会有差异,这个差异通常被称为交易成本。在量化交易的策略回测部分,不考虑交易成本或者交易成本估计不合理…...

Leetcode—移除元素、删除有序数组中的重复项、合并两个有序数组
移除元素 此题简单,用双指针方法即可, 如果右指针指向的元素不等于val,它一定是输出数组的一个元素,我们就将右指针指向的元素复制到左指针位置,然后将左右指针同时右移; 如果右指针指向的元素等于 val&…...
大疆 安全开发 C++1面)
面试(十)大疆 安全开发 C++1面
1. 在C++开发中定义一个变量,若不做初始化直接使用会怎样? 如果该变量是一个普通变量,则如果对其进行访问,会返回一个随机值,int类型不一定为0,bool类型也不一定为false 如果该变量为一个静态变量,则初始值都是一个0; 如果该变量是一个指针,那么在后续程序运行中很…...
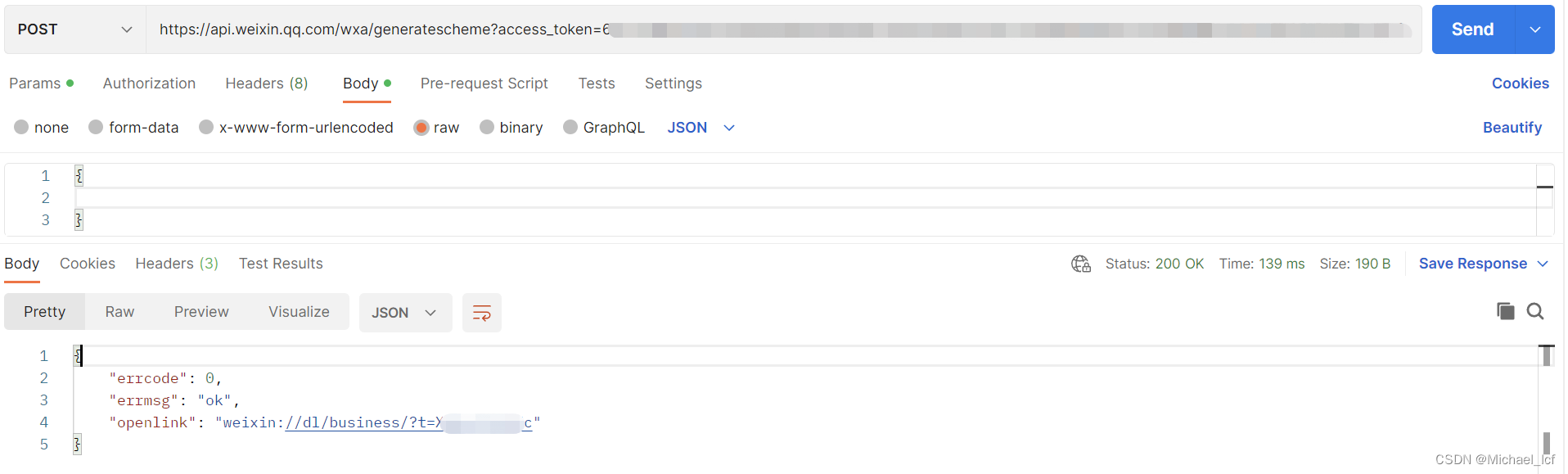
短信链接跳转微信小程序
短信链接跳转微信小程序1 实现方案1.1 通过URL Scheme实现1.2 通过URL Link实现1.3 通过云开发静态网站实现2 实现方案对比3 实践 URL Schema 方案3.1 获取微信access_token3.2 获取openlink3.3 H5页面(模拟短信跳转,验证ok)4 问题小节4.1 io…...

吉林电视台启用乾元通多卡聚合系统广电视频传输解决方案
随着广播电视数字化、IP化、智能化的逐步深入,吉林电视台对技术改造、数字设备升级提出了更高要求,通过对系统性能、设计理念的综合评估,正式启用乾元通多卡聚合系统广电视频传输解决方案,将用于大型集会、大型演出、基层直播活动…...
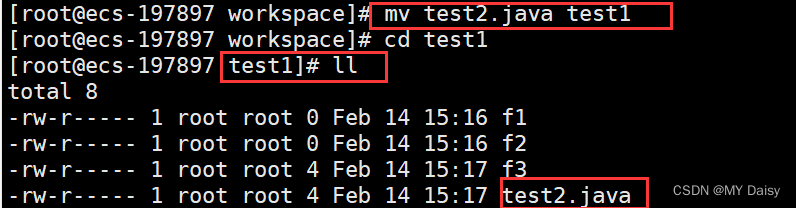
Linux常用命令1
目录1、远程登陆服务器2、文件相关(1)文件和目录属性(2)创建目录mkdir(3)删除目录rmdir(4)创建文件touch(5)删除文件或目录rm(6)ls命令…...

【C++进阶】一、继承(总)
目录 一、继承的概念及定义 1.1 继承概念 1.2 继承定义 1.3 继承基类成员访问方式的变化 二、基类和派生类对象赋值转换 三、继承中的作用域 四、派生类的默认成员函数 五、继承与友元 六、继承与静态成员 七、菱形继承及菱形虚拟继承 7.1 继承的分类 7.2 菱形虚拟…...
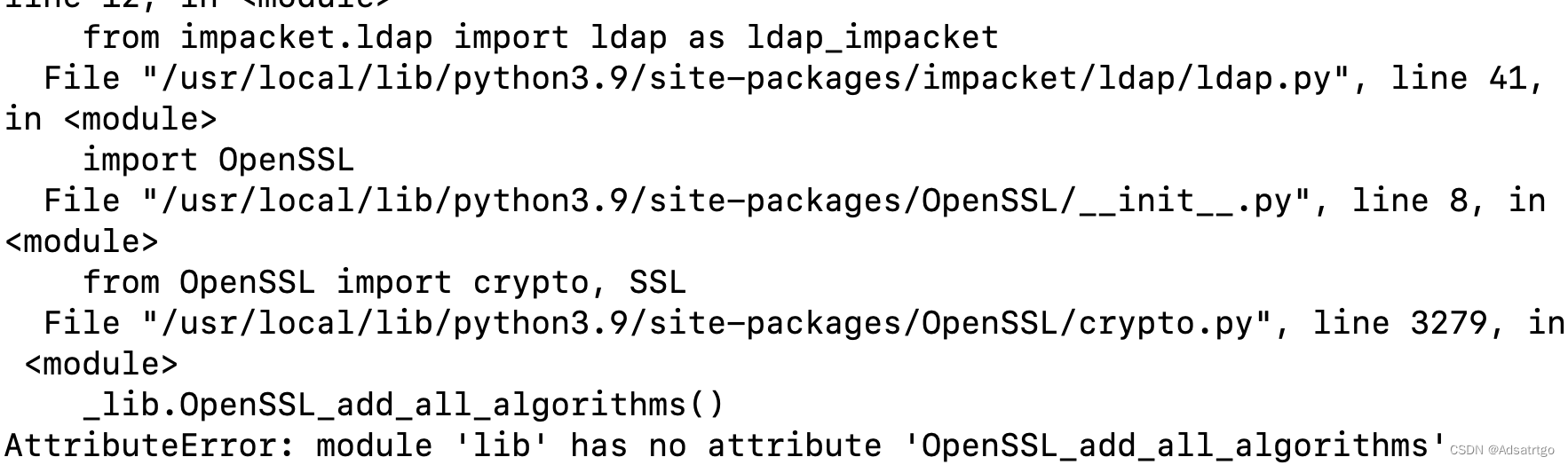
AttributeError: module ‘lib‘ has no attribute ‘OpenSSL_add_all_algorithms
pip安装crackmapexec后,运行crackmapexec 遇到报错 AttributeError: module lib has no attribute OpenSSL_add_all_algorithms 直接安装 pip3 install crackmapexec 解决 通过 python3 -m pip install --upgrade openssl 或者 python3 -m pip install openssl>22.1.…...

Python实现视频自动打码功能,避免看到羞羞的画面
前言 嗨呀嗨呀,最近重温了一档综艺节目 至于叫什么 这里就不细说了 老是看着看着就会看到一堆马赛克,由于太好奇了就找了一下原因,结果是因为某艺人塌房了…虽然但是 看综艺的时候满影响美观的 咳咳,这里我可不是来教你们如何解…...
说说Knife4j
Knife4j是一款基于Swagger2的在线API文档框架使用Knife4j, 需要 添加Knife4j的依赖当前建议使用的Knife4j版本, 只适用于Spring Boot2.6以下版本, 不含Spring Boot2.6 在主配置文件(application.yml)中开启Knife4j的增强模式必须在主配置文件中进行配置, 不要配置在个性化配置文…...
Java学习笔记-03(API阶段-2)集合
集合 我们接下来要学习的内容是Java基础中一个很重要的部分:集合 1. Collection接口 1.1 前言 Java语言的java.util包中提供了一些集合类,这些集合类又称之为容器 提到容器不难想到数组,集合类与数组最主要的不同之处是,数组的长度是固定的,集合的长度是可变的&a…...
)
「3」线性代数(期末复习)
🚀🚀🚀大家觉不错的话,就恳求大家点点关注,点点小爱心,指点指点🚀🚀🚀 矩阵的秩 定义4:在mxn矩阵A中,任取k行与k列(k<m,k<n),位…...
)
【CSDN竞赛】27期题解(Javascript)
前言 本来排名是20的,不过第一题有点输出bug,最后实际测出来又重新排名,刚好卡在第10。但是考试报告好像过了12小时就下载不到了,所以就只写题目求解的JS函数吧。 1. 幸运数字 小艺定义一个幸运数字的标准包含3条: 仅包含4或7幸…...

高压放大器在骨的逆力电研究中的应用
实验名称:高压放大器在骨的逆力电研究中的应用研究方向:生物医学测试目的:骨中的胶原和羟基磷灰石沿厚度分布不均匀,骨试样在直流电压作用下,内部出现传导电流引起试样内部温度升高,不同组分热变形不一致&a…...
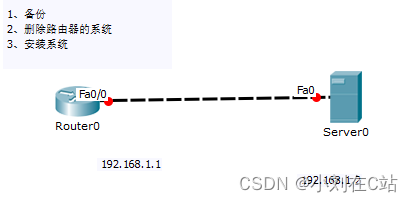
思科网络部署,(0基础)入门实验,超详细
♥️作者:小刘在C站 ♥️个人主页:小刘主页 ♥️每天分享云计算网络运维课堂笔记,努力不一定有收获,但一定会有收获加油!一起努力,共赴美好人生! ♥️夕阳下,是最美的绽放࿰…...

C++初阶-list的底层
目录 1.std::list实现的所有代码 2.list的简单介绍 2.1实现list的类 2.2_list_iterator的实现 2.2.1_list_iterator实现的原因和好处 2.2.2_list_iterator实现 2.3_list_node的实现 2.3.1. 避免递归的模板依赖 2.3.2. 内存布局一致性 2.3.3. 类型安全的替代方案 2.3.…...
:にする)
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする 1、前言(1)情况说明(2)工程师的信仰2、知识点(1) にする1,接续:名词+にする2,接续:疑问词+にする3,(A)は(B)にする。(2)復習:(1)复习句子(2)ために & ように(3)そう(4)にする3、…...

【Java学习笔记】Arrays类
Arrays 类 1. 导入包:import java.util.Arrays 2. 常用方法一览表 方法描述Arrays.toString()返回数组的字符串形式Arrays.sort()排序(自然排序和定制排序)Arrays.binarySearch()通过二分搜索法进行查找(前提:数组是…...

【大模型RAG】Docker 一键部署 Milvus 完整攻略
本文概要 Milvus 2.5 Stand-alone 版可通过 Docker 在几分钟内完成安装;只需暴露 19530(gRPC)与 9091(HTTP/WebUI)两个端口,即可让本地电脑通过 PyMilvus 或浏览器访问远程 Linux 服务器上的 Milvus。下面…...

五年级数学知识边界总结思考-下册
目录 一、背景二、过程1.观察物体小学五年级下册“观察物体”知识点详解:由来、作用与意义**一、知识点核心内容****二、知识点的由来:从生活实践到数学抽象****三、知识的作用:解决实际问题的工具****四、学习的意义:培养核心素养…...

Xen Server服务器释放磁盘空间
disk.sh #!/bin/bashcd /run/sr-mount/e54f0646-ae11-0457-b64f-eba4673b824c # 全部虚拟机物理磁盘文件存储 a$(ls -l | awk {print $NF} | cut -d. -f1) # 使用中的虚拟机物理磁盘文件 b$(xe vm-disk-list --multiple | grep uuid | awk {print $NF})printf "%s\n"…...

【7色560页】职场可视化逻辑图高级数据分析PPT模版
7种色调职场工作汇报PPT,橙蓝、黑红、红蓝、蓝橙灰、浅蓝、浅绿、深蓝七种色调模版 【7色560页】职场可视化逻辑图高级数据分析PPT模版:职场可视化逻辑图分析PPT模版https://pan.quark.cn/s/78aeabbd92d1...

从零开始了解数据采集(二十八)——制造业数字孪生
近年来,我国的工业领域正经历一场前所未有的数字化变革,从“双碳目标”到工业互联网平台的推广,国家政策和市场需求共同推动了制造业的升级。在这场变革中,数字孪生技术成为备受关注的关键工具,它不仅让企业“看见”设…...

链式法则中 复合函数的推导路径 多变量“信息传递路径”
非常好,我们将之前关于偏导数链式法则中不能“约掉”偏导符号的问题,统一使用 二重复合函数: z f ( u ( x , y ) , v ( x , y ) ) \boxed{z f(u(x,y),\ v(x,y))} zf(u(x,y), v(x,y)) 来全面说明。我们会展示其全微分形式(偏导…...

[拓扑优化] 1.概述
常见的拓扑优化方法有:均匀化法、变密度法、渐进结构优化法、水平集法、移动可变形组件法等。 常见的数值计算方法有:有限元法、有限差分法、边界元法、离散元法、无网格法、扩展有限元法、等几何分析等。 将上述数值计算方法与拓扑优化方法结合&#…...
