MUSIC算法仿真
MUSIC算法原理及仿真
- DOA波达方向估计
- MUSIC算法概述
- MUSIC算法原理
- MUSIC算法MATLB仿真
DOA波达方向估计
DOA(Direction Of Arrival)波达方向是指通过阵列信号处理来估计来波的方向,这里的信源可能是多个,角度也有多个。DOA技术主要有ARMA谱分析、最大似然法、熵谱分析法和特征分解法,特征分解法主要有MUSIC算法、ESPRIT算法WSF算法等。其中MUSIC是一种经典的DOA估计算法。
MUSIC算法概述
MUSIC(multiple signal classification algorithm)算法是一种基于矩阵特征空间分解的方法。从几何角度讲,信号处理的观测空间可以分解为信号子空间和噪声子空间,显然这两个空间是正交的。信号子空间由阵列接收到的数据协方差矩阵中与信号对应的特征向量组成,噪声子空间则由协方差矩阵中所有最小特征值(噪声方差)对应的特征向量组成。
MUSIC算法原理
MUSIC算法是空间谱估计测向理论的重要基石。算法原理 如下:
(1) 不管测向天线阵列形状如何,也不管入射来波入射角的维数如何,如图1所示,假定阵列由 N N N个阵元组成,并且符合窄带、远场模型。

则阵列输出模型的矩阵形式都可以表示为: Y ( t ) = A S + N ( t ) Y(t)=AS+N(t) Y(t)=AS+N(t)
其中, Y Y Y是观测到的阵列输出数据复向量; X X X是未知的空间信号复向量; N ( t ) N(t) N(t)是阵列输出向量中的加性噪声; A A A是阵列的方向矩阵,又称之为阵列流形矩阵;当我们以最左侧的阵元为参考位,此处, A A A矩阵表达式表示为:
A = [ α ( θ 1 ) , α ( θ 2 ) , ⋯ , α ( θ M ) ] = [ 1 1 ⋯ 1 e − j ϕ 1 e − j ϕ 2 ⋯ e − j ϕ D e j − 2 ϕ 1 e − j 2 ϕ 2 ⋯ e − j 2 ϕ D ⋮ ⋮ ⋱ ⋮ e − j ( N − 1 ) ϕ 1 e − j ( N − 1 ) ϕ 2 ⋯ e − j ( N − 1 ) ϕ D ] A=[\alpha(\theta_1),\alpha(\theta_2),\cdots,\alpha(\theta_M)]=\begin{equation} \begin{bmatrix} 1 & 1 & \cdots &1 \\ e^{-j\phi_1} & e^{-j\phi_2} & \cdots & e^{-j\phi_D} \\ e^{j-2\phi_1} & e^{-j2\phi_2} & \cdots & e^{-j2\phi_D} \\ \vdots & \vdots & \ddots & \vdots \\ e^{-j(N-1)\phi_1} & e^{-j(N-1)\phi_2} & \cdots & e^{-j(N-1)\phi_D} \end{bmatrix} \end{equation} A=[α(θ1),α(θ2),⋯,α(θM)]= 1e−jϕ1ej−2ϕ1⋮e−j(N−1)ϕ11e−jϕ2e−j2ϕ2⋮e−j(N−1)ϕ2⋯⋯⋯⋱⋯1e−jϕDe−j2ϕD⋮e−j(N−1)ϕD
可以看到, A A A是一个范德蒙矩阵其中, ϕ k = 2 π s i n θ k / λ \phi_k=2{\pi}sin\theta_k/\lambda ϕk=2πsinθk/λ,且 θ k , 1 ≤ k ≤ D \theta_k,1\le k \le D θk,1≤k≤D为第 k k k个信源的角度,共有 D D D个角度。 ϕ k \phi_k ϕk在这里是指波程差引起的相移,如下图所示相邻阵元之间的波程差为 d s i n θ dsin\theta dsinθ,将此转换为相位,单位为弧度,则为 2 π s i n θ k / λ 2{\pi}sin\theta_k/\lambda 2πsinθk/λ, λ \lambda λ为信号波长。由下图的等相位面可知,信号到达最左侧的阵元需要走更远的距离,因此,以最左侧的阵元为参考,即左侧阵元接收到的信号为 x 1 ( t ) x_1(t) x1(t),则其他阵元接收到的信号都滞后于它,此时, x 1 ( t ) = s ( t ) , x 2 ( t ) = s ( t ) e − j ϕ x_1(t)=s(t),x_2(t)=s(t)e^{-j\phi } x1(t)=s(t),x2(t)=s(t)e−jϕ。如果,我们以最右侧信号为参考,即最右侧阵元接收到的信号为 x 1 ( t ) x_1(t) x1(t),则 x 1 ( t ) = s ( t ) , x 2 ( t ) = s ( t ) e j ϕ x_1(t)=s(t),x_2(t)=s(t)e^{j\phi } x1(t)=s(t),x2(t)=s(t)ejϕ。注意角度的正负号。

接收信号写为向量形式:
Y ( t ) = [ y 1 ( t ) y 2 ( t ) y 3 ( t ) ⋮ y N ( t ) ] Y(t)=\begin{equation} \begin{bmatrix} y_1(t) \\ y_2(t) \\ y_3(t) \\ \vdots \\ y_N(t) \end{bmatrix} \end{equation} Y(t)= y1(t)y2(t)y3(t)⋮yN(t)
y i ( t ) y_i(t) yi(t)为第 i i i个阵元接收到的信号,共有 N N N个阵元。 S = [ s 1 ( t ) , s 2 ( t ) , ⋯ , s D ( t ) ] S=[s_1(t),s_2(t),\cdots,s_D(t)] S=[s1(t),s2(t),⋯,sD(t)], s i ( t ) , 1 ≤ i ≤ D s_i(t),1\le i \le D si(t),1≤i≤D,表示第 i i i个信源发出的信号。 N ( t ) = [ n 1 ( t ) , n 2 ( t ) , ⋯ , n N ( t ) ] T N(t)=[n_1(t),n_2(t),\cdots,n_N(t)]^T N(t)=[n1(t),n2(t),⋯,nN(t)]T,表示噪声,符合独立同分布的假设。
MUSIC算法的处理任务就是设法估计出入射到阵列的空间信号的个数 D D D以及空间信号源的强度及其来波方向 θ k \theta_k θk。
(2) 在实际处理中, Y Y Y得到的数据是有限时间段内的有限次数的样本(也称快拍或快摄),样本的长度取决于采样率和采样时间,在这段时间内,假定来波方向不发生变化,且噪声为与信号不相关的白噪声,则定义阵列输出信号的二阶矩: R y R_y Ry。
R y = E [ Y Y H ] R_y=E[YY^H] Ry=E[YYH]
其中, [ ∙ ] H [\bullet]^H [∙]H表示共轭转置,值得注意的是,在MATLAB中我们常用的转置符号(‘)其实是共轭转置,而普通转置为(.'),当然他们对于实数矩阵而言没有任何区别。 E [ ∙ ] E[\bullet] E[∙]表示统计学上的期望。
由于噪声信号符合独立同分布的假设,信号与噪声互不相关,噪声为零均值白噪声,则上式又可以写为:
R y = E [ Y Y H ] = E [ ( A S + N ) ( A S + N ) H ] = A E [ S S H ] A H + E [ N N H ] = A R S A H + R N R_y=E[YY^H]=E[(AS+N)(AS+N)^H]=AE[SS^H]A^H+E[NN^H]=AR_SA^H+R_N Ry=E[YYH]=E[(AS+N)(AS+N)H]=AE[SSH]AH+E[NNH]=ARSAH+RN
其中, R S = E [ S S H ] R_S=E[SS^H] RS=E[SSH]为信号相关矩阵, R N = E [ N N H ] = σ 2 I R_N=E[NN^H]=\sigma^2I RN=E[NNH]=σ2I为噪声相关矩阵, I I I为 N ∗ N N^*N N∗N的单位矩阵。
(3) MUSIC算法的核心就是对 R y R_y Ry进行特征值分解,利用特征向量构建两个正交的子空间,即信号子空间和噪声子空间。对 R y R_y Ry进行特征分解。
(4) U U U是非负定的厄米特矩阵,所以特征分解得到的特征值均为非负实数,有 D D D个大的特征值和 M − D M-D M−D个小的特征值,大特征值对应的特征向量组成的空间Us为信号子空间,小特征值对应的特征向量组成的空间 U n U_n Un为噪声子空间。
(5) 将噪声特征向量作为列向量,组成噪声特征矩阵 ,并张成 M − D M-D M−D维的噪声子空间 U n U_n Un,噪声子空间与信号子空间正交。而 U s U_s Us的列空间向量恰与信号子空间重合,所以 U s U_s Us的列向量与噪声子空间也是正交的,由此,可以构造空间谱函数。
(6) 在空间谱域求取谱函数最大值,其谱峰对应的角度即是来波方向角的估计值。
P m u s i c = 1 α H ( θ ) U n U n H α ( θ ) P_{music}=\frac{1}{\alpha^H(\theta)U_nU^H_n\alpha(\theta)} Pmusic=αH(θ)UnUnHα(θ)1
MUSIC算法MATLB仿真
% MUSIC空间谱估计算法仿真
close all; clear all; clc;
J=sqrt(-1);
source_number=4;
source_doa=[30 40 50 70];
sensor_number=7;
snapshot_number=2000;
snr=10; A=exp(-J*(0:sensor_number-1)'*pi*sin(source_doa*pi/180));
s=(randn(source_number,snapshot_number)+J*randn(source_number,snapshot_number))/sqrt(2);
x=A*s;
y=awgn(x,snr,'measured');
R=y*y'/snapshot_number;
[V,D]=eig(R);
Un=V(:,1:sensor_number-source_number);
Gn=Un*Un'; searching_doa=0:0.1:90;
for i=1:length(searching_doa) a_theta=exp(-J*(0:sensor_number-1)'*pi*sin(pi*searching_doa(i)/180))P_con(i)=abs(a_theta'*R*a_theta);P_BF(i)=abs((a_theta'*R*a_theta)./(a_theta'*a_theta)); P_capon(i)=1./abs((a_theta'*inv(R)*a_theta)); P_music(i)=1./abs((a_theta'*Gn*a_theta));
end
plot(searching_doa,P_con/max(P_con),'k');hold on;
plot(searching_doa,P_BF/max(P_BF),'r'); hold on;
plot(searching_doa,P_capon/max(P_capon),'g'); hold on;
plot(searching_doa,P_music/max(P_music),'b'); hold off;grid on;
xlabel('ang');
ylabel('功率谱估计');
legend('conditional spectrum','Bartlett spectrum','Capon spectrum','Music spectrum');
仿真结果如下:

还有一种参考程序:
clear; close all;
%%%%%%%% MUSIC for Uniform Linear Array%%%%%%%%
derad = pi/180; %角度->弧度
N = 8; % 阵元个数
M = 3; % 信源数目
theta = [-30 0 60]; % 待估计角度
snr = 10; % 信噪比
K = 512; % 快拍数dd = 0.5; % 阵元间距
d=0:dd:(N-1)*dd;
A=exp(-1i*2*pi*d.'*sin(theta*derad)); %方向矢量%%%%构建信号模型%%%%%
S=randn(M,K); %信源信号,入射信号
X=A*S; %构造接收信号
X1=awgn(X,snr,'measured'); %将白色高斯噪声添加到信号中
% 计算协方差矩阵
Rxx=X1*X1'/K;
% 特征值分解
[EV,D]=eig(Rxx); %特征值分解
EVA=diag(D)'; %将特征值矩阵对角线提取并转为一行
[EVA,I]=sort(EVA); %将特征值排序 从小到大
EV=fliplr(EV(:,I)); % 对应特征矢量排序% 遍历每个角度,计算空间谱
for iang = 1:361angle(iang)=(iang-181)/2;phim=derad*angle(iang);a=exp(-1i*2*pi*d*sin(phim)).'; En=EV(:,M+1:N); % 取矩阵的第M+1到N列组成噪声子空间Pmusic(iang)=1/(a'*En*En'*a);
end
Pmusic=abs(Pmusic);
Pmmax=max(Pmusic)
Pmusic=10*log10(Pmusic/Pmmax); % 归一化处理
h=plot(angle,Pmusic);
set(h,'Linewidth',2);
xlabel('入射角/(degree)');
ylabel('空间谱/(dB)');
set(gca, 'XTick',[-90:30:90]);
grid on;
仿真结果如下:

相关文章:

MUSIC算法仿真
MUSIC算法原理及仿真 DOA波达方向估计MUSIC算法概述MUSIC算法原理MUSIC算法MATLB仿真 DOA波达方向估计 DOA(Direction Of Arrival)波达方向是指通过阵列信号处理来估计来波的方向,这里的信源可能是多个,角度也有多个。DOA技术主要…...

redis 数据类型详解 以及 redis适用场景场合
1. MySqlMemcached架构的问题 实际MySQL是适合进行海量数据存储的,通过Memcached将热点数据加载到cache,加速访问,很多公司都曾经使用过这样的架构,但随着业务数据量的不断增加,和访问量的持续增长,我们遇…...

python基于轻量级YOLOv5的生猪检测+状态识别分析系统
在我之前的一篇文章中有过生猪检测盒状态识别相关的项目实践,如下: 《Python基于yolov4实现生猪检测及状态识》 感兴趣的话可以自行移步阅读,这里主要是基于同样的技术思想,将原始体积较大的yolov4模型做无缝替换,使…...

阅读笔记 First Order Motion Model for Image Animation
文章解决的是图片动画的问题。假设有源图片和驱动视频,并且其中的物体是同一类的,文章的方法让源图片中的物体按照驱动视频中物体的动作而动。 文章的方法只需要一个同类物体的视频集,不需要而外的标注。 方法 该方法基于self-supervised策…...
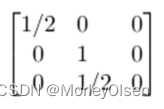
【计算机图形学】课堂习题汇总
在直线的光栅化算法中,如果不考虑最大位移方向则可能得到怎样的直线? A:斜率为1的线 B:总是垂直的 C:离散的点,无法构成直线 D:总是水平的 在直线的改进的Bresenham算法中,每当误…...

国外导师对博士后申请简历的几点建议
正所谓“工欲善其事,必先利其器”,想要申请国外的博士后职位,就要准备好相应的申请文书材料。如果说Cover Letter是职位的窍门砖,那么申请者的简历就是争取职位的决定性筹码。 相信大家已经看过许多简历的模版了,但是…...

【五一创作】Scratch资料袋
Scratch软件是免费的、免费的、免费的。任何需要花钱才能下载Scratch软件的全是骗子。 1、什么是Scratch Scratch是麻省理工学院的“终身幼儿园团队”开发的一种图形化编程工具。是面向青少年的一款模块化,积木化、可视化的编程语言。 什么是模块化、积木化&…...
数据库基础篇 《17.触发器》
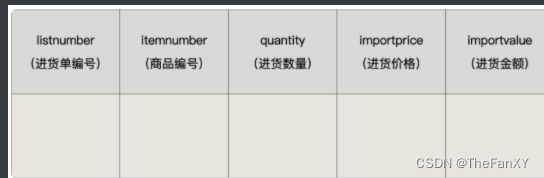
数据库基础篇 《17.触发器》 在实际开发中,我们经常会遇到这样的情况:有 2 个或者多个相互关联的表,如商品信息和库存信息分别存放在 2 个不同的数据表中,我们在添加一条新商品记录的时候,为了保证数据的完整性&#…...

03 - 大学生如何使用GPT
大学生如何使用GPT提高学习效率 一、引言 在当今的高速发展的信息时代,大学生面临着越来越多的学习挑战。作为一种先进的人工智能技术,GPT为大学生提供了一种强大的学习工具。本文将介绍大学生在不同场景中如何使用GPT来提高学习效率,并给出…...

【P1】Jmeter 准备工作
文章目录 一、Jmeter 介绍1.1、Jmeter 有什么样功能1.2、Jmeter 与 LoadRunner 比较1.3、常用性能测试工具1.4、性能测试工具如何选型1.5、学习 Jmeter 对 Java 编程的要求 二、Jmeter 软件安装2.1、官网介绍2.2、JDK 安装及环境配置2.3、Jmeter 三种模式2.4、主要配置介绍2.4.…...
字节的面试,你能扛住几道?
C , Python 哪一个更快? 读者答:这个我不知道从哪方面说,就是 C 的话,它其实能够提供开发者非常多的权限,就是说它能涉及到一些操作系统级别的一些操作,速度应该挺快。然后 Python 实现功能还…...
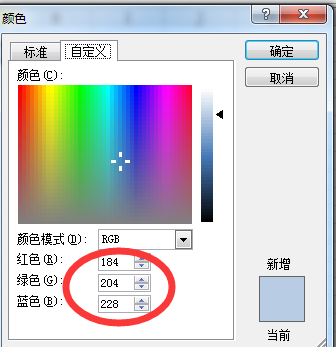
NOPI用法之自定义单元格背景色(3)
NPOI针对office2003使用HSSFWorkbook,对于offce2007及以上使用XSSFWorkbook;今天我以HSSFWorkbook自定义颜色为例说明,Office2007的未研究呢 在NPOI中默认的颜色类是HSSFColor,它内置的颜色有几十种供我们选择,如果不…...
数据分析中常见标准的参考文献
做数据分析过程中,有些分析法方法的标准随便一搜就能找到,不管是口口相传还是默认,大家都按那样的标准做了。日常分析不细究出处还可以,但是正式的学术论文你需要为你写下的每一句话负责,每一个判断标准都应该有参考文…...
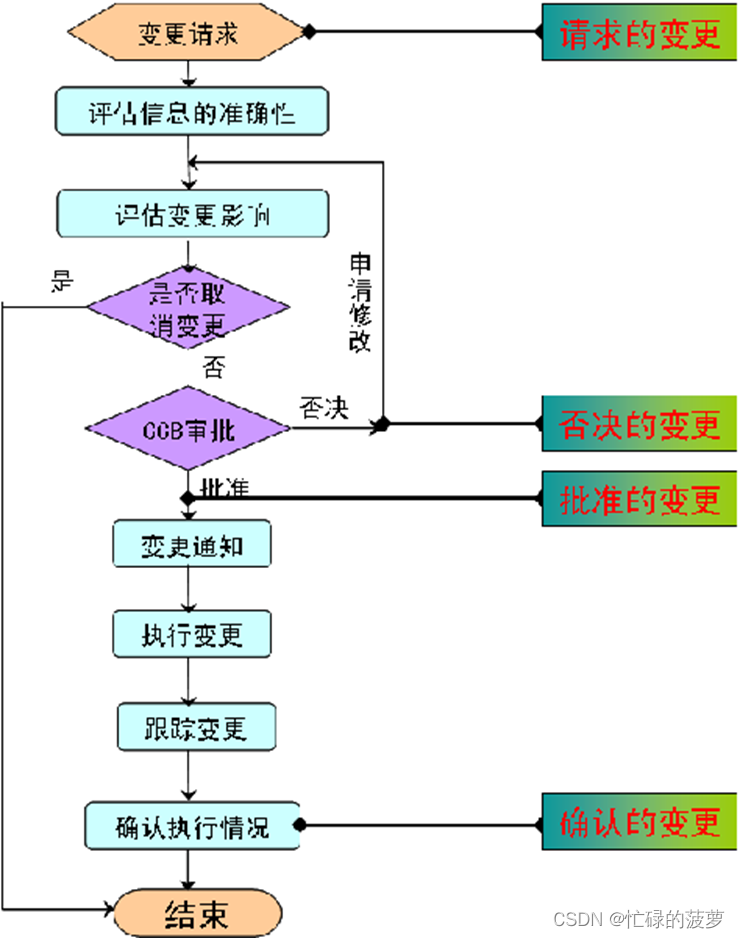
辨析 变更请求、批准的变更请求、实施批准的变更请求
变更请求、批准的变更请求、实施批准的变更请求辨析 辨析各种变更请求,不服来辨。 变更请求 定义:对正规受控的文件或计划(范围、进度、成本、政策、过程、计划或程序)等的变更,以反映修改或增加的意见或内容 根据变更请求的工作内容可将变…...

leetcode 561. 数组拆分
题目描述解题思路执行结果 leetcode 561. 数组拆分 题目描述 数组拆分 给定长度为 2n 的整数数组 nums ,你的任务是将这些数分成 n 对, 例如 (a1, b1), (a2, b2), ..., (an, bn) ,使得从 1 到 n 的 min(ai, bi) 总和最大。 返回该 最大总和 。 示例 1&am…...

AviatorScript
AviatorScript 是一门高性能、轻量级寄宿于 JVM (包括 Android 平台)之上的脚本语言 特性介绍 支持数字、字符串、正则表达式、布尔值、正则表达式等基本类型,完整支持所有 Java 运算符及优先级等。函数是一等公民,支持闭包和函…...
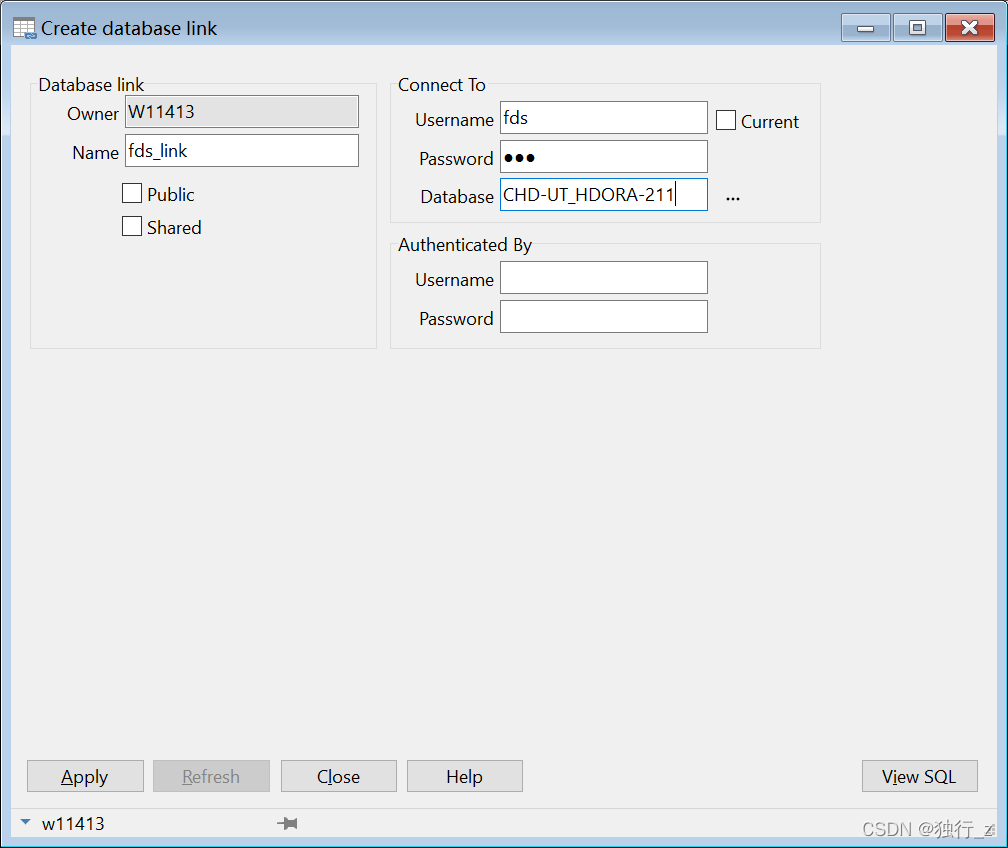
Oracle跨服务器取数——DBlink 初级使用
前言 一句话解释DBlink是干啥用的 实现跨库访问的可能性. 通过DBlink我们可以在A数据库访问到B数据库中的所有信息,例如我们在加工FDS层表时需要访问ODS层的表,这是就需要跨库访问 一、DBlink的分类 private:用户级别,只有创建该dblink的用户才可以使…...
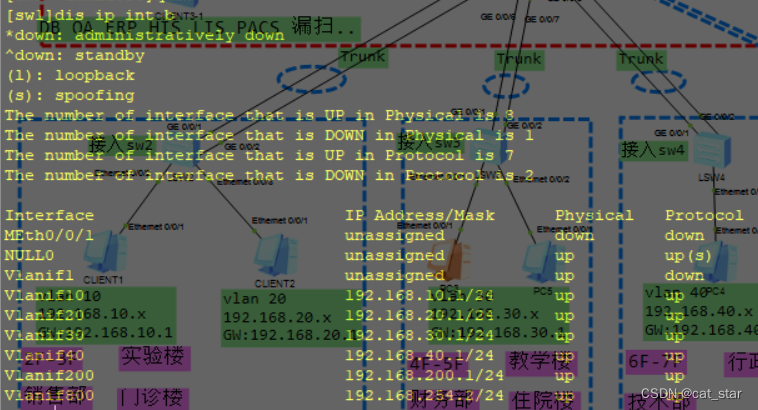
200人 500人 园区网设计
实验要求: ① 设置合理的STP优先级、边缘端口、Eth-trunk ② 企业内网划分多个vlan ,减少广播域大小,提高网络稳定性 ③ 所有设备,在任何位置都可以telnet远程管理 ④ 出口配置NAT ⑤ 所有用户均为自动获取ip地址 ⑥ 在企业…...
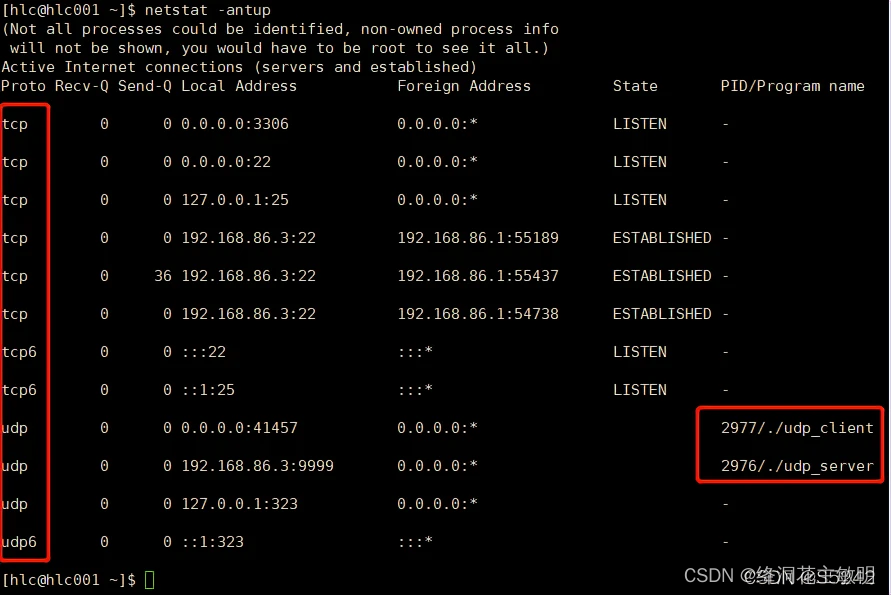
netstat命令解析
一、linux系统中netstat命令的帮助信息 └──╼ $netstat -h usage: netstat [-vWeenNcCF] [<Af>] -r netstat {-V|--version|-h|--help}netstat [-vWnNcaeol] [<Socket> ...]netstat { [-vWeenNac] -i | [-cnNe] -M | -s [-6tuw] }-r, --route …...

API接口的自我阐述
API(Application Programming Interface),翻译为应用程序接口,是一套定义程序之间如何通讯的接口。API可以实现软件的可重用性、可维护性和互操作性,同时也可以提升软件的性能和安全性。API接口是一个软件系统中的重要…...

C++:std::is_convertible
C++标志库中提供is_convertible,可以测试一种类型是否可以转换为另一只类型: template <class From, class To> struct is_convertible; 使用举例: #include <iostream> #include <string>using namespace std;struct A { }; struct B : A { };int main…...

AI Agent与Agentic AI:原理、应用、挑战与未来展望
文章目录 一、引言二、AI Agent与Agentic AI的兴起2.1 技术契机与生态成熟2.2 Agent的定义与特征2.3 Agent的发展历程 三、AI Agent的核心技术栈解密3.1 感知模块代码示例:使用Python和OpenCV进行图像识别 3.2 认知与决策模块代码示例:使用OpenAI GPT-3进…...

练习(含atoi的模拟实现,自定义类型等练习)
一、结构体大小的计算及位段 (结构体大小计算及位段 详解请看:自定义类型:结构体进阶-CSDN博客) 1.在32位系统环境,编译选项为4字节对齐,那么sizeof(A)和sizeof(B)是多少? #pragma pack(4)st…...

线程同步:确保多线程程序的安全与高效!
全文目录: 开篇语前序前言第一部分:线程同步的概念与问题1.1 线程同步的概念1.2 线程同步的问题1.3 线程同步的解决方案 第二部分:synchronized关键字的使用2.1 使用 synchronized修饰方法2.2 使用 synchronized修饰代码块 第三部分ÿ…...

linux 下常用变更-8
1、删除普通用户 查询用户初始UID和GIDls -l /home/ ###家目录中查看UID cat /etc/group ###此文件查看GID删除用户1.编辑文件 /etc/passwd 找到对应的行,YW343:x:0:0::/home/YW343:/bin/bash 2.将标红的位置修改为用户对应初始UID和GID: YW3…...

拉力测试cuda pytorch 把 4070显卡拉满
import torch import timedef stress_test_gpu(matrix_size16384, duration300):"""对GPU进行压力测试,通过持续的矩阵乘法来最大化GPU利用率参数:matrix_size: 矩阵维度大小,增大可提高计算复杂度duration: 测试持续时间(秒&…...

selenium学习实战【Python爬虫】
selenium学习实战【Python爬虫】 文章目录 selenium学习实战【Python爬虫】一、声明二、学习目标三、安装依赖3.1 安装selenium库3.2 安装浏览器驱动3.2.1 查看Edge版本3.2.2 驱动安装 四、代码讲解4.1 配置浏览器4.2 加载更多4.3 寻找内容4.4 完整代码 五、报告文件爬取5.1 提…...

STM32---外部32.768K晶振(LSE)无法起振问题
晶振是否起振主要就检查两个1、晶振与MCU是否兼容;2、晶振的负载电容是否匹配 目录 一、判断晶振与MCU是否兼容 二、判断负载电容是否匹配 1. 晶振负载电容(CL)与匹配电容(CL1、CL2)的关系 2. 如何选择 CL1 和 CL…...

抽象类和接口(全)
一、抽象类 1.概念:如果⼀个类中没有包含⾜够的信息来描绘⼀个具体的对象,这样的类就是抽象类。 像是没有实际⼯作的⽅法,我们可以把它设计成⼀个抽象⽅法,包含抽象⽅法的类我们称为抽象类。 2.语法 在Java中,⼀个类如果被 abs…...

git: early EOF
macOS报错: Initialized empty Git repository in /usr/local/Homebrew/Library/Taps/homebrew/homebrew-core/.git/ remote: Enumerating objects: 2691797, done. remote: Counting objects: 100% (1760/1760), done. remote: Compressing objects: 100% (636/636…...
