机器人中的数值优化(三)—— 无约束最优化方法基础、线搜索准则
本系列文章主要是我在学习《数值优化》过程中的一些笔记和相关思考,主要的学习资料是深蓝学院的课程《机器人中的数值优化》和高立编著的《数值最优化方法》等,本系列文章篇数较多,不定期更新,上半部分介绍无约束优化,下半部分介绍带约束的优化,中间会穿插一些路径规划方面的应用实例
四、无约束最优化方法基础
1、无约束的最优化问题描述
无约束的最优化问题可以描述成,求取使得目标函数值最小的最优解 x ∗ x^{*} x∗,即:
min f ( x ) \min f(x) minf(x)
其中:

注1:最优解 x ∗ x^{*} x∗,是一个解集,可能包含一个解、多个解,也有可能不存在
2、函数下降方向d
内容补充:设 x k x_k xk 是经 k 步迭代后得到的迭代点, d k d_k dk 是在 x k x_k xk 点使 f ( x ) f(x) f(x) 下降的方向, a k a_k ak > 0 是沿 d k d_k dk 的步长,第k+1个选代点则可用下式表示,它满足 f ( x k + 1 ) < f ( x k ) . f\left(x_{k+1}\right)<f\left(x_{k}\right). f(xk+1)<f(xk).
x k + 1 = x k + α k d k x_{k+1}=x_{k}+\alpha_{k}d_{k} xk+1=xk+αkdk
那么我们来思考满足什么条件的方向是在 x k x_k xk 点使 f ( x ) f(x) f(x) 下降的方向呢?
对任意 d ∈ R n d ∈R^n d∈Rn,若存在 α ‾ k \overline{\alpha}_{k} αk,使 f ( x k + α d ) < f ( x k ) , ∀ α ∈ ( 0 , α ˉ k ) f\left(x_{k}+\alpha d\right)<f\left(x_{k}\right),\forall\alpha\in\left(0,\bar{\alpha}_{k}\right) f(xk+αd)<f(xk),∀α∈(0,αˉk),则d为 f ( x ) f(x) f(x) 在点 x k x_k xk 处下降的方向,将 f ( x k + α d ) f\left(x_{k}+\alpha d\right) f(xk+αd)在点 x k x_k xk 处泰勒展开得到下式:
f ( x k + α d ) = f ( x k ) + α ∇ f ( x ) T d + O ( ∥ α d ∥ 2 ) f\left(x_{k}+\alpha d\right)=f\left(x_{k}\right)+\alpha \nabla f\left(x\right)\text{}^{\text{T}}d+O\left(\left\|\alpha d\right\|^{2}\right) f(xk+αd)=f(xk)+α∇f(x)Td+O(∥αd∥2)
由上式可知,当下降方向d满足 g k T d < 0 g_{k}^{T}d<0 gkTd<0时,d即为使得 f ( x ) f(x) f(x) 在点 x k x_k xk 处下降的方向。
3、无约束最优化算法的基本结构及构成要素
第1步:给定初始点 x 0 ∈ R n , k : = 0 ; x_{0}\in{R}^{n},k:=0; x0∈Rn,k:=0;
第2步:若在 x k x_k xk点终止准则满足,则输出有关信息,停止迭代;
第3步:确定 f ( x ) f(x) f(x)在 x k x_k xk点的下降方向 d k d_k dk;
第4步:确定步长 a k a_k ak,使 f ( x k + α k d k ) f\left(x_{k}+\alpha_{k}d_{k}\right) f(xk+αkdk)较之 f ( x ) f(x) f(x)有某种意义的下降
第5步:令 x k + 1 : = x k + α k d k , k : = k + 1 x_{k+1}:=x_{k}+\alpha_{k}d_{k},k:=k+1 xk+1:=xk+αkdk,k:=k+1,转到第2步
构成一个最优化方法的基本要素有二:其一是下降的方向;其二是步长.也就是说不同的方法可得到不同的下降方向和步长。我们称所有具有以上结构的最优化方法为 线搜索(型)方法
在最优化方法中,下降的方向与步长的选取顺序不同,导致产生不同类型的方法.线搜索方法是在 x k x_k xk点求得下降方向 d k d_k dk,再沿 d k d_k dk确定步长 a k a_k ak;信赖域方法是先限定步长的范围,再同时确定下降方向 d k d_k dk和步长 a k a_k ak
算法的另一个重要问题是迭代的终止准则,因为局部极小点 x ∗ x^* x∗是稳定点,我们可用 ∥ ∇ f ( x k ) ∥ ⩽ ε \|\nabla\text{}f\left(x_k\right)\|\leqslant\varepsilon ∥∇f(xk)∥⩽ε 作为终止准则.这样对于使用者来说,就存在着一个选择 ε \varepsilon ε的问题. ε \varepsilon ε的大小决定所得迭代点 x k x_k xk近似 x ∗ x^* x∗的精度.上述准则有一定的局限性.例如,对于在极小点邻域内比较陡峭的函数,即使该邻域中的点已相当接近极小点,但其梯度值可能仍然较大,从而使迭代难以停止。
其他终止准则有 ∥ x k − x k ˉ + 1 ∥ ⩽ ε \|x_k-x_{\bar{k}+1}\|\leqslant\varepsilon ∥xk−xkˉ+1∥⩽ε 或者 f k − f k + 1 ⩽ ε f_k-f_{k+1}\leqslant\varepsilon fk−fk+1⩽ε等,这两个准则满足只能说明算法这时所进行的迭代对迭代点或迭代点处目标函数值的改善已经很小,并不能保证 ∥ x k − x ∗ ∥ \|x_k-x^*\| ∥xk−x∗∥ 或者 f k − f ⋆ f_k-f^{\star} fk−f⋆一定足够小。
五、线搜索准则
在当前迭代点 x k x_k xk ,假定我们已得到下降方向 d k d_k dk ,求步长 a k a_k ak的问题为一维搜索或线搜索问题,它包括两个内容:满足什么样的准则,步长可以接受?有了合适的准则,满足该准则的步长该如何求?
对如何确定 a k a_k ak的接受准则这个问题,有两个最简单、直观的方法。即精确线搜索和非精确线搜索
(1)精确线搜索准则
精确线搜索是优化算法中一种用于确定每一步迭代中最优步长的方法。该方法的目标是在给定的搜索方向上找到能够最小化目标函数的步长,从而快速收敛到最优解。它通常应用于梯度下降法和共轭梯度法等优化算法中。
精确线搜索即使 f ( x ) f(x) f(x)沿着 d k d_k dk寻找一个步长 a a a使得函数在该点处取得极小值,如下式所示:
min α f ( x k + α d k ) \min\limits_\alpha f(x_k+\alpha d_k) αminf(xk+αdk)
设上式的解为 a k a_k ak,则 x k + 1 x_{k+1} xk+1= x k x_{k} xk+ a k a_{k} ak d k d_{k} dk且 ∇ f ( x k ) T d k = 0 \nabla f\left(x_{k}\right)^\mathrm{T}d_k=0 ∇f(xk)Tdk=0
这一点对一些无约束最优化方法的有限终止起着关键作用.然而,做精确线搜索需要求几乎精确的步长因子,当n 非常大或 f ( x ) f(x) f(x)非常复杂时,精确线搜索的计算量是相当大的,.实际上,当迭代点离最优解尚远时,是没有必要做高精度线搜索的.另外,对一般问题而言,实现精确线搜索是很困难的。
(2)非精确线搜索准则
正是因为精确线搜索存在的这些问题,我们产生了做非精确线搜索的想法.对于步长的选取准则,我们会自然地产生第二个简单的想法,即取 a k a_{k} ak,使其满足如下表达式
f ( x k + α k d k ) < f ( x k ) f(x_k+\alpha_k d_k)<f(x_k) f(xk+αkdk)<f(xk)
在下图所示的例子中满足上式表达式的a取值范围为 ( 0 , β 1 )、 (0,β_1)、 (0,β1)、 ( β 2 , β 3 ) (β_2,β_3) (β2,β3),因此,仅通过以上表达式的准则来确定a的取值范围,得到的a可能会接近与区间 ( 0 , β 1 ) (0,β_1) (0,β1)的左端点0或者区间 ( β 2 , β 3 ) (β_2,β_3) (β2,β3)的右端点 β 3 β_3 β3,因此,我们应该增加一些新的准则来使得获取的a不太接近区间 ( 0 , β 1 ) (0,β_1) (0,β1)的左端点或者区间 ( β 2 , β 3 ) (β_2,β_3) (β2,β3)的右端点。

常用的准则有 Armijo 准则、Goldstein 准则、Wolfe 准则、强Wolfe 准则等,些常用的准则.这些准则都是建立在 f ( x k + α k d k ) f(x_k+\alpha_k d_k) f(xk+αkdk)在零点处的斜率 ∇ f ( x k ) T d k \nabla f\left(x_{k}\right)^\mathrm{T}d_k ∇f(xk)Tdk为负值的前提上,否则,说明 d k d_k dk不是下降方向,不应被采用
① Armijo 准则
f ( x k + α d k ) ⩽ f ( x k ) + ρ ∇ f ( x k ) T d k α , ρ ∈ ( 0 , 1 ) . f(x_k+\alpha d_k)\leqslant f(x_k)+\rho \nabla f\left(x_{k}\right)^{\mathrm T}d_k\alpha,\quad\rho\in(0,1). f(xk+αdk)⩽f(xk)+ρ∇f(xk)Tdkα,ρ∈(0,1).
一般地,可取 ρ \rho ρ为 1 0 − 3 10^{-3} 10−3或更小的值,上式的右边是一个关于a的线性函数,由于 d k d_k dk是下降方向,满足 ∇ f ( x k ) T d k \nabla f\left(x_{k}\right)^\mathrm{T}d_k ∇f(xk)Tdk<0,该函数是关于a的减函数. 只要 a不取得太小,这个不等式可以保证新迭代点 x k + α d k x_k+\alpha d_k xk+αdk的函数值较之点 a k a_k ak的函数值有一定量的下降.满足该条件的点下图所示区间 ( 0 , β 4 ] (0,β_4] (0,β4]和 [ β 5 , β 6 ] [β_5,β_6] [β5,β6]中的点。
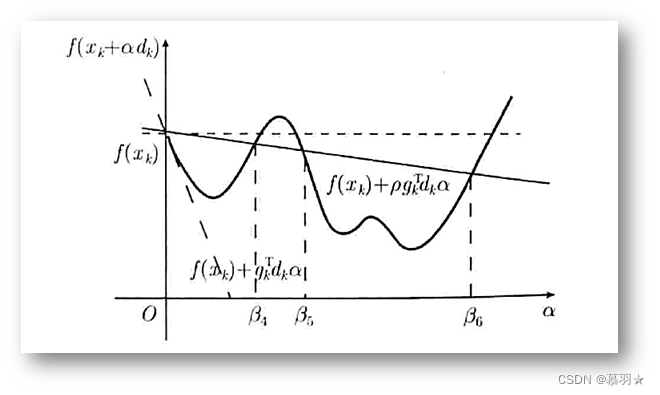
Armijo 准则可以避免α取得太大而接近于仅使用 f ( x k + α k d k ) < f ( x k ) f(x_k+\alpha_k d_k)<f(x_k) f(xk+αkdk)<f(xk)准则时图中的右端点的值.
有几种方法可以避免α取得太小而接近于仅使用 f ( x k + α k d k ) < f ( x k ) f(x_k+\alpha_k d_k)<f(x_k) f(xk+αkdk)<f(xk)准则时图中左端点的值,它们分别与Armijo 准则结合,构成如下准则
② Goldstein准则
f ( x k + α d k ) ⩽ f ( x k ) + ρ ∇ f ( x k ) T d k α , f ( x k + α d k ) ⩾ f ( x k ) + ( 1 − ρ ) ∇ f ( x k ) T d k α , \begin{array}{l}f(x_k+\alpha d_k)\leqslant f(x_k)+\rho \nabla f\left(x_{k}\right)^\mathrm{T}d_k\alpha,\\ f(x_k+\alpha d_k)\geqslant f(x_k)+(1-\rho)\nabla f\left(x_{k}\right)^\mathrm{T}d_k\alpha,\end{array} f(xk+αdk)⩽f(xk)+ρ∇f(xk)Tdkα,f(xk+αdk)⩾f(xk)+(1−ρ)∇f(xk)Tdkα,
其中ρ ∈(0,1/2),满足Goldstein准则的点是下图所示 ( β 7 , β 4 ] (β_7,β_4] (β7,β4]和 [ β 5 , β 6 ] [β_5,β_6] [β5,β6]中的点区间中的点。

Goldstein 准则是 Armijo 准则的改进版,增加了一个上限条件,限制步长不能太小,Goldstein准则可以避免α取得太大而接近于右端点的值,又可避免取得太小而接近于左端点的值。
③ Wolfe准则
f ( x k + α d k ) ⩽ f ( x k ) + ρ ∇ f ( x k ) T d k α , ∇ f ( x k + α d k ) T d k ⩾ σ ∇ f ( x k ) T d k , \begin{array}{l}f(x_k+\alpha d_k)\leqslant f(x_k)+\rho\nabla f\left(x_{k}\right)^\mathrm{T}d_k\alpha,\\ \nabla f(x_k+\alpha d_k)^{\mathrm T}d_k\geqslant\sigma \nabla f\left(x_{k}\right)^\mathrm{T}d_k,\end{array} f(xk+αdk)⩽f(xk)+ρ∇f(xk)Tdkα,∇f(xk+αdk)Tdk⩾σ∇f(xk)Tdk,
其中的σ和ρ满足1>σ >ρ>0,满足Wolfe 准则的点为下图所示区间 ( β 7 , β 4 ] (β_7,β_4] (β7,β4], [ β 8 , β 9 ] [β_8,β_9] [β8,β9], [ β 10 , β 6 ] [β_{10},β_6] [β10,β6]中的点.

Wolfe准则中的第二条是要求 f ( x k + α d k ) f(x_k+\alpha d_k) f(xk+αdk)在点a的斜率不能小于 f ( x k + α d k ) f(x_k+\alpha d_k) f(xk+αdk)在零点斜率 ∇ f ( x k ) T d k \nabla f\left(x_{k}\right)^{\mathrm{T}}d_{k} ∇f(xk)Tdk的σ倍。假设在零点的斜率为下图中绿色曲线所示的-p1,则在点a的斜率应该位于下图中灰色扇形所覆盖的区域内。
我认为可以这样理解这条准则,若在a的斜率不在下图中扇形区域内,可以认为函数值在a处的下降率较大,稍微增大a的值,函数值会有较大的下降,因此,更趋向于取当前位置右侧的值作为a值,因为其位置处函数值更小。

在Wolfe准则中的第二条中,即使σ取为0,亦无法保证满足准则的点接近精确线搜索的结果。因为,其仅仅限制了负斜率较高的情况,即函数值在a点处快速下降的区域,而没有对正斜率较大的区域进行限制,即,函数值在a处快速上升的区域,
若采用下面的强 Wolfe 准则, σ取得越小,满足准则的α越接近精确线搜索的结果
④ 强Wolfe准则
f ( x k + α d k ) ⩽ f ( x k ) + ρ ∇ f ( x k ) T d k α , ∣ ∇ f ( x k + α d k ) T d k ∣ ⩽ − σ ∇ f ( x k ) T d k , \begin{array}{l}f(x_k+\alpha d_k)\leqslant f(x_k)+\rho \nabla f\left(x_{k}\right)^\mathrm{T}d_k\alpha,\\[8pt]| \nabla f(x_k+\alpha d_k)^{\mathrm T}d_k|\leqslant-\sigma \nabla f\left(x_{k}\right)^\mathrm{T}d_k,\end{array} f(xk+αdk)⩽f(xk)+ρ∇f(xk)Tdkα,∣∇f(xk+αdk)Tdk∣⩽−σ∇f(xk)Tdk,

从上图可以看出强 Wolfe 准则对正斜率和负斜率较大的区域都进行了限制,且 σ取得越小,满足强 Wolfe准则的α越接近精确线搜索的结果
其中的σ和ρ满足1>σ >ρ>0,实际应用中控制α不要太小的准则可以不用,因为在线搜索时,只要给定 α k α_k αk一个下界即可.


参考资料:
1、机器人中的数值优化
2、梯度下降
3、数值最优化方法(高立 编著)
相关文章:

机器人中的数值优化(三)—— 无约束最优化方法基础、线搜索准则
本系列文章主要是我在学习《数值优化》过程中的一些笔记和相关思考,主要的学习资料是深蓝学院的课程《机器人中的数值优化》和高立编著的《数值最优化方法》等,本系列文章篇数较多,不定期更新,上半部分介绍无约束优化,…...
vulnhub靶场之bluemoon
1.信息收集 存活主机进行探测,发现主机192.168.239.176存活。 对主机192.168.239.176进行端口扫描,发现21、22、80端口 访问http://192.168.239.176,并查看源码未发现可利用的行为。 进行目录扫描发现可疑路径/hidden_text 浏览器访问h…...
VTK 几何体连通区域分析 vtkPolyDataConnectivityFilter
前言: vtkPolyDataConnectivityFilter 使用过,但网上没有看到完事的教程;这里整理一下; 提取数据集中连通的多边形数据。 该类是一个滤波器,提取cell(区域) - 拥有公共点或者满足某个阈值 该类…...
scss、css样式中使用变量的方法;Vue动态改变css等样式文件中的变量
目录 一、问题 二、原因及解决方法 三、总结 一、问题 1.遇到一些样式 设置的值都是重复的不想重复写,想和js一样定义一个常量,然后直接引用这个常量。 2.想要在js中动态设置样式中的值,在 css、scss等样式表中直接使用。 二、原因及解…...

数据治理在学术上的发展史以及未来展望
数据治理是大数据领域中非常重要的一环,从早期的学术研究到如今的各大企业落地实践,经历了漫长的过程,数据治理的实践落地本身也是一场马拉松。 从百度学术通过精确关键词匹配,搜索中文期刊的“数据治理” 和外文期刊的“data gov…...
【搭建博客】宝塔面板部署Typecho博客,并发布上线访问
目录 前言 1.安装环境 2.下载Typecho 3.创建站点 4.访问Typecho 5.安装cpolar 6.远程访问Typecho 7.固定远程访问地址 8.配置typecho 前言 Typecho是由type和echo两个词合成的,来自于开发团队的头脑风暴。Typecho基于PHP5开发,支持多种数据库&…...
【Spring篇】IOC相关内容
🍓系列专栏:Spring系列专栏 🍉个人主页:个人主页 目录 一、bean基础配置 1.bean基础配置(id与class) 2.bean的name属性 3.bean作用范围scope配置 二、bean实例化 1.构造方法实例化 2.分析Spring的错误信息 3.静态工厂实例化 4.实例工厂 5.FactoryBean 三…...

Python超矩形
文章目录 距离函数矩形分割 Rectangle是 scipy.spatial中封装的类,其构造函数只需输入最小值和最大值的数组即可,并且可通过内置的 volume方法计算广义的体积。 from scipy.spatial import Rectanglerec Rectangle((0,0), (5,5)) print(rec.maxes) …...
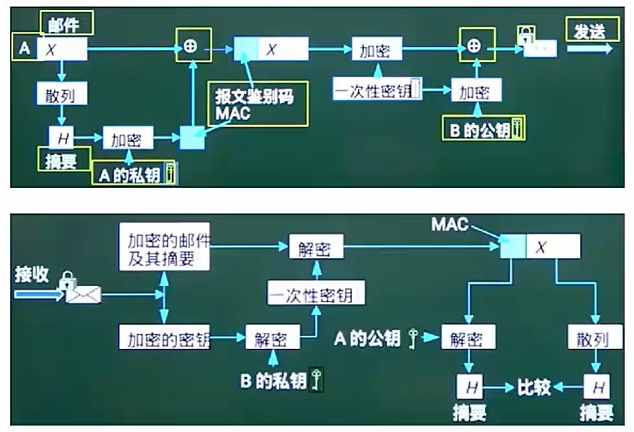
【软考数据库】第五章 计算机网络
目录 5.1 网络功能和分类 5.2 OSI七层模型 5.3 TCP/IP协议 5.4 传输介质 5.5 通信方式和交换方式 5.6 IP地址 5.7 IPv6 5.8 网络规划和设计 5.9 其他考点补充 5.10 网络安全技术 5.11 网络安全协议 前言: 笔记来自《文老师软考数据库》教材精讲ÿ…...

深眸科技|深度学习、3D视觉融入机器视觉系统,实现生产数智化
随着“中国制造2025”战略加速落实,制造业生产线正在加紧向智能化、自动化和数字化转型之路迈进。而人工智能技术的兴起以及边缘算力持续提升的同时,机器视觉及其相关技术也在飞速发展,并不断渗透进工业领域,拓展应用场景的同时&a…...

DateFormat使用时需要注意:多线程下需要特殊处理
前言 工作或学习过程中难免会接触到时间(Date)相关的内容,比如String类型转为Date类型,或者Date类型转为String类型,jdk为我们提供了一套完善的日期格式化工具,DateFormat类,使用者可以使用该接…...
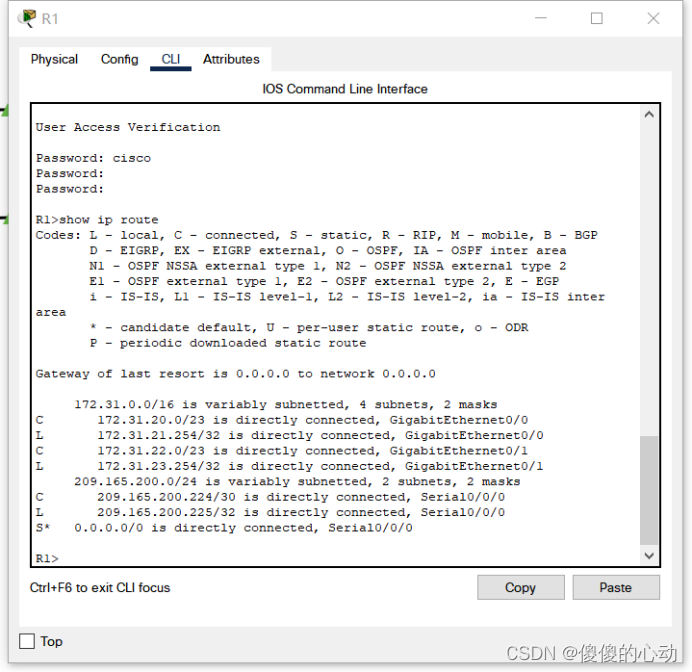
Packet Tracer - 研究直连路由
Packet Tracer - 研究直连路由 目标 第 1 部分:研究 IPv4 直连路由 第 2 部分:研究 IPv6 直连路由 拓扑图 背景信息 本活动中的网络已配置。 您将登录路由器并使用 show 命令发现并回答以下有关直连路由的问题。 注:用户 EXEC 密码是 c…...

大专生程序员找工作的一点小建议 知识分享 经验分享
最近呢有人在私信我 就问我说我呢是一个大专生 大专毕业 学历呢也不是很好 我但是我学的是这个计算机 这样一个专业 然后呢现在找工作找不到 就这样的一个要求 让我们呢给一些建议 当然就是私底下在网上聊吗 就会给 也相信 我的一个建议是什么样的 就是你首先你要去找工作的 首…...

PyCaret:低代码自动化的机器学习工具
PyCaret简介 随着ChatGPT和AI画图的大火,机器学习作为实现人工智能的底层技术被大众越来越多的认知,基于机器学习的产品也越来越多。传统的机器学习实现方法需要较强的编程能力和数据科学基础,这使得想零基础尝试机器学习变得非常困难。 机器…...
【Hello Network】网络编程套接字(三)
作者:小萌新 专栏:网络 作者简介:大二学生 希望能和大家一起进步 本篇博客简介:简单介绍下各种类型的Tcp协议 各种类型Tcp服务器 多进程版的TCP网络程序捕捉SIGCHLD信号让孙子进程执行任务 多线程TCP网络程序线程池版多线程TCP网络…...

3.4 只读存储器
学习目标: 学习只读存储器(ROM)的目标可以包括以下内容: 了解ROM的基本概念、分类以及适用场景。掌握ROM的电路原理、逻辑结构和读取方式。熟悉ROM的编程方式和编程工具。理解ROM与EPROM、EEPROM和闪存的区别和联系。了解ROM在计…...

从后端开发转大数据开发怎么样?
很多做后端的小伙伴,在某一个瞬间,都想转行大数据,那这种想法可行嘛? 转大数据的最初原因很简单,就是好几个同事都转了,他们的收入瞬间提高了好多,于是在同事的内推我也就跟着转了,…...
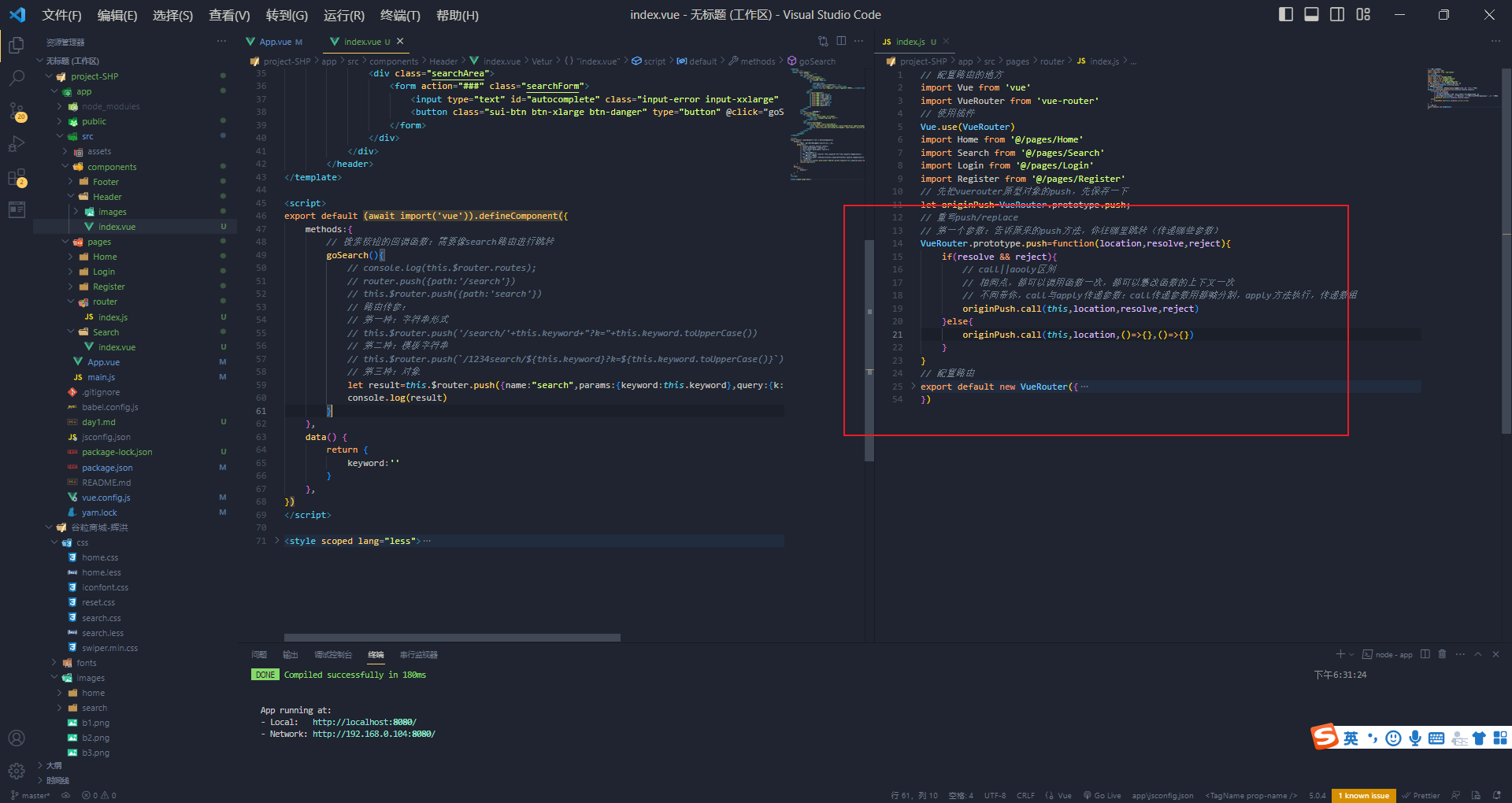
编程式导航路由跳转到当前路由(参数不变),多次执行会抛出NavigatorDuplicated的禁告错误?
重写push与replace方法 编程式导航路由跳转到当前路由(参数不变),多次执行会抛出NavigatorDuplicated的禁告错误? 路由跳转有俩种形式:声明式导航,编程式导航 声明式导航没有这类问题的,因为…...

AppArmor无内核及系统日志的问题及解决
在AppArmor中,正常情况下,一旦违反了规则,是能够在内核及系统日志中看到相关信息的。比如:在Ubuntu下正常产生的日志信息(示例)如下: kernel: [140321.028000] audit(1191433716.584:1578): t…...

本地更改配置ssh密钥和更改github网址
配置 SSH 密钥以进行身份验证,可以遵循以下步骤: 生成SSH密钥 打开 Git Bash 终端 在 Windows 上,可以打开 Git Bash 终端。通常,可以在开始菜单中搜索 Git Bash 并启动它。一旦打开了 Git Bash 终端,将进入一个基于…...

国防科技大学计算机基础课程笔记02信息编码
1.机内码和国标码 国标码就是我们非常熟悉的这个GB2312,但是因为都是16进制,因此这个了16进制的数据既可以翻译成为这个机器码,也可以翻译成为这个国标码,所以这个时候很容易会出现这个歧义的情况; 因此,我们的这个国…...

基于数字孪生的水厂可视化平台建设:架构与实践
分享大纲: 1、数字孪生水厂可视化平台建设背景 2、数字孪生水厂可视化平台建设架构 3、数字孪生水厂可视化平台建设成效 近几年,数字孪生水厂的建设开展的如火如荼。作为提升水厂管理效率、优化资源的调度手段,基于数字孪生的水厂可视化平台的…...

反射获取方法和属性
Java反射获取方法 在Java中,反射(Reflection)是一种强大的机制,允许程序在运行时访问和操作类的内部属性和方法。通过反射,可以动态地创建对象、调用方法、改变属性值,这在很多Java框架中如Spring和Hiberna…...

华为云Flexus+DeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建
华为云FlexusDeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建 前言 如今大模型其性能出色,华为云 ModelArts Studio_MaaS大模型即服务平台华为云内置了大模型,能助力我们轻松驾驭 DeepSeek-V3/R1,本文中将分享如何…...

力扣-35.搜索插入位置
题目描述 给定一个排序数组和一个目标值,在数组中找到目标值,并返回其索引。如果目标值不存在于数组中,返回它将会被按顺序插入的位置。 请必须使用时间复杂度为 O(log n) 的算法。 class Solution {public int searchInsert(int[] nums, …...

return this;返回的是谁
一个审批系统的示例来演示责任链模式的实现。假设公司需要处理不同金额的采购申请,不同级别的经理有不同的审批权限: // 抽象处理者:审批者 abstract class Approver {protected Approver successor; // 下一个处理者// 设置下一个处理者pub…...

Linux 内存管理实战精讲:核心原理与面试常考点全解析
Linux 内存管理实战精讲:核心原理与面试常考点全解析 Linux 内核内存管理是系统设计中最复杂但也最核心的模块之一。它不仅支撑着虚拟内存机制、物理内存分配、进程隔离与资源复用,还直接决定系统运行的性能与稳定性。无论你是嵌入式开发者、内核调试工…...

R 语言科研绘图第 55 期 --- 网络图-聚类
在发表科研论文的过程中,科研绘图是必不可少的,一张好看的图形会是文章很大的加分项。 为了便于使用,本系列文章介绍的所有绘图都已收录到了 sciRplot 项目中,获取方式: R 语言科研绘图模板 --- sciRplothttps://mp.…...

怎么让Comfyui导出的图像不包含工作流信息,
为了数据安全,让Comfyui导出的图像不包含工作流信息,导出的图像就不会拖到comfyui中加载出来工作流。 ComfyUI的目录下node.py 直接移除 pnginfo(推荐) 在 save_images 方法中,删除或注释掉所有与 metadata …...

十九、【用户管理与权限 - 篇一】后端基础:用户列表与角色模型的初步构建
【用户管理与权限 - 篇一】后端基础:用户列表与角色模型的初步构建 前言准备工作第一部分:回顾 Django 内置的 `User` 模型第二部分:设计并创建 `Role` 和 `UserProfile` 模型第三部分:创建 Serializers第四部分:创建 ViewSets第五部分:注册 API 路由第六部分:后端初步测…...
