整数在内存中的存储:原码、反码、补码 大小端字节序

本篇博客会讲解整数在内存中的存储形式,以及整数二进制的3种表示形式:原码、反码、补码,还有大小端的相关知识点。相信读完本篇博客,大家对内存的了解会上一个台阶。
注意:本篇博客讨论的是整数在内存中的存储,像char, short, int, long, long long的有符号和无符号类型存储的都是整数。
认识原码、反码、补码
对于整数,有原码、反码、补码之分,它们都是整数的二进制的表示形式。有符号整数的计算方式如下:
- 正整数的原码、反码、补码相同,都是整数直接转换成二进制的结果。
- 负整数的原码是把该数转换成二进制的结果,反码和补码需要通过原码计算出来。
- 负整数的反码的计算规则:原码的符号位不变,其他位按位取反得到反码。
- 负整数的补码的计算规则:反码+1得到补码。
下面来举2个例子,分别表示正整数和负整数。
正整数以10为例子:10作为十进制数,直接转换成二进制,得到的就是它的原码。又因为10是正整数,故原码、反码、补码相同。所以问题呢就转换成如何把十进制的10转换成二进制。
把十进制的10转换成二进制,得到的是1010。这是怎么来的呢?对于二进制的1010,从右往左数,最右边的0代表0×20,倒数第二位的1代表1×21,倒数第三位的0代表0×22,最左边的1代表1×23,所以二进制的1010就代表十进制的1×23+0×22+1×21+0×20=8+0+2+0=10。
严谨点来说:10的默认类型是int,一个int大小是4个字节,也就是32个bit位,应该填满32位,不够在高位补0,所以10的原码、反码、补码都是:00000000000000000000000000001010。
再举个负数的例子:-10的原码、反码、补码是多少?对于负数,是“有符号数”,最高位表示符号位,用1表示负数,其余的位和10的二进制相同:10000000000000000000000000001010。这就是-10的原码。
-10作为一个负数,反码和补码需要通过原码来计算。反码的计算规则是,原码符号位不变,其他位按位取反,也就是说,最高位的1表示符号位,不变,其余位1变0,0变1。反码就是:11111111111111111111111111110101。
补码的计算规则是:反码+1即是补码,所以-10的补码是:11111111111111111111111111110110。
整数在内存中是以哪种形式存储的呢?事实上,整数在内存中存储的是二进制的补码,这一点是可以验证的,但是同时涉及到大小端的问题。
大小端字节序
大小端字节序,简称大小端,指的是,以字节为单位,内存中的数据是如何存储的。分为2种存储方式,分别是大端字节序和小端字节序,简称大端和小端。
- 大端字节序:把高位字节处的数据存储在低地址处,把低位字节处的数据存储在高地址处。
- 小端字节序:把高位字节处的数据存储在高地址处,把低位字节处的数据存储在低地址处。
这是什么意思呢?我在VS2022环境下验证一下:根据前面所讲,整数在内存中存储的是补码,我们来观察一下-10在内存中是如何存储的。
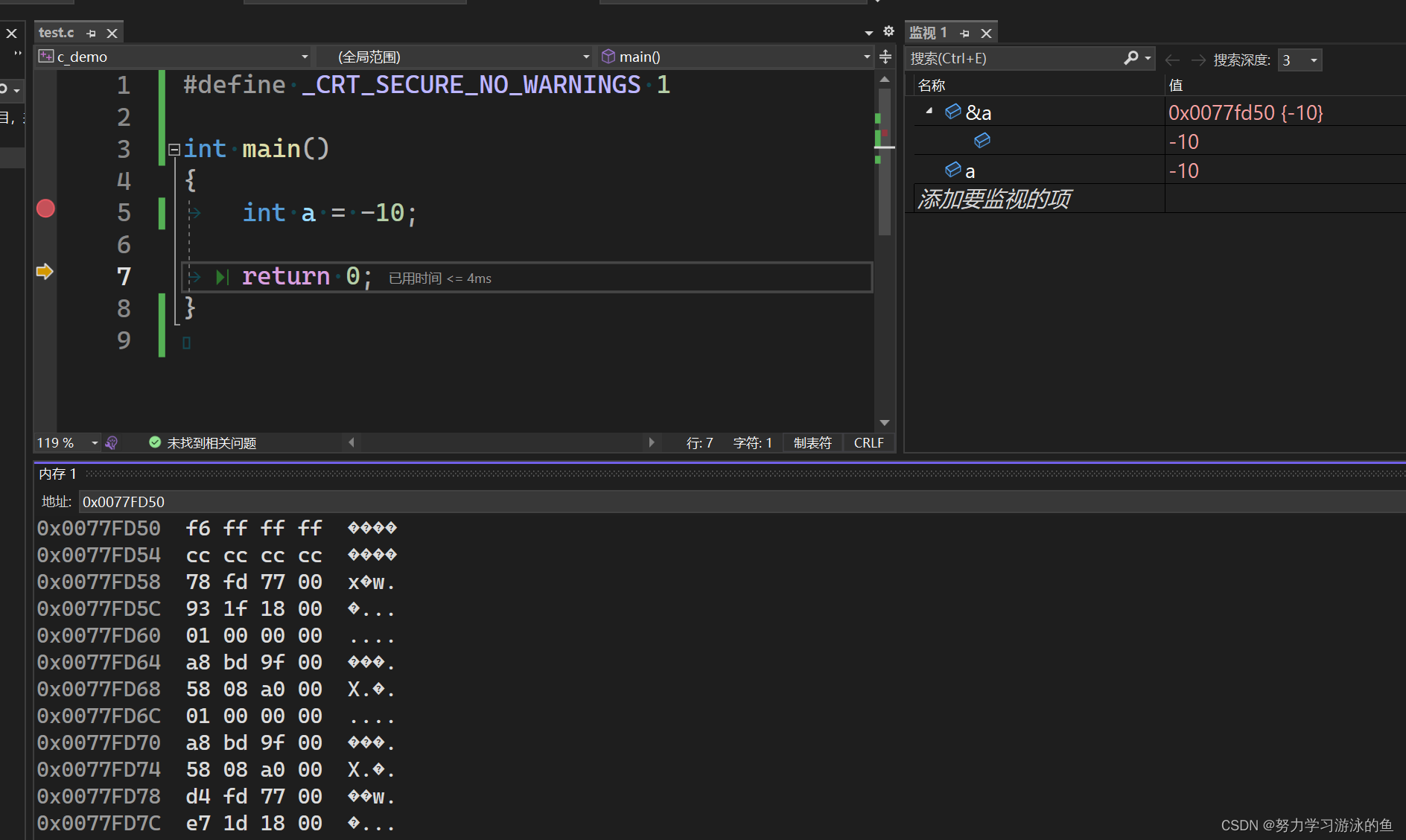
观察到,当左边是低地址,右边是高地址,即地址从左到右是由低到高变化的,此时内存中存储的是0x f6 ff ff ff。这是什么意思呢?
整数在内存中是以二进制的补码的形式存储的。前面计算过了,-10的补码是:11111111111111111111111111110110。下面我们把它转换成十六进制。
先4个为一组分开:1111 1111 1111 1111 1111 1111 1111 0110。
然后分别转换每一组,其中1111是f,0110是6:0x fffffff6。一个十六进制位是4个bit位,2个十六进制位就是一个字节,把这个数以字节为单位分隔开,就是:0x ff ff ff f6。
而内存中存储的却是:0x f6 ff ff ff,这是为什么呢?在VS环境下观察内存,从左到右,地址是由低到高变化的,也就是说,本来-10补码中的高位的ff存储在了高地址处,而-10补码中的低位的f6存放在低地址处,这就是“小端字节序”的存储方式,看起来像是数据“倒着放”。
整数在内存中的存储
整数在内存中的存储,是由以下2点决定的:
- 整数在内存中存储的是补码的二进制。
- 根据机器是“大端字节序”还是“小端字节序”来决定是“正着放”还是“倒着放”。
以上是数据“如何存”,那如何把一个数据“往外拿”呢?把存的过程倒过来就行了。
- 根据大小端字节序,把数据“正着”或者“倒着”拿出来。
- 把拿出来的补码转换成原码。
那如何把补码转换成原码呢?原码怎么转换成补码,把这个过程倒过来就行了,以下是如何把补码解析成有符号数的过程。
- 若符号位是0,则是正数,此时原码、反码都和补码相同。若符号位是1,则是负数,需要计算反码和原码。
- 补码-1得到反码。
- 反码的符号位不变,其他位按位取反得到原码。
注意:如果要解析成无符号数,最高位就不是符号位了,而是数据的一部分,此时一律看做正整数来处理。
举个例子,前面我们观察到小端机器下-10在内存中存储的是:0x f6 ff ff ff,由于小端是“倒着存”的,所以先正过来:0x ff ff ff f6,再转换成二进制:1111 1111 1111 1111 1111 1111 1111 0110,即11111111111111111111111111110110,这就是补码,由于符号位(最高位)是1,是一个负数,需要根据补码计算反码和原码。先把补码-1,得到反码:11111111111111111111111111110101,把反码符号位不变,其他位按位取反得到原码:10000000000000000000000000001010,再转换成十进制,就得到了-10。
为什么要存补码?
整数在内存中存储的是补码的二进制,这主要有2个优点。
先说第一个优点:使用补码来存储,统一了符号位和数值位。换句话说,符号位和数值为可以统一计算。在CPU中,只有加法器,所有的计算都要转换成加法。比如,计算1-1,先要转换成计算1+(-1),然后写出1和-1的补码:
1作为正数,原码、反码、补码相同,都是:00000000000000000000000000000001
-1作为负数,原码是:10000000000000000000000000000001,原码符号位不变,其他位按位取反后得到反码:11111111111111111111111111111110,反码+1得到补码:11111111111111111111111111111111。
接下来计算1+(-1),也就是这样计算:
00000000000000000000000000000001
+ 11111111111111111111111111111111100000000000000000000000000000000
由于整数只能存储32个bit为,最高位的1就丢了,只剩下00000000000000000000000000000000,得到的结果就是0。
根据以上的计算,有没有发现,我们根本没有管哪里是符号位,哪里是数值位,就是简单粗暴的把补码写出来,加起来,完事。CPU把内存中存储的补码拿出来,进行加法运算时,根本不用考虑哪里是符号位,那里是数值位,这就做到了把符号位和数值位统一处理。
在说第二个优点之前,还需要了解一个知识点:把补码转换成原码的另一种方式:先把补码的符号位不变,其他位按位取反,再+1,也能得到原码。比如:已知-10的补码:11111111111111111111111111110110,把补码的符号位不变,其他位按位取反得到:10000000000000000000000000001001,再+1得到:10000000000000000000000000001010,这样也得到了-10的原码。
有没有发现,如果用这种方式把补码转原码,那么就和原码转补码的方式相同了,都是“取反再+1”!所以,用补码来存储时,把补码转原码,以及原码转补码可以使用同一套硬件电路,降低了电路的复杂性。
总结
- 整数的2进制有3种表示形式,分别是原码、反码、补码。
- 正整数的原码、反码、补码相同,负整数的原码、反码、补码需要计算。把整数直接转换成2进制,就是原码。负整数的原码的符号位不变、其他位按位取反得到反码。负整数的反码+1得到补码。
- 从补码转原码,需要先看符号位,确定是正数还是负数,如果是正数,则原码、反码、补码相同。如果是负数,则可以先-1得到反码,再符号位不变,其他位按位取反得到原码;也可以先符号位不变,其他位按位取反,再+1得到原码。注意:无符号数一律按照正数来处理。
- 大小端字节序分为大端字节序和小端字节序。大端字节序指的是,把高位字节处的数据存储在低地址处,把低位字节处的数据存储在高地址处。小端字节序指的是,把高位字节处的数据存储在高地址处,把低位字节处的数据存储在低地址处。
- 内存中使用补码来存储整数有2个好处:统一处理符号位和数值位,以及使用同一套硬件电路来把原码和反码相互转换,降低电路复杂性。
感谢大家的阅读!
相关文章:

整数在内存中的存储:原码、反码、补码 大小端字节序
本篇博客会讲解整数在内存中的存储形式,以及整数二进制的3种表示形式:原码、反码、补码,还有大小端的相关知识点。相信读完本篇博客,大家对内存的了解会上一个台阶。 注意:本篇博客讨论的是整数在内存中的存储&#x…...
【方法】 如何批量将RAR或其他压缩格式转换成ZIP?
压缩文件的格式有很多种,比如RAR、ZIP、7-Zip、CAB、ARJ、ACE、TAR、BZ2等等。因为需求不同,或者不同平台对上传的压缩包格式要求不同,我们往往需要把压缩文件进行格式转换,那压缩文件不同格式之间如何进行转换呢? 如…...

《道德经》
《道德经》是春秋时期老子(李耳)的哲学作品,又称《道德真经》、《老子》、《五千言》、《老子五千文》,是中国古代先秦诸子分家前的一部著作,是道家哲学思想的重要来源。 道德经分上下两篇,原文上篇《德经…...

ABI Research产业研究:ZiFiSense如何革新物流货物及运输包装追踪
“文章源自前沿科技研究机构ABI Research产业研究,重点介绍了ZETA LPWA协议开发公司纵行科技在业务发展、M-FSK调制技术以及ZETag云标签系列产品在物流货物追踪与包装管理等方面的应用分析,还分享了纵行科技ZETA技术在商业市场和生态系统方面的发展情况。…...
家乡特色推荐系统~java~mysql
摘 要 在Internet高速发展的今天,我们生活的各个领域都涉及到计算机的应用,其中包括家乡特色推荐的网络应用,在外国家乡特色推荐系统已经是很普遍的方式,不过国内的管理网站可能还处于起步阶段。家乡特色推荐系统采用java技术&…...
二维码在设备点维一体化管理中的应用
随着科技发展,设备点维一体化管理体系应运而生,该管理体系的出现让设备维护保养变得更加高效精细化。 设备点维一体化管理体系以设备点检和维护保养为基础,通过日常、专业及精密点检,对点检测得的数据和设备给油脂保养情况进行统…...

基于simulink使用混合波束成形对射频毫米波发射器进行建模
一、前言 本例说明了一种使用66元件混合波束成形天线对32 GHz QPSK射频发射和接收系统进行系统级建模和仿真的方法。该系统包括射频缺陷、发射阵列辐射效应、窄带接收阵列和基带接收器,可校正系统损伤和消息解码。天线波束形成方向使用方位角和仰角定义,…...

面试官:v-model原理?
什么是v-model v-model是Vue框架中的一个指令,用来实现双向数据绑定。它能够在表单元素(如输入框、复选框等)和Vue实例中的数据属性之间建立起一条双向数据通道,使得当表单元素的值发生改变时,对应的数据属性也会相应…...

兰林:科技赋能健康产业 助力乡村振兴建设
万民健康创始人 万民智养中医创始人 万民星农CEO兰林 党建引领谋发展 , 旗帜下乡促振兴 。 乡村振兴,健康先行。自党的十八大以来,国家卫健委贯彻落实“以基层为重点”的党的卫生与健康工作方针,推动医疗卫生工作重心下移、资源下…...

小红书流量密码是什么,怎么掌握并运用
现在是个流量的社会,因为流量其实代表的就是收益,那面对一个流量时代,小红书现在而言毫无疑问是蓝海,品牌想要做好,自然要掌握平台流量密码。今天来和大家一起分享一下小红书流量密码有什么,流量密码可以用…...

FL Studio 2023中文高级版水果编曲软件下载
FL Studio 2023中文版是一款非常经典的音乐制作软件,这款软件除了可以为用户提供全面的音乐制作功能之外,还有丰富的主题和皮肤供用户选择,让用户不但做出的音乐具有自己的风格,连制作的音乐的过程也个性十足,非常适合…...

浅析如何写出高质量代码
你是否曾经为自己写的代码而感到懊恼?你是否想过如何才能写出高质量代码?那就不要错过这个话题!在这里,我们可以讨论什么是高质量代码,如何写出高质量代码等问题。无论你是初学者还是资深开发人员,都可以在…...

手把手教你 ,带你彻底掌握八大排序算法【数据结构】
文章目录 插入排序直接插入排序希尔排序 选择排序选择排序堆排序升序 交换排序冒泡排序快速排序递归hoare版本挖坑法前后指针版本 非递归Hoare挖坑法前后指针 快排的优化三数取中法选key递归到小的子区间时,可以考虑使用插入排序 归并排序递归实现非递归实现 排序算…...
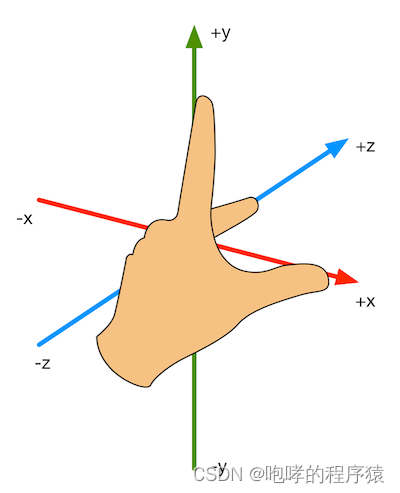
第十一章 Transform组件(上)
本章节我们介绍Transform类,它是一个组件,每一个游戏对象有拥有该组件。因此,它值得我们重点介绍一下。Transform代表了游戏对象的世界变换,也就是移动,选择和缩放。 首先,我们先介绍它的属性(…...
aac音频怎么转mp3,这几个方法很简便
对于aac来说,其是一种高级音频编码,也是专门为声音数据设计的文件压缩格式。通常来说,aac与mp3有一些不同。aac使用了全新的算法进行编码的,其整体的效率较mp3更高一些。同时,aac格式的音质较好一些。但是,…...
分屏视图上线,详情数据秒切换
分屏视图 路径 表单 >> 表单设计 功能简介 新增「分屏视图」。分屏视图是一种对数据阅读提供沉浸式体验的视图组织形式,用户可通过分屏视图更快速的查看数据详情。 使用场景: 对于数据类型是「订单」数据的表单,管理人员往往会对…...
怎么释放C盘空间?清理C盘空间的4大方法分享!
案例:怎么释放c盘空间 【朋友们,最近我的c盘空间内存严重不足了,想释放一下c盘的空间,大家有什么好的方法吗?】 在使用电脑的过程中,经常会遇到C盘空间不足的问题,这时候就需要释放C盘的空间。…...
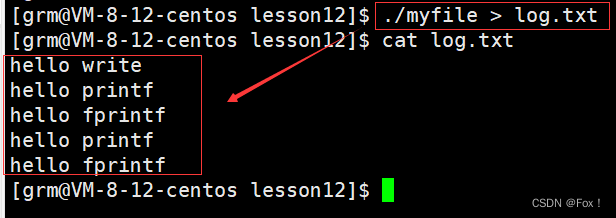
【文件描述符|重定向|缓冲区】
1 C语言文件操作的回顾 这块博主在讲解C语言时就已经做了很详细的讲解,这里就不详细讲了,直接给出代码。 写操作: #include<stdio.h> #include<stdlib.h> #include<errno.h> #define LOG "log.txt" …...
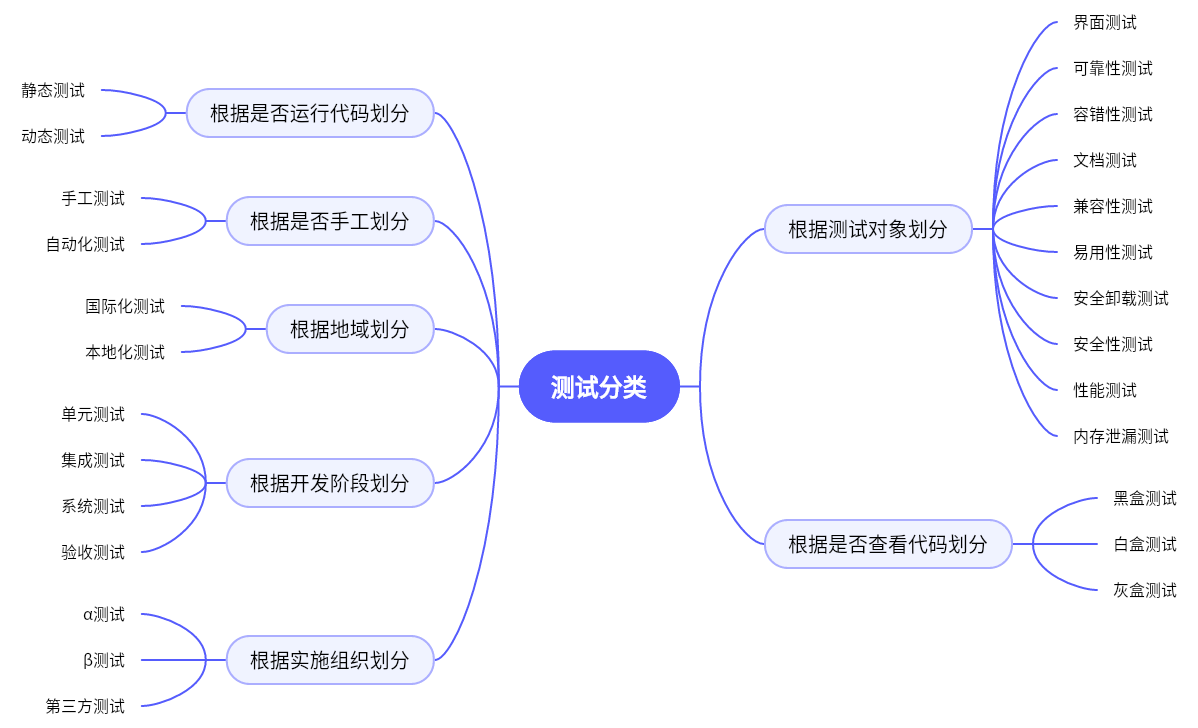
软件测试—进阶篇
软件测试—进阶篇 🔎根据测试对象划分界面测试可靠性测试容错性测试文档测试兼容性测试易用性测试安装卸载测试安全性测试性能测试内存泄漏测试 🔎根据是否查看代码划分黑盒测试白盒测试灰盒测试 🔎根据开发阶段划分单元测试集成测试系统测试…...

设计模式:创建型设计模式、结构型设计模式
目录 前言如何学习设计模式?设计模式基础设计原则 一. 创建型设计模式1. 模板方法2. 观察者模式3. 策略模式 二. 结构型设计模式1. 单例模式2. 工厂模式3. 抽象工厂4. 责任链5. 装饰器6. 组合模式 前言 如何学习设计模式? 明确目的 在现有的设计模式上…...
)
uniapp 对接腾讯云IM群组成员管理(增删改查)
UniApp 实战:腾讯云IM群组成员管理(增删改查) 一、前言 在社交类App开发中,群组成员管理是核心功能之一。本文将基于UniApp框架,结合腾讯云IM SDK,详细讲解如何实现群组成员的增删改查全流程。 权限校验…...

19c补丁后oracle属主变化,导致不能识别磁盘组
补丁后服务器重启,数据库再次无法启动 ORA01017: invalid username/password; logon denied Oracle 19c 在打上 19.23 或以上补丁版本后,存在与用户组权限相关的问题。具体表现为,Oracle 实例的运行用户(oracle)和集…...

深入理解JavaScript设计模式之单例模式
目录 什么是单例模式为什么需要单例模式常见应用场景包括 单例模式实现透明单例模式实现不透明单例模式用代理实现单例模式javaScript中的单例模式使用命名空间使用闭包封装私有变量 惰性单例通用的惰性单例 结语 什么是单例模式 单例模式(Singleton Pattern&#…...

Java-41 深入浅出 Spring - 声明式事务的支持 事务配置 XML模式 XML+注解模式
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

Robots.txt 文件
什么是robots.txt? robots.txt 是一个位于网站根目录下的文本文件(如:https://example.com/robots.txt),它用于指导网络爬虫(如搜索引擎的蜘蛛程序)如何抓取该网站的内容。这个文件遵循 Robots…...
)
Java入门学习详细版(一)
大家好,Java 学习是一个系统学习的过程,核心原则就是“理论 实践 坚持”,并且需循序渐进,不可过于着急,本篇文章推出的这份详细入门学习资料将带大家从零基础开始,逐步掌握 Java 的核心概念和编程技能。 …...

学习STC51单片机32(芯片为STC89C52RCRC)OLED显示屏2
每日一言 今天的每一份坚持,都是在为未来积攒底气。 案例:OLED显示一个A 这边观察到一个点,怎么雪花了就是都是乱七八糟的占满了屏幕。。 解释 : 如果代码里信号切换太快(比如 SDA 刚变,SCL 立刻变&#…...

技术栈RabbitMq的介绍和使用
目录 1. 什么是消息队列?2. 消息队列的优点3. RabbitMQ 消息队列概述4. RabbitMQ 安装5. Exchange 四种类型5.1 direct 精准匹配5.2 fanout 广播5.3 topic 正则匹配 6. RabbitMQ 队列模式6.1 简单队列模式6.2 工作队列模式6.3 发布/订阅模式6.4 路由模式6.5 主题模式…...

高考志愿填报管理系统---开发介绍
高考志愿填报管理系统是一款专为教育机构、学校和教师设计的学生信息管理和志愿填报辅助平台。系统基于Django框架开发,采用现代化的Web技术,为教育工作者提供高效、安全、便捷的学生管理解决方案。 ## 📋 系统概述 ### 🎯 系统定…...

论文阅读:Matting by Generation
今天介绍一篇关于 matting 抠图的文章,抠图也算是计算机视觉里面非常经典的一个任务了。从早期的经典算法到如今的深度学习算法,已经有很多的工作和这个任务相关。这两年 diffusion 模型很火,大家又开始用 diffusion 模型做各种 CV 任务了&am…...
