Lecture3 梯度下降(Gradient Descent)
目录
1 问题背景
2 批量梯度下降 (Batch Gradient Descent)
3 鞍点(Saddle Point)
3 随机梯度下降 (Stochastic Gradient Descent)
4 小批量梯度下降 (Mini-batch Gradient Descent)
1 问题背景
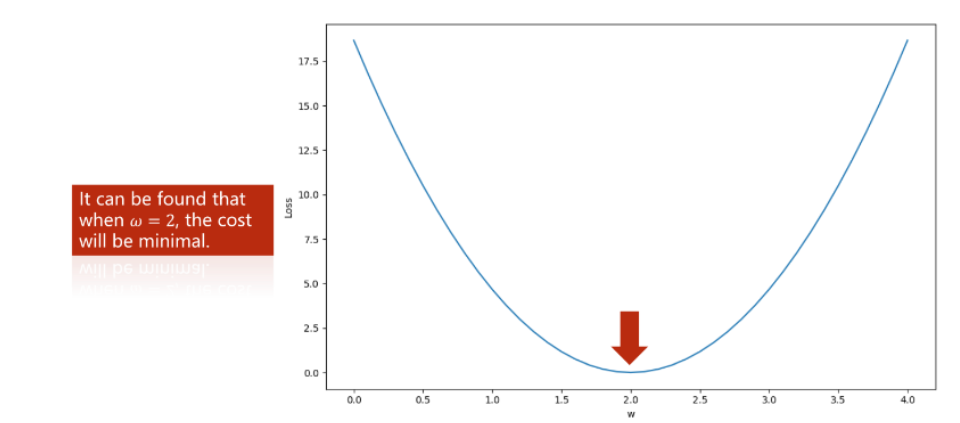
在Lecture2中,介绍了使用穷举法来确定最优值,然而当遇到
范围较大,或者数量过多等情况时,穷举法的时间复杂度过大。因此,我们需要优化该算法。
2 批量梯度下降 (Batch Gradient Descent)
在这次课中,介绍了一种寻找最优值的算法——批量梯度下降 (Batch Gradient Descent, BGD)
简单介绍下该算法。首先对于下图:
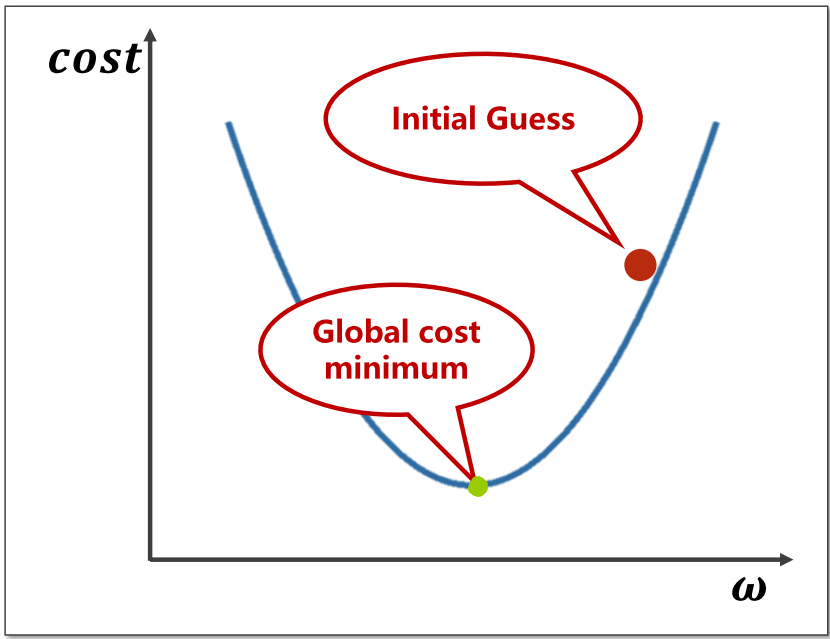
假设我们目前的起始位于上图红色点,为了找到最优
点(位于绿点),那么我们需要向左边移动,这样才能到达最优
点。
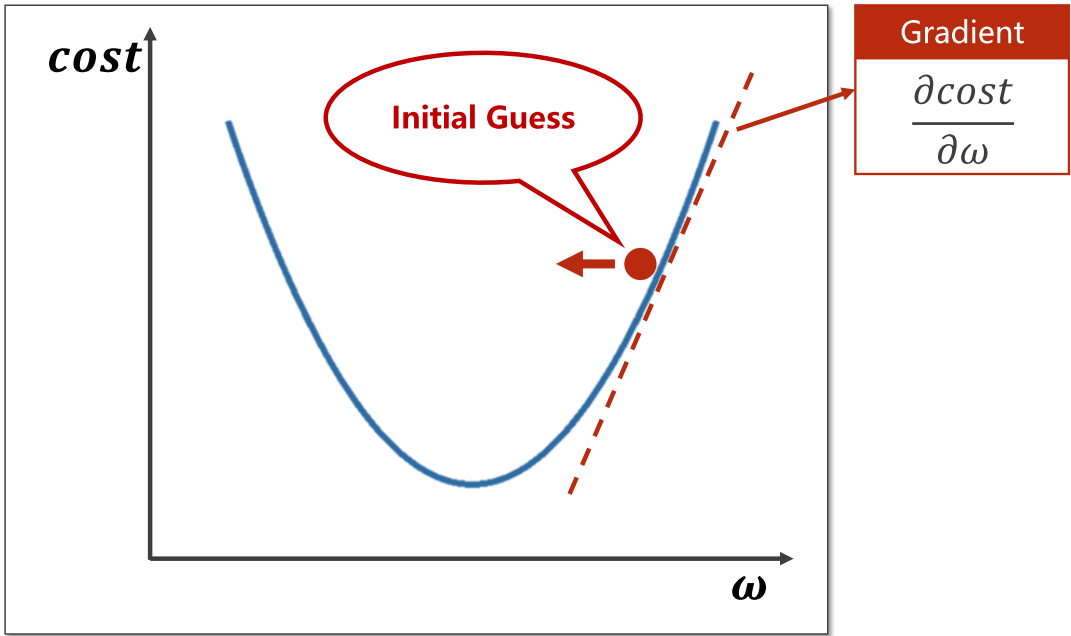
如何让权值点向左还是向右移动呢?此时我们需要计算当前点的梯度(Gradient),也就是用成本函数对权重进行求导,如果梯度<0,则向函数值递减方向移动;梯度>0,则向函数值递增方向移动。
因为要移动起来,所以我们每移动一步,就要更新一下值。更新函数如下图Update处:
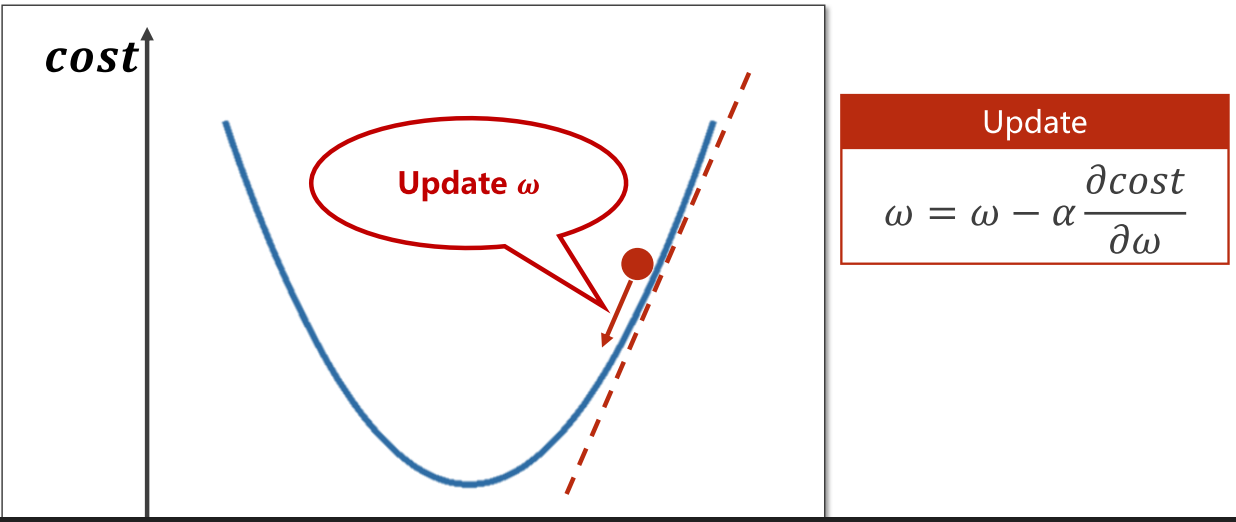
在这个更新函数中, α代表学习率(Learning Rate),学习率是机器学习中常用的一个超参数,它定义了每次更新参数时步长的大小,即每次更新参数时参数值变化的幅度。如果学习率设置得过大,所求结果可能会在最优解的附近来回震荡,而无法找到全局最优解。如果学习率设置得过小,那么模型的训练将会非常缓慢,甚至找不到最优解。
这个式子中,梯度前面用了减号,是为了朝函数值递减方向,也就是往最优所在的点移动,所以在梯度前面加负号。 就这样持续一步步地更新
,直到找到最优
。
下面我们来具体讲讲如何去计算更新函数中的 :

计算过程中,需要用到上节课总结的两个公式:
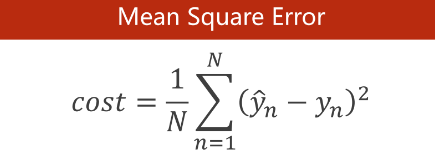

接着把上述两个公式代入原式:

蓝色处,因为cost=MSE,所以直接代入上一节课的MSE公式,然后对求导。
绿色处,由有理运算法则,和的导数等于导数的和,所以这里可以把移入求和式子中,对里面先进行求导后,再求和相加。
黄色处,根据复合导数的链式求导法进行求导。
代码实现
from matplotlib import pyplot as pltx_data = [1.0, 2.0, 3.0]
y_data = [2.0, 4.0, 6.0]
w = 1.0 # 初始权重,由这个权重开始迭代'''线性模型,算出预测值y_hat'''
def forward(x):return x * w'''均方误差MSE'''
def cost(xs, ys):cost = 0for x, y in zip(xs, ys):y_pred = forward(x) # 算出y_hatcost += (y_pred - y) ** 2 # (y_hat - y)²return cost / len(xs) # 除以样本总数求均值'''梯度下降公式'''
def gradient(xs, ys):grad = 0for x, y in zip(xs, ys):grad += 2 * x * (x * w - y)return grad / len(xs)print('Predict (before training)', 4, forward(4)) # 训练前,模型对输入的4的最终预测结果cost_list = [] # 保存每轮迭代后的cost值
epoch_list = [] # 保存每轮的迭代后的epoch值
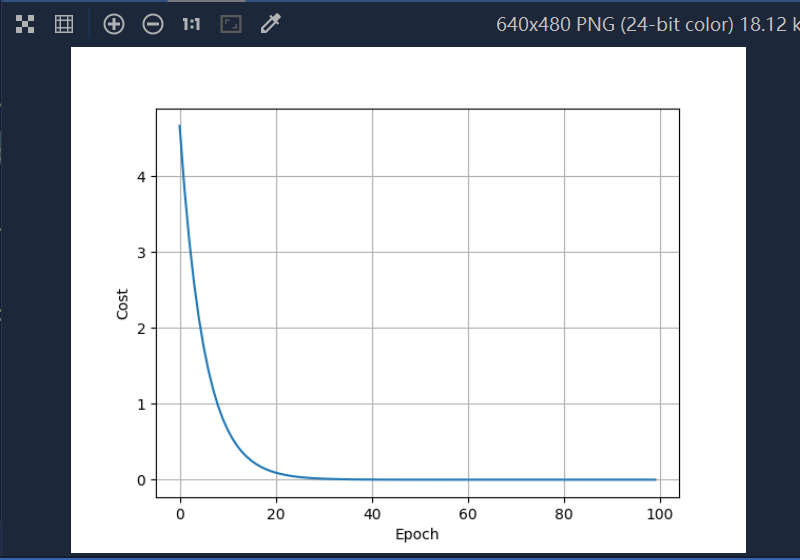
for epoch in range(100): # 进行100轮训练cost_val = cost(x_data, y_data)grad_val = gradient(x_data, y_data)w -= 0.01 * grad_val # 使用梯度下降法更新权重,0.01表示学习率print('Epoch:', epoch, 'w=%.2f' % w, 'loss=%.2f' % cost_val)cost_list.append(cost_val)epoch_list.append(epoch)
print('Predict (after training)', 4, forward(4)) # 训练后,模型对输入的4的最终预测结果'''绘图'''
plt.plot(epoch_list, cost_list)
plt.ylabel('Cost')
plt.xlabel('Epoch')
plt.grid()
plt.show()
将MSE公式和Linear Model公式代入整合,的最终更新函数:

补充
训练后的结果一般来说,cost会趋于收敛情况

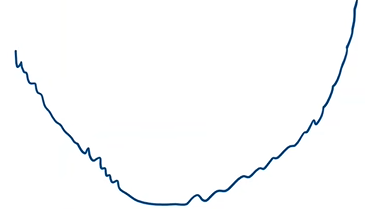
如果发生如下情况,说明训练失败,原因有很多,其中之一可能是学习率取得太大:
这就是批量梯度下降算法,本质上是一个贪心算法(Greedy Algorithm)。不过该算法有局限性,比如当前的预测值正好位于下图绿线处,因为再往右移动会梯度会发生变化,使得程序直接终止,于是误将红的点作为最优
值,而忽略了处于蓝色点的最优
值:
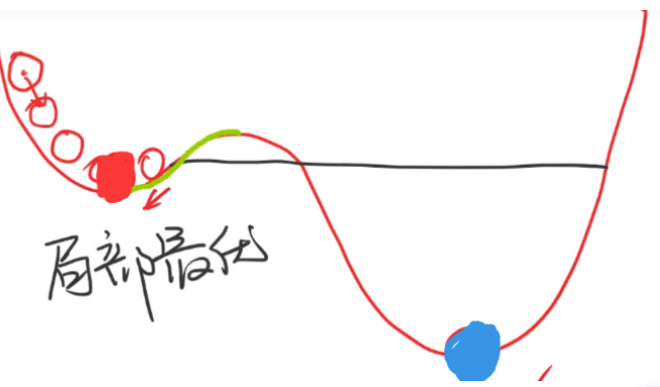
我们把上图中的红点称为局部最优点(Local Optimum),蓝色点称为全局最优点(Global Optimum)。因此对于该梯度下降算法,很可能会找到局部最优点,而忽略了全局最优点。不过这种现象不必担心,因为在实际训练中,往往很难陷入局部最优点。
3 鞍点(Saddle Point)
在实际训练中,往往很难陷入局部最优点,而最需要解决的问题是鞍点(Saddle Point),鞍点是机器学习和数学中的一个概念,它指的是一个特殊的局部极小值,在某些方向上是极小值,但在其他方向上是极大值。在一元函数中,梯度=0的点就是鞍点。比如下图中,红色小球所处的位置就在鞍点,此时梯度为零,会导致更新函数无法更新(因为梯度=0,=
-α*0相当于没有发生更新):

从多维角度来分析,比如下图红球处于马鞍面(Saddle Surface),从一个切面看可以处于最小值,从另一个切面看又处于最大值:
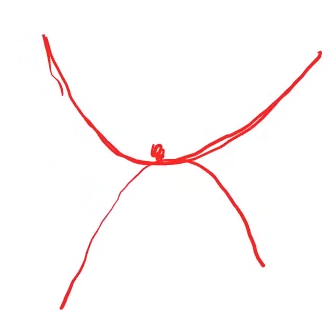
在优化问题中,鞍点是一种特殊的局部最优解,是一个难以优化的点,因为优化算法可能很难从鞍点附近找到全局最优解。这是因为,如果优化算法在鞍点附近搜索,它可能会被误导到其他附近的局部最优解,而不是真正的全局最优解。所以在深度学习中,需要克服的最大问题就是鞍点而非局部最优问题。
3 随机梯度下降 (Stochastic Gradient Descent)
随机梯度下降 (Stochastic Gradient Descent, SGD)在深度学习中很常用,和BGD算法的区别是,BGD使用所有的样本的均值的平均损失来作为的更新依据,而SGD是从所有样本中随机选择单个样本的损失值来对
进行更新。
随机梯度下降的优点是,每次仅使用一个数据点的梯度,因此在每次迭代时都有可能沿着非0梯度的方向更新参数,这样就避免陷入到鞍点导致无法更新参数。

代码实现
import randomx_data = [1.0, 2.0, 3.0]
y_data = [2.0, 4.0, 6.0]
w = 1.0def forward(x):return x * wdef loss(x, y):y_pred = forward(x)return (y_pred - y) ** 2def gradient(x, y):return 2 * x * (x * w - y)print('Predict (before training)', 4, forward(4))
for epoch in range(100):t = random.randrange(0, 3) # 随机得到一个样本x = x_data[t]y = y_data[t]grad = gradient(x, y)w = w - 0.01 * gradprint("\tgrad: ", x, y, '%.2f' % grad)l = loss(x, y)print("progress:", epoch, "w=%.2f" % w, "loss=%.2f" % l)
print('Predict (after training)', 4, forward(4))
部分输出结果
Predict (before training) 4 4.0
grad: 3.0 6.0 -18.00
progress: 0 w=1.18 loss=6.05
grad: 2.0 4.0 -6.56
progress: 1 w=1.25 loss=2.28
grad: 3.0 6.0 -13.58
progress: 2 w=1.38 loss=3.44
grad: 1.0 2.0 -1.24
progress: 3 w=1.39 loss=0.37
grad: 2.0 4.0 -4.85
progress: 4 w=1.44 loss=1.24···
grad: 1.0 2.0 -0.00
progress: 97 w=2.00 loss=0.00
grad: 1.0 2.0 -0.00
progress: 98 w=2.00 loss=0.00
grad: 2.0 4.0 -0.00
progress: 99 w=2.00 loss=0.00
Predict (after training) 4 7.999910864525451
4 小批量梯度下降 (Mini-batch Gradient Descent)
SGD算法虽然可以在一定程度上避免陷入局部最优以及鞍点问题,但是运算所需时间复杂度过高,每次仅使用一个数据点的梯度,因此它的收敛速度通常比较慢。
因此有一个折中的办法,就是使用小批量梯度下降 (Mini-batch Gradient Descent) 算法。简单来说,小批量梯度下降是一种介于批量梯度下降和随机梯度下降之间的优化算法。结合了这两种方法,通过使用小的随机选择的训练数据子集(称为mini-batch)计算损失函数关于参数的梯度的平均值来更新模型参数。
总之,小批量梯度下降算法实现了BGD的高计算效率和SGD的良好收敛性之间的平衡。
相关文章:

Lecture3 梯度下降(Gradient Descent)
目录 1 问题背景 2 批量梯度下降 (Batch Gradient Descent) 3 鞍点(Saddle Point) 3 随机梯度下降 (Stochastic Gradient Descent) 4 小批量梯度下降 (Mini-batch Gradient Descent) 1 问题背景 图1 上节课讲述的穷举法求最优权重值在Lecture2中,介绍了使用穷举…...

深入了解DSP
一、时钟和电源 问:DSP的电源设计和时钟设计应该特别注意哪些方面?外接晶振选用有源的好还是无源的好? 答:时钟一般使用晶体,电源可用TI的配套电源。外接晶振用无源的好。 问:TMS320LF2407的A/D转换精度保证…...
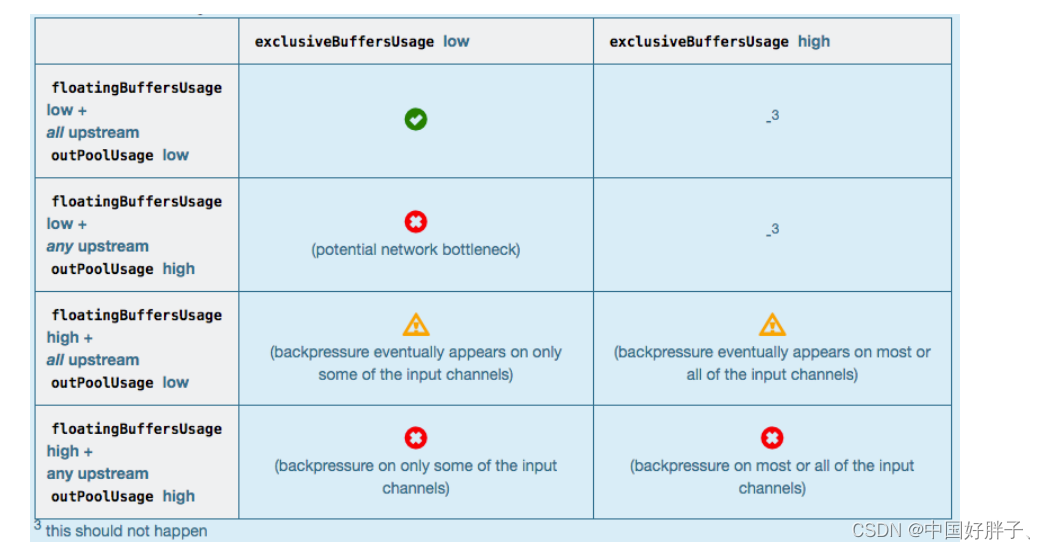
Flink反压如何排查
Flink反压利用了网络传输和动态限流。Flink的任务的组成由流和算子组成,那么流中的数据在算子之间转换的时候,会放入分布式的阻塞队列中。当消费者的阻塞队列满的时候,则会降低生产者的处理速度。 如上图所示,当Task C 的数据处…...
windows无法访问指定设备路径或文件怎么办?2个解决方案
有时候Win10电脑打不开程序或文件,windows无法访问指定设备路径或文件该怎么办?原因是什么呢?一般导致这种情况的出现,大多是因为我们的电脑缺乏相应的查看权限,我们只需要通过赋予权限就可以解决这个难题了。 操作环境…...

冷知识|鹤顶红还能用来修长城?
大家好,我是建模助手。 在上篇浅浅地蹭了波热点之后,我灵机一动,倒不如也搞一搞建筑方面的冷知识?冷热搭配,事半功倍... 问问大家,如果谈起古建筑,关键词都有什么?是庄严、震撼、壮…...
【GD32F427开发板试用】在IAR环境中移植RTX5
本篇文章来自极术社区与兆易创新组织的GD32F427开发板评测活动,更多开发板试用活动请关注极术社区网站。作者:吴金刚 0.前言 首先感谢极术社区和兆易创新给了这次试用GD32F427开发板的机会。 板子做的虽然简约,但是自带了GD-link所以一根USB…...
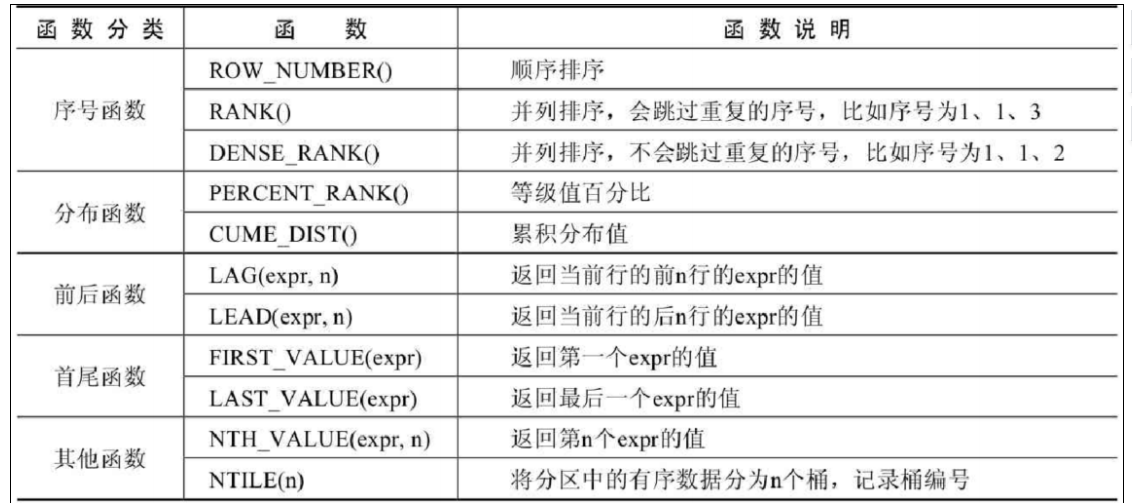
MySQl学习(从入门到精通15)
MySQl学习(从入门到精通15)第 18 章_MySQL 8 其它新特性1. MySQL 8 新特性概述1. 1 MySQL 8. 0 新增特性1. 2 MySQL 8. 0 移除的旧特性2. 新特性 1 :窗口函数2. 1 使用窗口函数前后对比2. 2 窗口函数分类2. 3 语法结构2. 4 分类讲解1. 序号函…...

前端构建工具 Vite
文章目录参考环境构建工具构建工具的主要功能目前主流的前端构建工具Vite为什么使用 Vite冷启动WebpackVite热更新优化热更新优化预构建依赖Webpack VS ViteVite 的缺点首屏性能懒加载与 Vite 相关的基本操作获取create-vite创建项目Project nameSelect a frameworkSelect a va…...

若依框架---PageHelper分页(十)
在前几天的文章中,我们介绍了PageHelper的分页方法,研读代码定位到了ExecutorUtil.pageQuery(...)方法,并阅读到了其中的部分代码。 今天我们将看到重要的SQL修改代码。 getPageSql 我们接着看代码: if (!dialect.beforePage(…...

苹果手机专用蓝牙耳机有哪些?与iphone兼容性好的蓝牙耳机
蓝牙耳机摆脱了线缆的束缚,在地以各种方式轻松通话。自从蓝牙耳机问世以来,一直是行动商务族提升效率的好工具,苹果产品一直都是受欢迎的数码产品,下面推荐几款与iphone兼容性好的蓝牙耳机。 第一款:南卡小音舱蓝牙耳…...

CS-TPGS;壳聚糖修饰维生素E;Chitosan-g-TPGS
Chitosan-g-TPGS,CS-TPGS壳聚糖修饰维生素E聚乙二醇1000琥珀酸酯外观呈现白色固体或者粘稠液体。长期保存需要在-20℃,避光,干燥条件下存放,注意取用一定要干燥,避免频繁溶冻。 维生素E聚乙二醇琥珀酸酯(简称TPGS)是维生素E的水溶性衍生物,由维生素E琥珀酸酯的羧基与…...

easyx的基本使用(万字解析)
easyx的基本使用一.基本框架1.创建文件2.创建窗体-initgraph,closegraph,getchar二.简单的绘制1.圆形-circle2.坐标系统-setorigin,setaspectratio三.简单图形1.绘制点-putpixel2.简单的直线-line3.矩形-rectangle4.椭圆-ellipse5.圆角矩形-roundrect6.扇形-pie7.圆弧-arc四.多…...
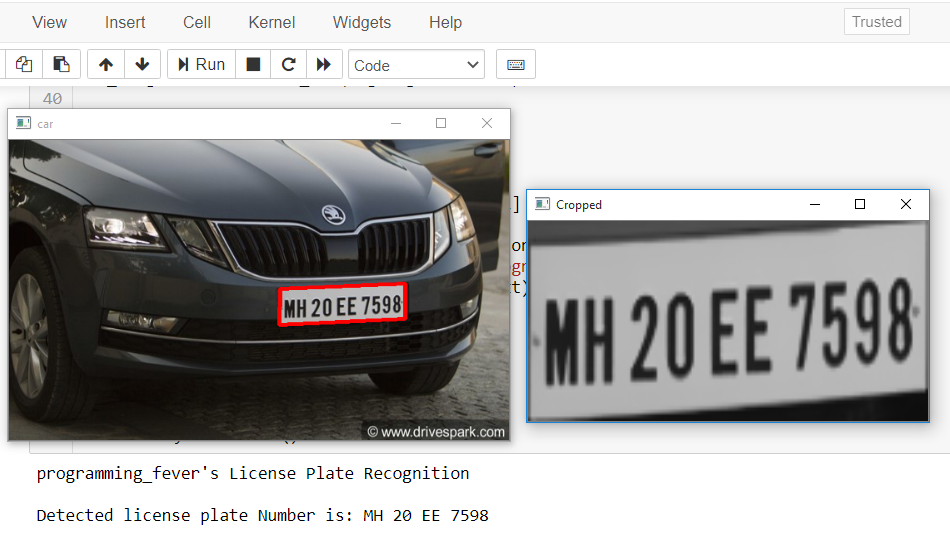
基于OpenCV 的车牌识别
基于OpenCV 的车牌识别 车牌识别是一种图像处理技术,用于识别不同车辆。这项技术被广泛用于各种安全检测中。现在让我一起基于 OpenCV 编写 Python 代码来完成这一任务。 车牌识别的相关步骤 1. 车牌检测:第一步是从汽车上检测车牌所在位置。我们将使用…...
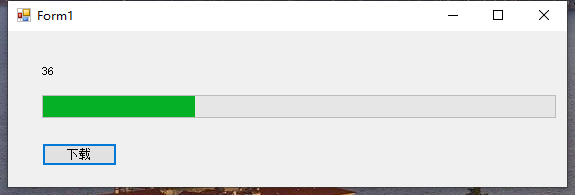
C#【必备技能篇】Winform跨线程更新进度条的实例
文章目录实例一:【方便理解,常用!】源码:运行效果:实例二:【重在理解代码本身】源码:运行效果:参考:实例一:【方便理解,常用!】 跨线…...

(1分钟速通面试) 矩阵分解相关内容
矩阵分解算法--总结QR分解 LU分解本篇博客总结一下QR分解和LU分解,这些都是矩阵加速的操作,在slam里面还算是比较常用的内容,这个地方在isam的部分出现过。(当然isam也是一个坑,想要出点创新成果的话 可能是不太现实的 短期来讲 哈…...

this指向
(1)在全局环境中的this——window 无论是否在严格模式下,在全局执行环境中(在任何函数体外部)this 都指向全局对象。 "use strict"console.log(this); //windowconsole.log(thiswindow);//true (…...

安卓小游戏:小板弹球
安卓小游戏:小板弹球 前言 这个是通过自定义View实现小游戏的第三篇,是小时候玩的那种五块钱的游戏机上的,和俄罗斯方块很像,小时候觉得很有意思,就模仿了一下。 需求 这里的逻辑就是板能把球弹起来,球…...
7、单行函数
文章目录1 函数的理解1.1 什么是函数1.2 不同DBMS函数的差异1.3 MySQL的内置函数及分类2 数值函数2.1 基本函数2.2 角度与弧度互换函数2.3 三角函数2.4 指数与对数2.5 进制间的转换3 字符串函数4 日期和时间函数4.1 获取日期、时间4.2 日期与时间戳的转换4.3 获取月份、星期、星…...
)
华为机试题:HJ56 完全数计算(python)
文章目录博主精品专栏导航知识点详解1、input():获取控制台(任意形式)的输入。输出均为字符串类型。1.1、input() 与 list(input()) 的区别、及其相互转换方法2、print() :打印输出。3、整型int() :将指定进制…...

opencv——傅里叶变换、低通与高通滤波及直方图等操作
1、傅里叶变换a、傅里叶变换原理时域分析:以时间为参照进行分析。频域分析:相当于上帝视角一样,看事物层次更高,时域的运动在频域来看就是静止的。eg:投球——时域分析:第1分钟投了3分,第2分钟投…...

网络六边形受到攻击
大家读完觉得有帮助记得关注和点赞!!! 抽象 现代智能交通系统 (ITS) 的一个关键要求是能够以安全、可靠和匿名的方式从互联车辆和移动设备收集地理参考数据。Nexagon 协议建立在 IETF 定位器/ID 分离协议 (…...

Spark 之 入门讲解详细版(1)
1、简介 1.1 Spark简介 Spark是加州大学伯克利分校AMP实验室(Algorithms, Machines, and People Lab)开发通用内存并行计算框架。Spark在2013年6月进入Apache成为孵化项目,8个月后成为Apache顶级项目,速度之快足见过人之处&…...

iPhone密码忘记了办?iPhoneUnlocker,iPhone解锁工具Aiseesoft iPhone Unlocker 高级注册版分享
平时用 iPhone 的时候,难免会碰到解锁的麻烦事。比如密码忘了、人脸识别 / 指纹识别突然不灵,或者买了二手 iPhone 却被原来的 iCloud 账号锁住,这时候就需要靠谱的解锁工具来帮忙了。Aiseesoft iPhone Unlocker 就是专门解决这些问题的软件&…...

解锁数据库简洁之道:FastAPI与SQLModel实战指南
在构建现代Web应用程序时,与数据库的交互无疑是核心环节。虽然传统的数据库操作方式(如直接编写SQL语句与psycopg2交互)赋予了我们精细的控制权,但在面对日益复杂的业务逻辑和快速迭代的需求时,这种方式的开发效率和可…...

Nuxt.js 中的路由配置详解
Nuxt.js 通过其内置的路由系统简化了应用的路由配置,使得开发者可以轻松地管理页面导航和 URL 结构。路由配置主要涉及页面组件的组织、动态路由的设置以及路由元信息的配置。 自动路由生成 Nuxt.js 会根据 pages 目录下的文件结构自动生成路由配置。每个文件都会对…...

CocosCreator 之 JavaScript/TypeScript和Java的相互交互
引擎版本: 3.8.1 语言: JavaScript/TypeScript、C、Java 环境:Window 参考:Java原生反射机制 您好,我是鹤九日! 回顾 在上篇文章中:CocosCreator Android项目接入UnityAds 广告SDK。 我们简单讲…...

从零实现STL哈希容器:unordered_map/unordered_set封装详解
本篇文章是对C学习的STL哈希容器自主实现部分的学习分享 希望也能为你带来些帮助~ 那咱们废话不多说,直接开始吧! 一、源码结构分析 1. SGISTL30实现剖析 // hash_set核心结构 template <class Value, class HashFcn, ...> class hash_set {ty…...

unix/linux,sudo,其发展历程详细时间线、由来、历史背景
sudo 的诞生和演化,本身就是一部 Unix/Linux 系统管理哲学变迁的微缩史。来,让我们拨开时间的迷雾,一同探寻 sudo 那波澜壮阔(也颇为实用主义)的发展历程。 历史背景:su的时代与困境 ( 20 世纪 70 年代 - 80 年代初) 在 sudo 出现之前,Unix 系统管理员和需要特权操作的…...

【笔记】WSL 中 Rust 安装与测试完整记录
#工作记录 WSL 中 Rust 安装与测试完整记录 1. 运行环境 系统:Ubuntu 24.04 LTS (WSL2)架构:x86_64 (GNU/Linux)Rust 版本:rustc 1.87.0 (2025-05-09)Cargo 版本:cargo 1.87.0 (2025-05-06) 2. 安装 Rust 2.1 使用 Rust 官方安…...

【无标题】路径问题的革命性重构:基于二维拓扑收缩色动力学模型的零点隧穿理论
路径问题的革命性重构:基于二维拓扑收缩色动力学模型的零点隧穿理论 一、传统路径模型的根本缺陷 在经典正方形路径问题中(图1): mermaid graph LR A((A)) --- B((B)) B --- C((C)) C --- D((D)) D --- A A -.- C[无直接路径] B -…...
