VP记录:Codeforces Round 868 (Div. 2) A~D
传送门:CF
A题:A-characteristic
构造一个只有 1 , − 1 1,-1 1,−1的数组,满足乘积为 1 1 1的数对的个数为 k k k.
发现 n n n的范围很小,考虑直接暴力枚举数组中 1 1 1的个数,记为 i i i,那么对于1的所有数对来说,我们有 i ∗ ( i − 1 ) / 2 i*(i-1)/2 i∗(i−1)/2个,然后对于 − 1 -1 −1的个数也不难表示出为 n − i n-i n−i,然后此时的贡献为 ( n − i − 1 ) ∗ ( n − i ) / 2 (n-i-1)*(n-i)/2 (n−i−1)∗(n−i)/2,判断即可
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
#define root 1,n,1
#define ls rt<<1
#define rs rt<<1|1
#define lson l,mid,rt<<1
#define rson mid+1,r,rt<<1|1
inline ll read() {ll x=0,w=1;char ch=getchar();for(;ch>'9'||ch<'0';ch=getchar()) if(ch=='-') w=-1;for(;ch>='0'&&ch<='9';ch=getchar()) x=x*10+ch-'0';return x*w;
}
#define maxn 1000000
const double eps=1e-8;
#define int_INF 0x3f3f3f3f
#define ll_INF 0x3f3f3f3f3f3f3f3f
int main() {int T=read();while(T--) {int n=read(),k=read();int ans1=-1,ans2=-1;for(int i=1;i<=n;i++) {int j=n-i;if((i-1)*i/2+(j-1)*j/2==k) {ans1=i;ans2=j;break;}}if(ans1==-1) {cout<<"NO"<<endl;}else {cout<<"YES"<<endl;for(int i=1;i<=ans1;i++) {cout<<"1 ";}for(int i=1;i<=ans2;i++) {cout<<"-1 ";}cout<<endl;}}return 0;
}
B题:Sort with Step
因为我们只能调换相距为 k k k的数对,那么我们可以将这个数组分为几个轨道,每一个轨道上的数字可以进行交换,不在同一个轨道上的数字不能进行交换.那么假设我们需要进行交换,也肯定是交换不在自己应该在的轨道上的那两个数字.所以我们可以直接记录不在自己应该在的轨道上的数字的个数(记为 k k k).因为我们唯一能使最后序列满足的情况就是将所有数字换到他们应该在的地方.所以当 k k k等于 1 1 1的时候代表其不需要进行初步交换,反之则需要进行 k k k次交换.
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
#define root 1,n,1
#define ls rt<<1
#define rs rt<<1|1
#define lson l,mid,rt<<1
#define rson mid+1,r,rt<<1|1
inline ll read() {ll x=0,w=1;char ch=getchar();for(;ch>'9'||ch<'0';ch=getchar()) if(ch=='-') w=-1;for(;ch>='0'&&ch<='9';ch=getchar()) x=x*10+ch-'0';return x*w;
}
#define maxn 1000000
const double eps=1e-8;
#define int_INF 0x3f3f3f3f
#define ll_INF 0x3f3f3f3f3f3f3f3f
int a[maxn];
int main() {int T=read();while(T--) {int n=read(),k=read();for(int i=1;i<=n;i++) {a[i]=read();}int cnt=0;int pos=-1;for(int i=1;i<=n;i++) {if(abs(i-a[i])%k!=0) {cnt++;}}if(cnt==0) {cout<<0<<endl;}else {if(cnt==2) {cout<<1<<endl;}else {cout<<-1<<endl;}}}return 0;
}
C题:Strongly Composite
一道需要进行分解质因数的题目.首先我们发现b数组的乘积要和a数组一样.那么不妨将a数组中的乘积进行一个分解质因数,先预处理存起来.显然我们最终b数组的所有数字就是由这些质因数组合而成
然后我们考虑强复合的性质.我们贪心的去想,肯定是用最小个数的质因数来组成一个数字是最优的.所以此时我们有两种组合方式:
1.我们拿两个相同的数来组成一个数 b i bi bi,此时我们的 b i bi bi显然是一个平方数,因为其实由两个质数组合而成,所以此时 b i bi bi显然是一个强复合.
2.显然1方案是最优的方案(因为花费的数字最少).但是此方案需要相同的数字.在1的方案下我们用完了所有的相同的数字,那么此时我们剩下来的就是不同的数字了.我们此时会发现一个很有趣的性质,我们拿出三个质数(记为 i i i, j j j, k k k)乘起来显然是一个强复合.因为两个质数乘起来肯定是一个合数,然后三个质数乘起来显然也是一个合数.又因为质因数的性质,此时我们的因子就是 1 , i , j , k , i ∗ j , i ∗ k , j ∗ k , i ∗ j ∗ k 1,i,j,k,i*j,i*k,j*k,i*j*k 1,i,j,k,i∗j,i∗k,j∗k,i∗j∗k,发现恰好是一个强复合数
至此本题也就不难解决了.
本部分介绍一下质因数分解算法的证明,如果熟悉的可以跳过:
for(int j=2;j<=__builtin_sqrt(a[i]);j++) {while(temp%j==0) {mp[j]++;temp/=j;}
}
if(temp!=1) mp[temp]++;
不难发现上述算法只判断到了 n \sqrt{n} n.下面证明一下这个算法的正确性.
首先证明这么做的得到的所有 j j j都是质数:
对于本部分采用反证法进行证明,假设我们当前枚举到的因子 j j j不是一个质数,那么他肯定是一个合数.此时根据唯一分解定理, j j j可以分解成 p 1 k 1 ∗ p 2 k 2 ∗ . . . ∗ p n k n p_1^{k_1}*p_2^{k_2}*...*p_n^{k_n} p1k1∗p2k2∗...∗pnkn这样的形式,那么必然存在 p i < j p_i<j pi<j,但是这样的因子我们在之前枚举到 p i p_i pi时的 w h i l e ( t e m p % j = = 0 ) while(temp\%j==0) while(temp%j==0)已经消掉了,所以不存在这种情况,所以 j j j必然是一个质数
接下来证明一下为什么只需要枚举到 n \sqrt{n} n,也就是证明一下最后剩下来的那个数字要么是1要么是一个大于 n \sqrt{n} n的质数
同样采取反证法进行证明,假设最后存在的那个数字k是一个大于 n \sqrt{n} n的合数.那么根据之前的证明我们会发现这个合数必然是不存在小于 n \sqrt{n} n的因子的.又因为他是一个合数,所以必然有两个大于 n \sqrt{n} n的因子,但是此时两个因子相乘得到的数显然比 n n n大,这是不合理的.所以最后剩下来的那个数必然是一个质数
至此证毕
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
#define root 1,n,1
#define ls rt<<1
#define rs rt<<1|1
#define lson l,mid,rt<<1
#define rson mid+1,r,rt<<1|1
inline ll read() {ll x=0,w=1;char ch=getchar();for(;ch>'9'||ch<'0';ch=getchar()) if(ch=='-') w=-1;for(;ch>='0'&&ch<='9';ch=getchar()) x=x*10+ch-'0';return x*w;
}
#define int long long
#define maxn 1000000
const double eps=1e-8;
#define int_INF 0x3f3f3f3f
#define ll_INF 0x3f3f3f3f3f3f3f3f
int a[maxn];map<int,int>mp;
map<int,int>mp2;
signed main() {int T=read();while(T--) {int n=read();mp.clear();mp2.clear();ll sum=1;int cnt=0;int ans=0;for(int i=1;i<=n;i++) {a[i]=read();int temp=a[i];if(a[i]==1) continue;for(int j=2;j<=__builtin_sqrt(a[i]);j++) {while(temp%j==0) {mp[j]++;temp/=j;}} if(temp!=1) mp[temp]++;}for(auto it : mp) {ans+=it.second/2;mp[it.first]=it.second-it.second/2*2;}for(auto it : mp) {cnt+=it.second;}ans+=cnt/3;cout<<ans<<endl;}return 0;
}
D题:Unique Palindromes
首先我们需要知道这样的一个事实,也就是我们每一次在一个字符串的后缀中加上一个任意字符a,我们的回文子串的增加个数最大为1.
简单证明一下这个结论:
我们假设现在有一个字符串为 s s s,那么假设我们此时加上一个 a a a使其增加了回文子串的个数.因为子串是连续的,所以此时我们不妨设多出了两个回文子串 s 1 + a , s 2 + a s1+a,s2+a s1+a,s2+a,并且 s 2 s2 s2是 s 1 s1 s1的后缀.不难发现 s 1 + a s1+a s1+a包含了 s 2 + a s2+a s2+a,又因为 s 1 + a s1+a s1+a是一个回文串,所以 s 2 + a s2+a s2+a既是 s 1 + a s1+a s1+a的后缀又是它的前缀.那么此时要么 s 2 + a = = s 1 + a s2+a==s1+a s2+a==s1+a,要么 s 2 + a s2+a s2+a是被 s 2 s2 s2包含的.因为当 s 2 + a s2+a s2+a的长度小于 s 1 + a s1+a s1+a时,又因为是前缀,显然它是被 s 2 s2 s2包含的, s 2 + a s2+a s2+a的长度又不可能大于 s 1 + a s1+a s1+a
至此证毕
所以显然当存在 c [ i ] − c [ i − 1 ] > x [ i ] − x [ i − 1 ] c[i]-c[i-1]>x[i]-x[i-1] c[i]−c[i−1]>x[i]−x[i−1]时我们是无法构造的.此处特判一下
然后我们考虑构造,因为ci>3.所以考虑将"abc"作为前缀,当我们此时的c1不够时不断的补上字符"c"来使得其满足.可能会存在回文子串够了但是长度不够的情况.所以我们此时需要补上后缀.此时我们可以反复的补上"abc".举个简单的栗子:
a b c c c ∣ a b c a b c a abccc\;|\; abcabca abccc∣abcabca,此时我们会很神奇的发现这样就不会增加回文子串了.
然后我们遇到了后面的回文条件.为了不会和前面已有的字符形成回文子串,我们考虑使用新的字符即可,比如 d , e , f . . . d,e,f... d,e,f....我们发现k<20.所以我们的26个字符是够用的.每一次多增加一个字符我们就可以得到一个贡献,当我们的贡献满时继续使用"abc"填满即可.
注意此时有一个小细节,我们此时的填充需要继续上述的循环,不然可能出现下述情况:ccc ∣ \;|\; ∣abca ∣ \;|\; ∣dda,我们会发现会导致意外增加了一个回文子串.
光讲可能比较难以理解,建议结合代码食用
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
#define root 1,n,1
#define ls rt<<1
#define rs rt<<1|1
#define lson l,mid,rt<<1
#define rson mid+1,r,rt<<1|1
inline ll read() {ll x=0,w=1;char ch=getchar();for(;ch>'9'||ch<'0';ch=getchar()) if(ch=='-') w=-1;for(;ch>='0'&&ch<='9';ch=getchar()) x=x*10+ch-'0';return x*w;
}
#define maxn 1000000
const double eps=1e-8;
#define int_INF 0x3f3f3f3f
#define ll_INF 0x3f3f3f3f3f3f3f3f
int x[maxn],c[maxn];
int main() {int T=read();while(T--) {int n=read(),k=read();for(int i=1;i<=k;i++) x[i]=read();for(int i=1;i<=k;i++) c[i]=read();int flag=0;for(int i=1;i<=k;i++) {if(c[i]-c[i-1]>x[i]-x[i-1]) {flag=1;break;}}if(flag==1) {cout<<"NO"<<endl;continue;}vector<char>ans;char kkk='c';ans.push_back('a');ans.push_back('b');ans.push_back('c');int pos=4;int hhh=3;char loop='a';for(int i=1;i<=k;i++) {if(i==1) {while(pos<=x[i]) {if(pos<=c[i]) {ans.push_back('c');}else {ans.push_back(loop);loop++;if(loop=='d') loop='a';}pos++;}}else{while(pos<=x[i]) {if(x[i]-pos+1>c[i]-c[i-1]) {//先达成条件再补长度ans.push_back(loop);loop++;if(loop=='d') loop='a';}else {ans.push_back('c'+i-1);}pos++;}}}cout<<"YES"<<endl;for(int i=0;i<ans.size();i++) cout<<ans[i];cout<<endl;}return 0;
}
相关文章:
 A~D)
VP记录:Codeforces Round 868 (Div. 2) A~D
传送门:CF A题:A-characteristic 构造一个只有 1 , − 1 1,-1 1,−1的数组,满足乘积为 1 1 1的数对的个数为 k k k. 发现 n n n的范围很小,考虑直接暴力枚举数组中 1 1 1的个数,记为 i i i,那么对于1的所有数对来说,我们有 i ∗ ( i − 1 ) / 2 i*(i-1)/2 i∗(i−1)/2个,然后…...

【VQ-VAE-2论文精读】Generating Diverse High-Fidelity Images with VQ-VAE-2
【VQ-VAE-2论文精读】Generating Diverse High-Fidelity Images with VQ-VAE-2 0、前言Abstract1 Introduction2 Background2.1 Vector Quantized Variational AutoEncoder3 Method3.1 Stage 1: Learning Hierarchical Latent Codes3.2 Stage 2: Learning Priors over Latent C…...
并发编程基石:管程
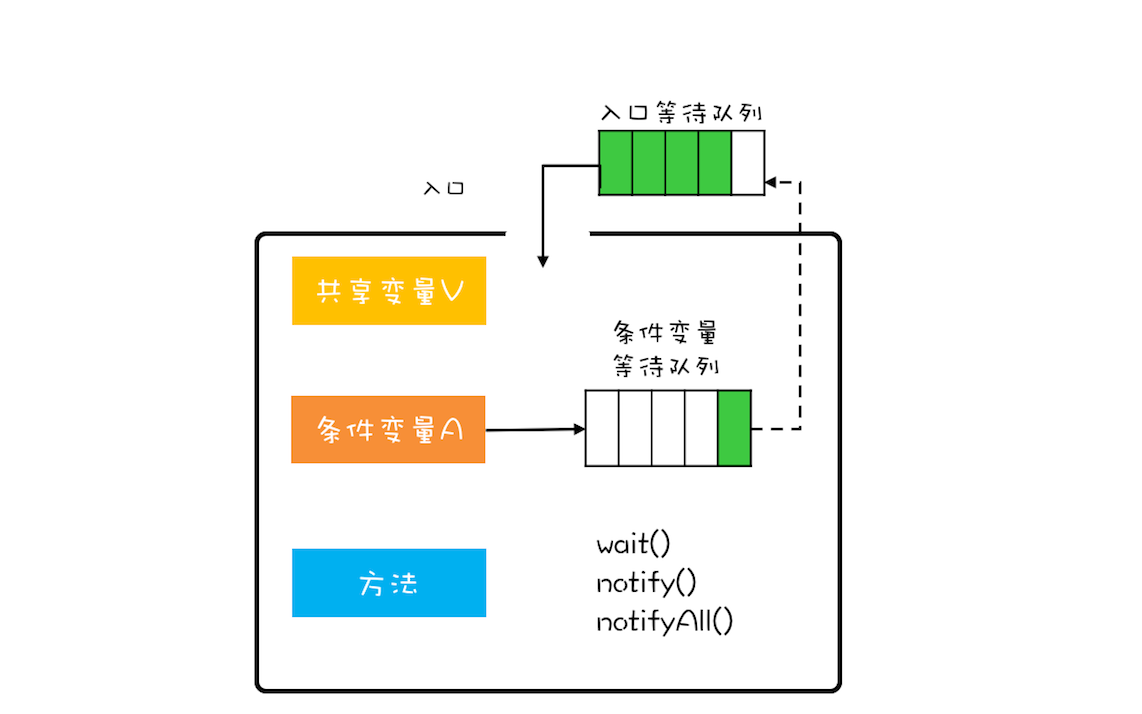
大家好,我是易安! 如果有人问我学习并发并发编程,最核心的技术点是什么,我一定会告诉他,管程技术。Java语言在1.5之前,提供的唯一的并发原语就是管程,而且1.5之后提供的SDK并发包,也…...
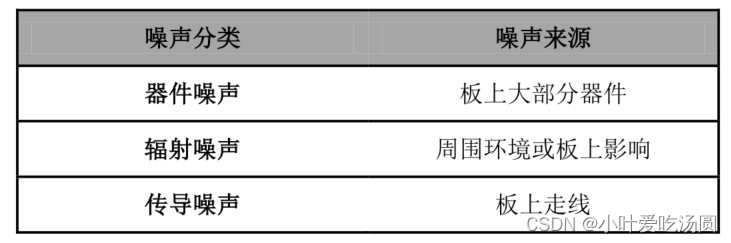
电路中噪声来源
电路包括不同的部件和芯片,所有都有可能成为噪声的来源。例如,电阻会带来热噪声,这个噪声为宽频噪声,几乎涵盖所有频率范围;运算放大器其芯片内部会产生噪声;而 ADC产生的量化噪声相较于其他器件࿰…...

JAVASE的全面总结
(未完待续) 五、子类与继承 5.1 子类与父类 继承是一种由已有的类创建新类的机制。利用继承,我们可以先创建一个共有属性的一般类,根据该一般类再创建具有特殊属性的新类,新类继承一般类的状态和行为,并…...
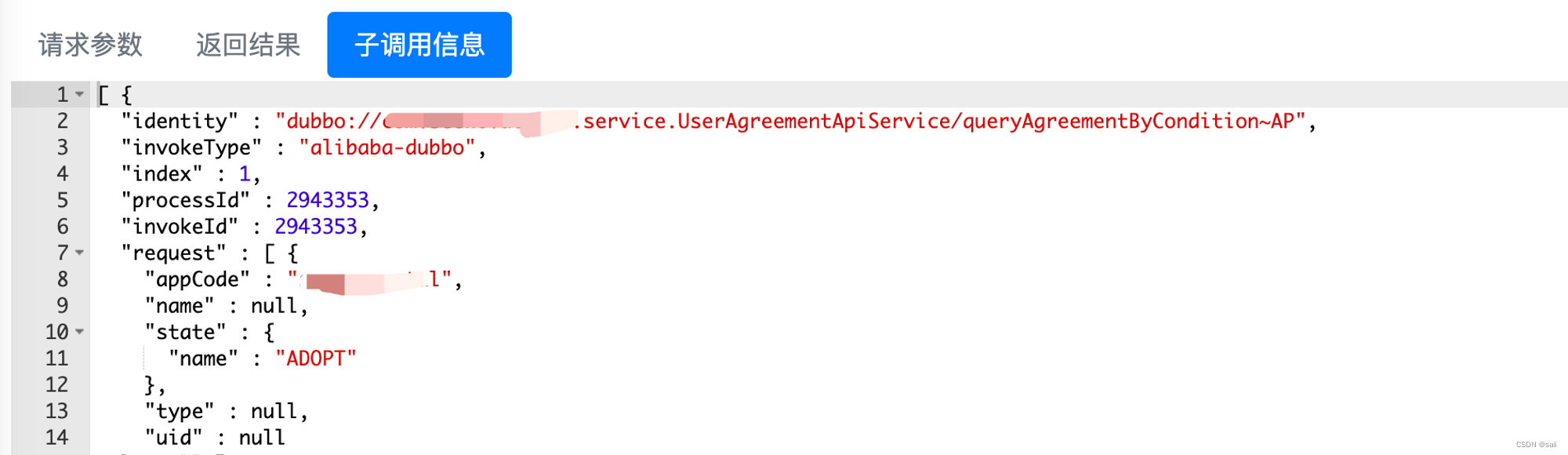
关于repeater录制的流量子调用的identity中带有~S的情况
前段时间同事问我,我们录制的流量中,尤其是dubbo的子调用显示经常他的末尾会带上一个小尾巴这个是什么意思呢,其实之前我没有太在意这个事情,只是同事这么疑问了,确实激起了好奇心,所以就差了下 到底是什么…...

Java面试题队列
Java中的队列都有哪些,有什么区别 1. ArrayDeque, (数组双端队列) 2. PriorityQueue, (优先级队列) 3. ConcurrentLinkedQueue, (基于链表的并发队列) 4. DelayQueue, (延期…...

大型Saas系统的权限体系设计(二)
X0 上期回顾 上文《大型Saas系统的权限体系设计(一)》提到2B的Saas系统的多层次权限体系设计的难题,即平台、平台的客户、客户的客户,乃至客户的客户的客户如何授权,这个可以通过“权限-角色-岗位”三级结构来实现。 但这个只是功能权限&am…...
HTML(四) -- 多媒体设计
目录 1. 视频标签 2. 音频标签 3. 资源标签(定义媒介资源 ) 1. 视频标签 属性值描述autoplayautoplay如果出现该属性,则视频在就绪后马上播放。controlscontrols表示添加标准的视频控制界面,包括播放、暂停、快进、音量等…...
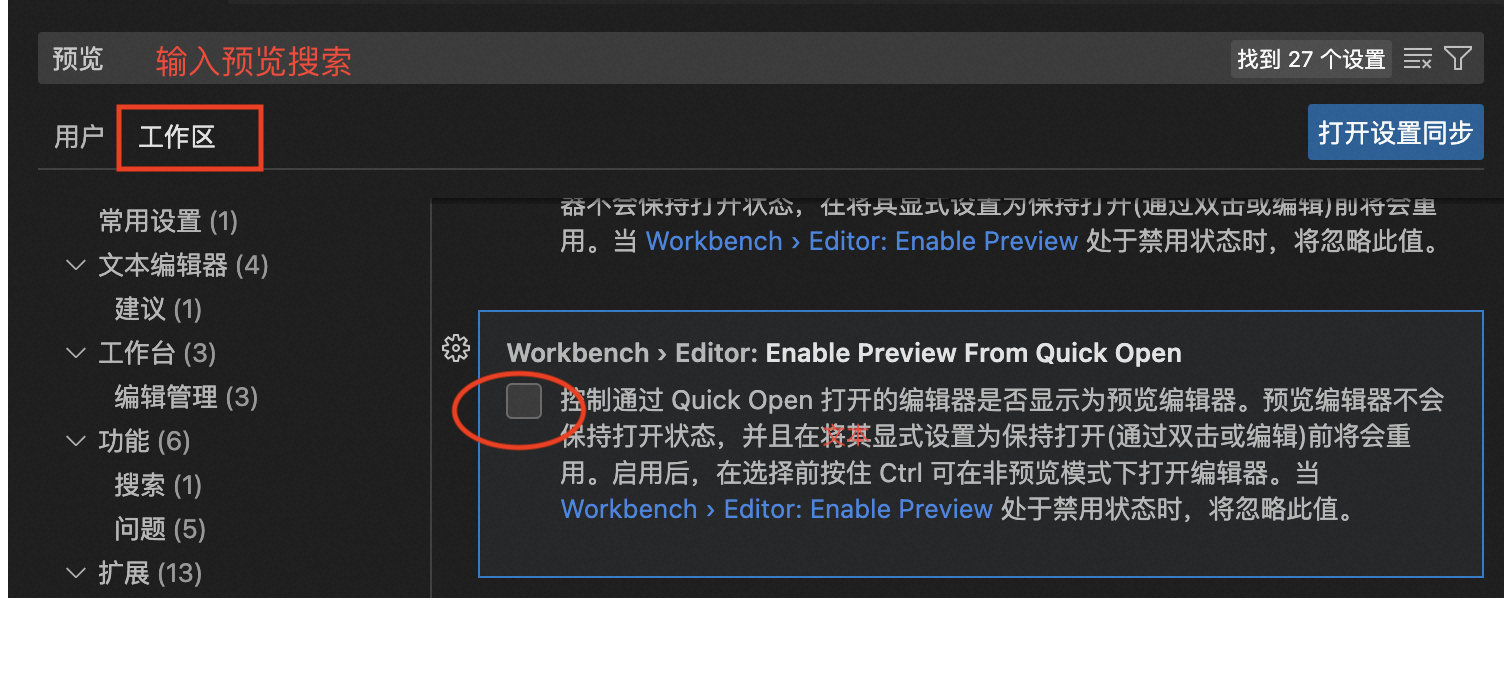
设置苹果电脑vsode在新窗口中打开文件
0、前言 最近切换到mac电脑工作,又得重新安装一些工具软件并设置。虽然这些设置并表示啥复杂的设置,但是久了不设置还是会忘记。于是记录之,也希望给能帮助到需要的人。 我们使用vscode阅读或者编辑文件时,有时候希望同时打开多…...

第二章创建模式—单例设计模式
文章目录 单例模式的结构如何控制只有一个对象呢怎么设计这个类的内部对象外部怎么访问 单例模式的主要有以下角色 单例模式的实现饿汉式 1:静态变量饿汉式 2:静态代码块懒汉式 1:线程不安全懒汉式 2:线程安全—方法级上锁懒汉式 …...
数据结构学习记录——堆的插入(堆的结构类型定义、最大堆的创建、堆的插入:堆的插入的三种情况、哨兵元素)
目录 堆的结构类型定义 最大堆的创建 堆的插入 堆的插入的三种情况 代码实现 哨兵元素 堆的结构类型定义 #define ElementType int typedef struct HNode* Heap; /* 堆的类型定义 */ struct HNode {ElementType* Data; /* 存储元素的数组 */int Size; /* 堆中…...

netperf测试
netperf测试 目录 批量网络流量性能测试 TCP_STREAM测试UDP_STREAM 测试请求/应答网络流量测试 TCP_RR TCP_CRR Netperf 是一个网络性能测试工具,它可以测试网络协议栈的性能,例如TCP和UDP协议。Netperf可以测量网络吞吐量、延迟和CPU利用率等指标。…...

ORACLE常用语句
1.修改用户密码 alter user 用户名 identified by 新密码; 2.表空间扩容 1.增加数据文件 alter tablespace AA add datafile ‘DATA’ size 20G autoextend off; 2.修改数据文件大小 ALTER DATABASE DATAFILE ‘E:\ORACLE\PRODUCT\10.2.0\ORADATA\aa\aa.DBF’ RESIZE 400M;…...
[论文笔记]C^3F,MCNN:图片人群计数模型
(万能代码)CommissarMa/Crowd_counting_from_scratch 代码:https://github.com/CommissarMa/Crowd_counting_from_scratch (万能代码)C^3 Framework开源人群计数框架 科普中文博文:https://zhuanlan.zhihu.com/p/65650998 框架网址:https…...
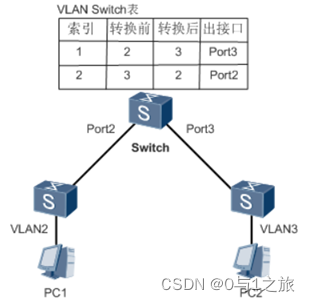
HCIP-7.2VLAN间通信单臂、多臂、三层交换方式学习
VLAN间通信单臂、多臂、三层交换方式学习 1、单臂路由2、多臂路由3、三层交换机的SVI接口实现VLAN间通讯3.1、VLANIF虚拟接口3.2、VLAN间路由3.2.1、单台三层路由VLAN间通信,在一台三层交换机内部VLAN之间直连。3.2.2、两台三层交换机的之间的VLAN通信。3.2.3、将物…...

PHP快速入门17-用spl_autoload_register实现类的自动加载
文章目录 前言实现过程创建两个类创建入口文件 总结 前言 本文已收录于PHP全栈系列专栏:PHP快速入门与实战 PHP类自动载入是指在PHP应用程序中,当需要使用某个类文件时,系统会自动加载该类文件,无需手动引入。 在PHP中…...
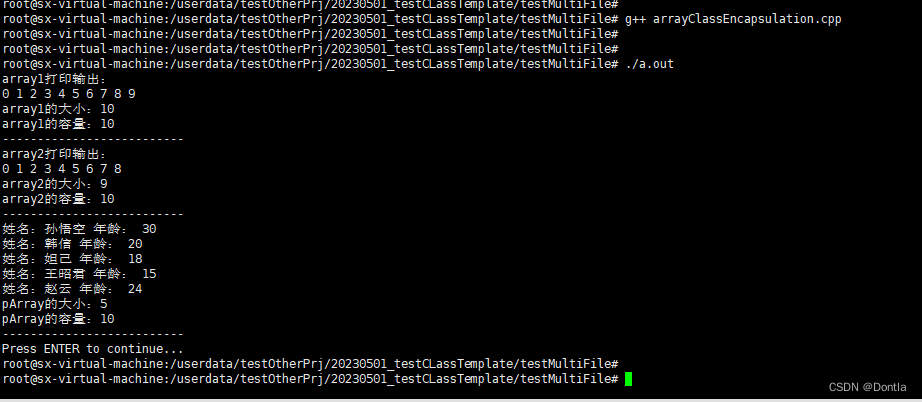
【黑马程序员 C++教程从0到1入门编程】【笔记8】 泛型编程——模板
https://www.bilibili.com/video/BV1et411b73Z?p167 C泛型编程是一种编程范式,它的核心思想是编写通用的代码,使得代码可以适用于多种不同的数据类型。 而模板是C中实现泛型编程的一种机制,它允许我们编写通用的代码模板,然后在需…...
分享10个精美可视化模板,解决95%的大屏需求!
前段时间和朋友一起喝茶,我吐槽着excel表格做报表的繁琐,他惊讶的问我竟然不知道大屏模板这种东西,说是直接套用数据就可以,我震惊的同时吃下了这个安利。 回来之后,我好好研究了一番这个叫可视化大屏的“新鲜玩意儿”…...

好用的项目管理软件的具体功能有哪些
随着企业规模不断的扩大,项目管理往往会面临更多的挑战与难题,最常见的会出现以下几个问题:资源消耗失控,而项目部门和相关部门之间沟通越来越困难;团队凝聚力下降、项目进度难以把控,项目成本几乎失控&…...

python打卡day49
知识点回顾: 通道注意力模块复习空间注意力模块CBAM的定义 作业:尝试对今天的模型检查参数数目,并用tensorboard查看训练过程 import torch import torch.nn as nn# 定义通道注意力 class ChannelAttention(nn.Module):def __init__(self,…...

微软PowerBI考试 PL300-选择 Power BI 模型框架【附练习数据】
微软PowerBI考试 PL300-选择 Power BI 模型框架 20 多年来,Microsoft 持续对企业商业智能 (BI) 进行大量投资。 Azure Analysis Services (AAS) 和 SQL Server Analysis Services (SSAS) 基于无数企业使用的成熟的 BI 数据建模技术。 同样的技术也是 Power BI 数据…...

关于nvm与node.js
1 安装nvm 安装过程中手动修改 nvm的安装路径, 以及修改 通过nvm安装node后正在使用的node的存放目录【这句话可能难以理解,但接着往下看你就了然了】 2 修改nvm中settings.txt文件配置 nvm安装成功后,通常在该文件中会出现以下配置&…...

LeetCode - 394. 字符串解码
题目 394. 字符串解码 - 力扣(LeetCode) 思路 使用两个栈:一个存储重复次数,一个存储字符串 遍历输入字符串: 数字处理:遇到数字时,累积计算重复次数左括号处理:保存当前状态&a…...

对WWDC 2025 Keynote 内容的预测
借助我们以往对苹果公司发展路径的深入研究经验,以及大语言模型的分析能力,我们系统梳理了多年来苹果 WWDC 主题演讲的规律。在 WWDC 2025 即将揭幕之际,我们让 ChatGPT 对今年的 Keynote 内容进行了一个初步预测,聊作存档。等到明…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一)
宇树机器人多姿态起立控制强化学习框架论文解析 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一) 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化…...
)
相机Camera日志分析之三十一:高通Camx HAL十种流程基础分析关键字汇总(后续持续更新中)
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了:有对最普通的场景进行各个日志注释讲解,但相机场景太多,日志差异也巨大。后面将展示各种场景下的日志。 通过notepad++打开场景下的日志,通过下列分类关键字搜索,即可清晰的分析不同场景的相机运行流程差异…...

重启Eureka集群中的节点,对已经注册的服务有什么影响
先看答案,如果正确地操作,重启Eureka集群中的节点,对已经注册的服务影响非常小,甚至可以做到无感知。 但如果操作不当,可能会引发短暂的服务发现问题。 下面我们从Eureka的核心工作原理来详细分析这个问题。 Eureka的…...

安宝特方案丨船舶智造的“AR+AI+作业标准化管理解决方案”(装配)
船舶制造装配管理现状:装配工作依赖人工经验,装配工人凭借长期实践积累的操作技巧完成零部件组装。企业通常制定了装配作业指导书,但在实际执行中,工人对指导书的理解和遵循程度参差不齐。 船舶装配过程中的挑战与需求 挑战 (1…...

【C++进阶篇】智能指针
C内存管理终极指南:智能指针从入门到源码剖析 一. 智能指针1.1 auto_ptr1.2 unique_ptr1.3 shared_ptr1.4 make_shared 二. 原理三. shared_ptr循环引用问题三. 线程安全问题四. 内存泄漏4.1 什么是内存泄漏4.2 危害4.3 避免内存泄漏 五. 最后 一. 智能指针 智能指…...
