【VAR | 时间序列】应用VAR模型时的15个注意点
一、前言
向量自回归(VAR,Vector Auto regression)常用于预测相互联系的时间序列系统以及分析随机扰动对变量系统的动态影响。
VAR方法通过把系统中每一个内生变量,作为系统中所有内生变量的滞后值的函数来构造模型,从而回避了结构化模型的要求。
Engle和Granger(1987)指出两个或多个非平稳时间序列的线性组合可能是平稳的。假如这样一种平稳的或的线性组合存在,这些非平稳(有单位根)时间序列之间被认为是具有协整关系的。这种平稳的线性组合被称为协整方程且可被解释为变量之间的长期均衡关系。
VAR模型对于相互联系的时间序列变量系统是有效的预测模型,同时,向量自回归模型也被频繁地用于分析不同类型的随机误差项对系统变量的动态影响。如果变量之间不仅存在滞后影响,而不存在同期影响关系,则适合建立VAR模型,因为VAR模型实际上是把当期关系隐含到了随机扰动项之中。
二、注意点
- 单位根检验是序列的平稳性检验,如果不检验序列的平稳性直接OLS容易导致伪回归。
- 当检验的数据是平稳的(即不存在单位根),要想进一步考察变量的因果联系,可以采用格兰杰因果检验,但要做格兰杰检验的前提是数据必须是平稳的,否则不能做。
- 当检验的数据是非平稳(即存在单位根),并且各个序列是同阶单整(协整检验的前提),想进一步确定变量之间是否存在协整关系,可以进行协整检验,协整检验主要有EG两步法和JJ检验。
EG两步法是基于回归残差的检验,可以通过建立OLS模型检验其残差平稳性;
JJ检验是基于回归系数的检验,前提是建立VAR模型(即模型符合ADL模式)。
- 当变量之间存在协整关系时,可以建立ECM进一步考察短期关系,Eviews这里还提供了一个Wald-Granger检验,但此时的格兰杰已经不是因果关系检验,而是变量外生性检验,请注意识别。
- 格兰杰检验只能用于平稳序列!这是格兰杰检验的前提,而其因果关系并非我们通常理解的因与果的关系,而是说x的前期变化能有效地解释y的变化,所以称其为“格兰杰原因”。
- 非平稳序列很可能出现伪回归,协整的意义就是检验它们的回归方程所描述的因果关系是否是伪回归,即检验变量之间是否存在稳定的关系。所以,非平稳序列的因果关系检验就是协整检验。
- 平稳性检验有3个作用:1)检验平稳性,若平稳,做格兰杰检验,非平稳,作协正检验。2)协整检验中要用到每个序列的单整阶数。3)判断时间学列的数据生成过程。
ADF检验:
(1)view—unit root test,出现对话框,默认的选项为变量的原阶序列检验平稳性,确认后,若ADF检验的P值小于0.05,拒绝原假设,说明序列是平稳的,若P值大于0.5,接受原假设,说明序列是非平稳的;
(2)重复刚才的步骤,view—unit root test,出现对话框,选择1st difference,即对变量的一阶差分序列做平稳性检验,和第一步中的检验标准相同,若P值小于5%,说明是一阶平稳,若P值大于5%,则继续进行二阶差分序列的平稳性检验。
先做单位根检验,看变量序列是否平稳序列,若平稳,可构造回归模型等经典计量经济学模型;
若非平稳,进行差分,当进行到第i次差分时序列平稳,则服从i阶单整(注意趋势、截距不同情况选择,根据P值和原假设判定)。
若所有检验序列均服从同阶单整,可构造VAR模型,做协整检验(注意滞后期的选择),判断模型内部变量间是否存在协整关系,即是否存在长期均衡关系。如果有,则可以构造VEC模型或者进行Granger因果检验,检验变量之间“谁引起谁变化”,即因果关系。
第一,格兰杰因果检验是检验统计上的时间先后顺序,并不表示而这真正存在因果关系,是否呈因果关系需要根据理论、经验和模型来判定。
第二,格兰杰因果检验的变量应是平稳的,如果单位根检验发现两个变量是不稳定的,那么,不能直接进行格兰杰因果检验,所以,很多人对不平稳的变量进行格兰杰因果检验,这是错误的。
第三,协整结果仅表示变量间存在长期均衡关系,那么,到底是先做格兰杰还是先做协整呢?因为变量不平稳才需要协整,所以,首先因对变量进行差分,平稳后,可以用差分项进行格兰杰因果检验,来判定变量变化的先后时序,之后,进行协整,看变量是否存在长期均衡。
第四,长期均衡并不意味着分析的结束,还应考虑短期波动,要做误差修正检验。
- 单位根检验是检验数据的平稳性,或是说单整阶数。
- 协整是说两个或多个变量之间具有长期的稳定关系。但变量间协整的必要条件是它们之间是同阶单整,也就是说在进行协整检验之前必须进行单位跟检验。
- 协整说的是变量之间存在长期的稳定关系,这只是从数量上得到的结论,但不能确定谁是因,谁是果。而因果关系检验解决的就是这个问题。
单位根检验是检验时间序列是否平稳,协整是在时间序列平稳性的基础上做长期趋势的分析,而格兰杰检验一般是在建立误差修正模型的后,所建立的短期的因果关系。故顺序自然是先做单位根检验,再过协整检验,最后是格兰杰因果检验。
单位根检验是对时间序列平稳性的检验,只有平稳的时间序列,才能进行计量分析,否则会出现伪回归现象;协整是考察两个或者多个变量之间的长期平稳关系,考察两者的协整检验通常采用恩格尔–格兰杰检验,两者以上则用Johansen检验;格兰杰因果检验是考察变量之间的因果关系,协整说明长期稳定关系不一定是因果关系,所以需要在通过格兰杰因果检验确定两者的因果关系。顺序一般是单位根检验,通过后如果同阶单整,在进行协整,然后在进行因果检验。要特别注意的是:只有同阶单整才能进行协整。
- VAR建模时lag intervals for endogenous要填滞后期,但是此时你并不能判断哪个滞后时最优的,因此要试,选择不同的滞后期,至AIC或SC最小时,所对应着的滞后为最优滞后,此时做出来的VAR模型才较为可靠。
- 做协整检验前作VAR的原因是,协整检验是对滞后期和检验形式非常敏感的检验,首先需要确定最优滞后。由于VAR是无约束的,而协整是有约束的,因此协整检验的最优滞后一般为VAR的最优滞后减去1,确定了最优滞后后,再去诊断检验形式,最终才能做协整。
- 当确定了协整的个数后,往下看,有个标准化的结果,这个结果就是协整方程,由于在结果中各变量均在方程一侧,因此如果系数为正,则说明是负向关系,反之亦然。
- 协整表示变量间的长期均衡关系,貌似与OLS不矛盾。
(1)如检验不协整,说明没长期稳定关第,可以做VAR模型,但是模型建立后要做
稳定性分析:做AR根的图表分析,如所有单位根小于1,说明VAR模型定,满足脉冲分析及方差分解所需条件之一
模型的因果关系检验 2 不过注意在做因果检验前要先确定滞后长度,方法见高铁梅 计量分析方法与建模 第2版 P302 只有满足因果关系,加上满足条件一:稳定性,则可进行脉冲及方差分解
如不满足因果关系,则所有不满足因果关系的变量将视为外生变量 ,至此要重新构建VAR模型,新的VAR模型将要引入外生变量的VAR模型
(2)VAR与VEC关系是:VEC是有协整约束(即有长期稳定关系)的VAR模型,多用于具有协整关系的非平稳时间序列建模 高铁梅 计理分析方法与建模 第2版 P295
- 简单说VAR模型建立时
第一步:不问序列如何均可建立初步的VAR模型(建立过程中数据可能前平稳序列,也可能是部分平稳,还可能是没协整关系的同阶不平稳序列,也可能是不同阶的不平稳序列,滞后阶数任意指定。所有序列一般视为内生向量),
第二步:在建立的初步VAR后进行:
(1)滞后阶数检验,以确定最终模型的滞后阶数;
(2)在滞后阶数确定后进行因果关系检验,以确定哪些序列为外生变量。
至此重新构建VAR模型(此时滞后阶数已定,内外生变量已定),再进行AR根图表分析,如单位根均小于1,VAR构建完成可进行脉冲及方差分解;
如单位根有大于1的,考虑对原始序进行降阶处理(一阶单整序列处理方法:差分或取对数,二阶单整序列:理论上可以差分与取对数同时进行,但由于序列失去了经济含义,应放弃此处理,可考虑序列的趋势分解,如分解后仍然不能满足要求,可以罢工,不建立任何模型,休息或是打砸了电脑),处理过后对新的序列(包括最初的哪些平稳序列)不断重复第一步与第二步,直至满足稳定性为止。
第三步,建立最终的VAR后,可考虑SVAR模型。
如果变量不仅存在滞后影响,还存在同期影响关系,则建立VAR模型不太合适,这种情况下需要进行结构分析。
相关文章:

【VAR | 时间序列】应用VAR模型时的15个注意点
一、前言 向量自回归(VAR,Vector Auto regression)常用于预测相互联系的时间序列系统以及分析随机扰动对变量系统的动态影响。 VAR方法通过把系统中每一个内生变量,作为系统中所有内生变量的滞后值的函数来构造模型,从而回避了结构化模型的…...

校招在线测评题目汇总
图形找规律题 https://blog.csdn.net/mxj1428295019/article/details/129627461https://blog.csdn.net/Yujian2563/article/details/124266574?spm1001.2101.3001.6650.2&utm_mediumdistribute.pc_relevant.none-task-blog-2%7Edefault%7ECTRLIST%7ERate-2-124266574-blo…...

『python爬虫』05. requests模块入门(保姆级图文)
目录 安装requests1. 抓取搜狗搜索内容 requests.get2. 抓取百度翻译数据 requests.post3. 豆瓣电影喜剧榜首爬取4. 关于请求头和关闭request连接总结 欢迎关注 『python爬虫』 专栏,持续更新中 欢迎关注 『python爬虫』 专栏,持续更新中 安装requests …...

WPF超好用的框架Prism入门使用,上位机赶紧学起来!
Prism简介 WPF框架Prism是一种用于开发模块化、可重用和可测试的WPF应用程序的框架。它提供了一种简单而强大的方式来管理复杂应用程序的代码和构建高度可扩展的应用程序。 如何学习Prism框架 如果您想使用Prism框架来开发WPF应用程序,需要学习以下几个方面&…...

十个机器学习应用实例
一、在Kaggle上举办的一个竞赛,名为“Tabular Playground Series - Aug 2021”。该竞赛旨在预测房屋销售价格,数据集包含了79个特征和一个目标变量。参赛者需要训练一个模型,能够预测测试集中房屋的销售价格。 该竞赛的获胜者使用了多个AI模型…...

【Redis17】Redis进阶:管道
Redis进阶:管道 管道是啥?我们做开发的同学们经常会在 Linux 环境中用到管道命令,比如 ps -ef | grep php 。在之前学习 Laravel框架时的 【Laravel6.4】管道过滤器https://mp.weixin.qq.com/s/CK-mcinYpWCIv9CsvUNR7w 这篇文章中,…...
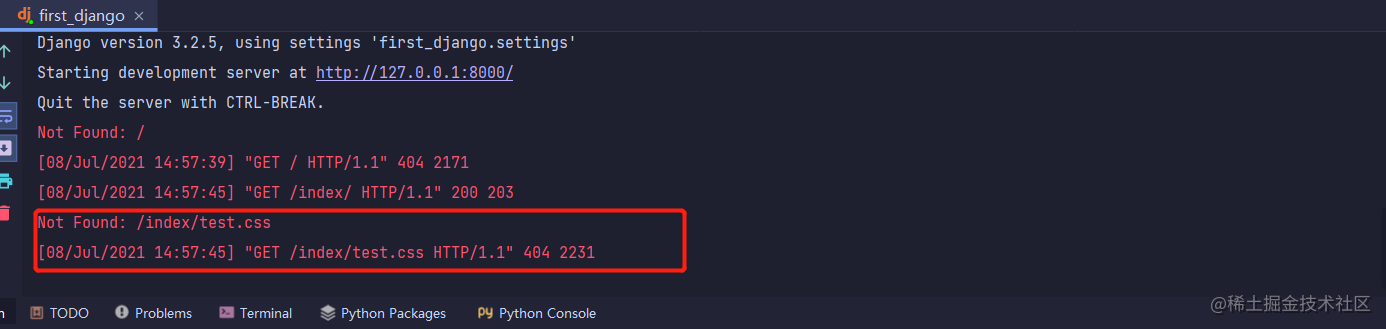
Django项目页面样式如何“传给”客户端浏览器
前言 django项目在视图函数中借助render函数可以返回HTML页面,但是HTML页面中如果引入了外部CSS文件或者JavaScript文件在浏览器页面无法加载,因此就必须有一种方式能够将HTML文档中引入的外部文件能够在客户端浏览器上加载,这种方式就是配置…...
、Pipe()、manager.list()、manager.dict()、manager.Queue())
python 进程间通信 Queue()、Pipe()、manager.list()、manager.dict()、manager.Queue()
👨💻个人简介: 深度学习图像领域工作者 🎉总结链接: 链接中主要是个人工作的总结,每个链接都是一些常用demo,代码直接复制运行即可。包括: &am…...
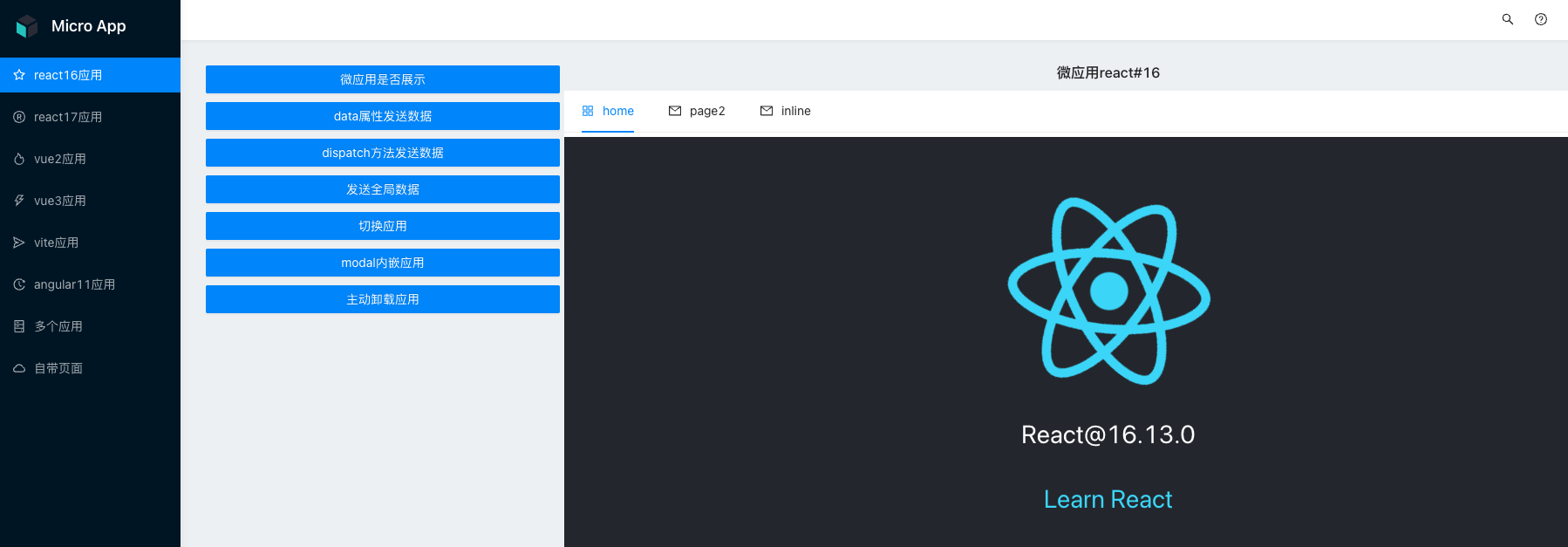
你想要的【微前端】都在这里了! | 京东云技术团队
作者:京东零售 郑炳懿 开篇: 如果你不知道微前端是什么,或者不知道微前端能解决什么问题,那么你可能不需要微前端。 在我看来,对于每一个没有使用过的新技术,都应该有以下几个过程: 1、调研…...
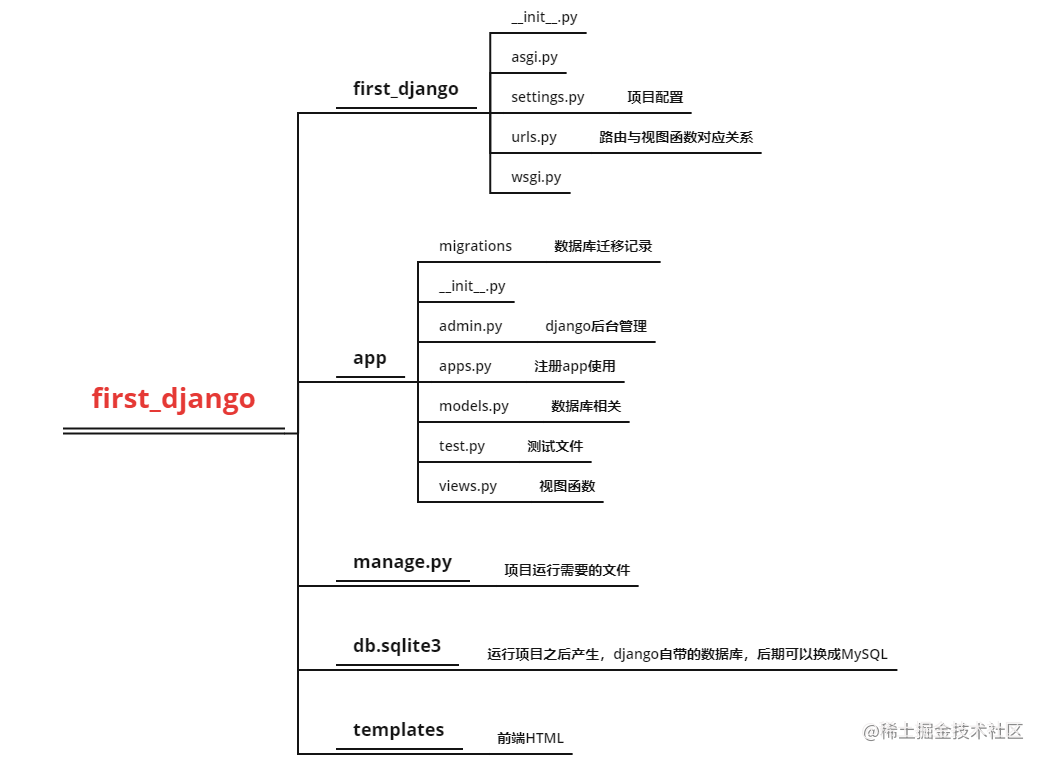
人生若只如初见,你不来看看Django吗
前言 本文介绍python三大主流web框架之一的Django框架的基本使用,如何创建django项目,如何运行django项目以及django项目的目录结构,另外django又是如何返回不同的数据和页面? python三大主流web框架 Python有三大主流的web框架…...

项目人力资源管理
项目人力资源管理的 4 个过程:规划人力资源管理、组建项目团队、建设项目团队、管理项目团队等内容 单项选择题、案例分析题 人力资源管理领域输入、输出、工具和技术表: 过程名输入工具和技术输出编写项目人力资源计划 项目管理计划活动资源需求事业…...

提供接口给第三方调用,应该注意什么
1.如果我们要提供一个接口给第三方调用,首先我们需要考虑的就是接口安全,一定要做鉴权,至于鉴权的方式:大家可以在网上自行查找,今天我主要记录如何编写一个既能能支持并发的,且不会影响到我们自身业务的的…...

ESL设计概述
前言 随着芯片面临着应用场景丰富多变、集成功能模块越来越多、片内通信及模块间接口越来越复杂、设计规模越来越大以及PPA要求越来越高的需求,芯片设计方法面临越来越大的挑战。架构的合理性、完备性和一致性很大程度上决定了芯片设计的成败。基于同样的I…...
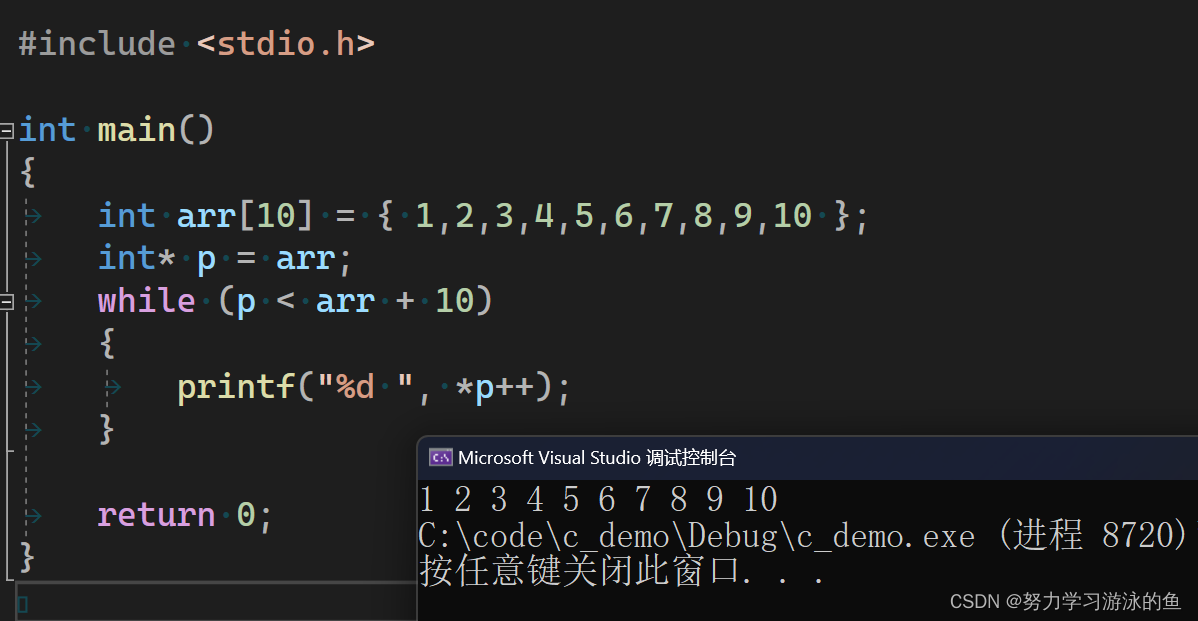
探究C语言数组的奥秘:大小可省略的定义、内存存储、数组名、传参、指针遍历、数组指针和指针数组、柔性数组等
也许你认为,C语言中的数组非常好理解,就是把一组相同类型的元素存储在同一块空间里。但是你可能并没有真正理解数组的本质,不信的话请回答一下下面的几个小问题,如果你能非常清晰的回答这些问题,那么你对C语言中的数组…...

python3 强制使用任意父级相对导入,越过python相对导入限制,拒绝 ImportError
前言 单纯不喜欢 python 对 点开头的包的限制,好麻烦,遂写了本包,来解决这个问题启用本模块后,你可以随时使用 单个点来导入当前目录的模块,也可以使用多个 点导入多级父目录内的模块,而不会报错烦人的模块…...
面了一个4年经验的测试工程师,自动化都不会也要15k,我也是醉了····
在深圳这家金融公司也待了几年,被别人面试过也面试过别人,大大小小的事情也见识不少,今天又是团面的一天, 一百多个人都聚集在一起,因为公司最近在谈项目出来面试就2个人,无奈又被叫到面试房间。 整个过程…...

Java 实现 YoloV7 人体姿态识别
1 OpenCV 环境的准备 这个项目中需要用到 opencv 进行图片的读取与处理操作,因此我们需要先配置一下 opencv 在 java 中运行的配置。 首先前往 opencv 官网下载 opencv-4.6 :点此下载;下载好后仅选择路径后即可完成安装。 此时将 opencv\b…...

跨越屏幕:桌面PC端的多端开发框架介绍
目前,随着互联网和移动互联网的发展,多端开发框架已经成为越来越多开发者更好的选择。主要有以下几个方面的前景: 跨平台开发需求不断增加:由于不同平台和设备的差异性,开发人员需要使用不同的编程语言和开发工具来为各…...

高效学习方法和工具推荐,让你事半功倍!
本文介绍了五种高效学习方法,包括制定详细的学习计划、集中注意力、不断复习、采用多种学习方式和利用小休息。同时,还推荐了五个高效学习工具和平台,包括Coursera、Duolingo、Quizlet、Khan Academy和Anki,让你在学习中事半功倍&…...

查看Docker容器中RabbitMQ的密码
要查看Docker容器中RabbitMQ的密码,可以尝试以下几个步骤: 1. 查看容器运行时的环境变量 在Docker容器中,可以通过环境变量来设置RabbitMQ的用户名和密码。因此,可以使用以下命令查看容器的环境变量: docker inspect…...

设计模式和设计原则回顾
设计模式和设计原则回顾 23种设计模式是设计原则的完美体现,设计原则设计原则是设计模式的理论基石, 设计模式 在经典的设计模式分类中(如《设计模式:可复用面向对象软件的基础》一书中),总共有23种设计模式,分为三大类: 一、创建型模式(5种) 1. 单例模式(Sing…...

大数据零基础学习day1之环境准备和大数据初步理解
学习大数据会使用到多台Linux服务器。 一、环境准备 1、VMware 基于VMware构建Linux虚拟机 是大数据从业者或者IT从业者的必备技能之一也是成本低廉的方案 所以VMware虚拟机方案是必须要学习的。 (1)设置网关 打开VMware虚拟机,点击编辑…...

连锁超市冷库节能解决方案:如何实现超市降本增效
在连锁超市冷库运营中,高能耗、设备损耗快、人工管理低效等问题长期困扰企业。御控冷库节能解决方案通过智能控制化霜、按需化霜、实时监控、故障诊断、自动预警、远程控制开关六大核心技术,实现年省电费15%-60%,且不改动原有装备、安装快捷、…...

IoT/HCIP实验-3/LiteOS操作系统内核实验(任务、内存、信号量、CMSIS..)
文章目录 概述HelloWorld 工程C/C配置编译器主配置Makefile脚本烧录器主配置运行结果程序调用栈 任务管理实验实验结果osal 系统适配层osal_task_create 其他实验实验源码内存管理实验互斥锁实验信号量实验 CMISIS接口实验还是得JlINKCMSIS 简介LiteOS->CMSIS任务间消息交互…...

华硕a豆14 Air香氛版,美学与科技的馨香融合
在快节奏的现代生活中,我们渴望一个能激发创想、愉悦感官的工作与生活伙伴,它不仅是冰冷的科技工具,更能触动我们内心深处的细腻情感。正是在这样的期许下,华硕a豆14 Air香氛版翩然而至,它以一种前所未有的方式&#x…...

SiFli 52把Imagie图片,Font字体资源放在指定位置,编译成指定img.bin和font.bin的问题
分区配置 (ptab.json) img 属性介绍: img 属性指定分区存放的 image 名称,指定的 image 名称必须是当前工程生成的 binary 。 如果 binary 有多个文件,则以 proj_name:binary_name 格式指定文件名, proj_name 为工程 名&…...

iview框架主题色的应用
1.下载 less要使用3.0.0以下的版本 npm install less2.7.3 npm install less-loader4.0.52./src/config/theme.js文件 module.exports {yellow: {theme-color: #FDCE04},blue: {theme-color: #547CE7} }在sass中使用theme配置的颜色主题,无需引入,直接可…...

git: early EOF
macOS报错: Initialized empty Git repository in /usr/local/Homebrew/Library/Taps/homebrew/homebrew-core/.git/ remote: Enumerating objects: 2691797, done. remote: Counting objects: 100% (1760/1760), done. remote: Compressing objects: 100% (636/636…...

用鸿蒙HarmonyOS5实现国际象棋小游戏的过程
下面是一个基于鸿蒙OS (HarmonyOS) 的国际象棋小游戏的完整实现代码,使用Java语言和鸿蒙的Ability框架。 1. 项目结构 /src/main/java/com/example/chess/├── MainAbilitySlice.java // 主界面逻辑├── ChessView.java // 游戏视图和逻辑├── …...

P10909 [蓝桥杯 2024 国 B] 立定跳远
# P10909 [蓝桥杯 2024 国 B] 立定跳远 ## 题目描述 在运动会上,小明从数轴的原点开始向正方向立定跳远。项目设置了 $n$ 个检查点 $a_1, a_2, \cdots , a_n$ 且 $a_i \ge a_{i−1} > 0$。小明必须先后跳跃到每个检查点上且只能跳跃到检查点上。同时࿰…...
