基于灰狼算法的极限学习机(ELM)回归预测-附代码
基于灰狼算法的极限学习机(ELM)回归预测
文章目录
- 基于灰狼算法的极限学习机(ELM)回归预测
- 1.极限学习机原理概述
- 2.ELM学习算法
- 3.回归问题数据处理
- 4.基于灰狼算法优化的ELM
- 5.测试结果
- 6.参考文献
- 7.Matlab代码
摘要:本文利用灰狼算法对极限学习机进行优化,并用于回归预测
1.极限学习机原理概述
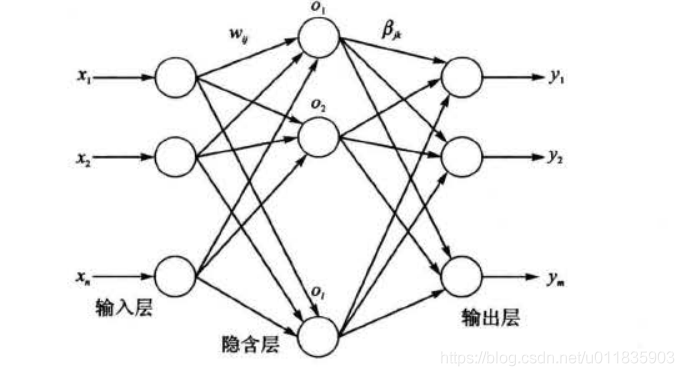
典型的单隐含层前馈神经网络结构如图1 所示,由输入层、隐含层和输出层组成,输 入层与隐含层、隐含层与输出层神经元间全连接。其中,输入层有 n 个神经元,对应 n 个输入变量, 隐含层有 l个神经元;输出层有 m 个神经元 ,对应 m 个输出变量 。 为不失一般性,设输 入层与隐含层间的连接权值 w 为:
w = [ w 11 w 12 . . . w 1 , n w 21 w 22 . . . w 2 n . . . w l 1 w l 2 . . . w l n ] (1) w =\left[\begin{matrix}w_{11}&w_{12}&...&w_{1,n}\\ w_{21}&w_{22}&...&w_{2n}\\ ...\\ w_{l1}&w_{l2}&...&w_{ln} \end{matrix}\right]\tag{1} w= w11w21...wl1w12w22wl2.........w1,nw2nwln (1)
其中, w n w_n wn表示输入层第 i i i个神经元与隐含层第 j j j个神经元间的连接权值。
设隐含层与输出层间的连接权值 , 为 β \beta β:
β = [ β 11 β 12 . . . β 1 m β 21 β 22 . . . β 2 m . . . β l 1 β l 2 . . . β l m ] (2) \beta =\left[\begin{matrix} \beta_{11}&\beta_{12}&...&\beta_{1m}\\ \beta_{21}&\beta_{22}&...&\beta_{2m}\\ ...\\ \beta_{l1}&\beta_{l2}&...&\beta_{lm} \end{matrix}\right] \tag{2} β= β11β21...βl1β12β22βl2.........β1mβ2mβlm (2)
其中,自 β j k \beta_{jk} βjk表示隐含层第 j 个神经元与输出层第 k个神经元间的连接权值。
设隐含层神经元的阈值值 b 为:
b = [ b 1 b 2 . . . b l ] (3) b =\left[\begin{matrix}b_1\\ b_2\\ ...\\ b_l \end{matrix}\right]\tag{3} b= b1b2...bl (3)
设具有 Q 个样本的训练集输入矩阵 X 和输出矩阵 Y 分别为
X = [ x 11 x 12 . . . x 1 Q x 21 x 22 . . . x 2 Q . . . x n 1 x n 2 . . . x n Q ] (4) X =\left[\begin{matrix}x_{11}&x_{12}&...&x_{1Q}\\ x_{21}&x_{22}&...&x_{2Q}\\ ...\\ x_{n1}&x_{n2}&...&x_{nQ} \end{matrix}\right]\tag{4} X= x11x21...xn1x12x22xn2.........x1Qx2QxnQ (4)
KaTeX parse error: Undefined control sequence: \matrix at position 11: Y =\left[\̲m̲a̲t̲r̲i̲x̲{y_{11},y_{12},…
设隐含层神经元的激活函数为 g(x),则由图1 可得, 网络的输出 T 为:
T = [ t 1 , . . , t Q ] m ∗ Q , t j = [ t 1 j , . . . , t m j ] T = [ ∑ i = 1 t β i 1 g ( w i x j + b i ) ∑ i = 1 t β i 2 g ( w i x j + b i ) . . . ∑ i = 1 t β i m g ( w i x j + b i ) ] m ∗ 1 , ( j = 1 , 2 , . . . , Q ) (6) T = [t_1,..,t_Q]_{m*Q},t_j = [t_{1j},...,t_{mj}]^T =\left[\begin{matrix}\sum_{i=1}^t\beta_{i1}g(w_ix_j + b_i)\\ \sum_{i=1}^t\beta_{i2}g(w_ix_j + b_i)\\ ...\\ \sum_{i=1}^t\beta_{im}g(w_ix_j + b_i) \end{matrix}\right]_{m*1},(j=1,2,...,Q)\tag{6} T=[t1,..,tQ]m∗Q,tj=[t1j,...,tmj]T= ∑i=1tβi1g(wixj+bi)∑i=1tβi2g(wixj+bi)...∑i=1tβimg(wixj+bi) m∗1,(j=1,2,...,Q)(6)
式(6)可表示为:
H β = T ’ (7) H\beta = T’ \tag{7} Hβ=T’(7)
其中, T’为矩阵 T 的转置; H 称为神经网络的隐含层输出矩阵 , 具体形式如下 :
H ( w 1 , . . . , w i , b 1 , . . . , b l , x 1 , . . . , x Q ) = [ g ( w 1 ∗ x 1 + b 1 ) g ( w 2 ∗ x 1 + b 2 ) . . . g ( w l ∗ x 1 + b l ) g ( w 1 ∗ x 2 + b 1 ) g ( w 2 ∗ x 2 + b 2 ) . . . g ( w l ∗ x 2 + b l ) . . . g ( w 1 ∗ x Q + b 1 ) g ( w 2 ∗ x Q + b 2 ) . . . g ( w l ∗ x Q + b l ) ] Q ∗ l H(w_1,...,w_i,b_1,...,b_l,x_1,...,x_Q) =\left[\begin{matrix} g(w_1*x_1 + b_1)&g(w_2*x_1 + b_2)&...&g(w_l*x_1 + b_l)\\ g(w_1*x_2 + b_1)&g(w_2*x_2 + b_2)&...&g(w_l*x_2 + b_l)\\ ...\\ g(w_1*x_Q + b_1)&g(w_2*x_Q + b_2)&...&g(w_l*x_Q + b_l) \end{matrix}\right]_{Q*l} H(w1,...,wi,b1,...,bl,x1,...,xQ)= g(w1∗x1+b1)g(w1∗x2+b1)...g(w1∗xQ+b1)g(w2∗x1+b2)g(w2∗x2+b2)g(w2∗xQ+b2).........g(wl∗x1+bl)g(wl∗x2+bl)g(wl∗xQ+bl) Q∗l
2.ELM学习算法
由前文分析可知,ELM在训练之前可以随机产生 w 和 b , 只需确定隐含层神经元个数及隐含层和神经元的激活函数(无限可微) , 即可计算出 β \beta β 。具体地, ELM 的学习算法主要有以下几个步骤:
(1)确定隐含层神经元个数,随机设定输入层与隐含层间的连接权值 w 和隐含层神经元的偏置 b ;
(2) 选择一个无限可微的函数作为隐含层神经元的激活函数,进而计算隐含层输出矩 阵 H ;
(3)计算输出层权值: β = H + T ′ \beta = H^+T' β=H+T′
值得一提的是,相关研究结果表明,在 ELM 中不仅许多非线性激活函数都可以使用(如 S 型函数、正弦函数和复合函数等),还可以使用不可微函数,甚至可以使用不连续的函数作为激 活函数。
3.回归问题数据处理
采用随机法产生训练集和测试集,其中训练集包含 1 900 个样 本,测试集包含 100 个样本。为了减少变量差异较大对模型性能的影响,在建立模型之前先对数据进行归一化。
4.基于灰狼算法优化的ELM
灰狼算法的具体原理参考博客:https://blog.csdn.net/u011835903/article/details/107716390
由前文可知,ELM的初始权值和阈值都是随机产生。每次产生的初始权值和阈值具有满目性。本文利用灰狼算法对初始权值和阈值进行优化。适应度函数设计为训练集的误差的MSE:
f i t n e s s = a r g m i n ( M S E p r i d e c t ) fitness = argmin(MSE_{pridect}) fitness=argmin(MSEpridect)
适应度函数选取训练后的MSE误差。MSE误差越小表明预测的数据与原始数据重合度越高。最终优化的输出为最佳初始权值和阈值。然后利用最佳初始权值阈值训练后的网络对测试数据集进行测试。
5.测试结果
灰狼算法相关参数如下:
%训练数据相关尺寸
R = size(Pn_train,1);
S = size(Tn_train,1);
N = 20;%隐含层个数
%% 定义灰狼优化参数
pop=20; %种群数量
Max_iteration=50; % 设定最大迭代次数
dim = N*R + N*S;%维度,即权值与阈值的个数
lb = [-1.*ones(1,N*R),zeros(1,N*S)];%下边界
ub = [ones(1,N*R),ones(1,N*S)];%上边界
将经过灰狼优化后的ELM与基础ELM进行对比。
预测结果如下图

基础ELM MSE误差:0.00014041
GWO-ELM MSE误差:3.9966e-10
从MSE看,灰狼-ELM明显优于基础ELM
6.参考文献
书籍《MATLAB神经网络43个案例分析》
7.Matlab代码
相关文章:

基于灰狼算法的极限学习机(ELM)回归预测-附代码
基于灰狼算法的极限学习机(ELM)回归预测 文章目录 基于灰狼算法的极限学习机(ELM)回归预测1.极限学习机原理概述2.ELM学习算法3.回归问题数据处理4.基于灰狼算法优化的ELM5.测试结果6.参考文献7.Matlab代码 摘要:本文利用灰狼算法对极限学习机进行优化,并…...

【五一创作】ERP实施-委外业务-委外采购业务
委外业务主要有两种业务形态:委外采购和工序外协,委外采购主要是在MM模块中实现,工序外协主要由PP模块实现,工序外协中的采购订单创建和采购收货由MM模块实现。 委外采购概念 委外采购,有些企业也称为带料委外或者分包…...

DAY 54 数据库基础
数据库的基本概念 数据(Data): 描述事务的符号记录包括数字、文字、图形、图像、声音、档案记录以”记录“形式按统一的格式进行存储 表: 将不同的记录组织在一起用来存储具体数据 数据库: 表的集合,…...
网络编程 总结二
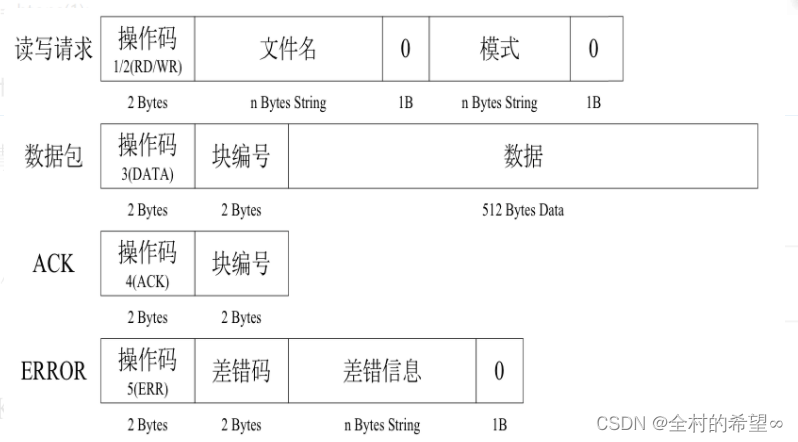
一、TCP TCP模型 1. TCP搭建相关函数: 套接字Socket 1)Socket函数: 2)bind 3)listen 4)accept 5)recv 注意: 1> TCP中的recv 可以替换成read; 2>TCP中的…...

消息称苹果Type-C口充电未设MFi限制,iOS17将更新Find My服务
根据国外科技媒体 iMore 报道,基于消息源 analyst941 透露的信息,苹果公司目前并未开发 MFi 限制。 根据推文信息内容,两款 iPhone 15 机型的最高充电功率为 20W,而 iPhone 15 Pro 机型的最高支持 27W 充电。 此前古尔曼表示苹…...

设计模式——工厂模式(简单工厂、工厂方法、抽象工厂)
是什么? 工厂模式的目的是将创建对象的具体过程隐藏起来,从而达到更高的灵活性 工厂模式分为:简单工厂模式、工厂方法模式、抽象工厂模式; 为什么? 在Java中,万物皆是对象,我们在使用的时候…...
《C语言技术体系》 学习路线总目录 + 思维导图
目录 前言 正文 思维导图 第1章 流程结构 1.1 初识C语言 1.2 流程结构 1.3 数据类型 1.4 运算符表达式 第2章 指针与数组 2.1 指针基本概念 2.2 一维数组 2.3 二维及多维数组 2.4 指针与数组 第3章 模块化重构 3.1 函数 3.2 typedef类型定义 3.3 enum枚举 3.…...

数字图像处理简答题
目录 1.人类视觉对颜色的主观感觉包括哪三类? 2. 图像成像的过程包括哪三步? 3.图像的采样和量化分别指什么? 4、取k8时,将下图用相应矩阵表示 5、简述当限定了数字图像的数据量时采样和量化参数的选择遵循哪两条原则&#x…...
【Java校招面试】基础知识(五)——GC
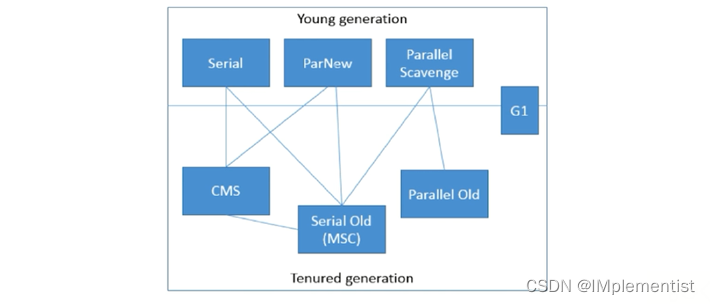
目录 前言一、基础概念二、垃圾回收算法三、垃圾收集器四、引用后记 前言 本篇主要介绍Java垃圾回收机制——GC的相关内容。 “基础知识”是本专栏的第一个部分,本篇博文是第五篇博文,如有需要,可: 点击这里,返回本专…...

使用CMake调用Makefile 项目
目录标题 基本示例Cmake传递lib给MakefileCmake传递参数给Makefile,比如make cleanWindows下使用Cmake调用Makefile 基本示例 如果项目是使用传统的Makefile构建的,并且您希望使用CMake调用这些Makefile,您可以使用CMake的add_custom_target…...
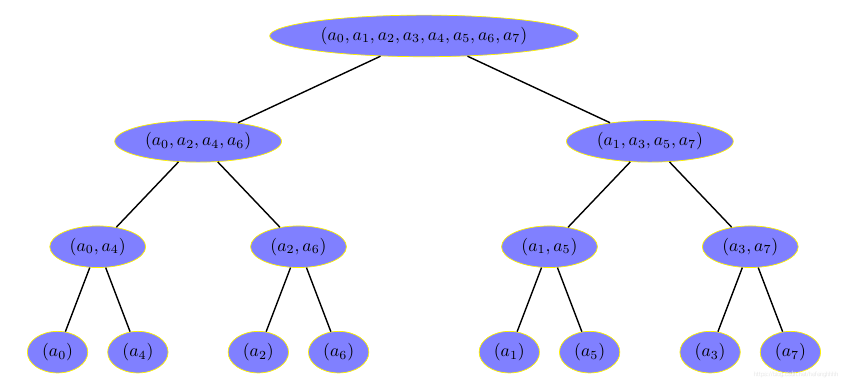
快速傅里叶变换FFT学习笔记
点值表示法 我们正常表示一个多项式的方式,形如 A ( x ) a 0 a 1 x a 2 x 2 . . . a n x n A(x)a_0a_1xa_2x^2...a_nx^n A(x)a0a1xa2x2...anxn,这是正常人容易看懂的,但是,我们还有一种表示法。 我们知道…...
如何下载安装驱动
1 打开浏览器 这里以Edge浏览器举例 第一步打开桌面上的Edge浏览器 如果您的桌面上没有 那么找到搜索栏 搜索Edge 然后打开 打开之后一般是这样 然后把我发送您的地址 驱动下载地址 https://t.lenovo.com.cn/yfeyfYyD (这个网址只是一个例子) 删除掉前…...

鸿蒙Hi3861学习四-Huawei LiteOS介绍
一、什么是LitesOS Huawei LiteOS是华为针对物联网领域推出的轻量级物联网操作系统,是华为物联网战略的重要组成部分,具备轻量级、低功耗、互联互通、组件丰富、快速开发等关键能力。基于物联网领域业务特征打造领域性技术栈,为开发者提供“一…...

Vue核心 收集表单数据 过滤器
1.14. 收集表单数据 收集表单数据: 若: ,则v-model收集的是value值,用户输入的就是value值。若: ,则v-model收集的是value值,且要给标签配置value值。若: 没有配置input的value属性,那么收集的就是checked(勾选 or 未…...
华为EC6108V9E/EC6108V9I_rk3228_安卓4.4.4_通刷_卡刷固件包
华为EC6108V9E/EC6108V9I_rk3228_安卓4.4.4_通刷_卡刷固件包-内有教程 特点: 1、适用于对应型号的电视盒子刷机; 2、开放原厂固件屏蔽的市场安装和u盘安装apk; 3、修改dns,三网通用; 4、大量精简内置的…...

数字化转型导师坚鹏:面向数字化转型的大数据顶层设计实践
面向数字化转型的大数据顶层设计实践 课程背景: 数字化背景下,很多企业存在以下问题: 不清楚大数据思维如何建立? 不清楚企业大数据分析方法? 不了解大数据应用成功案例? 课程特色: …...
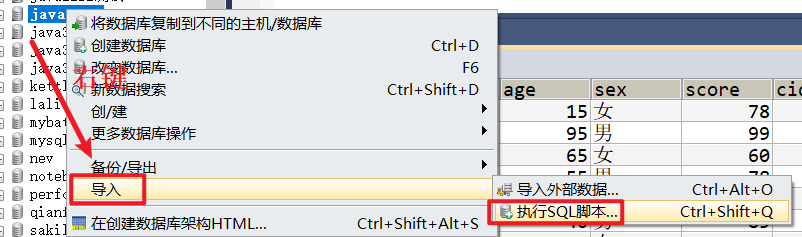
day27_mysql
今日内容 零、 复习昨日 一、单表查询 二、多表联查 零、 复习昨日 1 DDL,DML,DQL是啥 DDL 数据定义语言(库,表,列)DML 数据操作语言(表内数据的操作增删改)DQL 数据查询语言(表内数据的查询&am…...

QwtPlotCurve使用说明
QwtPlotCurve是Qwt库中用于绘制曲线的类,可以在QwtPlot上绘制各种类型的曲线,如折线、样条线、散点等。以下是QwtPlotCurve的一些常用函数和使用说明: setSamples(const QPolygonF &samples):设置曲线的数据点,参数…...
JS逆向 -- 某平台登录加密分析
一、打开网站,使用账号密码登录 账号:aiyou123.com 密码:123456 二、通过F12抓包,抓到如下数据,发现密码加密了 三、加密结果是32位,首先考虑是md5加密。 四、全局搜索pwd,点击右上角…...

一分钟快速实现Flask框架的蓝图和视图
一分钟快速实现Flask框架的蓝图和视图 Flask是一个轻量级的Web应用框架,非常适合快速开发小型的Web应用。Flask框架使用蓝图(Blueprint)和视图(View)的概念来组织应用程序的代码。在本文中,我们将介绍如何…...

stm32G473的flash模式是单bank还是双bank?
今天突然有人stm32G473的flash模式是单bank还是双bank?由于时间太久,我真忘记了。搜搜发现,还真有人和我一样。见下面的链接:https://shequ.stmicroelectronics.cn/forum.php?modviewthread&tid644563 根据STM32G4系列参考手…...

线程与协程
1. 线程与协程 1.1. “函数调用级别”的切换、上下文切换 1. 函数调用级别的切换 “函数调用级别的切换”是指:像函数调用/返回一样轻量地完成任务切换。 举例说明: 当你在程序中写一个函数调用: funcA() 然后 funcA 执行完后返回&…...

聊聊 Pulsar:Producer 源码解析
一、前言 Apache Pulsar 是一个企业级的开源分布式消息传递平台,以其高性能、可扩展性和存储计算分离架构在消息队列和流处理领域独树一帜。在 Pulsar 的核心架构中,Producer(生产者) 是连接客户端应用与消息队列的第一步。生产者…...

dedecms 织梦自定义表单留言增加ajax验证码功能
增加ajax功能模块,用户不点击提交按钮,只要输入框失去焦点,就会提前提示验证码是否正确。 一,模板上增加验证码 <input name"vdcode"id"vdcode" placeholder"请输入验证码" type"text&quo…...

MMaDA: Multimodal Large Diffusion Language Models
CODE : https://github.com/Gen-Verse/MMaDA Abstract 我们介绍了一种新型的多模态扩散基础模型MMaDA,它被设计用于在文本推理、多模态理解和文本到图像生成等不同领域实现卓越的性能。该方法的特点是三个关键创新:(i) MMaDA采用统一的扩散架构…...

Linux-07 ubuntu 的 chrome 启动不了
文章目录 问题原因解决步骤一、卸载旧版chrome二、重新安装chorme三、启动不了,报错如下四、启动不了,解决如下 总结 问题原因 在应用中可以看到chrome,但是打不开(说明:原来的ubuntu系统出问题了,这个是备用的硬盘&a…...

Mysql8 忘记密码重置,以及问题解决
1.使用免密登录 找到配置MySQL文件,我的文件路径是/etc/mysql/my.cnf,有的人的是/etc/mysql/mysql.cnf 在里最后加入 skip-grant-tables重启MySQL服务 service mysql restartShutting down MySQL… SUCCESS! Starting MySQL… SUCCESS! 重启成功 2.登…...

【p2p、分布式,区块链笔记 MESH】Bluetooth蓝牙通信 BLE Mesh协议的拓扑结构 定向转发机制
目录 节点的功能承载层(GATT/Adv)局限性: 拓扑关系定向转发机制定向转发意义 CG 节点的功能 节点的功能由节点支持的特性和功能决定。所有节点都能够发送和接收网格消息。节点还可以选择支持一个或多个附加功能,如 Configuration …...

【Linux手册】探秘系统世界:从用户交互到硬件底层的全链路工作之旅
目录 前言 操作系统与驱动程序 是什么,为什么 怎么做 system call 用户操作接口 总结 前言 日常生活中,我们在使用电子设备时,我们所输入执行的每一条指令最终大多都会作用到硬件上,比如下载一款软件最终会下载到硬盘上&am…...

一些实用的chrome扩展0x01
简介 浏览器扩展程序有助于自动化任务、查找隐藏的漏洞、隐藏自身痕迹。以下列出了一些必备扩展程序,无论是测试应用程序、搜寻漏洞还是收集情报,它们都能提升工作流程。 FoxyProxy 代理管理工具,此扩展简化了使用代理(如 Burp…...
