动态规划算法——40道leetcode实例入门到熟练
目录
- t0.解题五部曲
- 1.基础入门题目
- 1.509. 斐波那契数
- 2.70. 爬楼梯
- 3.746. 使用最小花费爬楼梯
- 4.62. 不同路径
- 5.63. 不同路径 II
- 6.343. 整数拆分
- 7.96. 不同的二叉搜索树
- 2.背包问题
- 1.01背包(二维数组实现)
- 2.01背包(滚动数组实现)
- 1.416. 分割等和子集
- 2.1049. 最后一块石头的重量 II
- *3.494. 目标和
- 4.474. 一和零
- 2.完全背包
- 1.518. 零钱兑换 II
- 2.377. 组合总和 Ⅳ
- 3.322. 零钱兑换
- 4.279. 完全平方数
- *5.139. 单词拆分
- 3.打家劫舍
- 1.198. 打家劫舍
- 2.213. 打家劫舍 II
- 3.337. 打家劫舍 III
- 4.股票问题
- 1.121. 买卖股票的最佳时机
- 2.122. 买卖股票的最佳时机 II
- 3.123. 买卖股票的最佳时机 III
- 4.188. 买卖股票的最佳时机 IV
- 5.309. 最佳买卖股票时机含冷冻期
- 6.714. 买卖股票的最佳时机含手续费
- 5.子序列问题
- 1.子序列(不连续)
- 1.300. 最长递增子序列
- 2.1143. 最长公共子序列
- 3.1035. 不相交的线
- 2.子序列(连续)
- 1.674. 最长连续递增序列
- *2.718. 最长重复子数组
- 3.53. 最大子数组和
- 3.编辑距离
- 1.392. 判断子序列
- 2.115. 不同的子序列
- 3.583. 两个字符串的删除操作
- 4.72. 编辑距离
- 4.回文
- 1.647. 回文子串
- 2.516. 最长回文子序列
t0.解题五部曲
1. 确定dp数组(dp table)以及下标的含义
2. 确定递推公式
3. dp数组如何初始化
4. 确定遍历顺序
5. 举例推导dp数组
1.基础入门题目
1.509. 斐波那契数
链接: 509. 斐波那契数
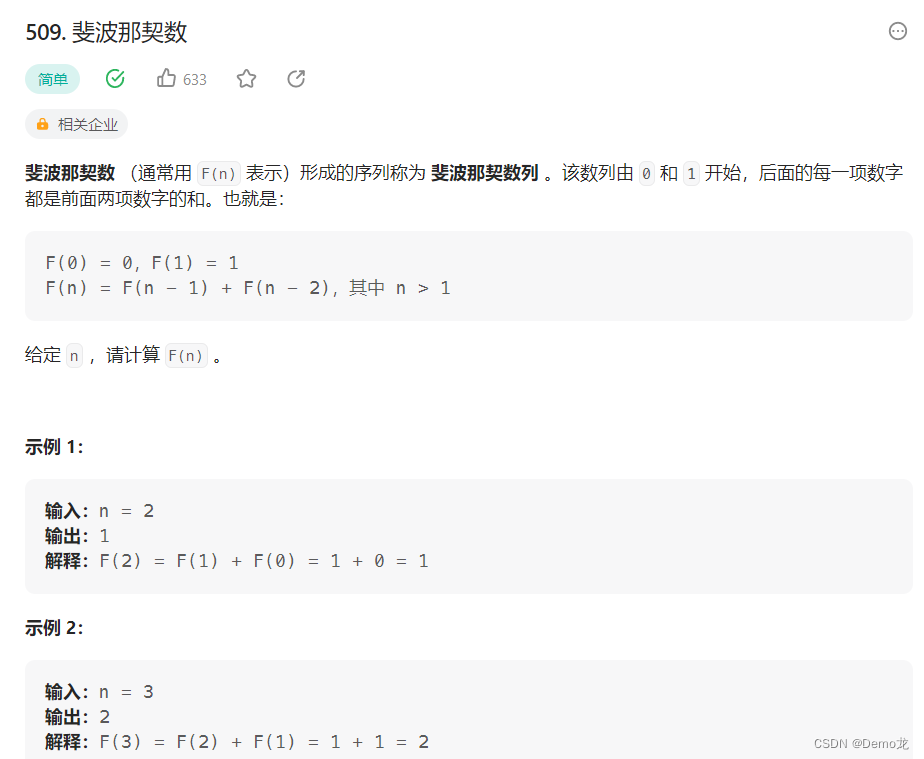
class Solution {public int fib(int n) {if(n<=1){return n;}int arr[]=new int[n+1];arr[0]=1;arr[1]=1;for(int i=2;i<=n;i++){arr[i]=arr[i-2]+arr[i-1];}return arr[n-1];}
}
class Solution {public int fib(int n) {if(n<=1){return n;}int arr0=0;int arr1=1;for(int i=2;i<=n;i++){int sum=arr0+arr1;arr0=arr1;arr1=sum;}return arr1;}
}
2.70. 爬楼梯
链接: 70. 爬楼梯
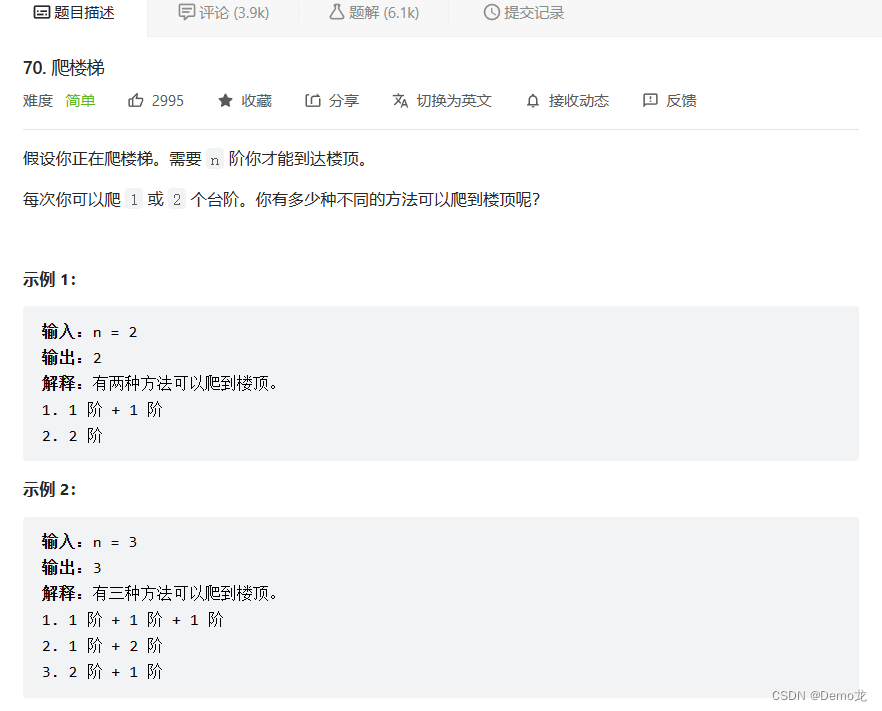
class Solution {public int climbStairs(int n) {if(n<=2){return n;}int dp[]=new int[n+1];dp[1]=1;dp[2]=2;for(int i=3;i<=n;i++){dp[i]=dp[i-1]+dp[i-2];}return dp[n];}
}
3.746. 使用最小花费爬楼梯
链接: 746. 使用最小花费爬楼梯
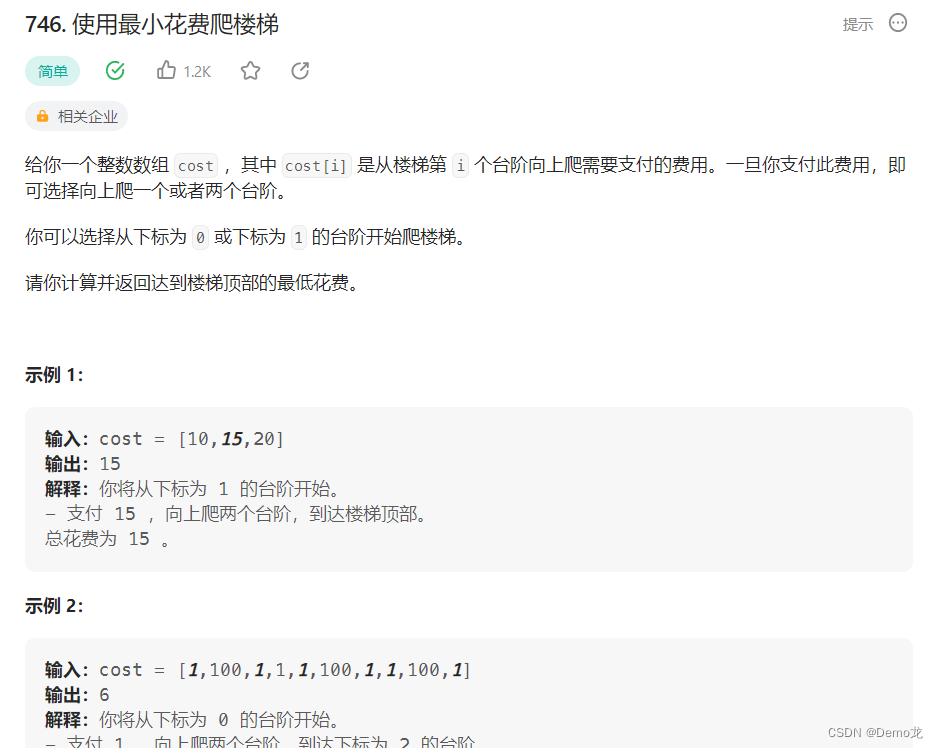
class Solution {public int minCostClimbingStairs(int[] cost) {int n=cost.length;int dp[]=new int [n+1];dp[0]=0;dp[1]=0;for(int i=2;i<=n;i++){dp[i]=Math.min((dp[i-1]+cost[i-1]),(dp[i-2]+cost[i-2]));}return dp[n];}
}
4.62. 不同路径
链接: 62. 不同路径
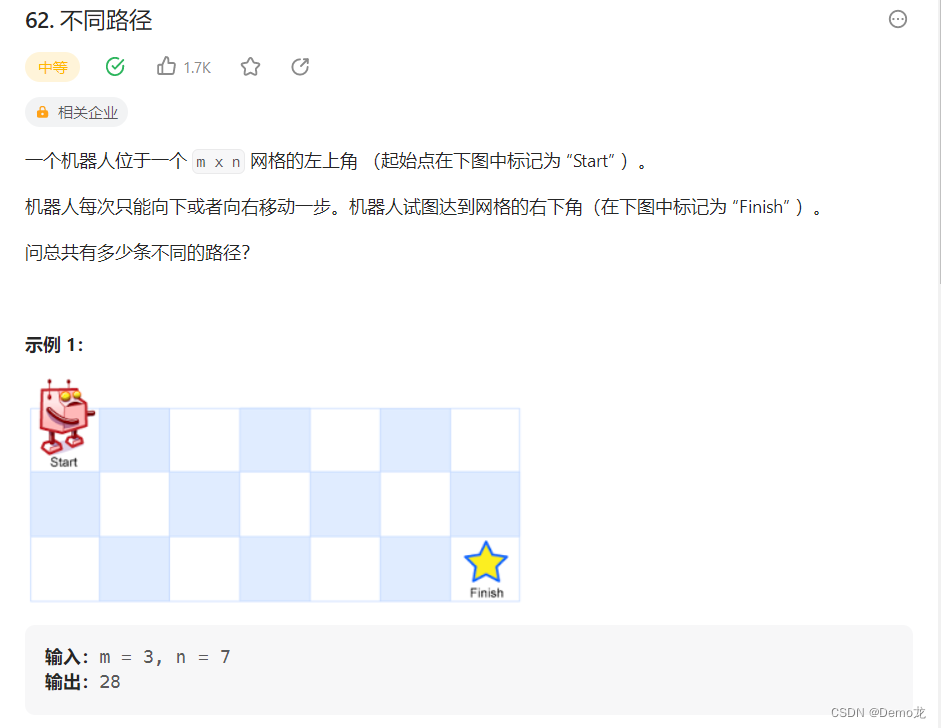
class Solution {public int uniquePaths(int m, int n) {int dp[][]=new int[m][n];for(int i=0;i<m;i++){dp[i][0]=1;}for(int i=0;i<n;i++){dp[0][i]=1;}for(int i=1;i<m;i++){for(int j=1;j<n;j++){dp[i][j]=dp[i-1][j]+dp[i][j-1];}}return dp[m-1][n-1];}
}
5.63. 不同路径 II

链接: 63. 不同路径 II
class Solution {public int uniquePathsWithObstacles(int[][] obstacleGrid) {int m=obstacleGrid.length;int n=obstacleGrid[0].length;if(obstacleGrid[m-1][n-1]==1||obstacleGrid[0][0]==1){return 0;//当start位置和finish位置有障碍时直接返回0}int dp[][]=new int[m][n];//从start每一个坐标点有多少条不同的路径for(int i=0;i<m&&obstacleGrid[i][0]==0;i++){dp[i][0]=1;//满足条件初始化第一列,若有障碍后面的dp都为0}for(int i=0;i<n&&obstacleGrid[0][i]==0;i++){dp[0][i]=1;//满足条件初始化第一行,若有障碍后面的dp都为0}for(int i=1;i<m;i++){for(int j=1;j<n;j++){if(obstacleGrid[i][j]==0){dp[i][j]=dp[i-1][j]+dp[i][j-1];}}}return dp[m-1][n-1];}
}6.343. 整数拆分
链接: 343. 整数拆分
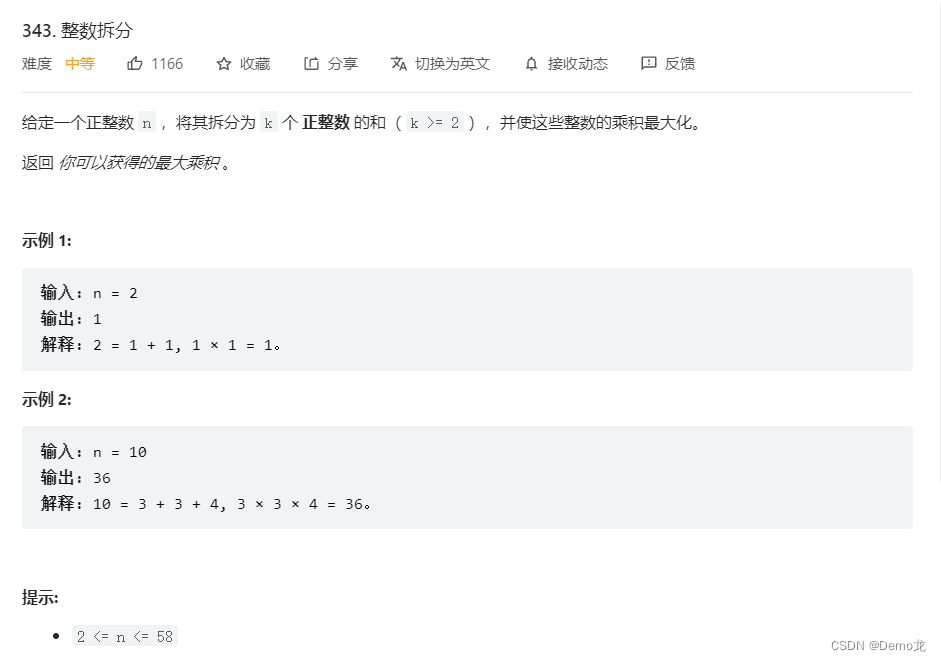
class Solution {public int integerBreak(int n) {int dp[]=new int[n+1];dp[2]=1;for(int i=3;i<=n;i++){for(int j=1;j<=i/2;j++){dp[i]=Math.max(dp[i],Math.max(j*dp[i-j],j*(i-j)));}}return dp[n];}
}
7.96. 不同的二叉搜索树
链接: 96. 不同的二叉搜索树
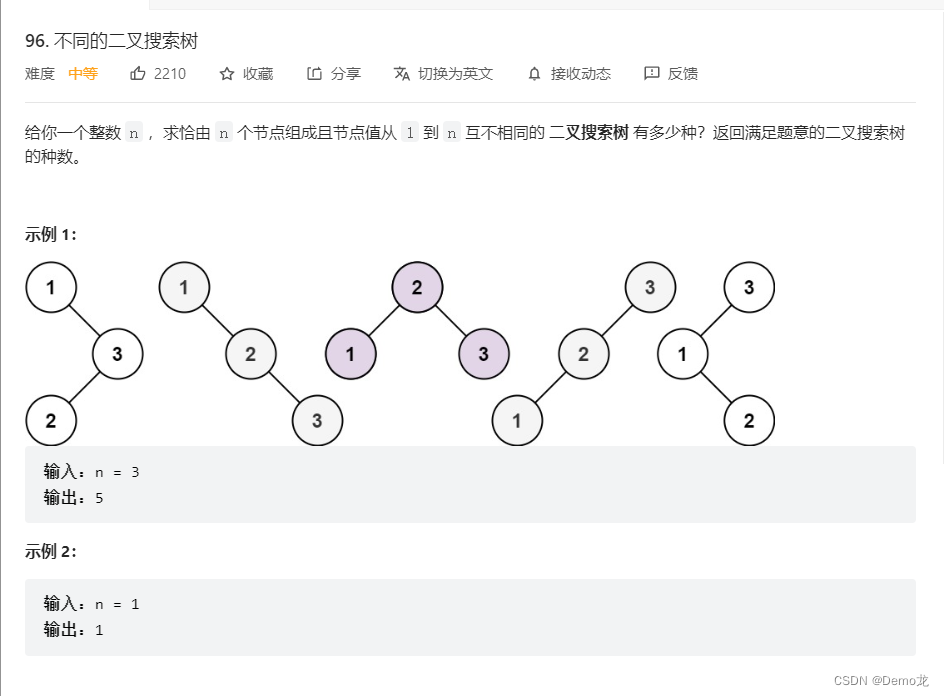
class Solution {public int numTrees(int n) {int dp[]=new int[n+1];dp[0]=1;for(int i=1;i<=n;i++){for(int j=1;j<=i;j++){dp[i]+=dp[i-j]*dp[j-1];}}return dp[n];}
}
2.背包问题
1.01背包(二维数组实现)
1.dp[i][j]数组含义:dp[i][j] 表⽰从下标为[0-i]的物品⾥任意取,放进容量为j的背包,价值总和最⼤是多少。
2.递推方程:dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);
01背包问题Java代码
public class Knapsack_problem01 {//01背包问题public static void main(String[] args) {System.out.println("背包最大价值"+knapsack());}//01背包//dp[i][j]数组含义:dp[i][j] 表⽰从下标为[0-i]的物品⾥任意取,//放进容量为j的背包,价值总和最⼤是多少。public static int knapsack(){int wight[]={1,3,4};int value[]={15,20,30};int bagW=4;int [][]dp=new int[wight.length][bagW+1];for (int i = bagW; i >= wight[0]; i--) {//初始化dpdp[0][i]=value[0];}//打印初始化后的dp数组System.out.println("=====初始化后的dp=====");printDP(dp);// for(int i=1;i<=bagW;i++){//先遍历背包容量
// for (int j = 1; j < wight.length; j++){//遍历物品,wight数组的大小就是物品个数
// if(i-wight[j]>=0)
// dp[j][i]=Math.max(dp[j-1][i],(dp[j-1][i-wight[j]]+value[j]));
// }
// }for(int i=1;i<wight.length;i++){//先遍历物品,wight数组的大小就是物品个数for (int j = 1; j <= bagW; j++){//遍历背包if(j-wight[i]>=0)dp[i][j]=Math.max(dp[i-1][j],(dp[i-1][j-wight[i]]+value[i]));}}//打印dp数组System.out.println("=====递推后的·dp=====");printDP(dp);return dp[wight.length-1][bagW];}//打印dp数组public static void printDP(int [][]dp){for (int i = 0; i < dp.length; i++) {for (int j = 0; j < dp[0].length; j++) {System.out.print(dp[i][j]+" ");}System.out.println();}}}
2.01背包(滚动数组实现)
- 在使⽤⼆维数组的时候,递推公式:dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] +value[i]);
- 其实可以发现如果把dp[i - 1]那⼀层拷贝到dp[i]上,表达式完全可以是:dp[i][j] = max(dp[i][j], dp[i][j - weight[i]] + value[i]); 于其把dp[i -1]这⼀层拷贝到dp[i]上,不如只⽤⼀个⼀维数组了,只⽤dp[j](⼀维数组,也 可以理解是⼀个滚动数组)。
1. 确定dp数组的定义
在⼀维dp数组中,dp[j]表⽰:容量为j的背包,所背的物品价值可以最⼤为dp[j]。
2.递推公式
dp[j] = max(dp[j], dp[j - weight[i]] + value[i])
java代码
//01背包(一维滚动数组实现)//在⼀维dp数组中,dp[j]表⽰:容量为j的背包,所背的物品价值可以最⼤为dp[j]。public static int knapsack02(){int weight[]={1,3,4};int value[]={15,20,30};int bagW=4;int []dp=new int[bagW+1];//默认初始化为0for(int i = 0; i < weight.length; i++) { // 遍历物品for(int j = bagW; j >= weight[i]; j--) { // 遍历背包容量dp[j] = Math.max(dp[j], dp[j-weight[i]]+value[i]);}}return dp[bagW];}

1.416. 分割等和子集
链接: 416. 分割等和子集
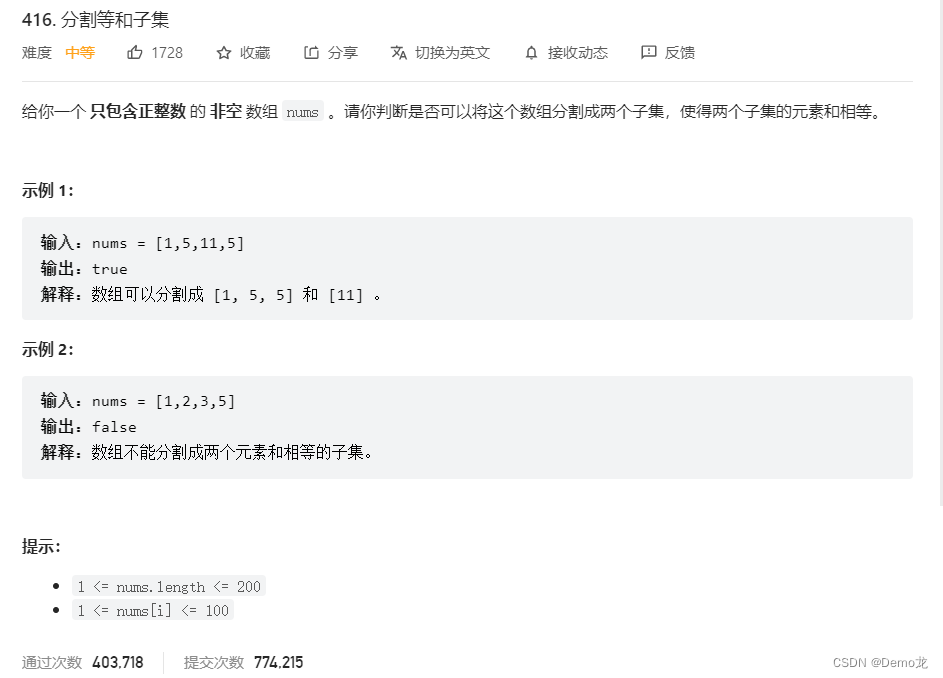
class Solution {public boolean canPartition(int[] nums) {int target=0;for(int i=0;i<nums.length;i++){target+=nums[i];}if(target%2!=0){return false;}target=target/2;int dp[]=new int[target+1];//默认初始化为0for(int i=0;i<nums.length;i++){//先遍历物品for(int j=target;j>=nums[i];j--){//倒序遍历背包,确保每个物品只能进入一次dp[j]=Math.max(dp[j],dp[j-nums[i]]+nums[i]);}}if(dp[target]==target){return true;}return false;}
}
2.1049. 最后一块石头的重量 II
链接: 1049. 最后一块石头的重量 II

class Solution {public int lastStoneWeightII(int[] stones) {int sum=0;for(int i=0;i<stones.length;i++){sum+=stones[i];}int target=sum/2;//将stones数组一分为二,找到重量最接近target的dp数组int dp[]=new int[target+1];//默认初始化为0for(int i=0;i<stones.length;i++){//先遍历石头for(int j=target;j>=stones[i];j--){//再逆序遍历背包dp[j]=Math.max(dp[j],dp[j-stones[i]]+stones[i]);}}int min_Weight=(sum-dp[target])-dp[target];//一分为二的石头相减得到最小重量return min_Weight;}
}
*3.494. 目标和
链接: 494. 目标和
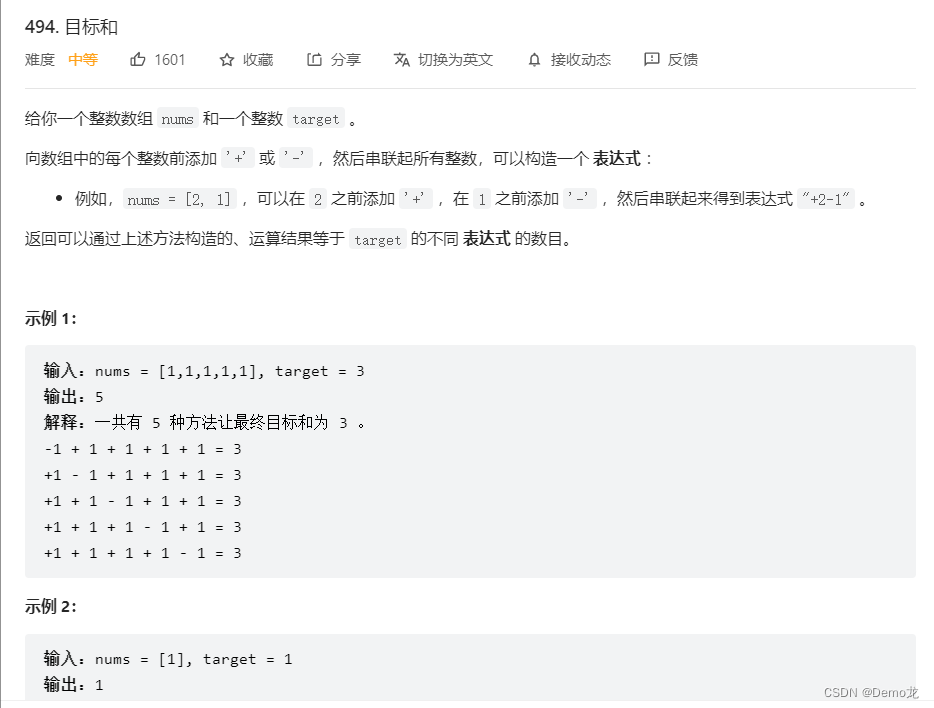

class Solution {public int findTargetSumWays(int[] nums, int target) {int sum = 0;for (int i = 0; i < nums.length; i++) sum += nums[i];if(Math.abs(target)>sum){//如果target的绝对值大于sum,此时没有方案return 0;}if ((target + sum) % 2 == 1) return 0; // 此时没有⽅案int bagSize=(sum+target)/2;int dp[]=new int[bagSize+1];dp[0]=1;for(int i=0;i<nums.length;i++){for(int j=bagSize;j>=nums[i];j--){dp[j]+=dp[j-nums[i]];}}return dp[bagSize];}
}
4.474. 一和零
链接: 474. 一和零

class Solution {public int findMaxForm(String[] strs, int m, int n) {int dp[][]=new int[m+1][n+1];//默认初始化为0;for(String str:strs){int num1=0;int num0=0;for(char c:str.toCharArray()){if(c=='1'){num1++;}else{num0++;}}for(int i=m;i>=num0;i--){for(int j=n;j>=num1;j--){dp[i][j]=Math.max(dp[i][j],dp[i-num0][j-num1]+1);}}}return dp[m][n];}
}
2.完全背包
public class CompleteBackpack {//完全背包问题public static void main(String[] args) {System.out.println(test_CompletePack());}// 先遍历物品,在遍历背包public static int test_CompletePack() {int []weight = {1, 3, 4};int []value = {15, 20, 30};int bagWeight = 4;int dp[]=new int[bagWeight + 1];for(int i = 0; i < weight.length; i++) { // 遍历物品for(int j = weight[i]; j <= bagWeight; j++) { // 遍历背包容量//正序遍历,每个物品可以选多次dp[j] = Math.max(dp[j], dp[j - weight[i]] + value[i]);}}return dp[bagWeight];}
}1.518. 零钱兑换 II
链接: 518. 零钱兑换 II
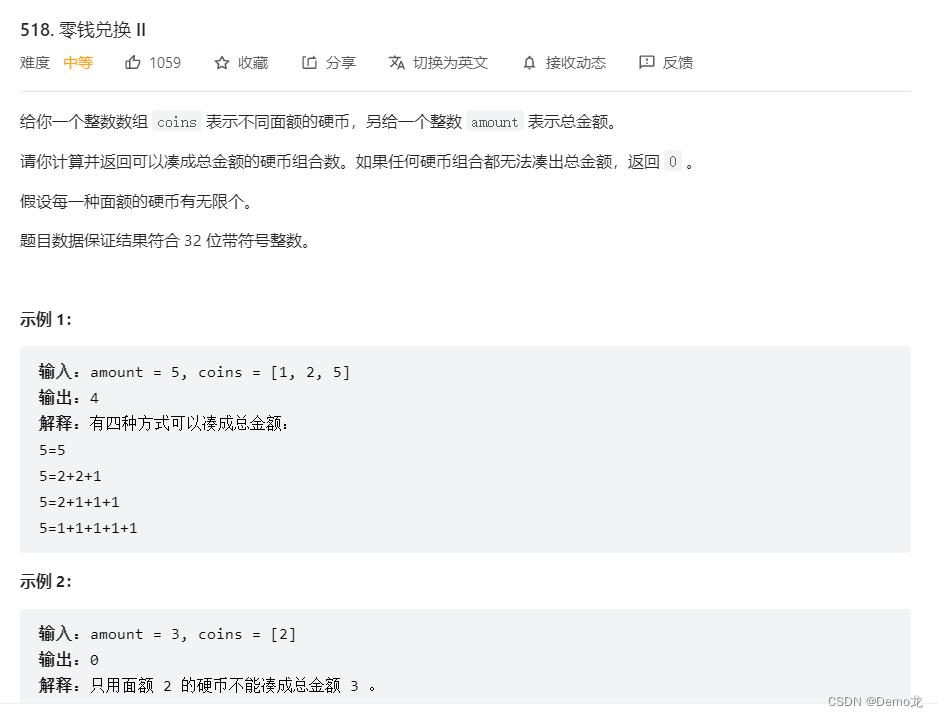
class Solution {public int change(int amount, int[] coins) {int n=coins.length;int dp[]=new int[amount+1];//默认初始化为0dp[0]=1;//初始化不放入物品的方式有一种for(int i=0;i<n;i++){for(int j=coins[i];j<=amount;j++){dp[j]+=dp[j-coins[i]];}}return dp[amount];}
}
2.377. 组合总和 Ⅳ
链接: 377. 组合总和 Ⅳ
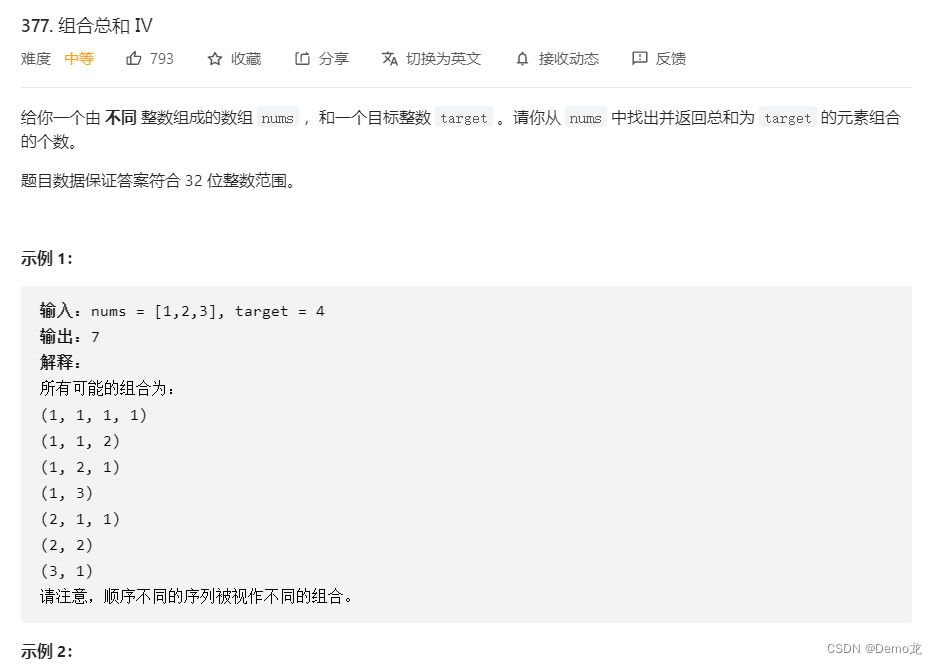
class Solution {public int combinationSum4(int[] nums, int target) {int dp[]=new int[target+1];dp[0]=1;for(int i=0;i<=target;i++){for(int j=0;j<nums.length;j++){if (i >= nums[j] )dp[i]+=dp[i-nums[j]];}}return dp[target];}
}
3.322. 零钱兑换
链接: 322. 零钱兑换
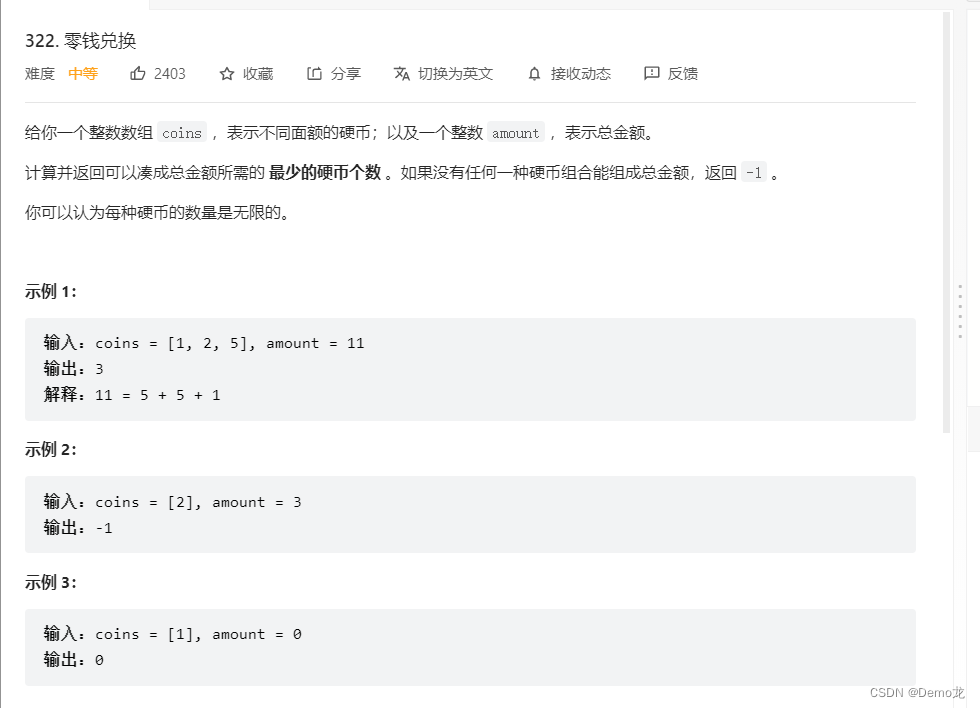
class Solution {public int coinChange(int[] coins, int amount) {int n=coins.length;int dp[]=new int[amount+1];//默认初始化为0dp[0]=0;//先凑⾜总⾦额为0所需钱币的个数⼀定是0for(int i=1;i<=amount;i++){dp[i]=Integer.MAX_VALUE;}for(int i=0;i<n;i++){for(int j=coins[i];j<=amount;j++){if(dp[j-coins[i]]!=Integer.MAX_VALUE)dp[j]=Math.min(dp[j-coins[i]]+1,dp[j]);}}if(dp[amount]==Integer.MAX_VALUE)return -1;return dp[amount];}
}
4.279. 完全平方数
链接: 279. 完全平方数
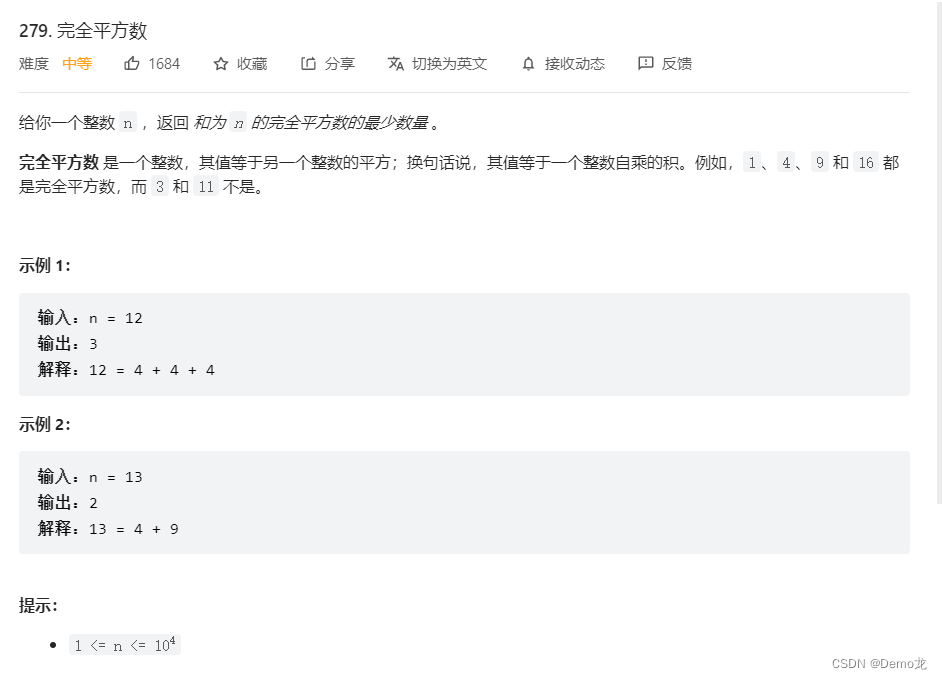
class Solution {public int numSquares(int n) {int dp[]=new int[n+1];dp[0]=0;for(int i=1;i<=n;i++){dp[i]=Integer.MAX_VALUE;}for(int i=0;i*i<=n;i++){for(int j=i*i;j<=n;j++){if(dp[j-i*i]!=Integer.MAX_VALUE)dp[j]=Math.min(dp[j-i*i]+1,dp[j]);}}return dp[n];}
}
*5.139. 单词拆分
链接: 139. 单词拆分
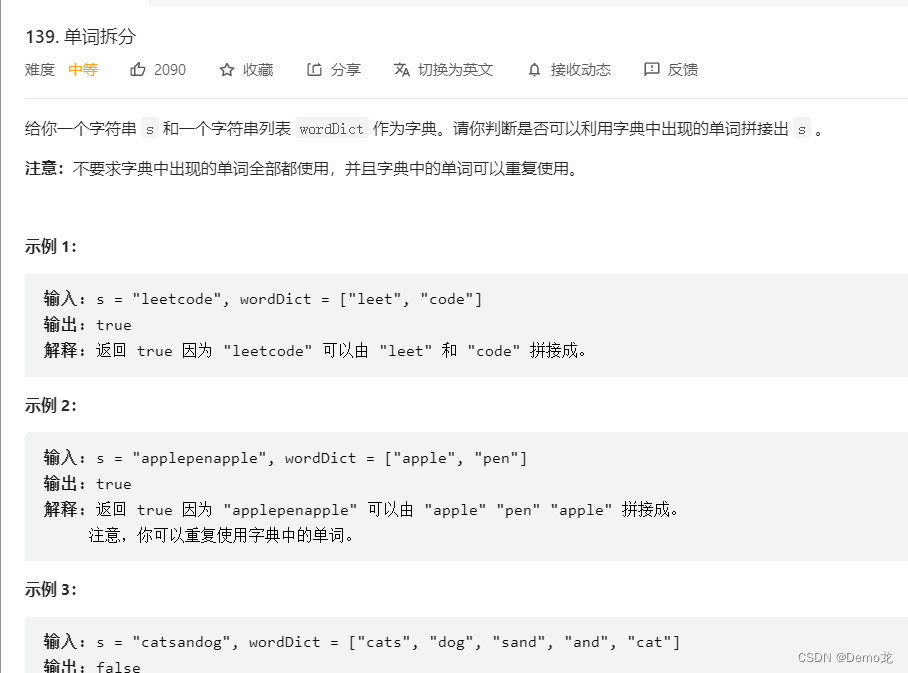
class Solution {public boolean wordBreak(String s, List<String> wordDict) {int n=s.length();boolean[] dp = new boolean[n + 1];dp[0]=true;for(int i=0;i<=n;i++){for(int j=0;j<i;j++){if(dp[j]&&wordDict.contains(s.substring(j,i))){dp[i]=true;break;}}}return dp[n];}
}
3.打家劫舍
1.198. 打家劫舍
链接: 198. 打家劫舍
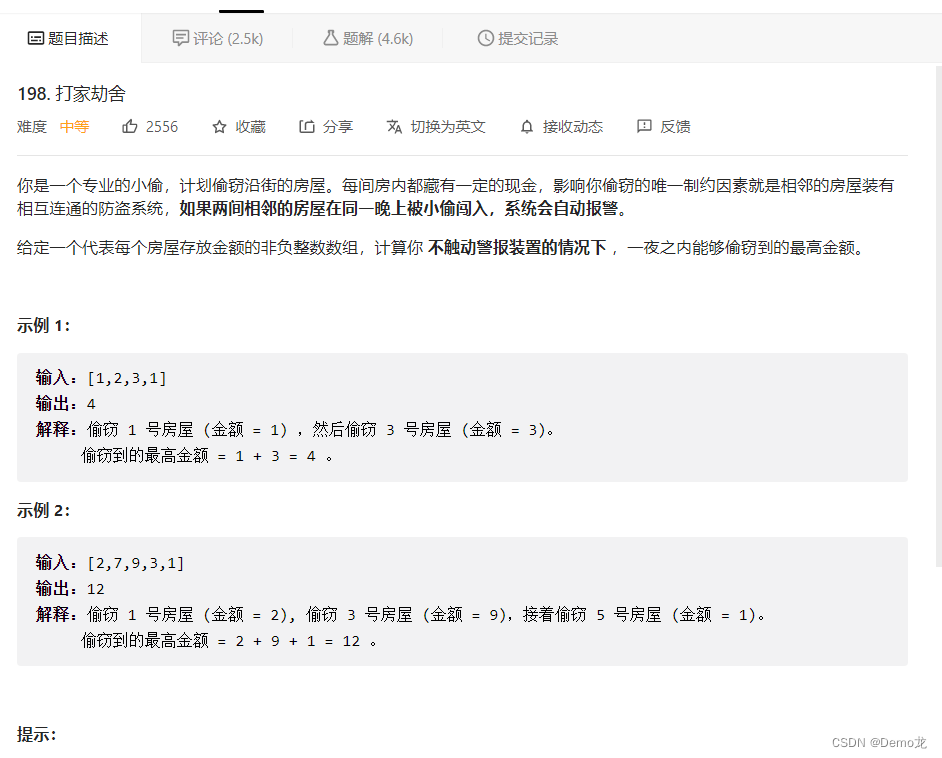
class Solution {public int rob(int[] nums) {int n=nums.length;if(n<=1){return nums[0];}int dp[]=new int[n];//默认初始化为0dp[0]=nums[0];dp[1]=Math.max(nums[0],nums[1]);for(int i=2;i<n;i++){dp[i]=Math.max((nums[i]+dp[i-2]),dp[i-1]);}return dp[n-1];}
}
2.213. 打家劫舍 II
链接: 213. 打家劫舍 II
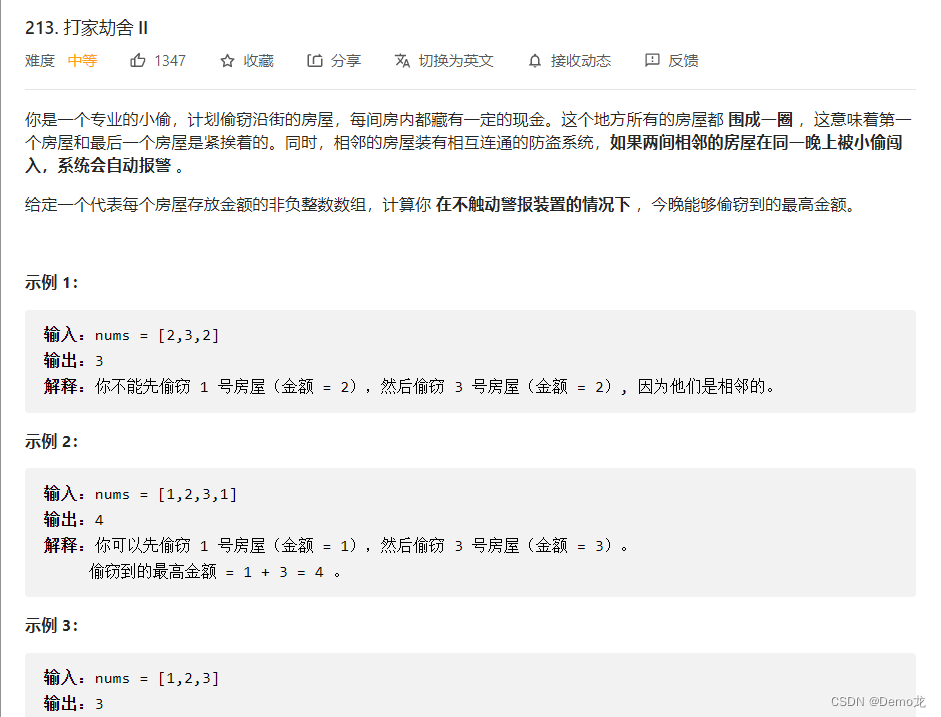
class Solution {public int rob(int[] nums) {int n=nums.length;if(n<=1){return nums[0];}else if(n==2){return Math.max(nums[0],nums[1]);}return Math.max(fun(nums,0,n-1),fun(nums,1,n));}public int fun(int[] nums,int i,int n) {int dp[]=new int[n];//默认初始化为0dp[i]=nums[i];dp[i+1]=Math.max(nums[i],nums[i+1]);for(int j=i+2;j<n;j++){dp[j]=Math.max((nums[j]+dp[j-2]),dp[j-1]);}return dp[n-1];}
}
3.337. 打家劫舍 III
链接: 337. 打家劫舍 III
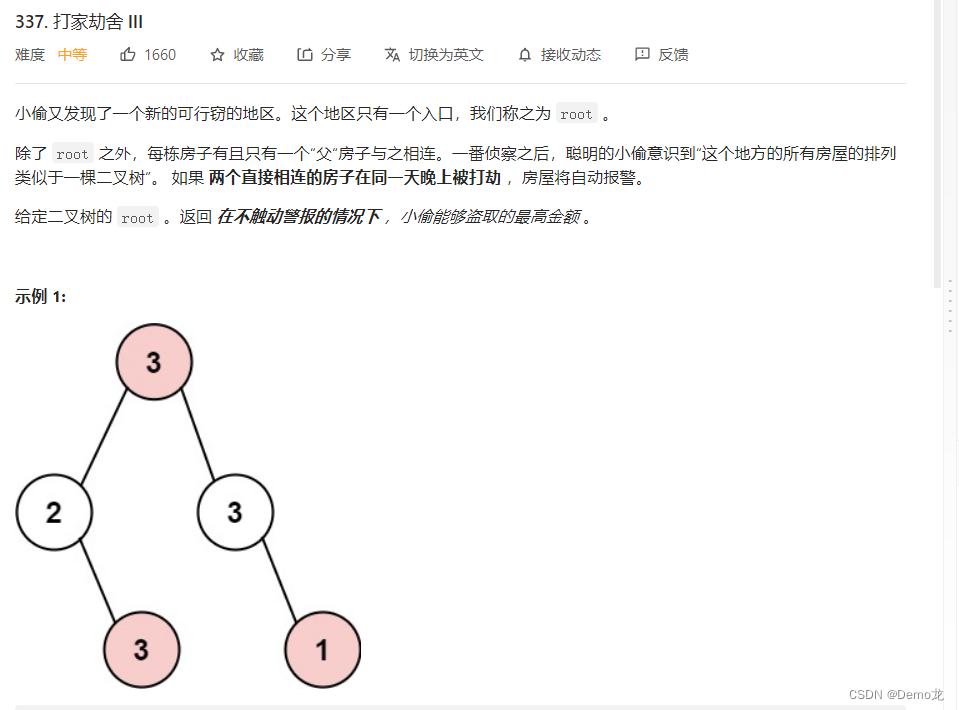
/*** Definition for a binary tree node.* public class TreeNode {* int val;* TreeNode left;* TreeNode right;* TreeNode() {}* TreeNode(int val) { this.val = val; }* TreeNode(int val, TreeNode left, TreeNode right) {* this.val = val;* this.left = left;* this.right = right;* }* }*/
class Solution {public int rob(TreeNode root) {int result[] = robTree(root);return Math.max(result[0], result[1]);}// ⻓度为2的数组,0:不偷,1:偷int[] robTree(TreeNode cur) {if (cur == null) return new int[]{0, 0};int left[] = robTree(cur.left);int right[] = robTree(cur.right);// 偷curint val1 = cur.val + left[0] + right[0];// 不偷curint val2 = Math.max(left[0], left[1]) + Math.max(right[0], right[1]);return new int[]{val2, val1};}
}4.股票问题
1.121. 买卖股票的最佳时机
链接: 121. 买卖股票的最佳时机
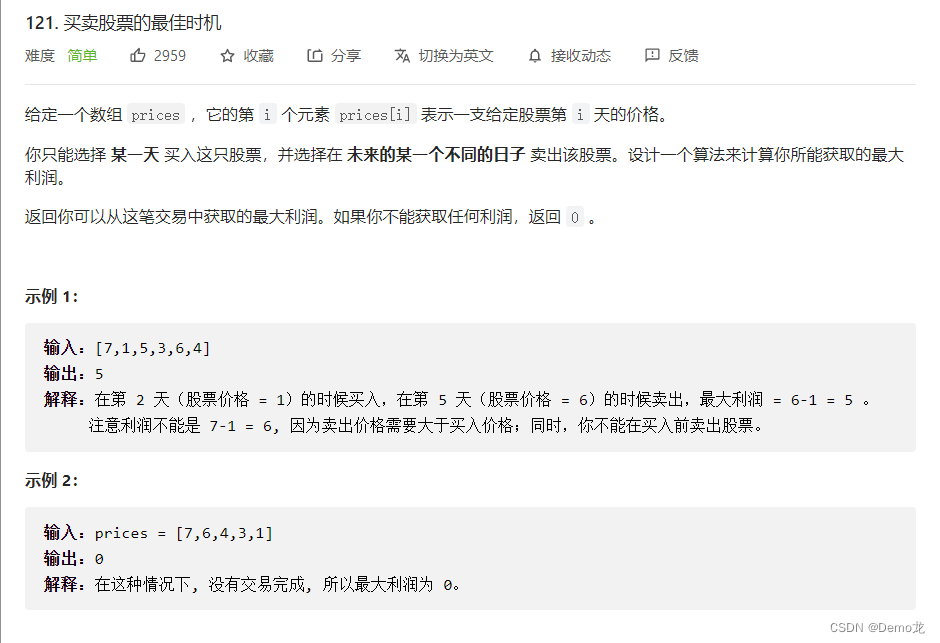
class Solution {public int maxProfit(int[] prices) {int n=prices.length;if(n==0){return 0;}int [][]dp=new int[n][2];dp[0][0]=-prices[0];dp[0][1]=0;for(int i=1;i<n;i++){dp[i][0]=Math.max(dp[i-1][0],-prices[i]);dp[i][1]=Math.max(dp[i-1][1],prices[i]+dp[i-1][0]);}return dp[n-1][1];}
}
2.122. 买卖股票的最佳时机 II
链接: 122. 买卖股票的最佳时机 II
class Solution {public int maxProfit(int[] prices) {int n=prices.length;if(n==0){return 0;}int [][]dp=new int[n][2];dp[0][0]=-prices[0];dp[0][1]=0;for(int i=1;i<n;i++){dp[i][0]=Math.max(dp[i-1][0],dp[i-1][1]-prices[i]);//和1唯一不同dp[i][1]=Math.max(dp[i-1][1],prices[i]+dp[i-1][0]);}return dp[n-1][1];}
}
3.123. 买卖股票的最佳时机 III
链接: 123. 买卖股票的最佳时机 III
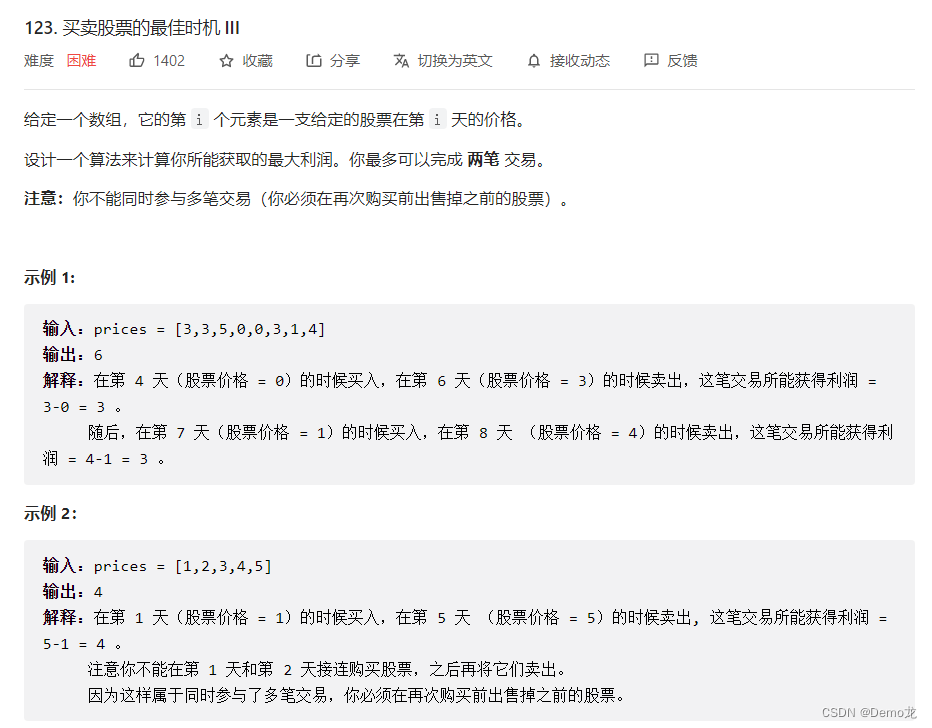
class Solution {public int maxProfit(int[] prices) {int n=prices.length;if(n==0){return 0;}int [][]dp=new int[n][4];dp[0][0]=-prices[0];//第一次持有dp[0][1]=0;//第一次不持有dp[0][2]=-prices[0];//第二次持有dp[0][3]=0;//第二次不持有for(int i=1;i<n;i++){dp[i][0]=Math.max(dp[i-1][0],-prices[i]);dp[i][1]=Math.max(dp[i-1][1],dp[i-1][0]+prices[i]);dp[i][2]=Math.max(dp[i-1][2],dp[i-1][1]-prices[i]);dp[i][3]=Math.max(dp[i-1][3],dp[i-1][2]+prices[i]);}return dp[n-1][3];}
}
4.188. 买卖股票的最佳时机 IV
链接: 188. 买卖股票的最佳时机 IV

class Solution {public int maxProfit(int k, int[] prices) {int n=prices.length;if(n==0)return 0;int [][]dp=new int[n][2*k+1];//初始化默认为0for(int j=1;j<2*k;j+=2){dp[0][j]=-prices[0];//第j次持有}for(int i=1;i<n;i++){for(int j=0;j<2*k;j+=2){dp[i][j+1]=Math.max(dp[i-1][j+1],dp[i-1][j]-prices[i]);dp[i][j+2]=Math.max(dp[i-1][j+2],dp[i-1][j+1]+prices[i]);}}return dp[n-1][2*k];}
}5.309. 最佳买卖股票时机含冷冻期
链接: 309. 最佳买卖股票时机含冷冻期
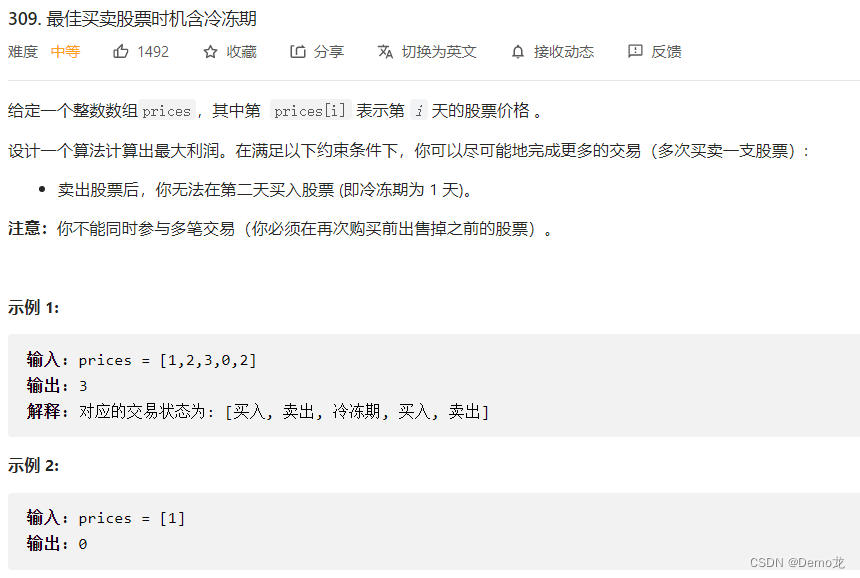
class Solution {public int maxProfit(int[] prices) {int n=prices.length;if(n==0){return 0;}int [][]dp=new int[n][4];dp[0][0]=-prices[0];//持股dp[0][1]=0;//保持卖出股dp[0][2]=0;//卖出股dp[0][3]=0;//冷冻期for(int i=1;i<n;i++){dp[i][0]=Math.max(dp[i-1][0],Math.max(dp[i-1][1],dp[i-1][3])-prices[i]);dp[i][1]=Math.max(dp[i-1][1],dp[i-1][3]);dp[i][2]=dp[i-1][0]+prices[i];dp[i][3]=dp[i-1][2];}return Math.max(dp[n - 1][3],Math.max(dp[n - 1][1], dp[n - 1][2]));}
}
6.714. 买卖股票的最佳时机含手续费
链接: 714. 买卖股票的最佳时机含手续费

class Solution {public int maxProfit(int[] prices, int fee) {int n=prices.length;if(n==0){return 0;}int [][]dp=new int[n][2];dp[0][0]=-prices[0];dp[0][1]=0;for(int i=1;i<n;i++){dp[i][0]=Math.max(dp[i-1][0],dp[i-1][1]-prices[i]);dp[i][1]=Math.max(dp[i-1][1],prices[i]+dp[i-1][0]-fee);}return dp[n-1][1];}
}
5.子序列问题
1.子序列(不连续)
1.300. 最长递增子序列
链接: 300. 最长递增子序列

class Solution {public int lengthOfLIS(int[] nums) {int n=nums.length;if(n<=1){return n;}int dp[]=new int[n];for(int i=0;i<n;i++){dp[i]=1;}int result=0;for(int i=1;i<n;i++){for(int j=0;j<i;j++){if(nums[i]>nums[j]){dp[i]=Math.max(dp[j]+1,dp[i]);}}result=Math.max(result,dp[i]);}return result;}
}
2.1143. 最长公共子序列
链接: 1143. 最长公共子序列

class Solution {public int longestCommonSubsequence(String text1, String text2) {char []nums1=text1.toCharArray();char []nums2=text2.toCharArray();int n1=nums1.length;int n2=nums2.length;int dp[][]=new int[n1+1][n2+1];//默认初始化为0int result=0;for(int i=1;i<=n1;i++){for(int j=1;j<=n2;j++){if(nums1[i-1]==nums2[j-1]){dp[i][j]=dp[i-1][j-1]+1;}else{dp[i][j]=Math.max(dp[i-1][j],dp[i][j-1]);}}}return dp[n1][n2];}
}
3.1035. 不相交的线
链接: 1035. 不相交的线

class Solution {//和上一题一摸一样,求最长公共子序列public int maxUncrossedLines(int[] nums1, int[] nums2) {int n1=nums1.length;int n2=nums2.length;int dp[][]=new int[n1+1][n2+1];//默认初始化为0int result=0;for(int i=1;i<=n1;i++){for(int j=1;j<=n2;j++){if(nums1[i-1]==nums2[j-1]){dp[i][j]=dp[i-1][j-1]+1;}else{dp[i][j]=Math.max(dp[i-1][j],dp[i][j-1]);}}}return dp[n1][n2];}
}
2.子序列(连续)
1.674. 最长连续递增序列
链接: 674. 最长连续递增序列
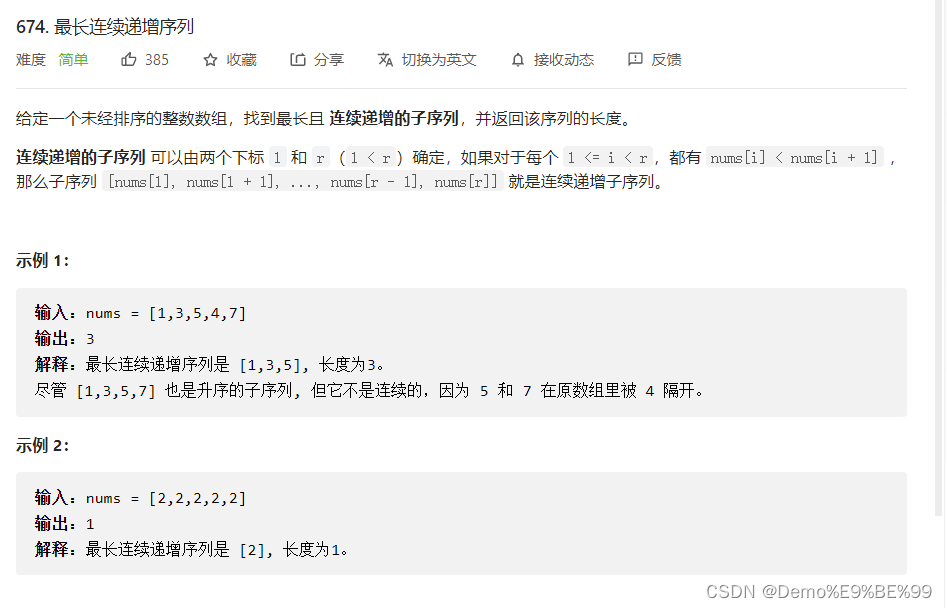
class Solution {public int findLengthOfLCIS(int[] nums) {int n=nums.length;if(n<=1){return n;}int dp[]=new int[n];for(int i=0;i<n;i++){dp[i]=1;}int result=0;for(int i=1;i<n;i++){if(nums[i]>nums[i-1]){dp[i]=dp[i-1]+1;}result=Math.max(result,dp[i]);}return result;}
}
*2.718. 最长重复子数组
链接: 718. 最长重复子数组
class Solution {public int findLength(int[] nums1, int[] nums2) {int n1=nums1.length;int n2=nums2.length;int dp[][]=new int[n1+1][n2+1];//默认初始化为0int result=0;for(int i=1;i<=n1;i++){for(int j=1;j<=n2;j++){if(nums1[i-1]==nums2[j-1]){dp[i][j]=dp[i-1][j-1]+1;}result=Math.max(result,dp[i][j]);}}return result;}
}
3.53. 最大子数组和
链接: 53. 最大子数组和
class Solution {public int maxSubArray(int[] nums) {int n=nums.length;int dp[]=new int [n];dp[0]=nums[0];int result=dp[0];for(int i=1;i<n;i++){dp[i]=Math.max(dp[i-1]+nums[i],nums[i]);result=Math.max(dp[i],result);}return result;}
}
3.编辑距离
1.392. 判断子序列
链接: 392. 判断子序列
class Solution {public boolean isSubsequence(String s, String t) {char []nums1=s.toCharArray();char []nums2=t.toCharArray();int n1=nums1.length;int n2=nums2.length;int dp[][]=new int[n1+1][n2+1];//默认初始化为0for(int i=1;i<=n1;i++){for(int j=1;j<=n2;j++){if(nums1[i-1]==nums2[j-1]){dp[i][j]=dp[i-1][j-1]+1;}else{dp[i][j]=dp[i][j-1];}}}if(dp[n1][n2]==n1){return true;}return false;}
}
2.115. 不同的子序列
链接: 115. 不同的子序列
class Solution {public int numDistinct(String s, String t) {int n1=s.length();int n2=t.length();int [][]dp=new int[n1+1][n2+1];//默认为0for(int i=0;i<n1;i++){dp[i][0]=1;}for(int i=1;i<=n1;i++){for(int j=1;j<=n2;j++){if (j > i)continue;if(s.charAt(i-1)==t.charAt(j-1)){dp[i][j]=dp[i-1][j-1]+dp[i-1][j];}else{dp[i][j]=dp[i-1][j];}}}return dp[n1][n2];}
}
3.583. 两个字符串的删除操作
链接: 583. 两个字符串的删除操作
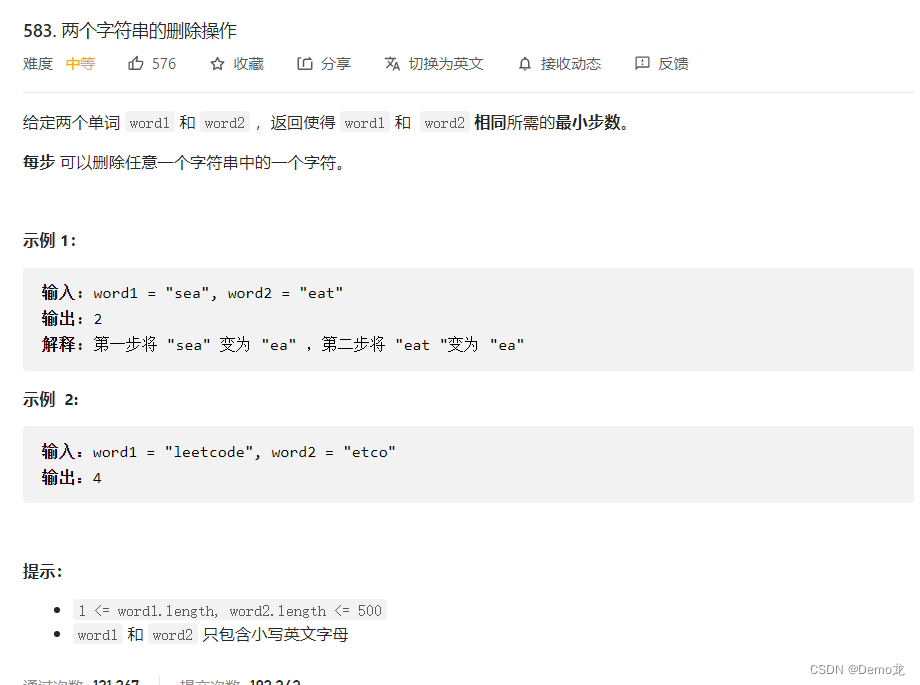
方法一,动态规划思路解决
class Solution {public int minDistance(String word1, String word2) {int n1=word1.length();int n2=word2.length();int [][]dp=new int[n1+1][n2+1];//默认为0for(int i=0;i<=n1;i++){dp[i][0]=i;}for(int j=0;j<=n2;j++){dp[0][j]=j;}for(int i=1;i<=n1;i++){for(int j=1;j<=n2;j++){if(word1.charAt(i-1)==word2.charAt(j-1)){dp[i][j]=dp[i-1][j-1];}else{dp[i][j]=Math.min(dp[i-1][j-1]+2,Math.min(dp[i-1][j]+1,dp[i][j-1]+1));}}}return dp[n1][n2];}
}
方法二,求公共最大子序列,len1+len2-最大子序列长度即为需要删除的数目
//方法二
class Solution {public int minDistance(String word1, String word2) {int n1=word1.length();int n2=word2.length();int dp[][]=new int[n1+1][n2+1];//默认初始化为0int result=0;for(int i=1;i<=n1;i++){for(int j=1;j<=n2;j++){if(word1.charAt(i-1)==word2.charAt(j-1)){dp[i][j]=dp[i-1][j-1]+1;}else{dp[i][j]=Math.max(dp[i-1][j],dp[i][j-1]);}}}return n1+n2-2*dp[n1][n2];}
}
4.72. 编辑距离
链接: 72. 编辑距离
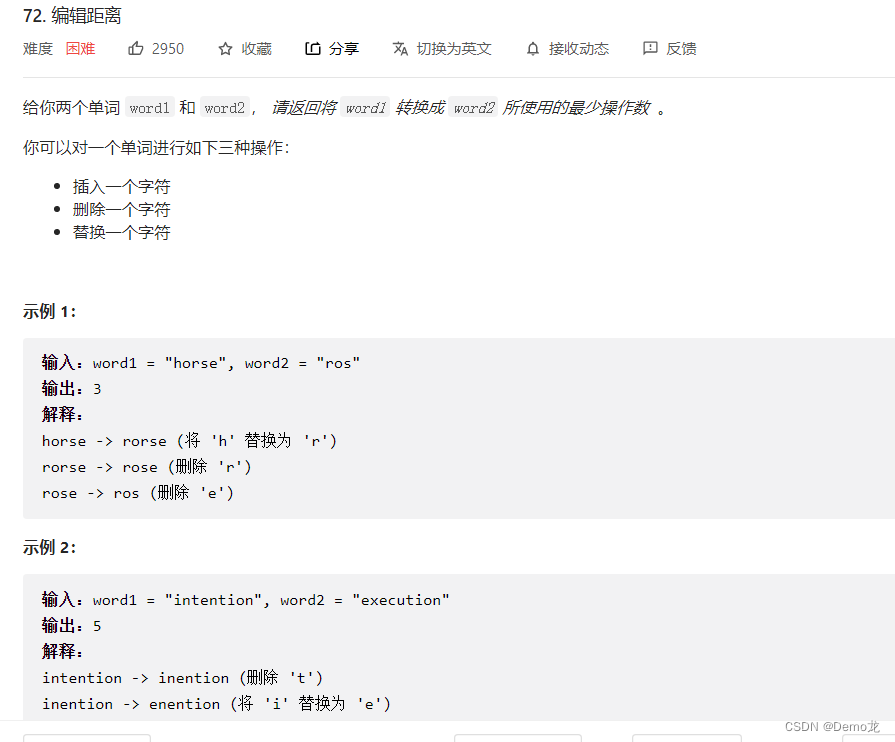
class Solution {public int minDistance(String word1, String word2) {int n1=word1.length();int n2=word2.length();int [][]dp=new int[n1+1][n2+1];//默认为0for(int i=0;i<=n1;i++){dp[i][0]=i;}for(int j=0;j<=n2;j++){dp[0][j]=j;}for(int i=1;i<=n1;i++){for(int j=1;j<=n2;j++){if(word1.charAt(i-1)==word2.charAt(j-1)){dp[i][j]=dp[i-1][j-1];}else{dp[i][j]=Math.min(dp[i-1][j-1]+1,Math.min(dp[i-1][j]+1,dp[i][j-1]+1));}}}return dp[n1][n2];}
}
4.回文
1.647. 回文子串
链接: 647. 回文子串
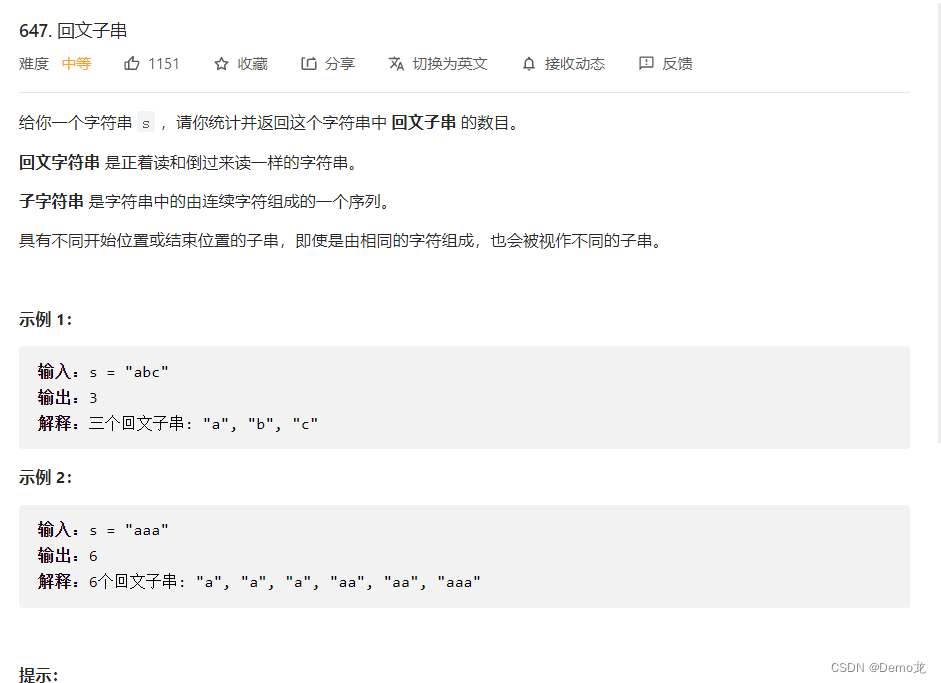
class Solution {public int countSubstrings(String s) {int n=s.length();int dp[][]=new int[n+1][n+1];int result=0;for(int i=n-1;i>=0;i--){for(int j=i;j<n;j++){if(s.charAt(i)==s.charAt(j)){if(j-i<=1){dp[i][j]=1;result++;}else if(dp[i+1][j-1]==1){dp[i][j]=1;result++;}}}}return result;}
}
2.516. 最长回文子序列
链接: 516. 最长回文子序列
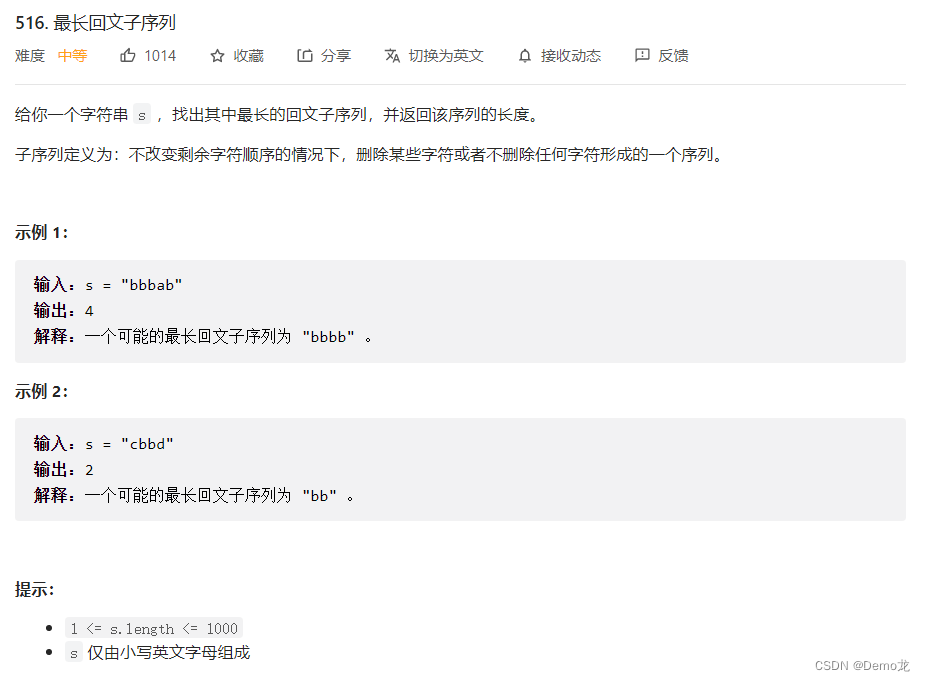
class Solution {public int longestPalindromeSubseq(String s) {int n=s.length();int dp[][]=new int[n+1][n+1];for(int i=0;i<n;i++){dp[i][i]=1;}for(int i=n-1;i>=0;i--){for(int j=i+1;j<n;j++){if(s.charAt(i)==s.charAt(j)){dp[i][j]=dp[i+1][j-1]+2;}else {dp[i][j]=Math.max(dp[i+1][j],dp[i][j-1]);}}}return dp[0][n-1];}
}
相关文章:

动态规划算法——40道leetcode实例入门到熟练
目录 t0.解题五部曲1.基础入门题目1.509. 斐波那契数2.70. 爬楼梯3.746. 使用最小花费爬楼梯4.62. 不同路径5.63. 不同路径 II6.343. 整数拆分7.96. 不同的二叉搜索树 2.背包问题1.01背包(二维数组实现)2.01背包(滚动数组实现)1.4…...

Nmap入门到高级【第十一章】
预计更新第一章. Python 简介 Python 简介和历史Python 特点和优势安装 Python 第二章. 变量和数据类型 变量和标识符基本数据类型:数字、字符串、布尔值等字符串操作列表、元组和字典 第三章. 控制语句和函数 分支结构:if/else 语句循环结构&#…...
配置本地Angular环境并使用VsCode调试Angular前端项目
配置本地Angular环境并使用VsCode调试Angular前端项目 配置本地Angular环境部署Node.Js本地环境配置一下环境变量 使用vscode调试Angular安装vscode 配置本地Angular环境 部署Node.Js本地环境 1 从官网下载node.js, 本文为(v16.13.0) 下载地址: https://nodejs.org/dist/v16.…...

100ASK_全志V853-PRO开发板支持人形检测和人脸识别
1.前言 V853 芯片内置一颗 NPU核,其处理性能为最大 1 TOPS 并有 128KB 内部高速缓存用于高速数据交换,支持 OpenCL、OpenVX、android NN 与 ONNX 的 API 调用,同时也支持导入大量常用的深度学习模型。本章提供一个例程,展示如何使…...

简单实现基于UDP与TCP的回显服务器
目录 前言UDP 版的回显服务器需要用到的 api服务端客户端UDP 版本的字典客户端和字典服务器 TCP 版的回显服务器需要用到的 api服务器客户端对服务器进行改进(使用线程池)TCP 版本的字典客户端和字典服务器 前言 我们写网络程序, 主要编写的是应用层代码. 真正要发送这个数据,…...

家用洗地机有什么推荐的吗?家用洗地机哪款好
洗地机是创新、高效的清洁工具,其具有高性能的清洁能力和卓越的操作体验。与传统的清洁工具相比,洗地机可以迅速而彻底地打扫地面,降低清洁时间和人力成本,让我们在工作之余不用花费大量的时间和精力去打扫卫生,下面就…...

深度学习与文本聚类:一篇全面的介绍与实践指南
❤️觉得内容不错的话,欢迎点赞收藏加关注😊😊😊,后续会继续输入更多优质内容❤️ 👉有问题欢迎大家加关注私戳或者评论(包括但不限于NLP算法相关,linux学习相关,读研读博…...
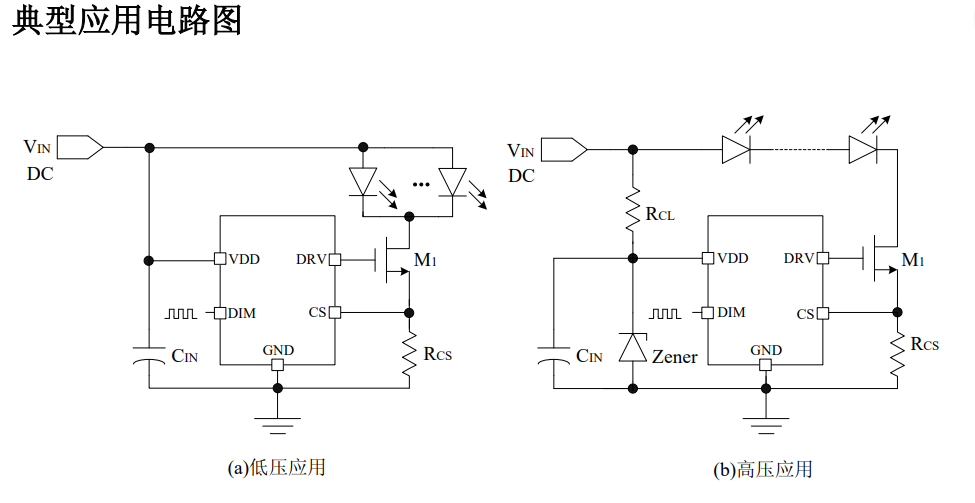
AP5153 线性降压恒流驱动芯片 2.5A
AP5153 是一种 PWM 调光的、低压 差的 LED 线性降压恒流驱动器。 AP5153 仅需要外接一个电阻和一个 NMOS 管就可以构成一个完整的 LED 恒 流驱动电路, 调节该外接电阻就可以调节 输出电流,输出电流可调范围为 20mA 到 3.0A。 AP5153 还可以通过在 DIM…...
)
Unity物理系统脚本编程(下)
一、修改物理材质 Unity对物体表面材料的性质做了件化处理,仅有5种常用属性: Dynamic Friction(动态摩擦系数)Static Friction(静态摩擦系数)Bounciness(弹性系数)Friction Combine…...

容器技术的发展
容器技术的发展 近年来,随着计算机硬件、网络以及云计算等技术的迅速发展,云原生的概念也越来越受到业界人士的广泛关注,越来越多的应用场景开始拥抱云原生,其中容器技术的发展起着至关重要的作用。本章将介绍容器技术的基础知识…...

Python Flask request中常见存储参数的介绍
Python Flask request中常见存储参数的介绍 首先从flask模块中导入请求对象: from flask import requestrequest.form 通过method属性可以操作当前请求方法,通过使用form属性处理表单数据(本质也是得到一个字典,如果传输的是字…...

php+vue网盘系统的设计与实现
该网盘系统的开发和设计根据用户的实际情况出发,对系统的需求进行了详细的分析,然后进行系统的整体设计,最后通过测试使得系统设计的更加完整,可以实现系统中所有的功能,在开始编写论文之前亲自到图书馆借阅php书籍&am…...
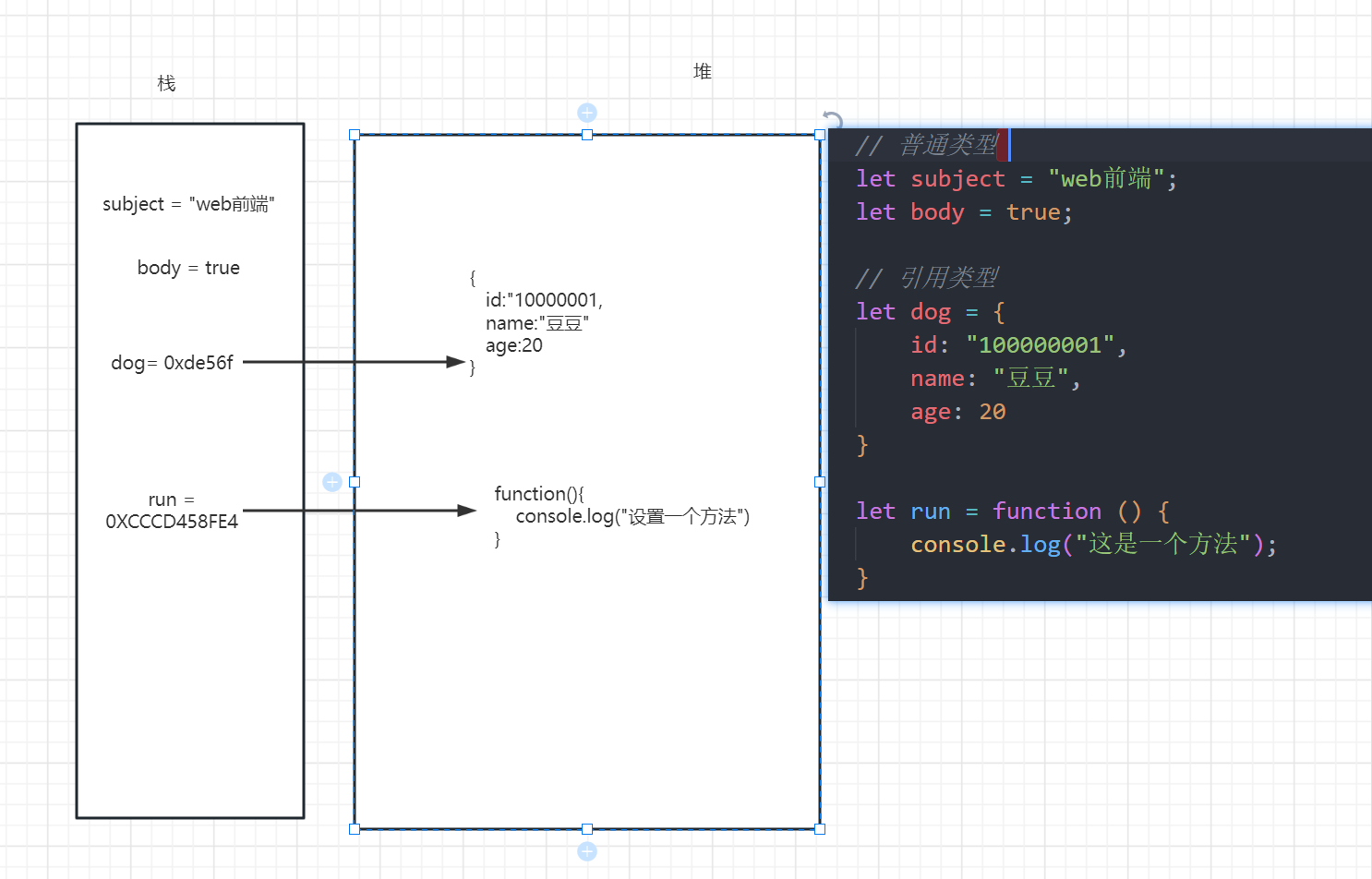
[前端]深浅拷贝
一、回顾变量类型 基础类型 boolean(bool) number string null undefined 引用类型 object function array 基本类型与引用类型的存储 基本类型一般存储在 栈 (栈小) 栈一旦确认 大小就固定 可能会造成溢出栈一般是先进后出用于存储…...

文章纠错免费软件-文字校对软件免费下载
自动校对稿件的软件 自动校对稿件的软件是一种基于自然语言处理(Natural Language Processing, NLP)和机器学习(Machine Learning)技术的工具,可以较为准确地检测和纠正文本中出现的语法、拼写、标点符号以及其他笔误…...

【Redis】Redis缓存雪崩、缓存穿透、缓存击穿(热key问题)
目录 一、缓存穿透 1、概念 2、解决办法 1.缓存空对象 2.布隆过滤 二、缓存雪崩 1、概念 2、解决办法 1.给key设置随机的过期时间TTL 2.业务添加多级缓存 3.利用集群提供服务可用性 4.缓存业务添加降级限流 三、缓存击穿 1、概念 2、解决办法 1.互斥锁 2.逻辑…...

为什么很多程序员喜欢linux系统?
a> Linux哪些行业在运用? Linux系统运用极其广泛,不少用户只知道windows,是因为,Linux的运用主要是在企业端。现在科技极其发达,我们手机在手,就能干很多事情,只需点一点屏幕,轻松…...
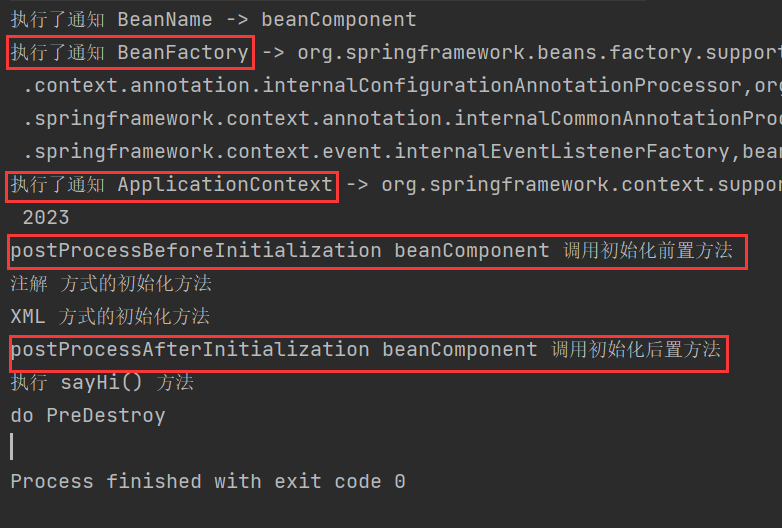
Bean 作用域和生命周期
✏️作者:银河罐头 📋系列专栏:JavaEE 🌲“种一棵树最好的时间是十年前,其次是现在” 目录 lombok的使用案例引入作用域定义singleton单例作用域prototype原型作用域(多例作用域)request请求作用域session会话作用域ap…...

PMP考试常见13个固定套路
一、变更批准之后 变更批准后要做三件事: 1、在变更日志中记录 2、通知相关干系人 3、更新项目管理计划 二、风险的情景题 1、先判断风险识别了,还是风险发生了。 2、若是风险识别,按风险管理程序走; 3、若是风险发生,则应采取应急措施…...
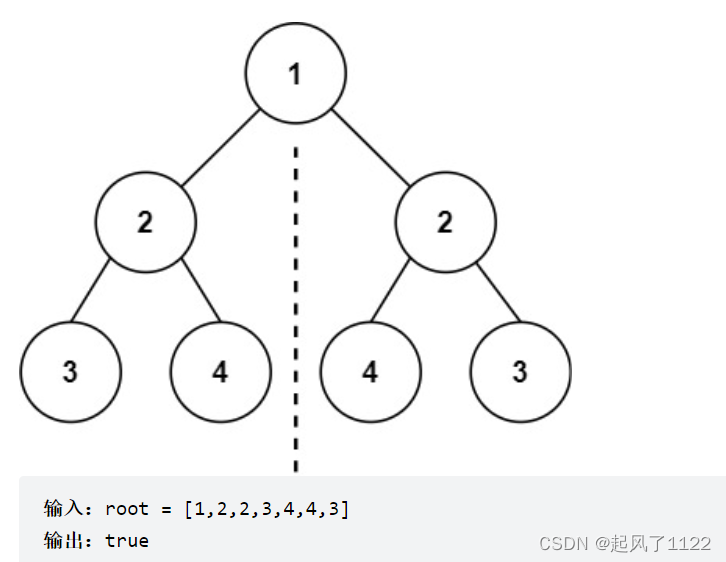
Leecode101 ——对称二叉树
对称二叉树:Leecode 101 leecode 101 对称二叉树 根据题目描述,首先想清楚,对称二叉树要比较的是哪两个节点。对于二叉树是否对称,要比较的是根节点的左子树与根节点的右子树是不是相互翻转的,其实也就是比较两个树,…...
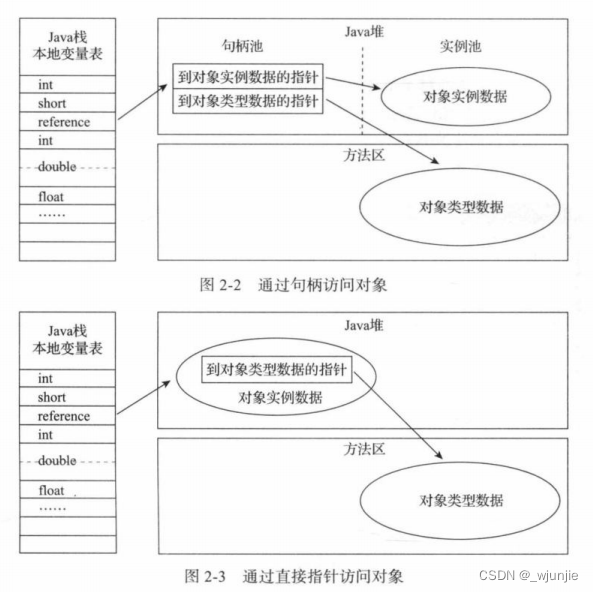
JVM学习随笔03——Java堆中new一个对象的步骤
目录 一、进行类加载 二、堆中分配内存 1、怎么输出GC日志: 2、内存分配的两种方式: 3、内存分配过程中并发控制的两种方式: 三、内存空间初始化 四、对象头初始化(对象头包含哪些信息?) 五、执行构…...
)
Java 语言特性(面试系列2)
一、SQL 基础 1. 复杂查询 (1)连接查询(JOIN) 内连接(INNER JOIN):返回两表匹配的记录。 SELECT e.name, d.dept_name FROM employees e INNER JOIN departments d ON e.dept_id d.dept_id; 左…...

Appium+python自动化(十六)- ADB命令
简介 Android 调试桥(adb)是多种用途的工具,该工具可以帮助你你管理设备或模拟器 的状态。 adb ( Android Debug Bridge)是一个通用命令行工具,其允许您与模拟器实例或连接的 Android 设备进行通信。它可为各种设备操作提供便利,如安装和调试…...

线程与协程
1. 线程与协程 1.1. “函数调用级别”的切换、上下文切换 1. 函数调用级别的切换 “函数调用级别的切换”是指:像函数调用/返回一样轻量地完成任务切换。 举例说明: 当你在程序中写一个函数调用: funcA() 然后 funcA 执行完后返回&…...

vue3 定时器-定义全局方法 vue+ts
1.创建ts文件 路径:src/utils/timer.ts 完整代码: import { onUnmounted } from vuetype TimerCallback (...args: any[]) > voidexport function useGlobalTimer() {const timers: Map<number, NodeJS.Timeout> new Map()// 创建定时器con…...

NFT模式:数字资产确权与链游经济系统构建
NFT模式:数字资产确权与链游经济系统构建 ——从技术架构到可持续生态的范式革命 一、确权技术革新:构建可信数字资产基石 1. 区块链底层架构的进化 跨链互操作协议:基于LayerZero协议实现以太坊、Solana等公链资产互通,通过零知…...

Linux --进程控制
本文从以下五个方面来初步认识进程控制: 目录 进程创建 进程终止 进程等待 进程替换 模拟实现一个微型shell 进程创建 在Linux系统中我们可以在一个进程使用系统调用fork()来创建子进程,创建出来的进程就是子进程,原来的进程为父进程。…...

零基础在实践中学习网络安全-皮卡丘靶场(第九期-Unsafe Fileupload模块)(yakit方式)
本期内容并不是很难,相信大家会学的很愉快,当然对于有后端基础的朋友来说,本期内容更加容易了解,当然没有基础的也别担心,本期内容会详细解释有关内容 本期用到的软件:yakit(因为经过之前好多期…...

计算机基础知识解析:从应用到架构的全面拆解
目录 前言 1、 计算机的应用领域:无处不在的数字助手 2、 计算机的进化史:从算盘到量子计算 3、计算机的分类:不止 “台式机和笔记本” 4、计算机的组件:硬件与软件的协同 4.1 硬件:五大核心部件 4.2 软件&#…...

【 java 虚拟机知识 第一篇 】
目录 1.内存模型 1.1.JVM内存模型的介绍 1.2.堆和栈的区别 1.3.栈的存储细节 1.4.堆的部分 1.5.程序计数器的作用 1.6.方法区的内容 1.7.字符串池 1.8.引用类型 1.9.内存泄漏与内存溢出 1.10.会出现内存溢出的结构 1.内存模型 1.1.JVM内存模型的介绍 内存模型主要分…...

手机平板能效生态设计指令EU 2023/1670标准解读
手机平板能效生态设计指令EU 2023/1670标准解读 以下是针对欧盟《手机和平板电脑生态设计法规》(EU) 2023/1670 的核心解读,综合法规核心要求、最新修正及企业合规要点: 一、法规背景与目标 生效与强制时间 发布于2023年8月31日(OJ公报&…...
