当前位置： 首页 > news >正文

React 组件

news 2025/11/9 22:20:22

文章目录

  • React 组件
  • 复合组件

React 组件

在这里插入图片描述

本节将讨论如何使用组件使得我们的应用更容易来管理。

接下来我们封装一个输出 “Hello World！” 的组件，组件名为 HelloMessage：

React 实例

<!DOCTYPE html>
<html>
<head>
<meta charset="UTF-8" />
<title>React 实例</title>
<script src="http://cdn.bootcss.com/react/15.4.2/react.min.js"></script>
<script src="http://cdn.bootcss.com/react/15.4.2/react-dom.min.js"></script>
<script src="http://cdn.bootcss.com/babel-standalone/6.22.1/babel.min.js"></script>
</head>
<body>
<div id="example"></div>
<script type="text/babel">var HelloMessage = React.createClass({render: function() {return <h1>Hello World！</h1>;}});ReactDOM.render(<HelloMessage />,document.getElementById('example'));</script>
</body>
</html>

运行效果：
在这里插入图片描述

实例解析：

React.createClass 方法用于生成一个组件类 HelloMessage。

<HelloMessage /> 实例组件类并输出信息。

注意：原生 HTML 元素名以小写字母开头，而自定义的 React 类名以大写字母开头，比如 HelloMessage 不能写成 helloMessage。除此之外还需要注意组件类只能包含一个顶层标签，否则也会报错。

如果我们需要向组件传递参数，可以使用 this.props 对象,实例如下：

React 实例

<!DOCTYPE html>
<html>
<head>
<meta charset="UTF-8" />
<title>React 实例</title>
<script src="http://cdn.bootcss.com/react/15.4.2/react.min.js"></script>
<script src="http://cdn.bootcss.com/react/15.4.2/react-dom.min.js"></script>
<script src="http://cdn.bootcss.com/babel-standalone/6.22.1/babel.min.js"></script>
</head>
<body>
<div id="example"></div>
<script type="text/babel">var HelloMessage = React.createClass({render: function() {return <h1>Hello {this.props.name}</h1>;}});ReactDOM.render(<HelloMessage name="www.csdn.net" />,document.getElementById('example'));</script>
</body>
</html>

运行效果：
在这里插入图片描述

以上实例中 name 属性通过 this.props.name 来获取。

注意：在添加属性时， class 属性需要写成 className ，for 属性需要写成 htmlFor ，这是因为 class 和 for 是 JavaScript 的保留字。

复合组件

我们可以通过创建多个组件来合成一个组件，即把组件的不同功能点进行分离。

以下实例我们实现了输出网站名字和网址的组件：

React 实例

<!DOCTYPE html>
<html>
<head>
<meta charset="UTF-8" />
<title>React 实例</title>
<script src="http://cdn.bootcss.com/react/15.4.2/react.min.js"></script>
<script src="http://cdn.bootcss.com/react/15.4.2/react-dom.min.js"></script>
<script src="http://cdn.bootcss.com/babel-standalone/6.22.1/babel.min.js"></script>
</head>
<body>
<div id="example"></div>
<script type="text/babel">var WebSite = React.createClass({render: function() {return (<div><Name name={this.props.name} /><Link site={this.props.site} /></div>);}
});var Name = React.createClass({render: function() {return (<h1>{this.props.name}</h1>);}
});var Link = React.createClass({render: function() {return (<a href={this.props.site}>{this.props.site}</a>);}
});ReactDOM.render(<WebSite name="CSDN" site=" http://www.csdn.net" />,document.getElementById('example')
);</script>
</body>
</html>

实例中 WebSite 组件使用了 Name 和 Link 组件来输出对应的信息，也就是说 WebSite 拥有 Name 和 Link 的实例。

相关文章：

React 组件

文章目录 React 组件复合组件 React 组件 本节将讨论如何使用组件使得我们的应用更容易来管理。 接下来我们封装一个输出 “Hello World&#xff01;” 的组件&#xff0c;组件名为 HelloMessage&#xff1a; React 实例 <!DOCTYPE html> <html> <head> &…...

编程日记 2023/5/11 15:25:40

硕士学位论文的几种常见节奏

摘要: 本文描述硕士学位论文的几种目录结构, 特别针对机器学习方向. 1. 基础版 XX算法及其在YY中的应用 针对情况: 只有一篇小论文支撑. 第 1 章: 引言 ( > 5页) 1.1 背景及意义 (应用背景、研究意义, 2 页) 1.2 研究进展及趋势 (算法方面, 2 页) 1.3 论文结构 (1 页) 第 …...

编程日记 2023/5/11 15:20:39

找兄弟单词

描述 定义一个单词的“兄弟单词”为&#xff1a;交换该单词字母顺序&#xff08;注&#xff1a;可以交换任意次&#xff09;&#xff0c;而不添加、删除、修改原有的字母就能生成的单词。 兄弟单词要求和原来的单词不同。例如&#xff1a; ab 和 ba 是兄弟单词。 ab 和 ab 则不…...

编程日记 2023/6/1 8:36:57

python字典翻转教学

目录 第1关 创建大学英语四级单词字典 第2关 合并大学英语四六级词汇字典 第3关 查单词输出中文释义 第4关 删除字典中特定字母开头的单词 第5关 单词英汉记忆训练 第1关 创建大学英语四级单词字典 本关任务&#xff1a;编写一个能创建大学英语四级单词字典的小程序。 测…...

编程日记 2023/5/11 15:10:36

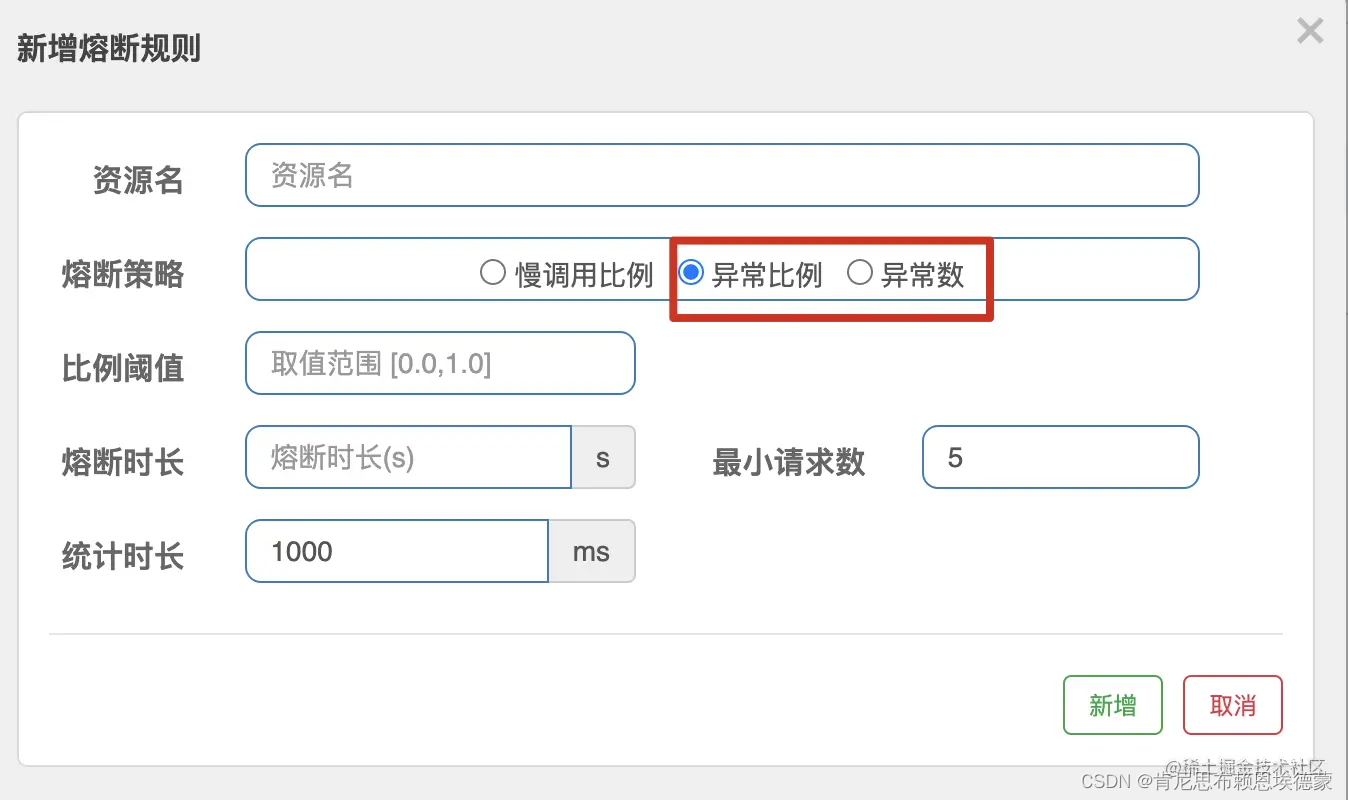
sentinel 随笔 3-降级处理

0. 像喝点东西&#xff0c;但不知道喝什么 先来段源码&#xff0c;看一下 我们在dashboard 录入的降级规则&#xff0c;都映射到哪些字段上 package com.alibaba.csp.sentinel.slots.block.degrade;public class DegradeRule extends AbstractRule {public DegradeRule(String…...

编程日记 2023/5/11 15:05:35

如何解决IP能ping通但无法上网的问题？

当我们在网络环境中遇到无法上网的问题时&#xff0c;可能会尝试使用ping命令来测试网络连接是否正常。如果ping测试成功&#xff0c;说明我们的IP地址能够和网络中其他设备进行通信&#xff0c;但是无法上网。这种情况下&#xff0c;我们需要采取一些措施来解决这个问题。本文…...

编程日记 2023/5/11 15:00:33

Autosar实践-CANTp

文章目录 前言一、CanTp是什么？二、Autosar配置三、诊断数据传输流程1.接收单帧失败，上层没有适当的buffer2.成功接收单帧3.成功发送单帧4.成功接收多帧5.成功发送多帧前言 CANTp模块作为提供数据拆包、组包、流控制传输的服务，在Autosar基础软件通信中起着至关重要的作用。…...

编程日记 2023/5/11 14:55:32

Redis简介

Redis&#xff08;Remote Dictionary Server&#xff09;是一个开源的键值对&#xff08;key-value&#xff09;数据库&#xff0c;支持网络、可基于内存亦可持久化。 Redis的数据结构包括列表&#xff08;List&#xff09;、集合&#xff08;Set&#xff09;、有序集合&#…...

编程日记 2023/5/11 14:50:26

报错问题修改

Vue 项目报错&#xff1a;‘$‘ is not defined ( no-undef ) 错误原因是不认识 $ 符&#xff0c;他是 JQuery 中得符号&#xff0c;引入了 JQuery 文件里的函数报错onclick is not defined问题(作用域问题) window.onload function (){ onload function (){ 第二种方法…...

编程日记 2023/5/11 14:45:25

专访惠众科技｜元宇宙应用如何借助3DCAT实时云渲染实现流畅大并发呈现？

当前互联网流量红利已经逐渐消失&#xff0c;营销同质化愈发严重。在这样的背景下&#xff0c;催生了以为元宇宙 焦点的虚拟产业经济。元宇宙在各行各业中以不同形式快速萌生、成长&#xff0c;呈现出多元化的应用场景。尤其是众多品牌&#xff0c;将元宇宙视为品牌建设与营销新…...

编程日记 2023/5/11 14:40:24

加速开放计算产业化，OCTC五大原则瞄准需求痛点

回顾计算产业过去十余载的历程&#xff0c;开放计算始终是一个绕不开的核心焦点。 始于2011年Facebook发起的数据中心硬件开源项目--开放计算项目&#xff08;简称&#xff1a;OCP&#xff09;&#xff0c;开放计算犹如星星之火&#xff0c;不仅迅速形成燎原之势&#xff0c;更…...

编程日记 2023/5/11 14:35:23

【RabbitMQ】安装及六种模式

文章目录 安装rabbitmq镜像访问容器内部15672端口映射到外面的端口地址RabbitMQ六种模式Hello world模式Work queues模式Publish/Subscribe模式交换机fanout类型 Routing模式Topics模式RPC模式 rabbitmq&#xff1a;0->1的学习 学习文档&#xff1a;https://www.cnblogs.com…...

编程日记 2023/5/11 14:30:22

数据结构刷题（三十一）：1049. 最后一块石头的重量 II、完全背包理论、518零钱兑换II

一、1049. 最后一块石头的重量 II 1.思路&#xff1a;01背包问题&#xff0c;其中dp[j]表示容量为j的背包&#xff0c;最多可以背最大重量为dp[j]。 2.注意&#xff1a;递推公式dp[j] max(dp[j], dp[j - stones[i]] stones[i]);本题中的重量就是价值&#xff0c;所以第二个…...

编程日记 2023/5/11 14:25:21

opencv_c++学习（四）

图像在opencv中的存储方式 在上图中可以看出&#xff0c;在opencv中采用的是像素值来代表每一个像素三通道颜色的深浅。 Mat对象 Mat对象是在OpenCV2.0之后引进的图像数据结构、自动分配内存、不存在内存泄漏的问题&#xff0c;是面向对象的数据结构。分了两个部分&#xff0…...

编程日记 2023/5/11 14:20:20

基于AT89C51单片机的篮球计时记分设计

点击链接获取Keil源码与Project Backups仿真图： https://download.csdn.net/download/qq_64505944/87771065 源码获取 主要内容： 基于51单片机设计篮球计时计分器，结合单片机串行接口原理，用AT89C51设计一个篮球比赛计分计时器，能够通过数码管显示分数和比赛时间（并设有…...

编程日记 2023/5/11 14:15:19

并发编程-Day2

并发编程 1.共享模型-内存 共享变量在多线程间的<可见性>问题与多条指令执行时的<有序性>问题 1.1Java内存模型 JMM它定义了主存、工作内存抽象概念,底层对应着CPU寄存器、缓存、硬件内存CPU指令优化等. JMM体现在&#xff1a; 原子性-保证指令不会受到线程上…...

编程日记 2023/5/11 14:10:18

第1章 Nginx简介

基于 Nginx版本 1.14.2 &#xff0c;Tomcat版本 9.0.0 演示 第1章 Nginx简介 1.1 Nginx发展介绍 Nginx &#xff08;engine x&#xff09; 是一个高性能的Web服务器和反向代理服务器&#xff0c;也可以作为邮件代理服务器。 Nginx 特点是占有内存少&#xff0c;并发处理能力…...

编程日记 2023/5/11 14:05:16

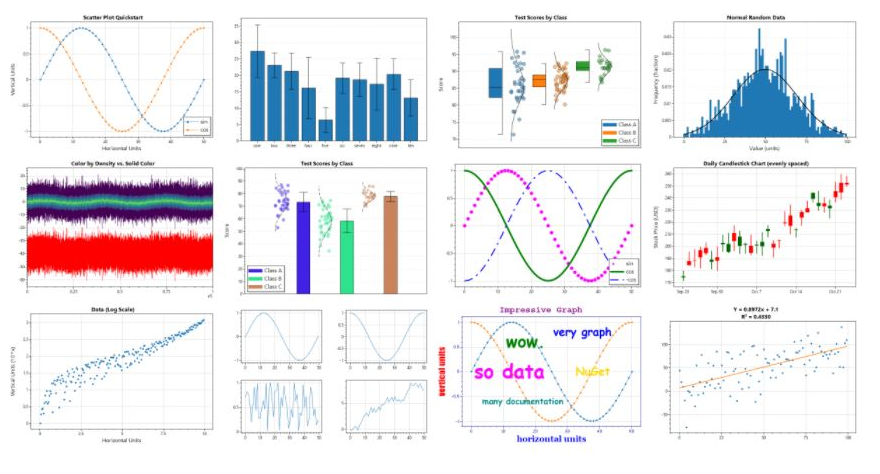
一个.Net功能强大、易于使用、跨平台开源可视化图表

可视化图表运用是非常广泛的&#xff0c;比如BI系统、报表统计等。但是针对桌面应用的应用&#xff0c;很多报表都是收费的&#xff0c;今天给大家推荐一个免费.Net可视化开源的项目&#xff01; 项目简介 基于C#开发的功能强大、易于使用、跨平台高质量的可视化图表库&#…...

编程日记 2023/5/11 14:00:15

浅谈 ext2 文件系统的特点、优缺点以及使用场景

ext2&#xff08;Extended File System 2&#xff09;是 Linux 中最早的一种文件系统&#xff0c;它是 Linux 文件系统的基础&#xff0c;也被广泛用于其他类 Unix 系统中。下面是 ext2 文件系统的特点、优缺点以及使用场景&#xff1a; 特点&#xff1a; ext2 文件系统可以支…...

编程日记 2023/5/11 13:55:15

Map和Set数据结构和ES6模块化语法

Map和Set数据结构 ●ES6 新增的两种数据结构 ●共同的特点: 不接受重复数据 Set数据结构 ●是一个 类似于 数组的数据结构 ●按照索引排列的数据结构 创建 Set 数据结构 语法: var s new Set([ 数据1, 数据2, 数据3, ... ]) Set 数据结构的属性和方法 ●size 属性 ○语法: 数…...

编程日记 2023/5/11 13:50:14

大数据学习栈记——Neo4j的安装与使用

本文介绍图数据库Neofj的安装与使用&#xff0c;操作系统&#xff1a;Ubuntu24.04&#xff0c;Neofj版本&#xff1a;2025.04.0。 Apt安装 Neofj可以进行官网安装&#xff1a;Neo4j Deployment Center - Graph Database & Analytics 我这里安装是添加软件源的方法 最新版…...

编程新知 2025/11/9 6:34:57

大话软工笔记—需求分析概述

需求分析&#xff0c;就是要对需求调研收集到的资料信息逐个地进行拆分、研究&#xff0c;从大量的不确定“需求”中确定出哪些需求最终要转换为确定的“功能需求”。 需求分析的作用非常重要&#xff0c;后续设计的依据主要来自于需求分析的成果&#xff0c;包括: 项目的目的…...

编程新知 2025/11/7 14:08:13

中南大学无人机智能体的全面评估！BEDI：用于评估无人机上具身智能体的综合性基准测试

作者&#xff1a;Mingning Guo, Mengwei Wu, Jiarun He, Shaoxian Li, Haifeng Li, Chao Tao单位&#xff1a;中南大学地球科学与信息物理学院论文标题&#xff1a;BEDI: A Comprehensive Benchmark for Evaluating Embodied Agents on UAVs论文链接&#xff1a;https://arxiv.…...

编程新知 2025/11/8 22:34:22

在rocky linux 9.5上在线安装 docker

前面是指南&#xff0c;后面是日志 sudo dnf config-manager --add-repo https://download.docker.com/linux/centos/docker-ce.repo sudo dnf install docker-ce docker-ce-cli containerd.io -y docker version sudo systemctl start docker sudo systemctl status docker …...

编程新知 2025/7/27 10:03:12

大语言模型如何处理长文本？常用文本分割技术详解

为什么需要文本分割？ 引言：为什么需要文本分割？一、基础文本分割方法1. 按段落分割（Paragraph Splitting）2. 按句子分割（Sentence Splitting）二、高级文本分割策略3. 重叠分割（Sliding Window）4. 递归分割（Recursive Splitting）三、生产级工具推荐5. 使用LangChain的…...

编程新知 2025/10/20 5:24:23

【git】把本地更改提交远程新分支feature_g

创建并切换新分支 git checkout -b feature_g 添加并提交更改 git add . git commit -m “实现图片上传功能” 推送到远程 git push -u origin feature_g...

编程新知 2025/8/15 18:53:03

什么是EULA和DPA

文章目录 EULA&#xff08;End User License Agreement&#xff09;DPA&#xff08;Data Protection Agreement&#xff09;一、定义与背景二、核心内容三、法律效力与责任四、实际应用与意义 EULA&#xff08;End User License Agreement&#xff09; 定义&#xff1a; EULA即…...

编程新知 2025/10/18 7:13:10

土地利用/土地覆盖遥感解译与基于CLUE模型未来变化情景预测；从基础到高级，涵盖ArcGIS数据处理、ENVI遥感解译与CLUE模型情景模拟等

&#x1f50d; 土地利用/土地覆盖数据是生态、环境和气象等诸多领域模型的关键输入参数。通过遥感影像解译技术&#xff0c;可以精准获取历史或当前任何一个区域的土地利用/土地覆盖情况。这些数据不仅能够用于评估区域生态环境的变化趋势&#xff0c;还能有效评价重大生态工程…...

编程新知 2025/9/12 15:10:44

.Net Framework 4/C# 关键字（非常用，持续更新...）

一、is 关键字 is 关键字用于检查对象是否于给定类型兼容，如果兼容将返回 true，如果不兼容则返回 false，在进行类型转换前，可以先使用 is 关键字判断对象是否与指定类型兼容，如果兼容才进行转换，这样的转换是安全的。 例如有：首先创建一个字符串对象，然后将字符串对象隐…...

编程新知 2025/9/25 18:41:38

Mysql中select查询语句的执行过程

目录 1、介绍 1.1、组件介绍 1.2、Sql执行顺序 2、执行流程 2.1. 连接与认证 2.2. 查询缓存 2.3. 语法解析&#xff08;Parser&#xff09; 2.4、执行sql 1. 预处理&#xff08;Preprocessor&#xff09; 2. 查询优化器&#xff08;Optimizer&#xff09; 3. 执行器…...

编程新知 2025/11/7 7:59:43