【YOLO 系列】YOLO v4-v5先验知识
文章目录
- 输入端
- Mosaic数据增强
- Self-Adversarial Training
- CmBN
- 主干网络
- Mish激活函数
- DropBlock 正则化
- CSPNet
- Focus结构
- Neck
- PANet
- 输出
- 目标损失函数
- IoU Loss
- GIoU Loss
- DIoU Loss
- CIoU Loss
- 总结
- DIOU_nms
- 参考
YOLO v4和v5版本在v3版本的基础上,组合了多种先进算法提升精度。为了能快速理解YOLO v4和v5,我们需要了解各种改进方法。此篇博文从输入端、主干网络、Neck和输出等四个方面简要介绍v4和v5中用到的改进方法。
输入端
Mosaic数据增强
数据增广:Mixup, Cutout 和 CutMix
Mosaic是一种数据增强方法,主要思想是将四张图片进行随机缩放、随机剪裁、随机排布的方式拼接到一张图上。CutMix数据增强方式是将两张图片进行拼接,然后将拼接好的图片送入到主干网络中。Mosaic则是将四张图片进行拼接。将拼接好的图片传入到主干网络当中去学习,相当于一下子传入了四张图片,极大地丰富了检测物体的背景,而且BN计算时,会计算四张图片的数据,使得batch size的不需要太大。

Self-Adversarial Training
自对抗训练(Self-adversarial training,SAT)是一种新的数据增强方式,分两个前后阶段进行操作。在第一阶段,神经网络改变原始图像而不是网络权重,通过这种方式,神经网络对自己进行对抗性攻击,改变原始图像,从而产生图像上没有所需物体的欺骗;在第二阶段,训练神经网络以正常的方式检测该修改图像上的物体。
CmBN

目前大部分流行的模型都会用到Batch Normalization,BN可以加快模型的收敛速度,在一定程度上缓解深层网络“梯度弥散”的问题。对一个batch,首先求出batch中所有特征图的均值和方差,然后对输入特征图进行归一化,将归一化的结果乘以尺度因子 γ \gamma γ,然后加上偏移量 β \beta β,得到最后输出。BN是在一个batch中计算所有均值和方差,当batch size越大时,均值和方差越接近整个训练集的均值和方差,所以一般训练时,需要将batch size尽可能设置大些。但是当batch size较小的时候,BN的效果会变差。
batch size太小,本质上还是数据量太少,不能近似整个数据集。CBN(Cross Batch Normalization)引入时间维度,通过计算前几个迭代计算好的均值和方差,一起计算本次迭代的均值和方差,通过这种方式变相扩大了batch size。前几个迭代的均值和方差由前几个迭代的网络参数计算得到的,在本轮迭代中计算BN时,前几轮迭代的参数已经过时了。CBN中引入泰勒公式解决上述问题。具体推导见论文。
CmBN是基于CBN改进的,CmBN是将大batch中的4个mini-batch看做一个整体,不需要前几个迭代时刻的BN参数。在大batch中的4个mini-batch中使用CBN进行计算。
主干网络
Mish激活函数
Mish激活函数是光滑的非单调激活函数,定义为: f ( x ) = x ⋅ t a n h ( l n ( 1 + e x ) ) f\left( x \right) = x \cdot tanh \left( ln \left( 1 + e^{x}\right) \right) f(x)=x⋅tanh(ln(1+ex)). 非单调这种性质有助于保持小的负值,从而稳定网络梯度流。

如上图所示,Mish函数无上界有下界。无上界属性是任何激活函数都需要的特性。有下界属性有助于实现强正则化效果。
DropBlock 正则化
DropBlock是一种针对卷积层的正则化方法,它是将整块的特征去除。如下图所示,(b)和(c)绿色区域中的激活单元包含输入图像的语义信息。因为临近的激活单元包含的语义信息比较接近,随机去除激活单元并不是有效的。相反,连续的区域包含特定的语义信息,去除连续的区域能够迫使剩余的单元学习可分类输入图像的特征信息。

下图是DropBlock的算法伪代码和图像示例。DropBlock并不应用在推理阶段,而是应用在训练阶段。DropBlock有两个超参数,block_size和 γ \gamma γ值的设定。 γ \gamma γ服从伯努利公式 γ = 1 − k e e p p r o b b l o c k s i z e 2 f e a t s i z e 2 ( f e a t s i z e − b l o c k s i z e + 1 ) 2 \gamma = \frac{1-keep_prob}{block_size^{2}} \frac{feat_size^{2}}{\left(feat_size - block_size + 1 \right)^{2}} γ=blocksize21−keepprob(featsize−blocksize+1)2featsize2。keep_prob固定值效果不好,需要一个线性衰减过程,从最初的1到设定的阈值。

CSPNet
跨阶段局部网络(Cross Stage Partial DenseNet, CSPNet)的设计目的是使网络架构能够实现更丰富的梯度组合,同时还减少计算量。CSPNet通过将基础层的特征图划分为两部分,然后通过跨阶段层次结构进行合并实现此目标。CSPNet论文作者的主要思想是:通过分割梯度流,使梯度流通过不同的网络路径传播。通过切换串联或者过渡步骤,传播的梯度信息可以具有较大的相关性差异。
下面两图分别是DenseNet和CSPDensNet单阶段架构图。DenseNet的每个单阶段包含一个Dense Block和一个Transition Layer。相比于DenseNet,CSPDenseNet将输入特征层 x 0 x_{0} x0在通道层面拆分成两部分, x 0 = [ x 0 ′ , x 0 ′ ′ ] x_{0} = [x_{0}', x_{0}''] x0=[x0′,x0′′],其中 x 0 ′ ′ x_{0}'' x0′′进入局部Dense Block,与在DenseNet中的操作一样; x 0 ′ x_{0}' x0′直接连接到阶段的末端。


假设每个Dense Block由 k k k个Dense Layer组成,下面表格列出了DenseNet和CSPDenseNet的前向计算和权重更新方程。在DenseNet中,大量的梯度信息被重用来更新不同Dense Layer的权重,这将导致无差异的Dense Layer反复学习同样的梯度信息。在CSPDenseNet中,Dense Layer的梯度是单独积分的。没有经过Dense Block的 x 0 ′ x_{0}' x0′也被单独积分。
| - | DenseNet | CSPDenseNet |
|---|---|---|
| 前向计算 |  |  |
| 权重更新 |  |  |
CSPNet可以很轻松地应用于ResNet和ResNeXt,如下图所示。由于只有一半地特征通道通过Res(X)Blocks,因此就不再需要引入bottleneck了。当固定FLOP时,这使理论上的内存访问成本(MAC)下限成为可能。

Focus结构
YOLO v5在图片进入主干网络前,对图片进行切片操作,执行切片操作的结构被称为Focus。Focus的具体操作是: 在一张大小为 h × w h \times w h×w的特征图中每隔一个像素取一个值组成新的特征图,那么就会得到四个大小为 h 2 × w 2 \frac{h}{2} \times \frac{w}{2} 2h×2w的特征图。假设原始的三通道图像大小为 640 × 640 × 3 640 \times 640 \times 3 640×640×3, 经过Focus结构之后,得到的特征图的大小为 320 × 320 × 12 320 \times 320 \times 12 320×320×12。

Swim-Transform中的patch merging layer层的操作和Focus结构很相似。
class Focus(nn.Module):# Focus wh information into c-spacedef __init__(self, c1, c2, k=1, s=1, p=None, g=1, act=True): # ch_in, ch_out, kernel, stride, padding, groupssuper(Focus, self).__init__()self.conv = Conv(c1 * 4, c2, k, s, p, g, act) # Focus后得到的特征图通道数扩了4倍def forward(self, x): # Focus操作特征图大小变化: x(b,c,w,h) -> y(b,4c,w/2,h/2)return self.conv(torch.cat([x[..., ::2, ::2], x[..., 1::2, ::2], x[..., ::2, 1::2], x[..., 1::2, 1::2]], 1))
Neck
目标检测领域,称主干网络和输出层之间的一些层为Neck。Yolov4和v5的Neck结构主要采用了SPP模块、FPN+PAN的方式。
PANet
下图是PANet被提出的网络结构图。(a)部分是FPN结构,FPN将高层得到的特征图进行上采样然后往下传递,为top-down的过程。高层特征图中包含丰富的语义信息,经过top-down的传播就可以使得这些语义信息传播到底层特征上,也让底层特征图包含丰富语义的信息。但是底层特征图却无法影响高层特征图。PANet引入了bottom-up的路径,让底层特征也传递到高层特征图中。
(a)(b)两个子图连在一起的过程就是:先进行up-bottom的特征融合之后,再进行bottom-up的特征融合。

如上图所示,采用ResNet作为基础架构,使用 { P 2 , P 3 , P 4 , P 5 } \{ P_{2}, P_{3}, P_{4}, P_{5}\} {P2,P3,P4,P5}为FPN的特征层,从 P 2 P_{2} P2到 P 5 P_{5} P5,特征图2倍下采样; { N 2 , N 3 , N 4 , N 5 } \{ N_{2}, N_{3}, N_{4}, N_{5}\} {N2,N3,N4,N5}是根据 { P 2 , P 3 , P 4 , P 5 } \{ P_{2}, P_{3}, P_{4}, P_{5}\} {P2,P3,P4,P5}新生成的特征层。 N i N_{i} Ni和 P i P_{i} Pi的特征图大小相同。
下图是up-bottom的局部块结构。 N i N_{i} Ni相比较于 N i + 1 N_{i+1} Ni+1为高分辨率特征图。首先需要将 N i N_{i} Ni通过一个步长为2的 3 × 3 3 \times 3 3×3的卷积减少特征图大小,得到新的特征图,然后新特征图中的元素和 P i + 1 P_{i+1} Pi+1中的元素相加得到融合特征图,融合特征图再经过一个 3 × 3 3 \times 3 3×3的卷积生成 N i + 1 N_{i+1} Ni+1。

输出
目标损失函数
目标检测的损失函数一般由分类损失函数和回归损失函数组成。近些年来,回归损失函数从直接回归bbox的4个坐标点,逐渐将bbox作为一个整体进行回归。回归损失函数的发展历程如下所示:
L1 loss–> L2 loss–> Smooth L1 Loss–>IoU Loss -->GIoU Loss --> DIoU loss --> CIoU Loss
Smooth L1 损失函数是分段函数,综合了L1 和L2的优点,在x较大时( ∣ x ∣ ≥ 1 |x| \geq 1 ∣x∣≥1),为L1 损失函数,L1损失函数的导数为常数,保证模型训练前期有稳定的梯度。在x比较小时 ∣ x ∣ < 1 |x|<1 ∣x∣<1,为L2损失函数,L2处处可导,在0值周围具有较小的梯度,波动小更加稳定。
L1,L2和Smooth L1 Loss都是独立地计算4个点的Loss,这种做法默认这4个点是相互独立的,没有考虑bbox四个坐标之间的相关性。
IoU Loss
交并比IoU(Intersection over Union),计算预测框和真实框的交集和并集的比值。假设预测框为 A A A,真实框为 B B B,那么交并比的公式定义为: IoU = A ∩ B A ∪ B \frac{A \cap B}{A \cup B} A∪BA∩B
16年论文UnitBox: An Advanced Object Detection Network中提出了IoU Loss将bbox作为一个整体做回归。
IoU Loss的定义是先求出预测框与真实框之间的交并比之后,再求负对数。用公式简要表示就是: I o U l o s s = − l n ( I o U ( b b o x g t , b b o x p r e d ) ) IoUloss = -ln \left( IoU(bbox_{gt}, bbox_{pred}) \right) IoUloss=−ln(IoU(bboxgt,bboxpred))。IoU满足非负性、统一性、对称性、三角不等性,而且相比于距离损失函数还具有尺度不变性,不论bbox的大小,IoU loss的取值位于 ( 0 , 1 ) (0,1) (0,1)。

但是当预测框和真实框不相交时,也就是 I o U ( b b o x g t , b b o x p r e d ) = 0 IoU(bbox_{gt}, bbox_{pred})=0 IoU(bboxgt,bboxpred)=0,IoU loss为0,损失函数在0处不可导,没有梯度回传,无法进行学习训练。
GIoU Loss
GIoU(Generalized Intersection over Union)引入了预测框 A A A和真实框 B B B的最小外接矩形 C C C。 G I o U = I o U − C ∖ ( A ∪ B ) ∣ C ∣ GIoU = IoU - \frac{C \setminus \left(A \cup B \right)}{|C|} GIoU=IoU−∣C∣C∖(A∪B)。GIoU不仅可以关注重叠区域,还可关注非重合区域,能比较好地反应预测框和真实框在闭包区域的相交情况。

如下所示,绿色框为真实框,红色框为预测框。GIoU中加入了预测框和真实框得最小外接矩形,但是当真实框包含预测框时, C ∖ ( A ∪ B ) ∣ C ∣ = 0 \frac{C \setminus \left(A \cup B \right)}{|C|}=0 ∣C∣C∖(A∪B)=0,GIoU就退化为IoU,无法确定真实框和预测框之间的相对关系。

DIoU Loss
由于GIoU过度依赖IoU项,尤其对水平和垂直bbox,GIoU需要更多迭代步数收敛。DIoU仅在IoU 的基础上添加一个惩罚项,直接最小化两个bbox中心点之间的归一化距离(normalized distance),这样也能比GIoU更快地收敛。

假设预测框为 B B B,真实框为 B g t B^{gt} Bgt。
D I o U = I o U − ρ 2 ( b , b g t ) c 2 DIoU = IoU - \frac{\rho^{2} \left( b, b^{gt} \right)}{c^{2}} DIoU=IoU−c2ρ2(b,bgt)
其中 b b b和 b g t b^{gt} bgt是预测框 B B B和真实框 B g t B^{gt} Bgt的中心点, ρ ( ⋅ ) \rho\left( \cdot \right) ρ(⋅)是欧式距离,如上图所示,红色的线段为两个框中心点之间的距离 d = ρ ( b , b g t ) d=\rho \left( b, b^{gt} \right) d=ρ(b,bgt), c c c是覆盖两个检测框的最小矩形的对角线长度。如上图所示,灰色那么DIoU loss函数被定义如下:
L D I o U = 1 − I o U + ρ 2 ( b , b g t ) c 2 L_{DIoU} = 1 - IoU + \frac{\rho^{2} \left( b, b^{gt} \right)}{c^{2}} LDIoU=1−IoU+c2ρ2(b,bgt)
CIoU Loss
一个好的bbox回归损失函数应当包含三个重要的几何因素:重合区域、中心点距离和纵横比。IoU考虑到了重合区域,GIoU高度依赖IoU,DIoU同时考虑了重合区域和中心点距离。然而,bbox的纵横比的一致性仍然是一项重要的几何因素。因此,基于DIoU,CIoU中添加了bbox的纵横比,CIoU的公式定义如下:
C I o U = I o U − ρ 2 ( b , b g t ) c 2 − α u CIoU = IoU - \frac{\rho^{2} \left( b, b^{gt} \right)}{c^{2}} - \alpha u CIoU=IoU−c2ρ2(b,bgt)−αu
其中 α \alpha α是正超参数, u u u计算纵横比的一致性。 α \alpha α和 u u u的公式定义如下:
u = 4 π 2 ( a r c t a n w g t h g t − a r c t a n w h ) 2 u = \frac{4}{\pi^{2}}\left( arctan \frac{w^{gt}}{h^{gt}} - arctan \frac{w}{h}\right)^{2} u=π24(arctanhgtwgt−arctanhw)2
α = u ( 1 − I o U ) + u \alpha = \frac{u}{\left(1 - IoU \right) + u } α=(1−IoU)+uu
CIoU 损失函数的定义如下所示:
L C I o U = 1 − I o U + ρ 2 ( b , b g t ) c 2 + α u L_{CIoU} = 1 - IoU + \frac{\rho^{2} \left( b, b^{gt} \right)}{c^{2}} + \alpha u LCIoU=1−IoU+c2ρ2(b,bgt)+αu
总结
| 方法 | 优点 | 缺点 |
|---|---|---|
| IoU | IoU具有尺度不变性;IoU的结果范围为(0,1),非负 | 如果两个框不相交,IoU将为0,无法反映两个框的距离远近;IoU无法精确地反映两个框的重合度大小。 |
| GIoU | 引入两个框的最小外接矩形,解决两个框没有交集时梯度为零的问题;GIoU不仅关注重叠区域,还关注非重合区域,能比较好地反映两个框在闭包区域的相交情况 | 当两个框属于包含关系时,GIoU会退化成IoU。 |
| DIoU | DIoU考虑到了两个框之间的距离,重叠率和尺度,使得回归变得更加稳定 | DIoU没考虑bbox的纵横比 |
| CIoU | 在DIoU的基础上,加入了纵横比 | 纵横比描述的是相对值 |
DIOU_nms
我们先回忆一下NMS算法的具体步骤。首先按照候选框的得分对所有的候选框进行排序;选择分数最大的候选框M,将其他与M的IoU值超过阈值的框剔除;迭代这一过程直到所有的框被检测完成。在原始的NMS中,IoU用来抑制多余的检测框,重叠区域是唯一的因素,会导致两个相近物体的检测框被错误地剔除。
DIoU不仅仅考虑到了重叠区域,还考虑到两个框的中心点距离。DIoU替代IoU可作为NMS中一个较好的标准。DIoU NMS假设两个远距离的候选框中是不同的物体。对一个具有最高分数的预测框M来说,DIoU可以公式化地定义如下:
s i = { s i , I o U − R D I o U ( M , B i ) < ε 0 , I o U − R D I o U ( M , B i ) ≥ ε s_{i} = \left\{\begin{matrix} s_{i},& IoU - R_{DIoU}\left ( M,B_{i} \right ) < \varepsilon \\ 0 ,& IoU - R_{DIoU}\left ( M,B_{i} \right ) \ge \varepsilon \end{matrix}\right. si={si,0,IoU−RDIoU(M,Bi)<εIoU−RDIoU(M,Bi)≥ε
如上述公式所示,候选框 B i B_{i} Bi被移除需要同时考虑IoU和两个框中心点之间的距离两个因素。 s i s_{i} si是分类分数, ε \varepsilon ε是NMS阈值。
参考
- AlexeyAB/darknet
- UnitBox: An Advanced Object Detection Network
- Generalized Intersection over Union: A Metric and A Loss for Bounding Box Regression
- Distance-IoU Loss: Faster and Better Learning for Bounding Box Regression
- CSPNET: A NEW BACKBONE THAT CAN ENHANCE LEARNING
CAPABILITY OF CNN - DropBlock: A regularization method for convolutional networks
- Path Aggregation Network for Instance Segmentation
- Tianxiaomo/pytorch-YOLOv4
相关文章:

【YOLO 系列】YOLO v4-v5先验知识
文章目录 输入端Mosaic数据增强Self-Adversarial TrainingCmBN 主干网络Mish激活函数DropBlock 正则化CSPNetFocus结构 NeckPANet 输出目标损失函数IoU LossGIoU LossDIoU LossCIoU Loss总结 DIOU_nms 参考 YOLO v4和v5版本在v3版本的基础上,组合了多种先进算法提升…...

4年外包终于上岸,我只能说别去....
我大学学的是计算机专业,毕业的时候,对于找工作比较迷茫,也不知道当时怎么想的,一头就扎进了一家外包公司,一干就是4年。现在终于跳槽到了互联网公司了,我想说的是,但凡有点机会,千万…...
Nginx快速入门
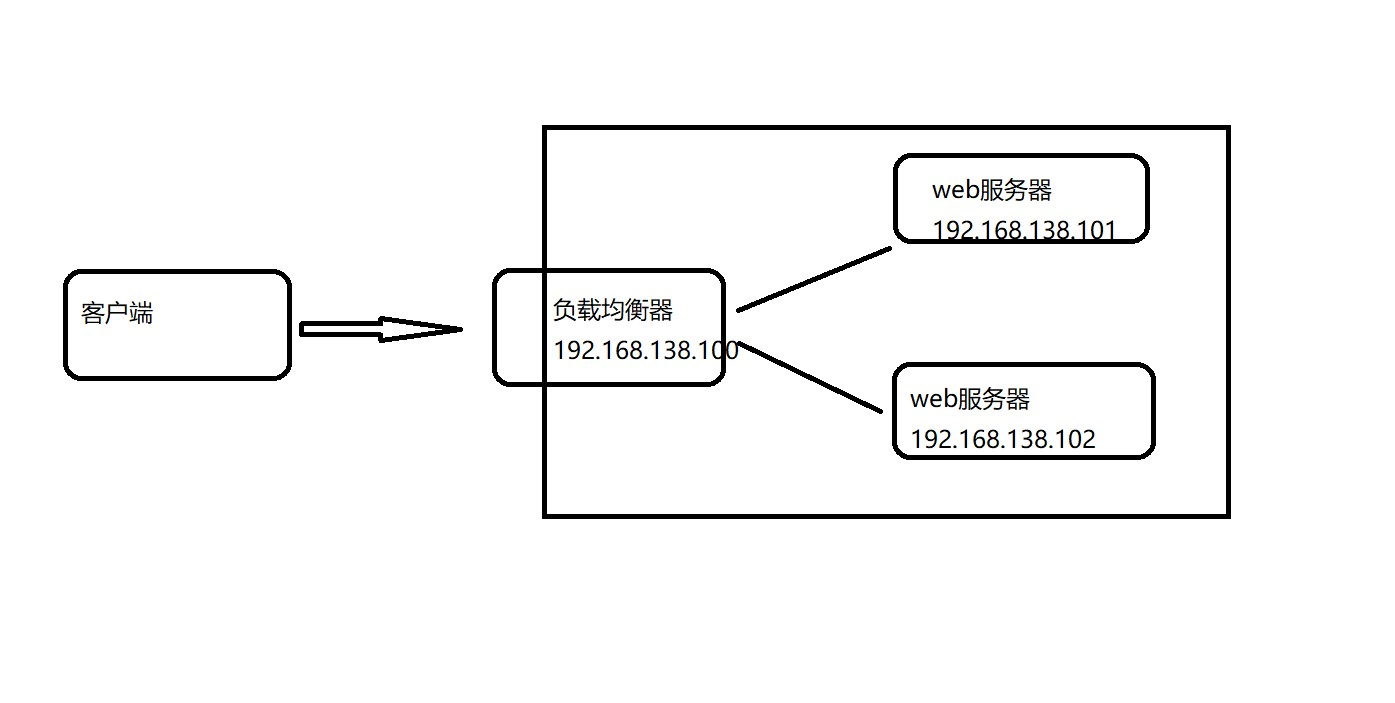
1.nginx概述 nginx介绍 nginx是一款轻量级的web服务器/方向代理服务器及电子邮件(IMAP/POP3)代理服务器。其特点是占有内存少,并发能力强,事实上nginx的并发能力在同类型的网页服务器中表现较好,中国大陆使用nginx的网…...
Leetcode507. 完美数
Every day a leetcode 题目来源:507. 完美数 解法1:枚举 我们可以枚举 num 的所有真因子,累加所有真因子之和,记作 sum。若 sumnum 则返回 true,否则返回 false。 枚举范围从 [1, sum) 的话,会超时&…...
 std::vector (九))
c++ 11标准模板(STL) std::vector (九)
定义于头文件 <vector> template< class T, class Allocator std::allocator<T> > class vector;(1)namespace pmr { template <class T> using vector std::vector<T, std::pmr::polymorphic_allocator<T>>; }(2)(C17…...

从Facebook到Diem币:社交媒体巨头在加密货币领域的演变
大家都知道Facebook是一个全球知名的社交媒体平台,几乎每个人都在其中与朋友分享照片、发表状态或留言。 然而,随着时间的推移,Facebook不仅仅局限于社交交流,而是逐渐涉足更广阔的领域,其中之一就是加密货币。在本文…...

利用font-spider对CSS字体进行压缩
ont-spider利器是一款强大的字体压缩工具,可以将网页中的字体压缩到最小,从而节省网络带宽和提高页面加载速度。在实际使用中,font-spider利器对webfont网页字体压缩使用可以让网页字体更加清晰,用户体验更好。 一、font-spider利…...

2023年软考系统架构师新版专栏导读
目录 新的改变软考是不是内卷?老版教材删减章节建议学习计划专栏更文列表 新的改变 软考今年改版啦 高级系统架构师考试在2022年12月底出了第二版教材,比第二版多出来140页,虽然看起来好像更难了,但是我认为改版是件好事…...
)
时间表体验(2023.05.05-2023.05.06)
2023.05.05 2023.05.04青年节后第一天,然而我的公司并没有在五四下午放假,吐槽一下腾讯IEG。 大晚上出租屋的床塌了,我靠,倒霉,不过还好不要我出钱去修,120斤重的我怎么可能把床压踏呢?&#…...

linux系统查询二进制BIn文件方法
在 Linux 上分析二进制文件的方法有很多,以下是其中几种常见的方法: 使用 objdump 命令 objdump 命令可以显示二进制文件的汇编代码、符号表和其他信息,可以用来分析二进制文件的结构和代码逻辑。例如: objdump -d binaryfile这…...
)
api接口调用(1688/Taobao/jd平台API接口的调用实例)
api接口调用 CURL 是一个利用URL语法规定来传输文件和数据的工具,支持很多协议,如HTTP、FTP、TELNET等。最爽的是,PHP也支持 CURL 库。使用PHP的CURL 库可以简单和有效地去抓网页。你只需要运行一个脚本,然后分析一下你所抓取的网…...

Python+Yolov5舰船侦测识别
程序示例精选 PythonYolov5舰船侦测识别 如需安装运行环境或远程调试,见文章底部个人QQ名片,由专业技术人员远程协助! 前言 这篇博客针对<<PythonYolov5舰船侦测识别>>编写代码,代码整洁,规则,…...

Qt5.9学习笔记-事件(五) 事件调试和排查
⭐️我叫忆_恒心,一名喜欢书写博客的在读研究生👨🎓。 如果觉得本文能帮到您,麻烦点个赞👍呗! 近期会不断在专栏里进行更新讲解博客~~~ 有什么问题的小伙伴 欢迎留言提问欧,喜欢的小伙伴给个三…...

【实用工具】SpringBoot实现接口签名验证
需求场景 由于项目需要开发第三方接口给多个供应商,为保证Api接口的安全性,遂采用Api接口签名验证。 Api接口签名验证主要防御措施为以下几个: 请求发起时间得在限制范围内请求的用户是否真实存在是否存在重复请求请求参数是否被篡改 项目…...

DDR基础
欢迎关注我的博客网站nr-linux.com,图片清晰度和,排版会更好些,文章优先更新至博客站。 DDR全称Double Data Rate Synchronous Dynamic Random Access Memory,是当代处理器必不可少的存储器件之一。本文关于DDR介绍的核心点如下&…...

理解find命令
find命令使用通配符,而不是正则表达式 对于如下两个命令 find ./ -name *txt 和 find ./ -name \*txt 这两个命令之间的区别在于 shell 对通配符字符 * 的解释和展开方式不同。 find ./ -name *txt:在这个命令中,shell 在将命令传递给 fin…...

OpenCV教程——调整图像亮度与对比度,绘制形状和文字
调整图像亮度与对比度 1.图像变换 图像变换通常有两种方式: 像素变换:点操作邻域操作:区域 调整图像亮度和对比度属于像素变换(点操作)。 2.调整图像亮度与对比度 可以通过以下公式调整图像的亮度和对比度&#…...

Python模块篇:函数/类/变量和常量/注释/导入和使用
大家好,我是辣条哥!本期应邀写了一些Python模块相关内容~ Python模块是一种组织Python代码的方式,它将相关的代码放在一个文件中,以便于重用和维护。Python模块可以包含函数、类、变量和常量等,可以被其他Python程序导…...

Java反射和动态代理
反射 反射允许对封装类的成员变量、成员方法和构造方法的信息进行编程访问 成员变量:修饰符、名字、类型、get/set值 构造方法:修饰符、名字、形参、创建对象 成员方法:修饰符、名字、形参、返回值、抛出的异常、获取注解、运行方法 获取…...
Python实现)
[NOIP2004 提高组] 津津的储蓄计划(思路+代码详解)Python实现
题目描述 津津的零花钱一直都是自己管理。每个月的月初妈妈给津津300 元钱,津津会预算这个月的花销,并且总能做到实际花销和预算的相同。 为了让津津学习如何储蓄,妈妈提出,津津可以随时把整百的钱存在她那里,到了年…...

利用ngx_stream_return_module构建简易 TCP/UDP 响应网关
一、模块概述 ngx_stream_return_module 提供了一个极简的指令: return <value>;在收到客户端连接后,立即将 <value> 写回并关闭连接。<value> 支持内嵌文本和内置变量(如 $time_iso8601、$remote_addr 等)&a…...

R语言AI模型部署方案:精准离线运行详解
R语言AI模型部署方案:精准离线运行详解 一、项目概述 本文将构建一个完整的R语言AI部署解决方案,实现鸢尾花分类模型的训练、保存、离线部署和预测功能。核心特点: 100%离线运行能力自包含环境依赖生产级错误处理跨平台兼容性模型版本管理# 文件结构说明 Iris_AI_Deployme…...

【力扣数据库知识手册笔记】索引
索引 索引的优缺点 优点1. 通过创建唯一性索引,可以保证数据库表中每一行数据的唯一性。2. 可以加快数据的检索速度(创建索引的主要原因)。3. 可以加速表和表之间的连接,实现数据的参考完整性。4. 可以在查询过程中,…...

Nginx server_name 配置说明
Nginx 是一个高性能的反向代理和负载均衡服务器,其核心配置之一是 server 块中的 server_name 指令。server_name 决定了 Nginx 如何根据客户端请求的 Host 头匹配对应的虚拟主机(Virtual Host)。 1. 简介 Nginx 使用 server_name 指令来确定…...

多种风格导航菜单 HTML 实现(附源码)
下面我将为您展示 6 种不同风格的导航菜单实现,每种都包含完整 HTML、CSS 和 JavaScript 代码。 1. 简约水平导航栏 <!DOCTYPE html> <html lang"zh-CN"> <head><meta charset"UTF-8"><meta name"viewport&qu…...

C++八股 —— 单例模式
文章目录 1. 基本概念2. 设计要点3. 实现方式4. 详解懒汉模式 1. 基本概念 线程安全(Thread Safety) 线程安全是指在多线程环境下,某个函数、类或代码片段能够被多个线程同时调用时,仍能保证数据的一致性和逻辑的正确性…...

tree 树组件大数据卡顿问题优化
问题背景 项目中有用到树组件用来做文件目录,但是由于这个树组件的节点越来越多,导致页面在滚动这个树组件的时候浏览器就很容易卡死。这种问题基本上都是因为dom节点太多,导致的浏览器卡顿,这里很明显就需要用到虚拟列表的技术&…...

初探Service服务发现机制
1.Service简介 Service是将运行在一组Pod上的应用程序发布为网络服务的抽象方法。 主要功能:服务发现和负载均衡。 Service类型的包括ClusterIP类型、NodePort类型、LoadBalancer类型、ExternalName类型 2.Endpoints简介 Endpoints是一种Kubernetes资源…...

JavaScript 数据类型详解
JavaScript 数据类型详解 JavaScript 数据类型分为 原始类型(Primitive) 和 对象类型(Object) 两大类,共 8 种(ES11): 一、原始类型(7种) 1. undefined 定…...

Java中栈的多种实现类详解
Java中栈的多种实现类详解:Stack、LinkedList与ArrayDeque全方位对比 前言一、Stack类——Java最早的栈实现1.1 Stack类简介1.2 常用方法1.3 优缺点分析 二、LinkedList类——灵活的双端链表2.1 LinkedList类简介2.2 常用方法2.3 优缺点分析 三、ArrayDeque类——高…...
