D1. LuoTianyi and the Floating Islands (Easy Version)(树形dp)
Problem - D1 - Codeforces

这是问题的简化版本。唯一的区别在于在该版本中k≤min(n,3)。只有在两个版本的问题都解决后,才能进行黑客攻击。 琴音和漂浮的岛屿。
洛天依现在生活在一个有n个漂浮岛屿的世界里。这些漂浮岛屿由n−1个无向航线连接,任意两个岛屿之间都可以通过这些航线到达。也就是说,这n个漂浮岛屿形成了一棵树。
有一天,洛天依想见她的朋友:Chtholly、Nephren、William等。她总共想见k个人。她不知道他们的确切位置,但是她知道他们在两两不同的岛屿上。她定义一个岛屿是好的,当且仅当从它到具有k个人的岛屿的距离和为所有n个岛屿中最小的时候。
现在,洛天依想知道,如果将k个人随机放置在n个岛屿中的k个不同的岛屿上,那么好的岛屿的期望数量是多少?你只需要告诉她期望数量模109+7的值。
†
两个岛屿之间的距离是你需要采取的最少的航线数量,以到达另一个岛屿。 输入
第一行包含两个整数n和k(1≤k≤min(n,3),1≤n≤2⋅105) - 岛屿和人的数量。
接下来的n−1行描述了航线。它们中的第i行包含两个整数ui和vi(1≤ui,vi≤n,ui≠vi)-第i条空中路线连接的岛屿。 输出
打印一个整数-好岛屿的期望数字模109+7。
严格地说,让M=109+7。可以证明答案可以表示为不可约分数pq,其中p和q是整数,q≢0(modM)。输出等于p⋅q−1modM的整数。换句话说,输出这样一个整数x,使得0≤x<M且x⋅q≡p(modM)。
Examples
Input
Copy
4 2 1 2 2 3 3 4
Output
Copy
666666674
Input
Copy
5 1 1 2 2 3 3 4 3 5
Output
Copy
1
题解:
对于k = 1的情况,无论这个点在哪,唯一的好点就是其本身,只有一种可能,所以直接输出1
对于k = 3的情况,我们可以先确定一个中间的点,这个点肯定不能在叶子节点上,另外两个点分别放在这个中点两边,我们会发现这样好点只会是中点本身,也输出1
对于k = 2的情况,我们可以发现,这两人在任何两个不同的点上,好点的数量是两个点相连链上的点的数目,我们可以通过单个点对答案的贡献来求
我们在dfs时可以求所有点的子树大小,对于这些点对答案的贡献为,
dp[ne]*(n - dp[ne]),可以理解为右节点在子树中,左节点在子树外,
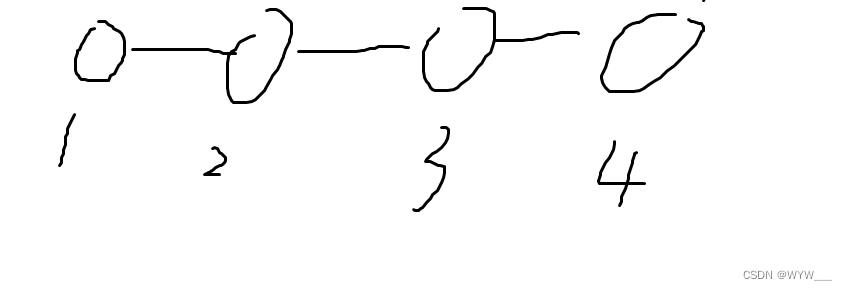
这样计算完,我们得到的好点数是10,而答案是16,显然少了一些贡献,我们多举几个例子就能发现,还要加上n*(n - 1)/2,(至于为啥是这样,想了好长时间,实在想不明白,望大佬帮忙指正)
最后别忘了除概率n*(n - 1)/2,
#include <cstdio>
#include <cstring>
#include <algorithm>
#include<iostream>
#include<vector>
#include<set>
#include<map>
#include<cmath>
#include<queue>
using namespace std;
typedef long long ll;
#define int long long
typedef pair<int,int> PII;
const int N = 3e5 + 10;
int mod = 1e9 + 7;
vector<int> p[300050];
int ans;
int qpow(int x,int y)
{int ans = 1;while(y){if(y&1)ans = ans*x%mod;x = x*x%mod;y /= 2;} return ans;
}
int m,n;
int dp[N];
void dfs(int x,int fa)
{dp[x] = 1;for(auto ne:p[x]){if(ne == fa)continue;dfs(ne,x);dp[x] = dp[x] + dp[ne];ans = (ans + dp[ne]*(n - dp[ne])%mod)%mod;
// cout <<ne <<" "<<dp[ne] <<"\n";}
}
void solve()
{int k;cin >> n >> k;for(int i = 1;i < n;i++){int x,y;cin >> x >> y;p[x].push_back(y);p[y].push_back(x);}if(k == 1||k == 3){cout << 1;}else if(k == 2){m = qpow((n*(n - 1)/2)%mod,mod - 2);dfs(1,0);
// cout << ans ;cout << (ans + (n*(n - 1)/2)%mod)%mod*m%mod;}
}
signed main()
{ios::sync_with_stdio(0 );cin.tie(0);cout.tie(0);int t = 1;
// cin >> t;while(t--){solve(); }
}
相关文章:
D1. LuoTianyi and the Floating Islands (Easy Version)(树形dp)
Problem - D1 - Codeforces 这是问题的简化版本。唯一的区别在于在该版本中k≤min(n,3)。只有在两个版本的问题都解决后,才能进行黑客攻击。 琴音和漂浮的岛屿。 洛天依现在生活在一个有n个漂浮岛屿的世界里。这些漂浮岛屿由n−1个无向航线连接,任意两个…...

rk3588移植ubuntu server
ubuntu server 18.04 arm版本. 1、使用qemu运行 安装qemu-system-aarch64 sudo apt install -y qemu-system-arm 2、下载ubuntu server Index of /releases/18.04.3 3、创建虚拟磁盘 qemu-img create ubuntuimg.img 40G 4、创建虚拟机 弹出界面,直接回车选…...

如何更好地刷力扣
之前刷力扣是一口气看很多题目,打算时不时看一会题解,逐渐熟悉套路,争取背过,最后就可以写出来了。我个人是背知识比较喜欢这种方法,但后来发现根本不适用 算法题本身就比较复杂,不经过实际写代码中的思考…...

上采样和下采样
首先,谈谈不平衡数据集。不平衡数据集指的是训练数据中不同类别的样本数量差别较大的情况。在这种情况下,模型容易出现偏差,导致模型对数量较少的类别预测效果不佳。 为了解决这个问题,可以使用上采样和下采样等方法来调整数据集…...

小猪,信息论与我们的生活
前言 动态规划是大家都熟悉与陌生的知识,非常灵活多变,我自己也不敢说自己掌握了,今天给大家介绍一道题,不仅局限于动态规划做题,还会上升到信息论,乃至于启发自己认知世界的角度 因为比较难,本…...
【鸿蒙应用ArkTS开发系列】- http网络库使用讲解和封装
目录 前言http网络库组件介绍http网络库封装创建Har Module创建RequestOption 配置类创建HttpCore核心类创建HttpManager核心类对外组件导出添加网络权限 http网络库依赖和使用依赖http网络库(httpLibrary)使用http网络库(httpLibrary&#x…...

【Java零基础入门篇】第 ⑥ 期 - 异常处理
博主:命运之光 专栏:Java零基础入门 学习目标 掌握异常的概念,Java中的常见异常类; 掌握Java中如何捕获和处理异常; 掌握自定义异常类及其使用; 目录 异常概述 异常体系 常见的异常 Java的异常处理机制…...

计算职工工资
目录 问题描述 程序设计 问题描述 【问题描述】 给定N个职员的信息,包括姓名、基本工资、浮动工资和支出,要求编写程序顺序输出每位职员的姓名和实发工资(实发工资=基本工资+浮动工资-支出)。 【输入形式】 输入在一行中给出正整数N。随后N行,每行给出一位职员的信息,…...

2019年上半年软件设计师下午试题
试题四(共 15 分) 阅读下列说明和 C 代码,回答问题 1 至 3,将解答写在答题纸的对应栏内 【说明】 n 皇后问题描述为:在一个 n*n 的棋盘上摆放 n 个皇后,要求任意两个皇后不能冲突, 即任意两个皇后不在同一行、同一列或者同一斜…...

IS200TPROH1BCB用于工业应用和电力分配等。高压型隔离开关用于变电站
IS200TPROH1BCB用于工业应用和电力分配等。高压型隔离开关用于变电站 什么是隔离器,它与断路器有何不同 什么是隔离器,为什么要使用隔离器 隔离器是一种开关装置,它可以手动或自动操作,隔离一部分电能。隔离器可用于在无负载情…...
【MySql】数据库 select 进阶
数据库 数据库表的设计ER 关系图三大范式 聚合函数与分组查询聚合函数 (count、sum、avg、max、min)分组查询 group by fields....having....(条件) 多表联查内连接外连接(左连接,右连接)自连接子查询合并查询 UNION 数据库表的设计 ER 关系…...

CVPR 2023 | VoxelNeXt实现全稀疏3D检测跟踪,还能结合Seg Anything
在本文中,研究者提出了一个完全稀疏且以体素为基础的3D物体检测和跟踪框架VoxelNeXt。它采用简单的技术,运行快速,没有太多额外的成本,并且可以在没有NMS后处理的情况下以优雅的方式工作。VoxelNeXt在大规模数据集nuScenes、Waymo…...
本地使用3台centos7虚拟机搭建K8S集群教程
第一步 准备3台centos7虚拟机 3台虚拟机与主机的网络模式都是桥接的模式,也就是他们都是一台独立的“主机” (1)kebe-master的配置 虚拟机配置: 网络配置: (2)kebe-node1的配置 虚拟机配…...

NVIDIA CUDA驱动安装
1 引言 因为笔记本电脑上运行Milvus图像检索代码,需要安装CUDA驱动。电脑显卡型号是NVIDIA GeForce GTX 1050 Ti Mobile, 操作系统是Ubuntu 20.04,内核版本为Linux 5.15.0-72-generic。 2 CUDA驱动测试 参考网上的资料:https://blog.csdn.…...

python 从excel中获取需要执行的用例
classmethod def get_excel_data(cls, excel_name, sheet_name, case_numNone):"""读取excel文件的方法:param excel_name: 文件名称:param sheet_name: sheet页的名称:param case_name: 执行的case名称:return:"""def get_row_data(table, row)…...

Web3中文|乱花渐欲meme人眼,BRC-20总市值逼近10亿美元
现在的Web3加密市场,用“乱花渐欲meme人眼”来形容再合适不过了。 何为meme? “meme”这个词大概很多人都不知道如何正确发音,并且一看到它就会和狗狗币Dogecoin等联系在一起。那它究竟从何而来呢? Meme:[mi:m]&#x…...

盖雅案例入选「首届人力资源服务国际贸易交流合作大会20项创新经验」
近日,首届人力资源服务国际贸易交流合作大会顺利召开。为激励企业在人力资源服务贸易领域不断创新,加快培育对外贸易新业态、新模式,形成人力资源服务领域国际竞争新优势,大会评选出了「首届人力资源服务国际贸易交流合作大会20项…...

[论文笔记]SimMIM:a Simple Framework for Masked Image Modeling
文章地址:https://arxiv.org/abs/2111.09886 代码地址:https://github.com/microsoft/SimMIM 文章目录 摘要文章思路创新点文章框架Masking strategyPrediction headPrediction targetEvaluation protocols 性能实验实验设置Mask 策略预测头目标分辨率预…...
----索引/视图/范式)
mysql从零开始(4)----索引/视图/范式
接上文 mysql从零开始(3) 索引 索引是在数据库表的字段上添加的,是为了提高查询效率存在的一种机制。一张表的一个字段可以添加一个索引,也可以多个字段联合起来添加索引。索引相当于一本书的目录,是为了缩小扫描范围…...
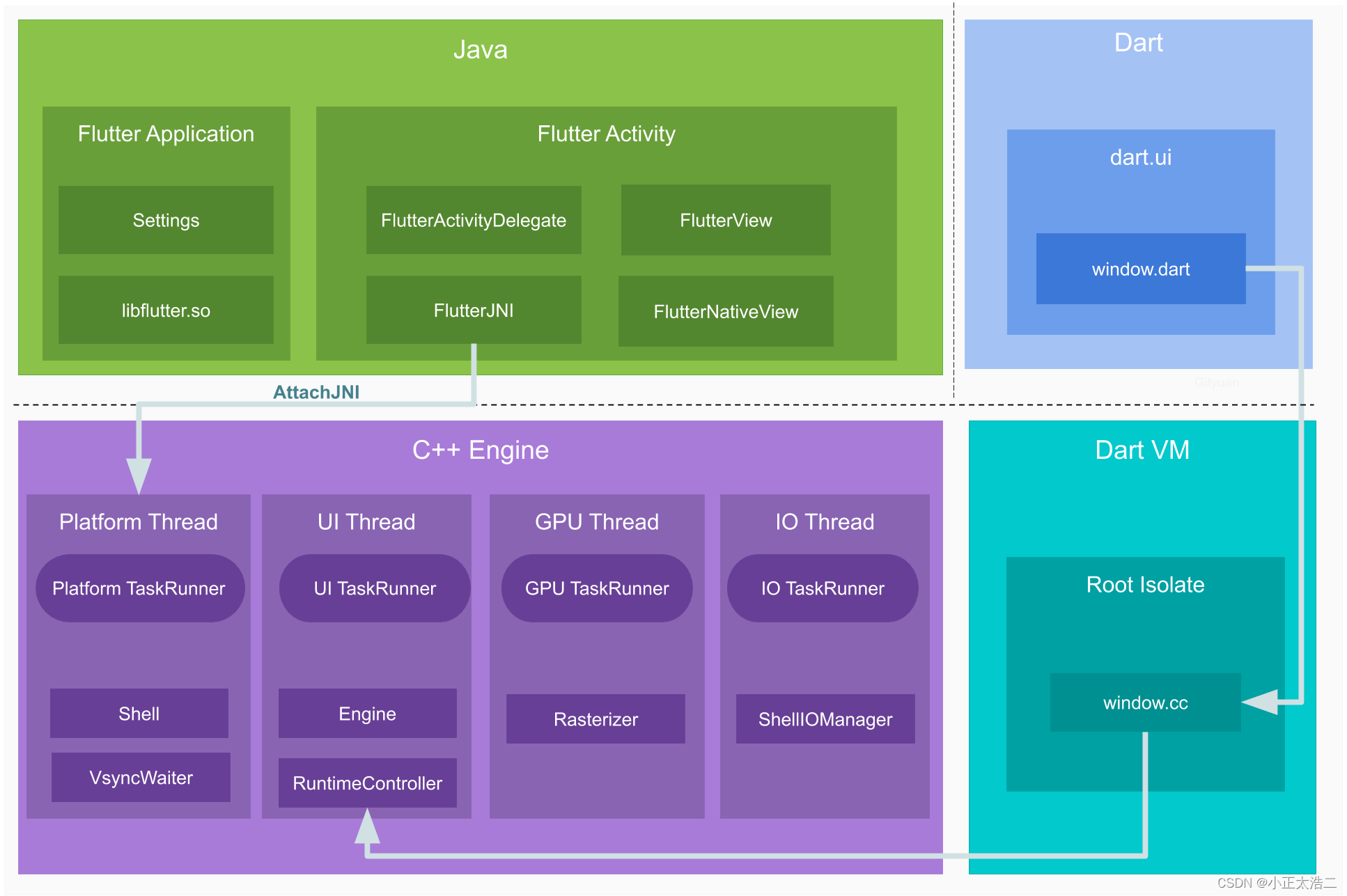
Flutter框架:从入门到实战,构建跨平台移动应用的全流程解析
第一章:Flutter框架介绍 Flutter框架是由Google推出的一款跨平台移动应用开发框架。相比其他跨平台框架,Flutter具有更高的性能和更好的用户体验。本章将介绍Flutter框架的概念、特点以及与其他跨平台框架的比较,以及Flutter开发环境的搭建和…...

Vim 调用外部命令学习笔记
Vim 外部命令集成完全指南 文章目录 Vim 外部命令集成完全指南核心概念理解命令语法解析语法对比 常用外部命令详解文本排序与去重文本筛选与搜索高级 grep 搜索技巧文本替换与编辑字符处理高级文本处理编程语言处理其他实用命令 范围操作示例指定行范围处理复合命令示例 实用技…...

AI-调查研究-01-正念冥想有用吗?对健康的影响及科学指南
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

《Qt C++ 与 OpenCV:解锁视频播放程序设计的奥秘》
引言:探索视频播放程序设计之旅 在当今数字化时代,多媒体应用已渗透到我们生活的方方面面,从日常的视频娱乐到专业的视频监控、视频会议系统,视频播放程序作为多媒体应用的核心组成部分,扮演着至关重要的角色。无论是在个人电脑、移动设备还是智能电视等平台上,用户都期望…...

Qt Widget类解析与代码注释
#include "widget.h" #include "ui_widget.h"Widget::Widget(QWidget *parent): QWidget(parent), ui(new Ui::Widget) {ui->setupUi(this); }Widget::~Widget() {delete ui; }//解释这串代码,写上注释 当然可以!这段代码是 Qt …...

Vue2 第一节_Vue2上手_插值表达式{{}}_访问数据和修改数据_Vue开发者工具
文章目录 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染2. 插值表达式{{}}3. 访问数据和修改数据4. vue响应式5. Vue开发者工具--方便调试 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染 准备容器引包创建Vue实例 new Vue()指定配置项 ->渲染数据 准备一个容器,例如: …...

【2025年】解决Burpsuite抓不到https包的问题
环境:windows11 burpsuite:2025.5 在抓取https网站时,burpsuite抓取不到https数据包,只显示: 解决该问题只需如下三个步骤: 1、浏览器中访问 http://burp 2、下载 CA certificate 证书 3、在设置--隐私与安全--…...

【Web 进阶篇】优雅的接口设计:统一响应、全局异常处理与参数校验
系列回顾: 在上一篇中,我们成功地为应用集成了数据库,并使用 Spring Data JPA 实现了基本的 CRUD API。我们的应用现在能“记忆”数据了!但是,如果你仔细审视那些 API,会发现它们还很“粗糙”:有…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个生活电费的缴纳和查询小程序
一、项目初始化与配置 1. 创建项目 ohpm init harmony/utility-payment-app 2. 配置权限 // module.json5 {"requestPermissions": [{"name": "ohos.permission.INTERNET"},{"name": "ohos.permission.GET_NETWORK_INFO"…...

爬虫基础学习day2
# 爬虫设计领域 工商:企查查、天眼查短视频:抖音、快手、西瓜 ---> 飞瓜电商:京东、淘宝、聚美优品、亚马逊 ---> 分析店铺经营决策标题、排名航空:抓取所有航空公司价格 ---> 去哪儿自媒体:采集自媒体数据进…...

智能AI电话机器人系统的识别能力现状与发展水平
一、引言 随着人工智能技术的飞速发展,AI电话机器人系统已经从简单的自动应答工具演变为具备复杂交互能力的智能助手。这类系统结合了语音识别、自然语言处理、情感计算和机器学习等多项前沿技术,在客户服务、营销推广、信息查询等领域发挥着越来越重要…...
