David Silver Lecture 5: Model-Free Control
1 Introduction
1.1 内容
上一章是对一个unknown MDP进行value function的预测,相当于policy evaluation。这一章是对unknown MDP找到一个最优的policy, optimise value function.
1.2 On and Off-Policy Learning
On-policy learning
- learn on the job
- learn about policy π \pi π from experience sampled from π \pi π
Off-policy learning - look over someone’s shoulder
- learn about policy π \pi π from experience sampled from μ \mu μ
2 On-policy Monte-Carlo Control
一般的policy iteraion的框架
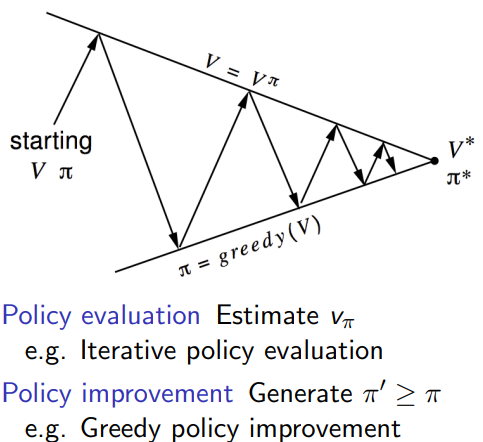
2.1 mc条件下如何进行policy iteration
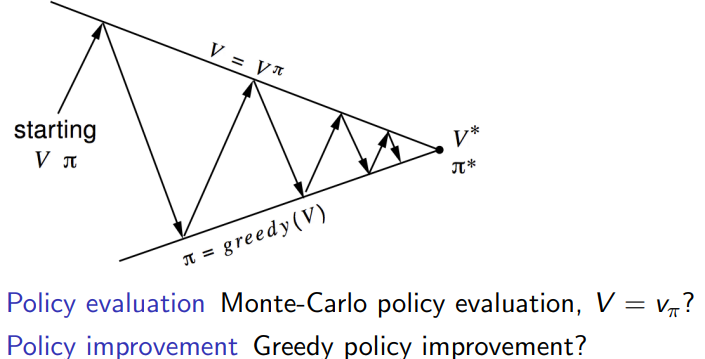
之前在做Policy evaluation的时候,用的是state value function V π V_{\pi} Vπ.
切换到Greedy policy improvement, 还是用这个吗?主要问题是状态转移矩阵和reward都不知道,
选择Q(s,a)最起码不需要显式的知道状态转移矩阵和reward。
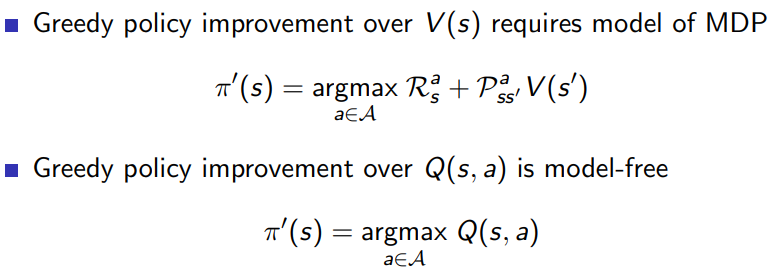
有一些方法可以学习Q(s,a),通过过往经验根据统计的方法去估计,或者神经网络去估计。
蒙特卡洛方法(Monte Carlo Methods):这种方法通过从实际经验中采样完整的episode,并利用该episode的平均回报来估计Q(s, a)。蒙特卡洛方法对每个状态-动作对都进行独立的评估,并且只在episode结束时更新Q值。
Temporal-Difference(TD)学习:TD学习是一种在线学习方法,它在每一步都更新Q值。这种方法在每次状态转换(s, a, r, s’)时更新Q值,使用TD误差(即当前奖励加上下一个状态-动作对的折扣Q值减去当前状态-动作对的Q值)。
Q-learning:Q-learning是一种TD学习方法,但它学习的是一个估计的最优Q值函数,而不是策略的Q值。在每个时间步,Q-learning更新Q值时,会采用greedy策略选择下一个状态的最大Q值,而不是使用当前策略选择的Q值。

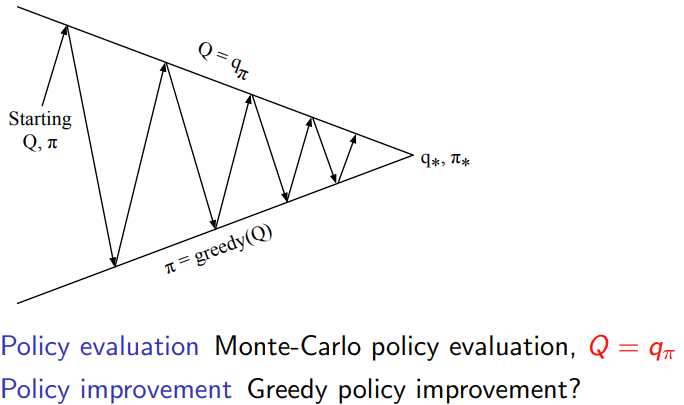
2.2 exploration
只采用greedy action selection在MDP条件下,显然是最佳的;对于POMDP存在一些问题了。
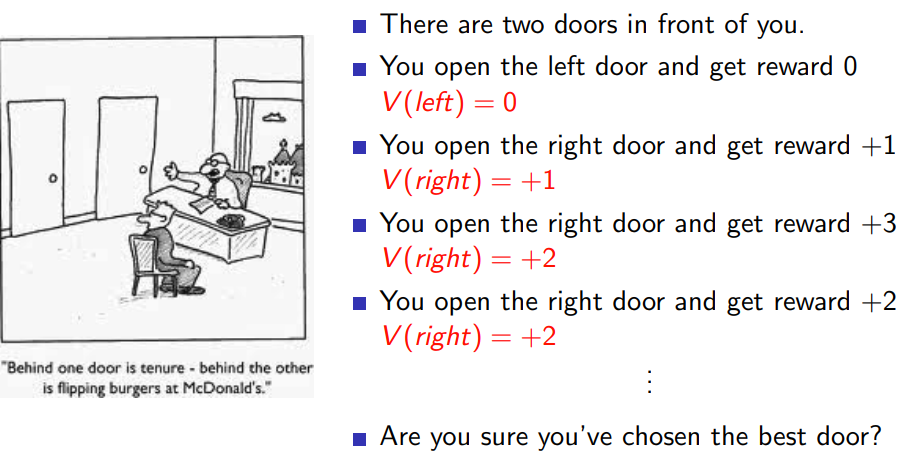
2.2.1 ϵ − \epsilon- ϵ−Greedy exploration

用这种方法来解决driving home policy iteration的问题
import numpy as npn_states = 4
n_actions = 2
n_episodes = 5000
epsilon = 0.1
gamma = 0.9# Step function
def step(state, action):if action == 0: # Acceleratenext_state = max(state - 1, 0)else: # Deceleratenext_state = min(state + 1, n_states - 1)reward = -1 if next_state != 0 else 0return next_state, reward# Epsilon-greedy policy
def epsilon_greedy_policy(Q, state, epsilon):if np.random.rand() < epsilon:return np.random.randint(n_actions)else:return np.argmax(Q[state, :])# Monte Carlo Policy Iteration with epsilon-greedy policy
Q = np.zeros((n_states, n_actions))
returns = np.zeros((n_states, n_actions))
counts = np.zeros((n_states, n_actions))for _ in range(n_episodes):state = n_states - 1episode = []while state != 0:action = epsilon_greedy_policy(Q, state, epsilon)next_state, reward = step(state, action)episode.append((state, action, reward))state = next_stateG = 0for t in reversed(range(len(episode))):state, action, reward = episode[t]G = gamma * G + rewardcounts[state, action] += 1returns[state, action] += GQ[state, action] = returns[state, action] / counts[state, action]policy = np.argmax(Q, axis=1)
print("Optimal policy:", policy)
这里代码采用了一种隐士的方法来实现 ϵ − \epsilon- ϵ−exploration
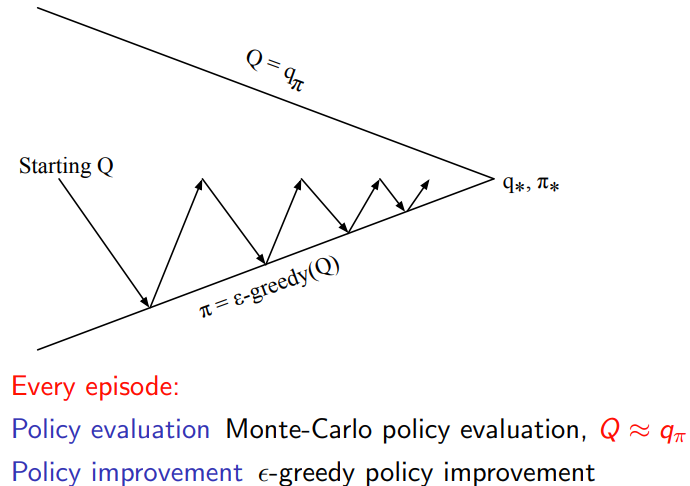
2.2.2 ϵ − \epsilon- ϵ−policy improvement

确定一个完整的MC pipeline
2.2.3 GLIE
Greedy in the Limit with Infinite Exploration (GLIE)
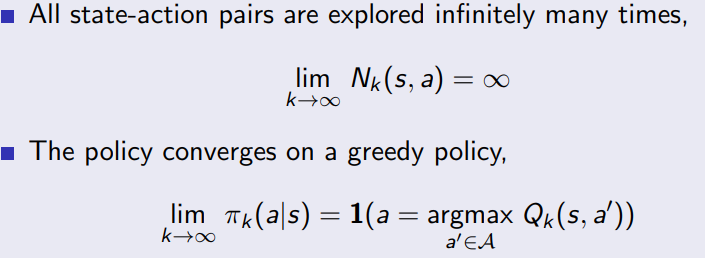
GLIE Monte-Carlo Control(Greedy in the Limit with Infinite Exploration,具有无限探索的极限贪心)和ε-greedy策略都是强化学习中用于平衡探索和利用的策略。这两种方法之间的区别和联系如下:
1.GLIE Monte-Carlo Control是一种强化学习算法,它使用一种特殊的探索策略来确保所有状态-动作对都被无限次探索。具体来说,GLIE算法要求在算法执行过程中逐渐减小探索率ε,使得在无限时间内,探索率趋向于0。这意味着,随着时间的推移,GLIE Monte-Carlo Control将越来越倾向于选择最优动作。
2.ε-greedy策略是一种常用的探索-利用平衡策略。它以ε的概率随机选择一个动作(探索),以1-ε的概率选择具有最高Q值的动作(利用)。ε-greedy策略可以用在各种强化学习算法中,包括GLIE Monte-Carlo Control。
总的来说,GLIE Monte-Carlo Control是一种强化学习算法,而ε-greedy策略是一种在该算法中可以使用的探索-利用平衡策略。在GLIE Monte-Carlo Control中,ε-greedy策略需要满足特定条件(即逐渐降低探索率ε),以确保在算法收敛时找到最优策略。
对于 ϵ \epsilon ϵ逐渐收敛到0的形式,就是GLIE
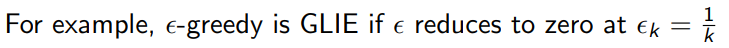

用GLIE重新实现刚才的代码
import numpy as npn_states = 6
n_actions = 2
n_episodes = 5000
gamma = 0.9# step function
def step(state, action):if action == 0: # drivenext_state = min(state + np.random.randint(1, 7), n_states - 1)reward = -1else: # waitnext_state = statereward = -2return next_state, reward# epsilon-greedy action selection
def epsilon_greedy(Q, state, epsilon):if np.random.rand() < epsilon:return np.random.randint(n_actions)else:return np.argmax(Q[state, :])# GLIE Monte-Carlo Control
Q = np.zeros((n_states, n_actions))
returns = {}
counts = np.ones((n_states, n_actions))for episode in range(n_episodes):state = 0trajectory = []while state != n_states - 1:epsilon = 1 / np.min(counts[state, :])action = epsilon_greedy(Q, state, epsilon)next_state, reward = step(state, action)trajectory.append((state, action, reward))state = next_stateG = 0for t in reversed(range(len(trajectory))):state, action, reward = trajectory[t]G = gamma * G + reward# Check if this state-action pair is first visited in this episodeif not any(x[0] == state and x[1] == action for x in trajectory[:t]):if (state, action) not in returns:returns[(state, action)] = []returns[(state, action)].append(G)Q[state, action] = np.mean(returns[(state, action)])counts[state, action] += 1print("Q-values:")
print(Q)policy = np.argmax(Q, axis=1)
print("Policy:", policy)
3 On-policy Temporal-Difference Learning
3.1 MC vs TD control
TD 相对于 MC的优势
- Lower variance
- Online
- Incomplete sequences
Natural idea: use TD instead of MC on our control loop - Apply TD to Q(S, A)
- Use ϵ − \epsilon- ϵ−greedy policy improvement
- Update every time-step
3.2 Sarsa( λ \lambda λ)
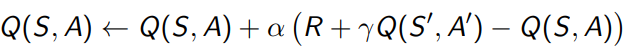
对比一下TD(\lambda)的policy evaluation的公式
E 0 ( s ) = 0 E t ( s ) = γ λ E t − 1 ( s ) + 1 ( s t = s ) δ t = R t + 1 + γ V ( S t + 1 ) − V ( S t ) V ( s ) = V ( s ) + α ∗ δ t ∗ E t ( s ) \begin{aligned} E_0(s)&=0\\ E_t(s)&=\gamma \lambda E_{t-1}(s)+1(s_t=s) \\ \delta_t &= R_{t+1}+\gamma V(S_{t+1})-V(S_t) \\ V(s) &=V(s)+ \alpha * \delta_t * E_t(s) \end{aligned} E0(s)Et(s)δtV(s)=0=γλEt−1(s)+1(st=s)=Rt+1+γV(St+1)−V(St)=V(s)+α∗δt∗Et(s)
现在不用state value function,更换成
V ( S t ) = Q ( S , A ) V ( S ′ ) = Q ( S ′ , A ′ ) \begin{aligned} V(S_t) &=Q(S,A) \\ V(S') & = Q(S', A') \end{aligned} V(St)V(S′)=Q(S,A)=Q(S′,A′)
实现之前的driving home的代码

import numpy as npn_states = 6
n_actions = 2
n_episodes = 5000
gamma = 0.9
alpha = 0.1
_lambda = 0.9# step function
def step(state, action):if action == 0: # drivenext_state = min(state + np.random.randint(1, 7), n_states - 1)reward = -1else: # waitnext_state = statereward = -2return next_state, reward# epsilon-greedy action selection
def epsilon_greedy(Q, state, epsilon):if np.random.rand() < epsilon:return np.random.randint(n_actions)else:return np.argmax(Q[state, :])# Sarsa(lambda) algorithm
Q = np.zeros((n_states, n_actions))
counts = np.ones((n_states, n_actions))for episode in range(n_episodes):state = 0epsilon = 1 / np.min(counts[state, :])action = epsilon_greedy(Q, state, epsilon)E = np.zeros((n_states, n_actions))while state != n_states - 1:next_state, reward = step(state, action)epsilon = 1 / np.min(counts[next_state, :])next_action = epsilon_greedy(Q, next_state, epsilon)delta = reward + gamma * Q[next_state, next_action] - Q[state, action]E[state, action] = E[state, action] * (gamma * _lambda) + 1Q += alpha * delta * Ecounts[state, action] += 1E *= gamma * _lambdastate, action = next_state, next_actionprint("Q-values:")
print(Q)policy = np.argmax(Q, axis=1)
print("Policy:", policy)
3.2.1 converges

forward view sarsa,平衡当前的reward和未来的影响Q

backward view, 和 T D ( λ ) TD(\lambda) TD(λ)类似

4 Off-Policy Learning
4.1 离线学习的作用和意义

Off-policy学习是强化学习中的一种方法,指的是在学习过程中,学习者并不完全遵循当前的策略进行决策。换句话说,它可以从其他策略生成的数据中学习,而不仅仅是从当前策略中学习。这种学习方法的优点是能够在训练过程中有效地利用历史数据,并且有助于学习更强大、更稳定的策略。
import numpy as np
import gym# 创建FrozenLake-v1环境
env = gym.make("FrozenLake-v1")# 初始化 Q-table
num_states = env.observation_space.n
num_actions = env.action_space.n
q_table = np.zeros((num_states, num_actions))# 超参数设置
num_episodes = 5000
alpha = 0.1 # 学习率
gamma = 0.99 # 折扣因子
epsilon = 1 # 探索率
min_epsilon = 0.01 # 最小探索率
decay_rate = 0.999 # 探索率衰减率# Q-learning算法
for episode in range(num_episodes):state = env.reset()done = Falseif isinstance(state, tuple):state = state[0]while not done:# 采用epsilon-greedy策略选择动作if np.random.uniform(0, 1) < epsilon:action = env.action_space.sample() # 随机选择一个动作else:action = np.argmax(q_table[state]) # 选择Q值最大的动作# 执行动作,观察新状态和奖励next_state, reward, done, _, _ = env.step(action)# 更新 Q-tableq_table[state, action] += alpha * (reward + gamma * np.max(q_table[next_state]) - q_table[state, action])# 更新状态state = next_state# 更新探索率epsilon = max(min_epsilon, epsilon * decay_rate)# 输出训练后的 Q-table
print("训练后的Q-table:")
print(q_table)# 测试训练好的智能体
num_test_episodes = 3
for episode in range(num_test_episodes):state = env.reset()if isinstance(state, tuple):state = state[0]done = Falseprint(f"\n测试智能体, 试验 {episode + 1}:")while not done:action = np.argmax(q_table[state]) # 选择Q值最大的动作next_state, _, done, _, _ = env.step(action)env.render() # 渲染环境state = next_stateenv.close()
对比sarsa(0)的Python代码
import numpy as np
import gym# 创建FrozenLake-v1环境
env = gym.make("FrozenLake-v1")# 初始化 Q-table
num_states = env.observation_space.n
num_actions = env.action_space.n
q_table = np.zeros((num_states, num_actions))# 超参数设置
num_episodes = 5000
alpha = 0.1 # 学习率
gamma = 0.99 # 折扣因子
epsilon = 1 # 探索率
min_epsilon = 0.01 # 最小探索率
decay_rate = 0.999 # 探索率衰减率# SARSA(0)算法
for episode in range(num_episodes):state = env.reset()done = False# 使用epsilon-greedy策略选择初始动作if np.random.uniform(0, 1) < epsilon:action = env.action_space.sample() # 随机选择一个动作else:action = np.argmax(q_table[state]) # 选择Q值最大的动作while not done:# 执行动作,观察新状态和奖励next_state, reward, done, _ = env.step(action)# 使用epsilon-greedy策略选择下一个动作if np.random.uniform(0, 1) < epsilon:next_action = env.action_space.sample() # 随机选择一个动作else:next_action = np.argmax(q_table[next_state]) # 选择Q值最大的动作# 更新 Q-tableq_table[state, action] += alpha * (reward + gamma * q_table[next_state, next_action] - q_table[state, action])# 更新状态和动作state = next_stateaction = next_action# 更新探索率epsilon = max(min_epsilon, epsilon * decay_rate)# 输出训练后的 Q-table
print("训练后的Q-table:")
print(q_table)# 测试训练好的智能体
num_test_episodes = 3
for episode in range(num_test_episodes):state = env.reset()done = Falseprint(f"\n测试智能体, 试验 {episode + 1}:")while not done:action = np.argmax(q_table[state]) # 选择Q值最大的动作next_state, _, done, _ = env.step(action)env.render() # 渲染环境state = next_stateenv.close()
代码对比可以看出
# sarsa(0)# 更新 Q-tableq_table[state, action] += alpha * (reward + gamma * q_table[next_state, next_action] - q_table[state, action])# 更新状态和动作state = next_stateaction = next_action# 更新探索率epsilon = max(min_epsilon, epsilon * decay_rate)# Q-learning# 更新 Q-tableq_table[state, action] += alpha * (reward + gamma * np.max(q_table[next_state]) - q_table[state, action])# 更新状态state = next_state# 更新探索率epsilon = max(min_epsilon, epsilon * decay_rate)
Q-learning的off-policy特性体现在它能从其他策略生成的经验中学习。在Q-learning中,更新Q值时我们考虑了最大化下一状态的Q值,而不是基于当前策略实际采取的动作。这意味着Q-learning在更新过程中既考虑了当前策略下的动作,也考虑了其他策略下的动作。这使得Q-learning能够学习到最优策略,而不仅仅局限于当前策略。
在更新Q-table时,我们使用了np.max(q_table[next_state])来计算下一状态的最大Q值。这个最大Q值可能来自于其他策略,而不仅仅是当前的策略。这就是Q-learning如何体现off-policy特性的。
# 执行动作,观察新状态和奖励
next_state, reward, done, _ = env.step(action)# 更新 Q-table
q_table[state, action] += alpha * (reward + gamma * np.max(q_table[next_state]) - q_table[state, action])4.2 importance sampling
4.2.1 definition
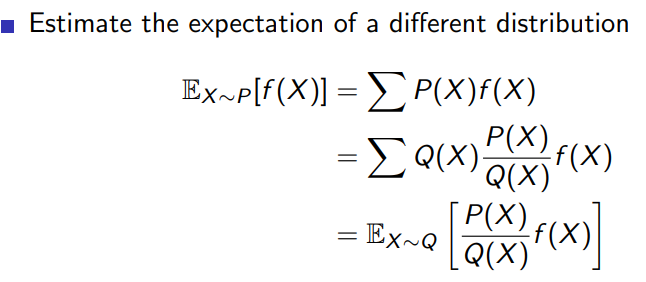
4.2.2 importance sampling for off-policy Monte-Carlo
在强化学习中,重要性采样(Importance Sampling)是一种数学技术,用于从一个分布中估计另一个分布的期望值。在强化学习的背景下,重要性采样通常用于从一个策略(行为策略,称为b)中生成的经验样本来估计另一个策略(目标策略,称为π)的期望回报。这在off-policy学习算法中尤为重要,因为我们需要从一个策略的经验中学习另一个策略。
重要性采样的基本思想是通过对目标策略和行为策略的概率比值(称为重要性采样比率)进行加权,来修正从行为策略生成的样本。这样一来,我们就可以使用这些加权样本来估计目标策略的期望回报。
设想我们有一个序列(轨迹):s_0, a_0, r_1, s_1, a_1, r_2, …, s_{T-1}, a_{T-1}, r_T, s_T,其中s_i表示状态,a_i表示动作,r_{i+1}表示奖励。我们可以计算这个序列在目标策略和行为策略下的概率,分别表示为P_π和P_b。重要性采样比率(IS)定义为目标策略和行为策略概率的比值:
IS = P π P b \text{IS} = \frac{P_\pi}{P_b} IS=PbPπ
在强化学习中,我们通常使用累积折扣回报(G_t)来评估策略。为了估计目标策略的累积折扣回报,我们可以使用行为策略生成的轨迹和重要性采样比率来加权:
E [ G t π ] ≈ 1 N ∑ i = 1 N ( G t b ⋅ IS ) \mathbb{E}[G_t^\pi] \approx \frac{1}{N} \sum_{i=1}^{N} \left( G_t^b \cdot \text{IS} \right) E[Gtπ]≈N1i=1∑N(Gtb⋅IS)
其中N表示轨迹数量,G_t^{π} 表示目标策略的累积折扣回报,G_t^b表示行为策略的累积折扣回报。
累积折扣回报 G t b G_t^b Gtb,可以通过累计回报的定义,或者MC算法进行计算
G t b = r t + 1 + γ r t + 2 + γ 2 r t + 3 + ⋯ + γ T − t − 1 r T G_t^b = r_{t+1} + \gamma r_{t+2} + \gamma^2 r_{t+3} + \cdots + \gamma^{T-t-1} r_T Gtb=rt+1+γrt+2+γ2rt+3+⋯+γT−t−1rT
G_tπ表示在时间步t开始,根据目标策略π在未来所有时间步中获得的累积折扣回报。直接计算G_tπ可能很困难,因为我们可能没有关于目标策略π的经验数据。然而,我们可以使用重要性采样(Importance Sampling)来间接估计G_t^π。通过利用行为策略b生成的轨迹和重要性采样比率(IS),我们可以计算加权的累积折扣回报,从而估计目标策略π的期望回报。
在计算G_tπ时,我们需要先计算G_tb,然后使用重要性采样比率(IS)对其进行加权。重要性采样比率是目标策略π和行为策略b在每个时间步上的概率比值的乘积。我们可以通过以下方式计算G_t^π的估计值:
E [ G t π ] ≈ 1 N ∑ i = 1 N ( G t b ⋅ IS ) \mathbb{E}[G_t^\pi] \approx \frac{1}{N} \sum_{i=1}^{N} \left( G_t^b \cdot \text{IS} \right) E[Gtπ]≈N1i=1∑N(Gtb⋅IS)
其中,N表示轨迹数量,G_t^b表示行为策略b的累积折扣回报,IS表示重要性采样比率。
为了计算重要性采样比率,我们需要分别计算目标策略π和行为策略b在每个时间步上采取相应动作的概率。设π(a_t|s_t)表示在状态s_t下,根据目标策略π采取动作a_t的概率,而b(a_t|s_t)表示在状态s_t下,根据行为策略b采取动作a_t的概率。那么,重要性采样比率可以通过以下公式计算:
IS = ∏ k = t T − 1 π ( a k ∣ s k ) b ( a k ∣ s k ) \text{IS} = \prod_{k=t}^{T-1} \frac{\pi(a_k|s_k)}{b(a_k|s_k)} IS=k=t∏T−1b(ak∣sk)π(ak∣sk)

使用一个例子,假设我们有一个简单的马尔可夫决策过程(MDP),共有两个状态A和B。在每个状态下,智能体可以采取两个动作:向左(L)或向右(R)。智能体按照行为策略b来选择动作,而我们希望估计目标策略π的期望回报。
π(A, L) = 0.9, π(A, R) = 0.1
π(B, L) = 0.5, π(B, R) = 0.5b(A, L) = 0.5, b(A, R) = 0.5
b(B, L) = 0.7, b(B, R) = 0.3
# 定义目标策略π和行为策略b
pi = {('A', 'L'): 0.9,('A', 'R'): 0.1,('B', 'L'): 0.5,('B', 'R'): 0.5,
}b = {('A', 'L'): 0.5,('A', 'R'): 0.5,('B', 'L'): 0.7,('B', 'R'): 0.3,
}# 按照行为策略b生成的轨迹
trajectory = [('A', 'L'), ('B', 'R'), ('A', 'L')]# 计算重要性采样比率
def importance_sampling_ratio(trajectory, pi, b):is_ratio = 1.0for state, action in trajectory:is_ratio *= pi[state, action] / b[state, action]return is_ratio# 计算轨迹的重要性采样比率
is_ratio = importance_sampling_ratio(trajectory, pi, b)
print("Importance Sampling Ratio:", is_ratio)
实际工程中,概率如何获得
在实际应用中,使用重要性采样时确实需要知道行为策略(b)和目标策略(π)在每个状态下选择动作的概率。通常,这些概率可以从策略本身获得。对于离策略学习,我们在采样过程中使用行为策略,因此可以在生成轨迹时记录这些概率。
对于目标策略(π),我们通常根据当前的价值函数或Q函数来确定。例如,在Q-Learning中,我们希望学习最优策略,因此目标策略是在每个状态下选择具有最高Q值的动作。这种情况下,目标策略是确定性的,所以在给定状态下选择最优动作的概率为1,其他动作的概率为0。
行为策略(b)通常更容易获取,因为我们在生成轨迹时使用它来选择动作。例如,在使用Epsilon-greedy策略时,我们知道在给定状态下选择最优动作的概率为1 - epsilon + epsilon / n_actions,而选择其他动作的概率为epsilon / n_actions。我们可以在采样过程中记录这些概率。
def generate_trajectory_with_behavior_policy(env, q_table, epsilon):trajectory = []state = env.reset()done = Falsewhile not done:action = epsilon_greedy_policy(state, q_table, epsilon)# 计算行为策略概率optimal_action = np.argmax(q_table[state])if action == optimal_action:behavior_prob = 1 - epsilon + epsilon / n_actionselse:behavior_prob = epsilon / n_actionsnext_state, reward, done, _ = env.step(action)trajectory.append((state, action, reward, behavior_prob))state = next_statereturn trajectory
再来看一个importance sampling 和expect sarsa结合起来的例子
import numpy as np
import gym# 初始化环境
env = gym.make('FrozenLake-v1')# 初始化参数
n_states = env.observation_space.n
n_actions = env.action_space.n
alpha = 0.1 # 学习率
gamma = 0.99 # 折扣因子
epsilon = 0.1 # Epsilon-greedy策略参数
episodes = 20000 # 迭代次数# 初始化Q表
q_table = np.zeros((n_states, n_actions))# Epsilon-greedy策略
def epsilon_greedy_policy(state, q_table, epsilon):if np.random.rand() < epsilon:return np.random.randint(n_actions)else:return np.argmax(q_table[state])# 通过重要性采样更新Q值
def update_q_table_with_importance_sampling(state, action, reward, next_state, q_table, alpha, gamma, epsilon):# 使用Q-Learning选择下一个动作next_action = np.argmax(q_table[next_state])# 使用Epsilon-greedy策略选择下一个动作behavior_next_action = epsilon_greedy_policy(next_state, q_table, epsilon)# 计算目标策略和行为策略的概率target_policy_prob = 1.0 if action == next_action else 0.0behavior_policy_prob = 1 - epsilon + epsilon / n_actions if action == behavior_next_action else epsilon / n_actions# 计算重要性采样比率importance_sampling_ratio = target_policy_prob / behavior_policy_prob# 计算TD目标和TD误差td_target = reward + gamma * q_table[next_state, next_action]td_error = td_target - q_table[state, action]# 使用重要性采样更新Q值q_table[state, action] += alpha * importance_sampling_ratio * td_error# 开始学习
for episode in range(episodes):state = env.reset()done = Falsewhile not done:# 选择动作action = epsilon_greedy_policy(state, q_table, epsilon)# 执行动作并观察结果next_state, reward, done, _ = env.step(action)# 更新Q表update_q_table_with_importance_sampling(state, action, reward, next_state, q_table, alpha, gamma, epsilon)# 更新状态state = next_stateprint("Q-Table:")
print(q_table)
在来看一下q-table的公式
q table ( s t , a t ) ← q table ( s t , a t ) + α ⋅ ρ ⋅ TD error q_{\text{table}}(s_t, a_t) \leftarrow q_{\text{table}}(s_t, a_t) + \alpha \cdot \rho \cdot \text{TD}_\text{error} qtable(st,at)←qtable(st,at)+α⋅ρ⋅TDerror
TDtarget = r t + 1 + γ ⋅ E a t + 1 ∼ π [ q table ( s t + 1 , a t + 1 ) ] \text{TD}\text{target} = r_{t+1} + \gamma \cdot \mathbb{E}_{a_{t+1} \sim \pi}[q_{\text{table}}(s_{t+1}, a_{t+1})] TDtarget=rt+1+γ⋅Eat+1∼π[qtable(st+1,at+1)]
在这个公式中,TD目标表示我们希望学习到的理想Q值,它是由当前奖励加上折扣期望回报组成的。在更新Q值时,我们会根据TD目标和当前Q值之间的差异(即TD误差)来调整Q值。
5 Summary
相关文章:

David Silver Lecture 5: Model-Free Control
1 Introduction 1.1 内容 上一章是对一个unknown MDP进行value function的预测,相当于policy evaluation。这一章是对unknown MDP找到一个最优的policy, optimise value function. 1.2 On and Off-Policy Learning On-policy learning learn on the…...

MySQL-----事务管理
文章目录 前言一、什么是事务二、为什么会出现事务三、事物的版本支持四、事物的提交方式五、事务常见的操作方式六、事务隔离级别如何理解隔离性1隔离级别查看与设置隔离性读未提交【Read Uncommitted】读提交【Read Committed】可重复读【Repeatable Read】串行化【serializa…...
chatGPT润色中英论文软件-文章修改润色器
chatGPT可以润色英文论文吗? ChatGPT可以润色英文论文,它具备自动纠错、自动完善语法和严格全面的语法、句法和内容结构检查等功能,可以对英文论文进行高质量的润色和优化。此外,ChatGPT还支持学术翻译润色、查重及语言改写等服务…...

MacOS下安装和配置Nginx
一、安装brew /bin/zsh -c "$(curl -fsSL https://gitee.com/cunkai/HomebrewCN/raw/master/Homebrew.sh)"按回车后,根据提示操作:输入镜像序号 --> 输入Y,回车等待brew安装完成即可。 在终端输入brew -v后,会提示…...
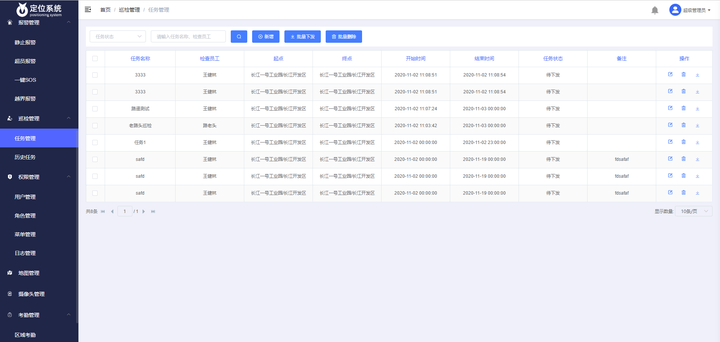
采用UWB(超宽频)技术开发的java版智慧工厂定位系统源码
室内定位系统源码,采用UWB定位技术开发的智慧工厂定位系统源码 技术架构:单体服务 硬件(UWB定位基站、卡牌) 开发语言:java 开发工具:idea 、VS Code 前端框架:vue 后端框架:s…...

【2023华为OD笔试必会20题--C语言版】《04 日志采集系统》——数组
本专栏收录了华为OD 2022 Q4和2023Q1笔试题目,100分类别中的出现频率最高(至少出现100次)的20道,每篇文章包括原始题目 和 我亲自编写并在Visual Studio中运行成功的C语言代码。 仅供参考、启发使用,切不可照搬、照抄,查重倒是可以过,但后面的技术面试还是会暴露的。✨✨…...
)
MySQL数据库——MySQL修改存储过程(ALTER PROCEDURE)
在实际开发过程中,业务需求修改的情况时有发生,所以修改 MySQL 中的存储过程是不可避免的。 MySQL 中通过 ALTER PROCEDURE 语句来修改存储过程。下面将详细讲解修改存储过程的方法。 MySQL 中修改存储过程的语法格式如下: ALTER PROCEDURE…...
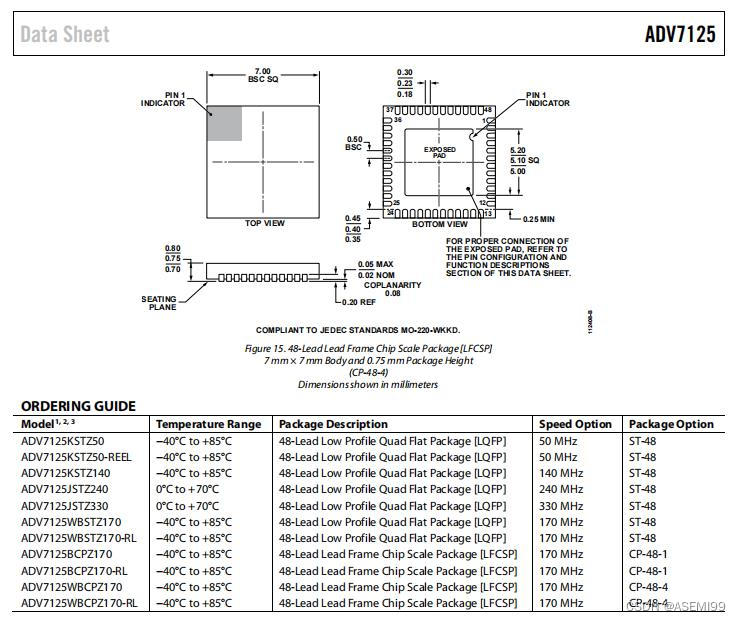
ASEMI代理ADV7125JSTZ330原装ADI车规级ADV7125JSTZ330
编辑:ll ASEMI代理ADV7125JSTZ330原装ADI车规级ADV7125JSTZ330 型号:ADV7125JSTZ330 品牌:ADI/亚德诺 封装:LQFP-48 批号:2023 引脚数量:48 工作温度:-40C~85C 安装类型:表面…...

86盒IP对讲一键报警器
86盒IP对讲一键报警器 86盒IP对讲一键报警器:革命性保障生命安全的利器! 随着科技的飞速发展,我们的生活变得越来越方便和智能化。而86盒IP对讲一键报警器更是在这种背景下应运而生。这款产品不仅无缝对接各种手机APP,也可以在智…...

【高数+复变函数】傅里叶积分
文章目录 【高数复变函数】傅里叶积分2. 傅里叶积分2.1 复数形式积分公式2.2 三角形式 上一节: 【高数复变函数】傅里叶级数 【高数复变函数】傅里叶积分 2. 傅里叶积分 在上一节中,我们知道了傅里叶级数的基本知识,其中,周期为…...

【Leetcode】241. 为运算表达式设计优先级
241. 为运算表达式设计优先级(中等) 解法一:分治法 对于这道题,加括号其实就是决定运算次序,所以我们可以把加括号转化为,「对于每个运算符号,先执行处理两侧的数学表达式,再处理此…...

torch两个向量除法,对于分母向量中的元素为0是设置为1,避免运算错误
在gpu运行时,如果在进行两个向量除法的时候,对于分母向量中的元素为0是设置为1,避免运算错误。 可以使用torch的division函数以及clamp函数来解决这个问题。具体步骤如下: 使用division函数将分子向量除以分母向量。 使用clamp函…...

NodeJs 最近各版本特性汇总
(预测未来最好的方法就是把它创造出来——尼葛洛庞帝) NodeJs 官方链接 github链接 V8链接 Node.js发布于2009年5月,由Ryan Dahl开发,是一个基于Chrome V8引擎的JavaScript运行环境,使用了一个事件驱动、非阻塞式I/O模…...

python数据分析案例——天猫订单综合分析
前言 大家早好、午好、晚好吖 ❤ ~欢迎光临本文章 什么是数据分析 明确目的–获得数据(爬虫,现有,公开的数据)–数据预处理——数据可视化——结论 准备 环境使用: 在开始写我们的代码之前,我们要准备好运行代码的程序 Anacon…...
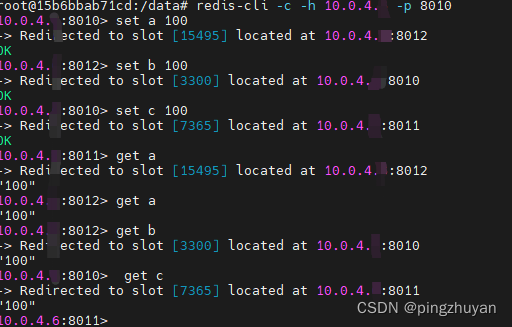
05- redis集群模式搭建(上) (包含云服务器[填坑])
目录 1. 准备环境: 2. 简介: -> 2.1 前言: -> 2.2 Redis集群架构实现了对redis的水平扩容 -> 2.3 redis cluster集群原理 3. 搭建后特别需要注意的问题 ->3.1 [重点]: 如果一个服务出现故障: 是否可以继续提供服务??? ---> 3.1.1 如果集群中故障re…...

【AI】YOLOV1原理详解
AI学习目录汇总 0、前言 YOLOv1~3作者是约瑟夫雷德蒙(Joseph Chet Redmon),他的网站:https://pjreddie.com/ YOLOv1网站:https://pjreddie.com/darknet/yolov1/ YOLOv2网站:https://pjreddie.com/darknet…...
提高APP安全性的必备加固手段——深度解析代码混淆技术
APP 加固方式 Android APP 加固是优化 APK 安全性的一种方法,常见的加固方式有混淆代码、加壳、数据加密、动态加载等。下面介绍一下 Android APP 加固的具体实现方式。 混淆代码: 使用 ProGuard 工具可以对代码进行混淆,使得反编译出来的代…...

想让行车记录仪协助道路病害自动化检测?可以!
针对【RGB3DS道路表观病害信息智慧检测系统】,我们着重介绍过其与道路检测车做集成预装或者处理道路检测车数据的极大便利,其中之一便是可高效输出带有道路检测车桩号标记的病害报表,这是因为道路检测车数据本身具有规范性。 那么如果使用道…...
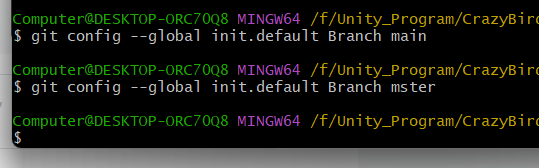
git上传大大大文件项目好折磨人
本来想把unity项目的源码上传上gitee啊,但是那个项目有1个多G,还是个半成品,要是写完,都不知道行不行 正常的上传 所用到的命令: 1、 git init 初始化,创建本地仓库 2、 git add . 添加到本地仓库 3、 git…...

java常见异常的处理方法
以下是一些常见的异常处理方法: 捕获和处理异常(try-catch): 使用try-catch语句块可以捕获并处理异常。在try块中编写可能抛出异常的代码,然后在catch块中指定异常类型,以便捕获并处理异常。 try {// 可能抛…...

微信小程序之bind和catch
这两个呢,都是绑定事件用的,具体使用有些小区别。 官方文档: 事件冒泡处理不同 bind:绑定的事件会向上冒泡,即触发当前组件的事件后,还会继续触发父组件的相同事件。例如,有一个子视图绑定了b…...
)
云计算——弹性云计算器(ECS)
弹性云服务器:ECS 概述 云计算重构了ICT系统,云计算平台厂商推出使得厂家能够主要关注应用管理而非平台管理的云平台,包含如下主要概念。 ECS(Elastic Cloud Server):即弹性云服务器,是云计算…...

Qwen3-Embedding-0.6B深度解析:多语言语义检索的轻量级利器
第一章 引言:语义表示的新时代挑战与Qwen3的破局之路 1.1 文本嵌入的核心价值与技术演进 在人工智能领域,文本嵌入技术如同连接自然语言与机器理解的“神经突触”——它将人类语言转化为计算机可计算的语义向量,支撑着搜索引擎、推荐系统、…...
基础光照(Basic Lighting))
C++.OpenGL (10/64)基础光照(Basic Lighting)
基础光照(Basic Lighting) 冯氏光照模型(Phong Lighting Model) #mermaid-svg-GLdskXwWINxNGHso {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-GLdskXwWINxNGHso .error-icon{fill:#552222;}#mermaid-svg-GLd…...

Pinocchio 库详解及其在足式机器人上的应用
Pinocchio 库详解及其在足式机器人上的应用 Pinocchio (Pinocchio is not only a nose) 是一个开源的 C 库,专门用于快速计算机器人模型的正向运动学、逆向运动学、雅可比矩阵、动力学和动力学导数。它主要关注效率和准确性,并提供了一个通用的框架&…...

Mysql中select查询语句的执行过程
目录 1、介绍 1.1、组件介绍 1.2、Sql执行顺序 2、执行流程 2.1. 连接与认证 2.2. 查询缓存 2.3. 语法解析(Parser) 2.4、执行sql 1. 预处理(Preprocessor) 2. 查询优化器(Optimizer) 3. 执行器…...

算法:模拟
1.替换所有的问号 1576. 替换所有的问号 - 力扣(LeetCode) 遍历字符串:通过外层循环逐一检查每个字符。遇到 ? 时处理: 内层循环遍历小写字母(a 到 z)。对每个字母检查是否满足: 与…...

uni-app学习笔记三十五--扩展组件的安装和使用
由于内置组件不能满足日常开发需要,uniapp官方也提供了众多的扩展组件供我们使用。由于不是内置组件,需要安装才能使用。 一、安装扩展插件 安装方法: 1.访问uniapp官方文档组件部分:组件使用的入门教程 | uni-app官网 点击左侧…...

深入理解 React 样式方案
React 的样式方案较多,在应用开发初期,开发者需要根据项目业务具体情况选择对应样式方案。React 样式方案主要有: 1. 内联样式 2. module css 3. css in js 4. tailwind css 这些方案中,均有各自的优势和缺点。 1. 方案优劣势 1. 内联样式: 简单直观,适合动态样式和…...

RushDB开源程序 是现代应用程序和 AI 的即时数据库。建立在 Neo4j 之上
一、软件介绍 文末提供程序和源码下载 RushDB 改变了您处理图形数据的方式 — 不需要 Schema,不需要复杂的查询,只需推送数据即可。 二、Key Features ✨ 主要特点 Instant Setup: Be productive in seconds, not days 即时设置 :在几秒钟…...
