正则化解决过拟合
本片举三个例子进行对比,分别是:不使用正则化、使用L2正则化、使用dropout正则化。
首先是前后向传播、加载数据、画图所需要的相关函数的reg_utils.py:
# -*- coding: utf-8 -*-import numpy as np
import matplotlib.pyplot as plt
import scipy.io as siodef sigmoid(x):"""Compute the sigmoid of xArguments:x -- A scalar or numpy array of any size.Return:s -- sigmoid(x)"""s = 1/(1+np.exp(-x))return sdef relu(x):"""Compute the relu of xArguments:x -- A scalar or numpy array of any size.Return:s -- relu(x)"""s = np.maximum(0,x)return sdef initialize_parameters(layer_dims):"""Arguments:layer_dims -- python array (list) containing the dimensions of each layer in our networkReturns:parameters -- python dictionary containing your parameters "W1", "b1", ..., "WL", "bL":W1 -- weight matrix of shape (layer_dims[l], layer_dims[l-1])b1 -- bias vector of shape (layer_dims[l], 1)Wl -- weight matrix of shape (layer_dims[l-1], layer_dims[l])bl -- bias vector of shape (1, layer_dims[l])Tips:- For example: the layer_dims for the "Planar Data classification model" would have been [2,2,1]. This means W1's shape was (2,2), b1 was (1,2), W2 was (2,1) and b2 was (1,1). Now you have to generalize it!- In the for loop, use parameters['W' + str(l)] to access Wl, where l is the iterative integer."""np.random.seed(3)parameters = {}L = len(layer_dims) # number of layers in the networkfor l in range(1, L):parameters['W' + str(l)] = np.random.randn(layer_dims[l], layer_dims[l-1]) / np.sqrt(layer_dims[l-1])parameters['b' + str(l)] = np.zeros((layer_dims[l], 1))assert(parameters['W' + str(l)].shape == layer_dims[l], layer_dims[l-1])assert(parameters['W' + str(l)].shape == layer_dims[l], 1)return parametersdef forward_propagation(X, parameters):"""Implements the forward propagation (and computes the loss) presented in Figure 2.Arguments:X -- input dataset, of shape (input size, number of examples)Y -- true "label" vector (containing 0 if cat, 1 if non-cat)parameters -- python dictionary containing your parameters "W1", "b1", "W2", "b2", "W3", "b3":W1 -- weight matrix of shape ()b1 -- bias vector of shape ()W2 -- weight matrix of shape ()b2 -- bias vector of shape ()W3 -- weight matrix of shape ()b3 -- bias vector of shape ()Returns:loss -- the loss function (vanilla logistic loss)"""# retrieve parametersW1 = parameters["W1"]b1 = parameters["b1"]W2 = parameters["W2"]b2 = parameters["b2"]W3 = parameters["W3"]b3 = parameters["b3"]# LINEAR -> RELU -> LINEAR -> RELU -> LINEAR -> SIGMOIDz1 = np.dot(W1, X) + b1a1 = relu(z1)z2 = np.dot(W2, a1) + b2a2 = relu(z2)z3 = np.dot(W3, a2) + b3a3 = sigmoid(z3)cache = (z1, a1, W1, b1, z2, a2, W2, b2, z3, a3, W3, b3)return a3, cachedef compute_cost(a3, Y):"""Implement the cost functionArguments:a3 -- post-activation, output of forward propagationY -- "true" labels vector, same shape as a3Returns:cost - value of the cost function"""m = Y.shape[1]logprobs = np.multiply(-np.log(a3),Y) + np.multiply(-np.log(1 - a3), 1 - Y)cost = 1./m * np.nansum(logprobs)return costdef backward_propagation(X, Y, cache):"""Implement the backward propagation presented in figure 2.Arguments:X -- input dataset, of shape (input size, number of examples)Y -- true "label" vector (containing 0 if cat, 1 if non-cat)cache -- cache output from forward_propagation()Returns:gradients -- A dictionary with the gradients with respect to each parameter, activation and pre-activation variables"""m = X.shape[1](z1, a1, W1, b1, z2, a2, W2, b2, z3, a3, W3, b3) = cachedz3 = 1./m * (a3 - Y)dW3 = np.dot(dz3, a2.T)db3 = np.sum(dz3, axis=1, keepdims = True)da2 = np.dot(W3.T, dz3)dz2 = np.multiply(da2, np.int64(a2 > 0))dW2 = np.dot(dz2, a1.T)db2 = np.sum(dz2, axis=1, keepdims = True)da1 = np.dot(W2.T, dz2)dz1 = np.multiply(da1, np.int64(a1 > 0))dW1 = np.dot(dz1, X.T)db1 = np.sum(dz1, axis=1, keepdims = True)gradients = {"dz3": dz3, "dW3": dW3, "db3": db3,"da2": da2, "dz2": dz2, "dW2": dW2, "db2": db2,"da1": da1, "dz1": dz1, "dW1": dW1, "db1": db1}return gradientsdef update_parameters(parameters, grads, learning_rate):"""Update parameters using gradient descentArguments:parameters -- python dictionary containing your parameters grads -- python dictionary containing your gradients, output of n_model_backwardReturns:parameters -- python dictionary containing your updated parameters parameters['W' + str(i)] = ... parameters['b' + str(i)] = ..."""L = len(parameters) // 2 # number of layers in the neural networks# Update rule for each parameterfor k in range(L):parameters["W" + str(k+1)] = parameters["W" + str(k+1)] - learning_rate * grads["dW" + str(k+1)]parameters["b" + str(k+1)] = parameters["b" + str(k+1)] - learning_rate * grads["db" + str(k+1)]return parametersdef load_2D_dataset(is_plot=True):data = sio.loadmat('datasets/data.mat')train_X = data['X'].Ttrain_Y = data['y'].Ttest_X = data['Xval'].Ttest_Y = data['yval'].Tif is_plot:plt.scatter(train_X[0, :], train_X[1, :], c=train_Y, s=40, cmap=plt.cm.Spectral)plt.show()return train_X, train_Y, test_X, test_Ydef predict(X, y, parameters):"""This function is used to predict the results of a n-layer neural network.Arguments:X -- data set of examples you would like to labelparameters -- parameters of the trained modelReturns:p -- predictions for the given dataset X"""m = X.shape[1]p = np.zeros((1,m), dtype = np.int)# Forward propagationa3, caches = forward_propagation(X, parameters)# convert probas to 0/1 predictionsfor i in range(0, a3.shape[1]):if a3[0,i] > 0.5:p[0,i] = 1else:p[0,i] = 0# print resultsprint("Accuracy: " + str(np.mean((p[0,:] == y[0,:]))))return pdef plot_decision_boundary(model, X, y):# Set min and max values and give it some paddingx_min, x_max = X[0, :].min() - 1, X[0, :].max() + 1y_min, y_max = X[1, :].min() - 1, X[1, :].max() + 1h = 0.01# Generate a grid of points with distance h between themxx, yy = np.meshgrid(np.arange(x_min, x_max, h), np.arange(y_min, y_max, h))# Predict the function value for the whole gridZ = model(np.c_[xx.ravel(), yy.ravel()])Z = Z.reshape(xx.shape)# Plot the contour and training examplesplt.contourf(xx, yy, Z, cmap=plt.cm.Spectral)plt.ylabel('x2')plt.xlabel('x1')plt.scatter(X[0, :], X[1, :], c=y, cmap=plt.cm.Spectral)plt.show()def predict_dec(parameters, X):"""Used for plotting decision boundary.Arguments:parameters -- python dictionary containing your parameters X -- input data of size (m, K)Returnspredictions -- vector of predictions of our model (red: 0 / blue: 1)"""# Predict using forward propagation and a classification threshold of 0.5a3, cache = forward_propagation(X, parameters)predictions = (a3>0.5)return predictions
可以先画出数据看是什么样:
train_X, train_Y, test_X, test_Y = reg_utils.load_2D_dataset(is_plot=True)

然后开始测试代码:
不使用正则化
首先我们不使用正则化,让lambd参数(删了个a不与python关键字重合)和keep_prob为默认值0和1,表示不使用这两个正则化。
import numpy as np
import matplotlib.pyplot as plt
import sklearn
import sklearn.datasets
import reg_utils plt.rcParams['figure.figsize'] = (7.0, 4.0) # set default size of plots
plt.rcParams['image.interpolation'] = 'nearest'
plt.rcParams['image.cmap'] = 'gray'# 加载数据集
train_X, train_Y, test_X, test_Y = reg_utils.load_2D_dataset(is_plot=False)def model(X, Y, learning_rate=0.3, num_iterations=30000, print_cost=True, is_plot=True, lambd=0, keep_prob=1):"""实现一个三层的神经网络:LINEAR ->RELU -> LINEAR -> RELU -> LINEAR -> SIGMOID参数:X - 输入的数据,维度为(2, 要训练/测试的数量)Y - 标签,【0(蓝色) | 1(红色)】,维度为(1,对应的是输入的数据的标签)learning_rate - 学习速率num_iterations - 迭代的次数print_cost - 是否打印成本值,每迭代10000次打印一次,但是每1000次记录一个成本值is_polt - 是否绘制梯度下降的曲线图lambd - 正则化的超参数,实数keep_prob - 随机删除节点的概率返回parameters - 学习后的参数"""grads = {}costs = []m = X.shape[1]layers_dims = [X.shape[0], 20, 3, 1]# 初始化参数parameters = reg_utils.initialize_parameters(layers_dims)# 开始学习for i in range(0, num_iterations):# 前向传播## 是否随机删除节点if keep_prob == 1:### 不随机删除节点a3, cache = reg_utils.forward_propagation(X, parameters)elif keep_prob < 1:### 随机删除节点a3, cache = forward_propagation_with_dropout(X, parameters, keep_prob)else:print("keep_prob参数错误!程序退出。")exit# 计算成本## 是否使用二范数if lambd == 0:### 不使用L2正则化cost = reg_utils.compute_cost(a3, Y)else:### 使用L2正则化cost = compute_cost_with_regularization(a3, Y, parameters, lambd)# 反向传播## 可以同时使用L2正则化和随机删除节点,但是本次实验不同时使用。assert (lambd == 0 or keep_prob == 1)## 两个参数的使用情况if (lambd == 0 and keep_prob == 1):### 不使用L2正则化和不使用随机删除节点grads = reg_utils.backward_propagation(X, Y, cache)elif lambd != 0:### 使用L2正则化,不使用随机删除节点grads = backward_propagation_with_regularization(X, Y, cache, lambd)elif keep_prob < 1:### 使用随机删除节点,不使用L2正则化grads = backward_propagation_with_dropout(X, Y, cache, keep_prob)# 更新参数parameters = reg_utils.update_parameters(parameters, grads, learning_rate)# 记录并打印成本if i % 1000 == 0:## 记录成本costs.append(cost)if (print_cost and i % 10000 == 0):# 打印成本print("第" + str(i) + "次迭代,成本值为:" + str(cost))# 是否绘制成本曲线图if is_plot:plt.plot(costs)plt.ylabel('cost')plt.xlabel('iterations (x1,000)')plt.title("Learning rate =" + str(learning_rate))plt.show()# 返回学习后的参数return parameters# 进行模型学习,得到最终的参数
parameters = model(train_X, train_Y, is_plot=True)
print("训练集:")
predictions_train = reg_utils.predict(train_X, train_Y, parameters)
print("测试集:")
predictions_test = reg_utils.predict(test_X, test_Y, parameters)
运行后结果如下:
第0次迭代,成本值为:0.6557412523481002
第10000次迭代,成本值为:0.16329987525724213
第20000次迭代,成本值为:0.13851642423265018
训练集:
Accuracy: 0.9478672985781991
测试集:
Accuracy: 0.915

这样的结果看起来还算正常(因为数据集的问题,过拟合的特征还看不太出来不是很明显),接下来绘制决策边界分割曲线会看得比较明显:
plt.title("Model without regularization")
axes = plt.gca()
axes.set_xlim([-0.75, 0.40])
axes.set_ylim([-0.75, 0.65])
reg_utils.plot_decision_boundary(lambda x: reg_utils.predict_dec(parameters, x.T), train_X, train_Y)
运行结果如下:

可以很明显的看到过拟合了,钻牛角尖过分学习那几个局部特征了。
接下来试验一下引入正则化的效果。
使用L2正则化
L2正则化公式如下(L2正则化主要体现在loss的公式上面):

L2正则化成本其实就是每一层的权重的平方和,用代码np.sum(np.square(Wl))来计算。
d W [ l ] = ( f r o m b a c k p r o p ) + λ m W [ l ] , f r o m b a c k p r o p 就是 d W [ l ] dW^{[l]} =(frombackprop)+ \frac{\lambda}{m}W ^{[l]}, frombackprop就是dW^{[l]} dW[l]=(frombackprop)+mλW[l],frombackprop就是dW[l]
更新参数时, W [ l ] = W [ l ] − α d W [ l ] 更新参数时, W^{[l]} =W^{[l]} - \alpha dW ^{[l]} 更新参数时,W[l]=W[l]−αdW[l]
最终合并同类项为: W [ l ] = ( 1 − λ m ) W [ l ] − α d W [ l ] 最终合并同类项为:W^{[l]}=(1-\frac{\lambda}{m} )W^{[l]}-\alpha dW^{[l]} 最终合并同类项为:W[l]=(1−mλ)W[l]−αdW[l]
通过更新参数的公式可以看到,L2正则化是通过加入正则化参数 λ {\lambda} λ 使得网络的权重变小(重量衰减),从而削弱众多神经元的影响来解决过拟合问题。
加入如下代码,计算L2正则化的loss和反向的梯度:
def compute_cost_with_regularization(A3, Y, parameters, lambd):"""实现公式2的L2正则化计算成本参数:A3 - 正向传播的输出结果,维度为(输出节点数量,训练/测试的数量)Y - 标签向量,与数据一一对应,维度为(输出节点数量,训练/测试的数量)parameters - 包含模型学习后的参数的字典返回:cost - 使用公式2计算出来的正则化损失的值"""m = Y.shape[1]W1 = parameters["W1"]W2 = parameters["W2"]W3 = parameters["W3"]# 无正则化losscross_entropy_cost = reg_utils.compute_cost(A3, Y)# L2正则化loss,lambd*每层权重的平方和的和/(2*m)L2_regularization_cost = lambd * (np.sum(np.square(W1)) + np.sum(np.square(W2)) + np.sum(np.square(W3))) / (2 * m)cost = cross_entropy_cost + L2_regularization_costreturn cost# 当然,因为改变了成本函数,我们也必须改变向后传播的函数, 所有的梯度都必须根据这个新的成本值来计算。
def backward_propagation_with_regularization(X, Y, cache, lambd):"""实现我们添加了L2正则化的模型的后向传播。参数:X - 输入数据集,维度为(输入节点数量,数据集里面的数量)Y - 标签,维度为(输出节点数量,数据集里面的数量)cache - 来自forward_propagation()的cache输出lambda - regularization超参数,实数返回:gradients - 一个包含了每个参数、激活值和预激活值变量的梯度的字典"""m = X.shape[1](Z1, A1, W1, b1, Z2, A2, W2, b2, Z3, A3, W3, b3) = cachedZ3 = A3 - YdW3 = (1 / m) * np.dot(dZ3, A2.T) + ((lambd * W3) / m) # 前一项为frombackprop,即原来的dW3db3 = (1 / m) * np.sum(dZ3, axis=1, keepdims=True)dA2 = np.dot(W3.T, dZ3)dZ2 = np.multiply(dA2, np.int64(A2 > 0))dW2 = (1 / m) * np.dot(dZ2, A1.T) + ((lambd * W2) / m)db2 = (1 / m) * np.sum(dZ2, axis=1, keepdims=True)dA1 = np.dot(W2.T, dZ2)dZ1 = np.multiply(dA1, np.int64(A1 > 0))dW1 = (1 / m) * np.dot(dZ1, X.T) + ((lambd * W1) / m)db1 = (1 / m) * np.sum(dZ1, axis=1, keepdims=True)gradients = {"dZ3": dZ3, "dW3": dW3, "db3": db3, "dA2": dA2,"dZ2": dZ2, "dW2": dW2, "db2": db2, "dA1": dA1,"dZ1": dZ1, "dW1": dW1, "db1": db1}return gradients
调用model函数时加入lambd参数:
parameters = model(train_X, train_Y, lambd=0.7,is_plot=True)
运行代码结果如下:
第0次迭代,成本值为:0.6974484493131264
第10000次迭代,成本值为:0.2684918873282239
第20000次迭代,成本值为:0.2680916337127301
训练集:
Accuracy: 0.9383886255924171
测试集:
Accuracy: 0.93
loss走势曲线:

绘制决策边界:
这里的标题可以改一下:
plt.title("Model with L2-regularization")

可以看到训练集和测试集上的准确率几乎没有差距,或者说比无正则化的差距要小,从绘制边界可以看到没有过拟合的特征。
L2正则化会使决策边界更加平滑。但要注意,如果λ太大,也可能会“过度平滑”,从而导致模型高偏差,从而变成欠拟合的状态。
使用dropout正则化
原理是在某层当中设置保留某个神经元的概率keep-prob,在这层中随机失活1 - keep-prob概率的节点。则这层当中失活的节点在本轮迭代中的正向传播和反向传播均不参与,即失活的节点的参数在本轮训练中不作更新,没失火的节点的参数进行更新。
假设在第3层进行随机失活,在正向传播时需要进行以下三步(假设在第三层的失活):
- d3 = np.random.rand(a3.shape[0], a3.shape[1]) < keep-prob 。这句话的意思是创建一个跟a3相同shape的随机矩阵,每个值与keep-prob进行对比,小于keep-prob的为True(python计算时自动变为1),大于keep-prob即不符合的为False即0。
- a3 = np.multiply(a3, d3) 。通过和d3相乘,来失活1 - keep-prob的节点不参与计算(与0相乘为0)。
- a3 /= keep-prob 。通过缩放就在计算成本的时候仍然大致具有相同的期望值,这叫做反向dropout。
在反向传播时需要进行以下两步(假设在第三层的失活): - dA3 = dA3 * D3 。舍弃正向传播中舍弃的节点,不进行计算梯度即不进行更新。
- dA2 /= keep_prob 。进行缩放,保持大致期望。
加入以下代码进行dropout的正反向传播:
def forward_propagation_with_dropout(X, parameters, keep_prob=0.5):"""实现具有随机舍弃节点的前向传播。LINEAR -> RELU + DROPOUT -> LINEAR -> RELU + DROPOUT -> LINEAR -> SIGMOID.参数:X - 输入数据集,维度为(2,示例数)parameters - 包含参数“W1”,“b1”,“W2”,“b2”,“W3”,“b3”的python字典:W1 - 权重矩阵,维度为(20,2)b1 - 偏向量,维度为(20,1)W2 - 权重矩阵,维度为(3,20)b2 - 偏向量,维度为(3,1)W3 - 权重矩阵,维度为(1,3)b3 - 偏向量,维度为(1,1)keep_prob - 随机删除的概率,实数返回:A3 - 最后的激活值,维度为(1,1),正向传播的输出cache - 存储了一些用于计算反向传播的数值的元组"""np.random.seed(1)W1 = parameters["W1"]b1 = parameters["b1"]W2 = parameters["W2"]b2 = parameters["b2"]W3 = parameters["W3"]b3 = parameters["b3"]# LINEAR -> RELU -> LINEAR -> RELU -> LINEAR -> SIGMOIDZ1 = np.dot(W1, X) + b1A1 = reg_utils.relu(Z1)D1 = np.random.rand(A1.shape[0], A1.shape[1])D1 = D1 < keep_prob # 步骤1A1 = A1 * D1 # 步骤2A1 = A1 / keep_prob # 步骤3Z2 = np.dot(W2, A1) + b2A2 = reg_utils.relu(Z2)D2 = np.random.rand(A2.shape[0], A2.shape[1])D2 = D2 < keep_prob # 步骤1A2 = A2 * D2 # 步骤2A2 = A2 / keep_prob # 步骤3Z3 = np.dot(W3, A2) + b3A3 = reg_utils.sigmoid(Z3)cache = (Z1, D1, A1, W1, b1, Z2, D2, A2, W2, b2, Z3, A3, W3, b3)return A3, cachedef backward_propagation_with_dropout(X, Y, cache, keep_prob):"""实现我们随机删除的模型的后向传播。参数:X - 输入数据集,维度为(2,示例数)Y - 标签,维度为(输出节点数量,示例数量)cache - 来自forward_propagation_with_dropout()的cache输出keep_prob - 随机删除的概率,实数返回:gradients - 一个关于每个参数、激活值和预激活变量的梯度值的字典"""m = X.shape[1](Z1, D1, A1, W1, b1, Z2, D2, A2, W2, b2, Z3, A3, W3, b3) = cachedZ3 = A3 - YdW3 = (1 / m) * np.dot(dZ3, A2.T)db3 = 1. / m * np.sum(dZ3, axis=1, keepdims=True)dA2 = np.dot(W3.T, dZ3)dA2 = dA2 * D2 # 步骤1dA2 = dA2 / keep_prob # 步骤2dZ2 = np.multiply(dA2, np.int64(A2 > 0))dW2 = 1. / m * np.dot(dZ2, A1.T)db2 = 1. / m * np.sum(dZ2, axis=1, keepdims=True)dA1 = np.dot(W2.T, dZ2)dA1 = dA1 * D1 # 步骤1dA1 = dA1 / keep_prob # 步骤2dZ1 = np.multiply(dA1, np.int64(A1 > 0))dW1 = 1. / m * np.dot(dZ1, X.T)db1 = 1. / m * np.sum(dZ1, axis=1, keepdims=True)gradients = {"dZ3": dZ3, "dW3": dW3, "db3": db3, "dA2": dA2,"dZ2": dZ2, "dW2": dW2, "db2": db2, "dA1": dA1,"dZ1": dZ1, "dW1": dW1, "db1": db1}return gradients
调用model函数时加入keep_prob参数,设为0.86,即在每次迭代中第1层和第2层的14%的节点将不参与计算:
parameters = model(train_X, train_Y, keep_prob=0.86, learning_rate=0.3,is_plot=True)
运行代码结果如下:
第10000次迭代,成本值为:0.061016986574905605
第20000次迭代,成本值为:0.060582435798513114
训练集:
Accuracy: 0.9289099526066351
测试集:
Accuracy: 0.95

这里的标题可以改一下:
plt.title("Model with dropout")

可以看到使用dropout让训练集的准确率稍微降低了些,但测试集上的准确率提升了,提高了泛化能力,还是很成功的。
dropout防止过拟合的原因:每个神经元都不依赖于任何特征,因为任意一个特征都有可能被清除。
注意,测试阶段不使用dropout,因为要保证测试结果的稳定。
相关文章:

正则化解决过拟合
本片举三个例子进行对比,分别是:不使用正则化、使用L2正则化、使用dropout正则化。 首先是前后向传播、加载数据、画图所需要的相关函数的reg_utils.py: # -*- coding: utf-8 -*-import numpy as np import matplotlib.pyplot as plt impor…...

在 Windows 上安装 Helm包
一、前言 个人主页: ζ小菜鸡大家好我是ζ小菜鸡,让我们一起学习在 Windows 上安装 Helm包。如果文章对你有帮助、欢迎关注、点赞、收藏(一键三连) 二、 Helm是什么 Helm是Kubernetes的包管理工具,类似于centos的yum,能够快速查找、下载和安装…...
Clion开发STM32之OTA升级模块(一)
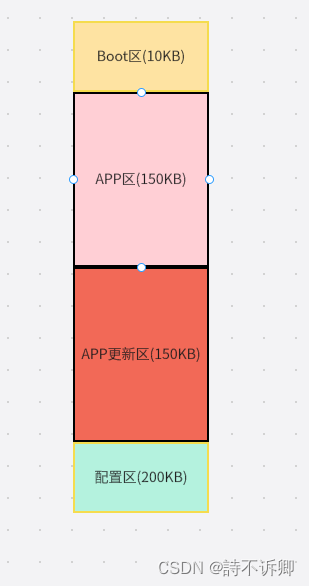
什么是OTA 百度百科解释个人理解:就是不通过烧录的方式,通过串口、网口、无线对主板运行的程序进行升级。减少后期的一个维护迭代程序的一个成本。 STM32的OTA升级模块的一个设计 程序启动的一个框架流程图(大致流程) FLASH的一个划分框图 BootLoader…...

Java供应链安全检测SDL方法论
近些年,开源程序陆续爆出安全漏洞,轻则影响用户体验,重则业务应用沦陷。大量的业务应用以及每天数千次的迭代,使得自动检测和治理第三方开源程序成为企业安全建设的必要一环。如何来建设这一环呢?SCA(软件成分分析) 概念 什么是SCA? 源代码或二进制扫描的软件成分分析 什…...
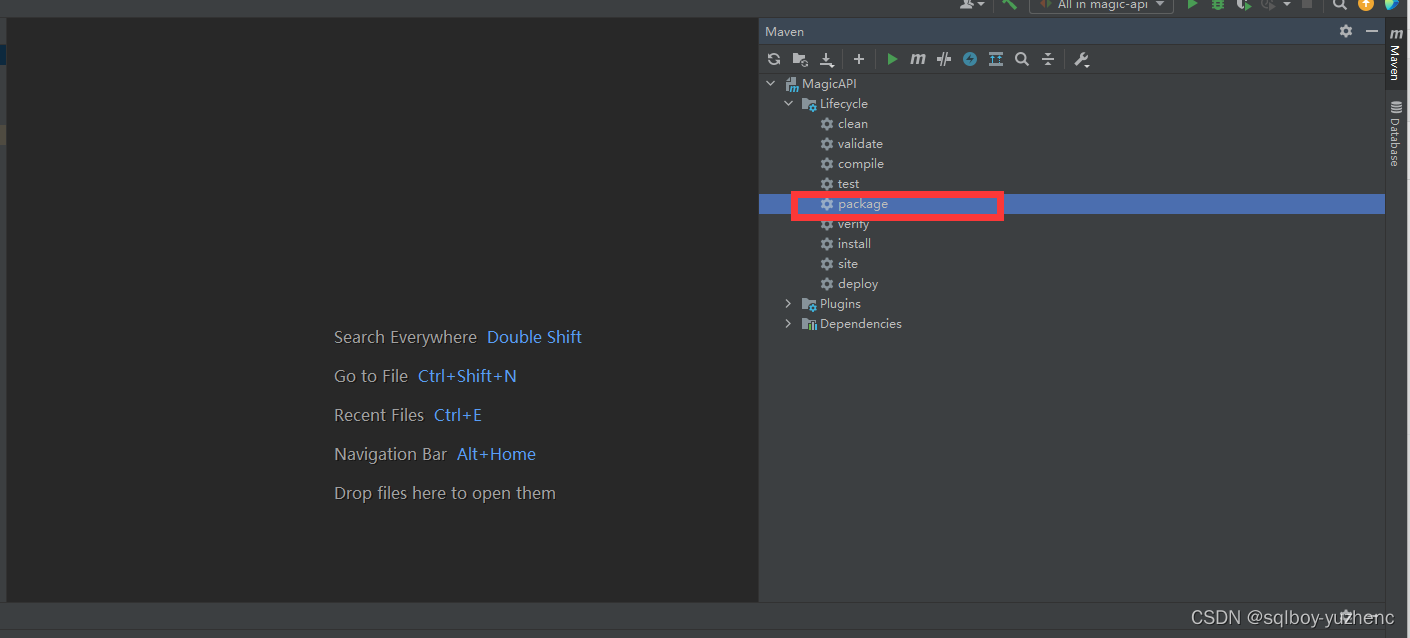
Magic-API的部署
目录 概述简介特性 搭建创建元数据表idea新建spring-boot项目pom.xmlapplication.properties打包上传MagicAPI-0.0.1-SNAPSHOT.jar开启服务访问 magic语法 概述 简介 magic-api是一个基于Java的接口快速开发框架,编写接口将通过magic-api提供的UI界面完成…...
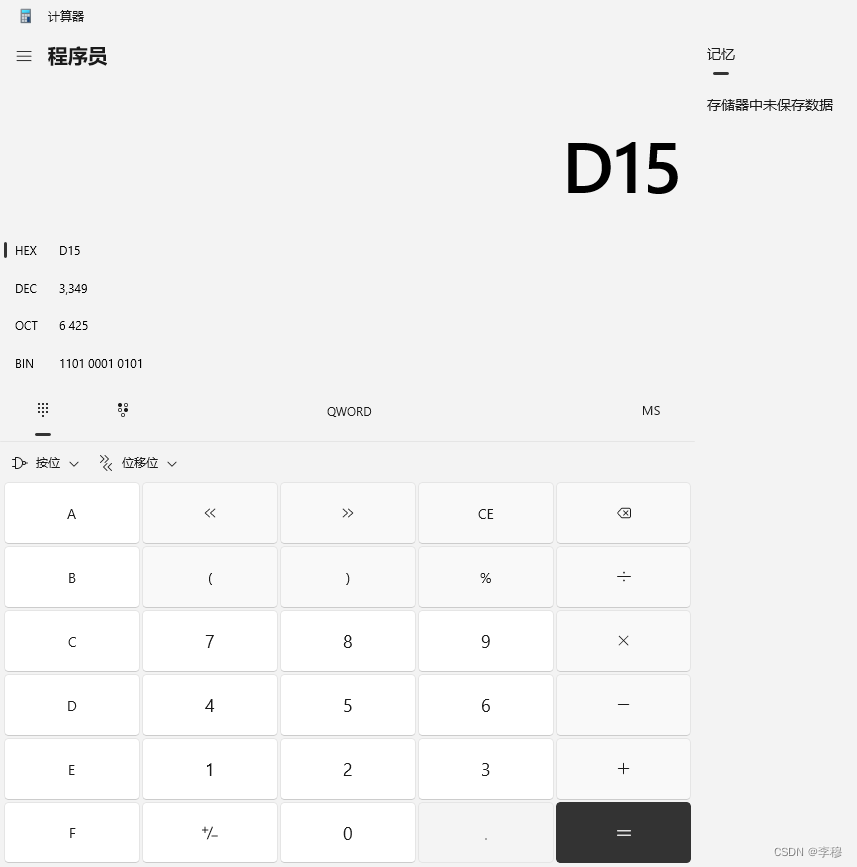
程序进制换算
进制数介绍 一、进制介绍 二进制 :0或1,满2进1,以0B或者0b开头,如 0b1101 八进制:0-7,满8进1,,以0开头,如0234 十进制:0-9,满10进1,…...

Packet Tracer - 使用 CLI 配置并验证站点间 IPsec VPN
Packet Tracer - 使用 CLI 配置并验证站点间 IPsec VPN 地址分配表 设备 接口 IP 地址 子网掩码...
100%通过率 超详细代码注释 代码解读)
【华为OD机试真题】最小的调整次数(python版)100%通过率 超详细代码注释 代码解读
【华为OD机试真题 2022&2023】真题目录 @点这里@ 【华为OD机试真题】信号发射和接收 &试读& @点这里@ 【华为OD机试真题】租车骑绿道 &试读& @点这里@ 最小的调整次数 知识点队列栈 时间限制:1s空间限制:256MB限定语言:不限 题目描述: 有一个特异性…...
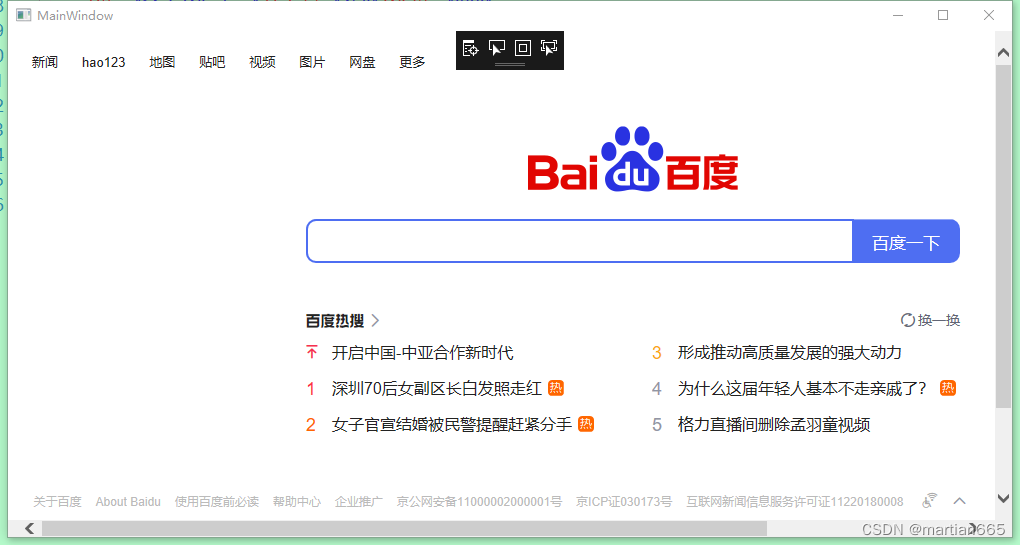
WPF中嵌入web网页控件 WebBrowser
1 WebBrowser特点 <font colorblue>WebBrowser控件内部使用IE的引擎,因此使用WebBrowser我们必须安装IE浏览器。 WebBrowser使用的是IE内核,许多H5新特性都不支持,然后使用谷歌内核和火狐内核会使软件的体积增加至几十MB。 <font c…...
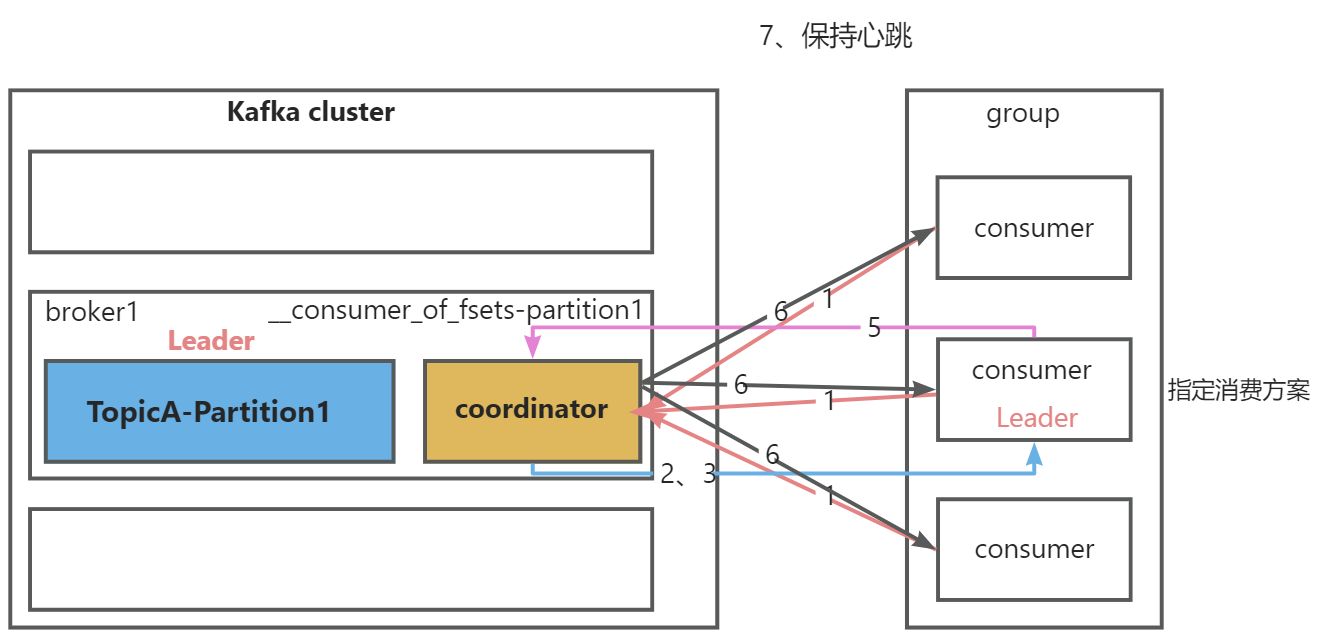
Kafka原理之消费者
一、消费模式 1、pull(拉)模式(kafka采用这种方式) consumer采用从broker中主动拉取数据。 存在问题:如果kafka中没有数据,消费者可能会陷入循环中,一直返回空数据 2、push(推)模式 由broker决定消息发送频率,很难适应所有消费者…...
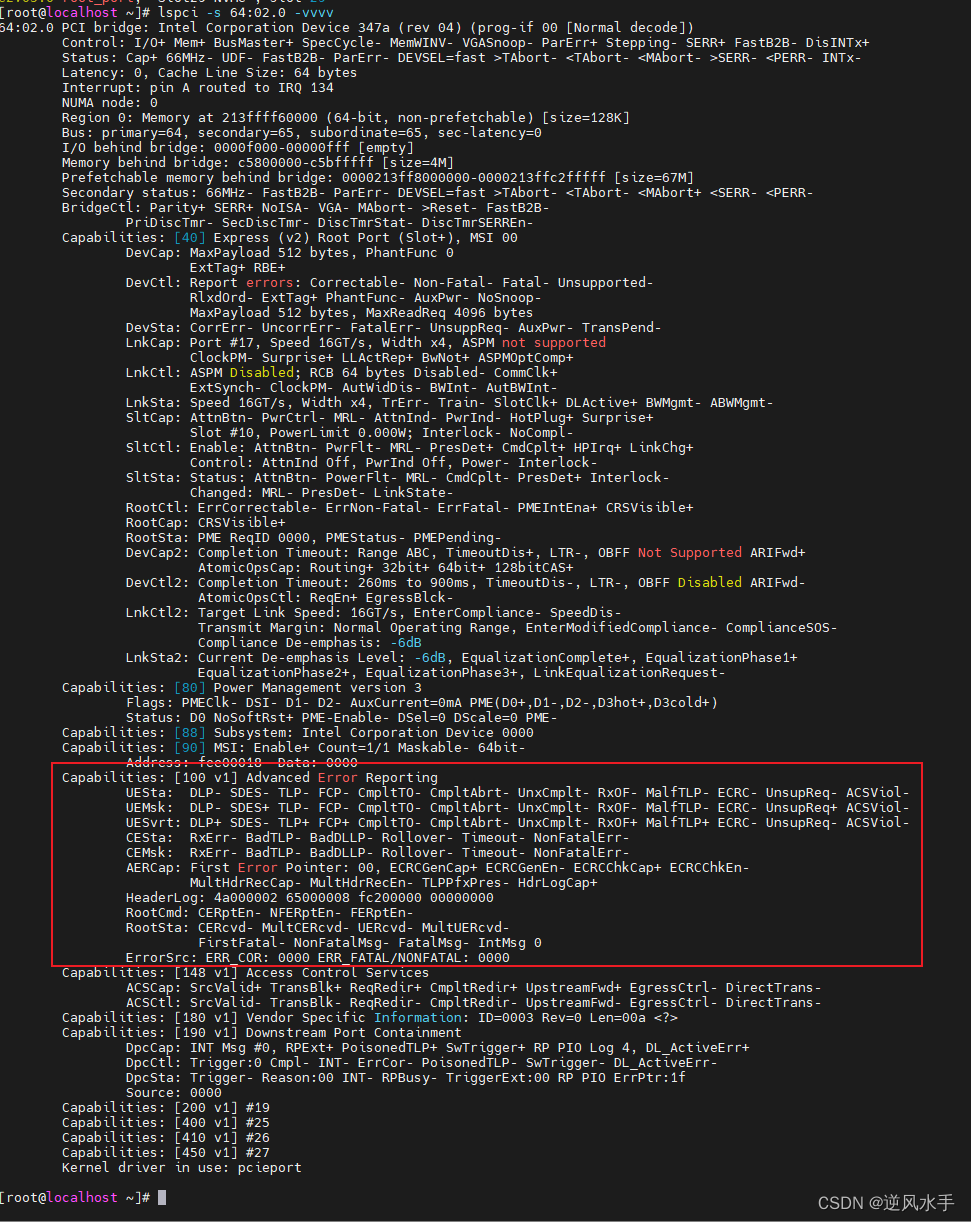
PCIe的capability扩展空间字段解释
解释 这是一段关于高级错误报告的信息,其中包含多个字段和值。以下是每个字段的详细解释: Capabilities: [100 v1] Advanced Error Reporting 这是该设备支持高级错误报告的能力标识符。 UESta: DLP- SDES- TLP- FCP- CmpltTO- CmpltAbrt- UnxCmplt- R…...

力扣sql中等篇练习(二十)
力扣sql中等篇练习(二十) 1 寻找面试候选人 1.1 题目内容 1.1.1 基本题目信息1 1.1.2 基本题目信息2 1.1.3 示例输入输出 a 示例输入 b 示例输出 1.2 示例sql语句 # 分为以下两者情况,分别考虑,然后union进行处理(有可能同时满足,需要去进行去重) # ①该用户在 三场及更多…...
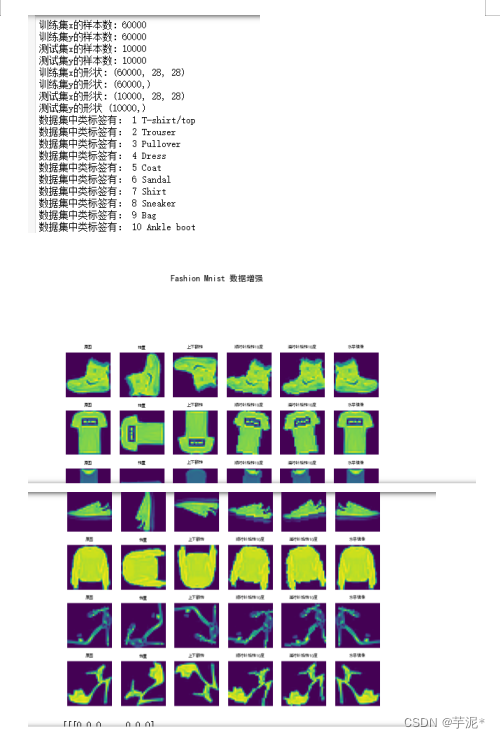
【神经网络】tensorflow -- 期中测试试题
题目一:(20分) 请使用Matplotlib中的折线图工具,绘制正弦和余弦函数图像,其中x的取值范围是,效果如图1所示。 要求: (1)正弦图像是蓝色曲线,余弦图像是红色曲线,线条宽度…...

计算机基础--计算机存储单位
一、介绍 计算机中表示文件大小、数据载体的存储容量或进程的数据消耗的信息单位。在计算机内部,信息都是釆用二进制的形式进行存储、运算、处理和传输的。信息存储单位有位、字节和字等几种。各种存储设备存储容量单位有KB、MB、GB和TB等几种。 二、基本存储单元…...

大数据Doris(十六):分桶Bucket和分区、分桶数量和数据量的建议
文章目录 分桶Bucket和分区、分桶数量和数据量的建议 一、分桶Bucket...

【webrtc】web端打开日志及调试
参考gist Chrome Browser debug logs sawbuck webrtc-org/native-code/logging 取日志 C:\Users\zhangbin\AppData\Local\Google\Chrome\User Data C:\Users\zhangbin\AppData\Local\Google\Chrome\User Data\chrome_debug.logexe /c/Program Files/Google/Chrome/Applicationz…...
)
C++ Primer第五版_第十六章习题答案(61~67)
文章目录 练习16.61练习16.62Sales_data.hex62.cpp 练习16.63练习16.64练习16.65练习16.66练习16.67 练习16.61 定义你自己版本的 make_shared。 template <typename T, typename ... Args> auto make_shared(Args&&... args) -> std::shared_ptr<T> {r…...

python定时任务2_celery flower计划任务
启动worker: celery -A tasks worker --loglevelerror --poolsolo worker启动成功 启动beat celery -A tasks beat --loglevelinfo beat启动成功 启动flower celery -A tasks flower --loglevelinfo flower启动成功,然后进入http://localhost:5555 可…...

地狱级的字节跳动面试,6年测开的我被按在地上摩擦.....
前几天我朋友跟我吐苦水,这波面试又把他打击到了,做了快6年软件测试员。。。为了进大厂,也花了很多时间和精力在面试准备上,也刷了很多题。但题刷多了之后有点怀疑人生,不知道刷的这些题在之后的工作中能不能用到&…...
怎么开发外贸网站
随着全球经济的发展,越来越多的企业选择走上国际化的道路,开展国际贸易业务。而外贸网站是一个相对常见的开展国际贸易业务的平台。那么,如何开发一款优秀的外贸网站呢? 首先,我们需要明确外贸网站的目标用户群体。由…...

LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器的上位机配置操作说明
LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器专为工业环境精心打造,完美适配AGV和无人叉车。同时,集成以太网与语音合成技术,为各类高级系统(如MES、调度系统、库位管理、立库等)提供高效便捷的语音交互体验。 L…...

【Python】 -- 趣味代码 - 小恐龙游戏
文章目录 文章目录 00 小恐龙游戏程序设计框架代码结构和功能游戏流程总结01 小恐龙游戏程序设计02 百度网盘地址00 小恐龙游戏程序设计框架 这段代码是一个基于 Pygame 的简易跑酷游戏的完整实现,玩家控制一个角色(龙)躲避障碍物(仙人掌和乌鸦)。以下是代码的详细介绍:…...

使用VSCode开发Django指南
使用VSCode开发Django指南 一、概述 Django 是一个高级 Python 框架,专为快速、安全和可扩展的 Web 开发而设计。Django 包含对 URL 路由、页面模板和数据处理的丰富支持。 本文将创建一个简单的 Django 应用,其中包含三个使用通用基本模板的页面。在此…...

docker详细操作--未完待续
docker介绍 docker官网: Docker:加速容器应用程序开发 harbor官网:Harbor - Harbor 中文 使用docker加速器: Docker镜像极速下载服务 - 毫秒镜像 是什么 Docker 是一种开源的容器化平台,用于将应用程序及其依赖项(如库、运行时环…...

day52 ResNet18 CBAM
在深度学习的旅程中,我们不断探索如何提升模型的性能。今天,我将分享我在 ResNet18 模型中插入 CBAM(Convolutional Block Attention Module)模块,并采用分阶段微调策略的实践过程。通过这个过程,我不仅提升…...

YSYX学习记录(八)
C语言,练习0: 先创建一个文件夹,我用的是物理机: 安装build-essential 练习1: 我注释掉了 #include <stdio.h> 出现下面错误 在你的文本编辑器中打开ex1文件,随机修改或删除一部分,之后…...

蓝牙 BLE 扫描面试题大全(2):进阶面试题与实战演练
前文覆盖了 BLE 扫描的基础概念与经典问题蓝牙 BLE 扫描面试题大全(1):从基础到实战的深度解析-CSDN博客,但实际面试中,企业更关注候选人对复杂场景的应对能力(如多设备并发扫描、低功耗与高发现率的平衡)和前沿技术的…...

如何在看板中有效管理突发紧急任务
在看板中有效管理突发紧急任务需要:设立专门的紧急任务通道、重新调整任务优先级、保持适度的WIP(Work-in-Progress)弹性、优化任务处理流程、提高团队应对突发情况的敏捷性。其中,设立专门的紧急任务通道尤为重要,这能…...

什么?连接服务器也能可视化显示界面?:基于X11 Forwarding + CentOS + MobaXterm实战指南
文章目录 什么是X11?环境准备实战步骤1️⃣ 服务器端配置(CentOS)2️⃣ 客户端配置(MobaXterm)3️⃣ 验证X11 Forwarding4️⃣ 运行自定义GUI程序(Python示例)5️⃣ 成功效果
人工智能(大型语言模型 LLMs)对不同学科的影响以及由此产生的新学习方式
今天是关于AI如何在教学中增强学生的学习体验,我把重要信息标红了。人文学科的价值被低估了 ⬇️ 转型与必要性 人工智能正在深刻地改变教育,这并非炒作,而是已经发生的巨大变革。教育机构和教育者不能忽视它,试图简单地禁止学生使…...
