并查集算法
文章目录
- 1. 原理介绍
- 2. 并查集的应用
- 3. find()函数的定义与实现
- 4. 并查集的join函数
- 5. 路径压缩优化算法-优化find
- 6. 路径压缩优化算法+按秩合并算法
1. 原理介绍
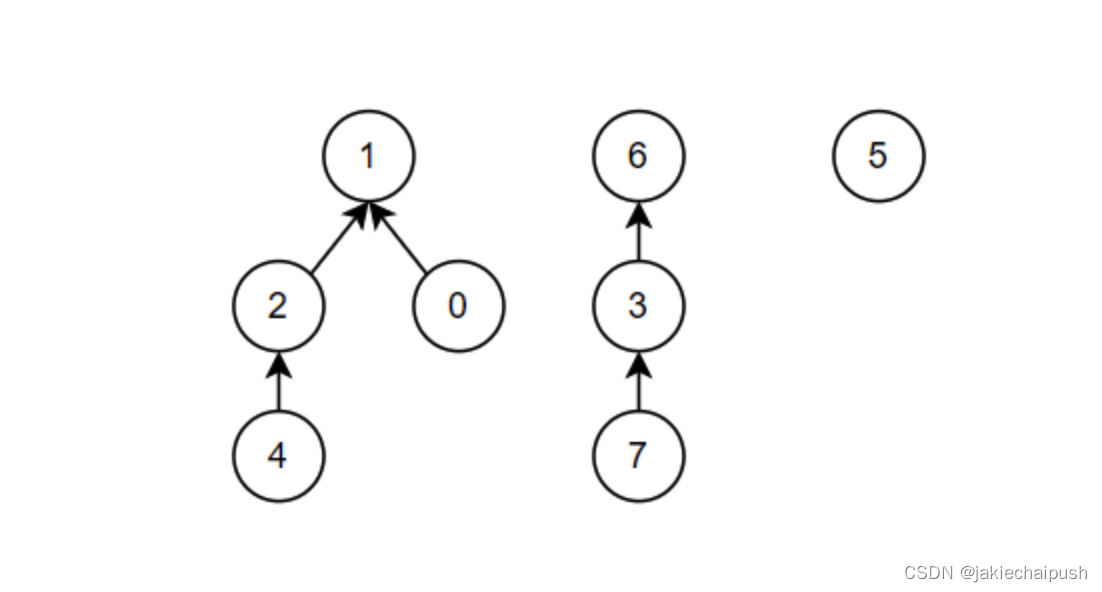
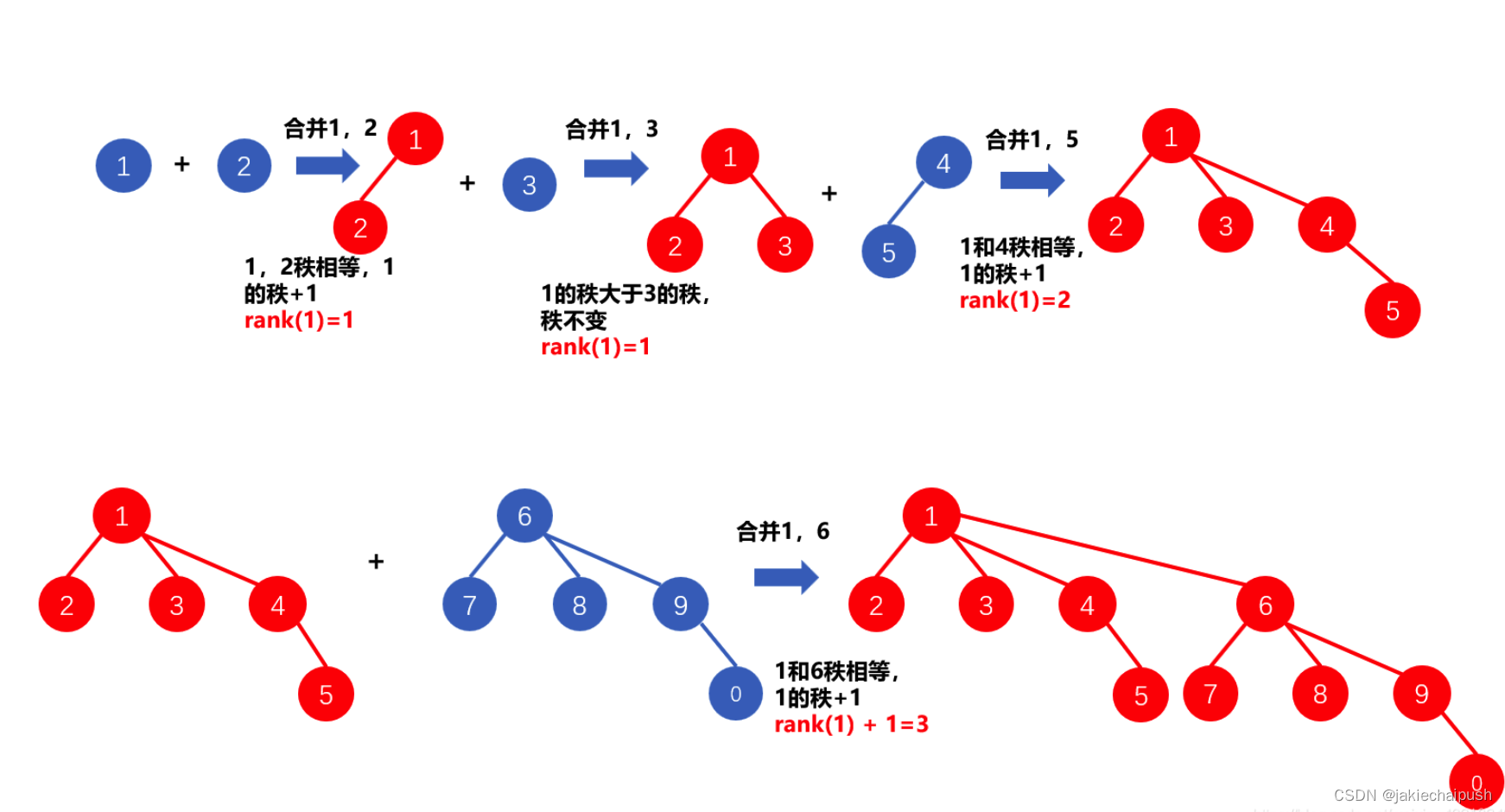
并查集是一种用于维护集合关系的数据结构,它支持合并集合和查询元素所在的集合。它的基本思想是将元素分组,每个组称为一个集合,最终目的是实现高效地判断两个元素是否在同一集合中。并查集维护的是一棵树,其中每个节点代表一个元素,节点之间的边表示它们属于同一个集合。初始时,每个元素都是一个独立的集合,也就是一棵只有一个节点的树。合并两个集合时,只需要将其中一个集合的根节点挂在另一个集合的根节点下面即可。查询元素所在的集合时,只需要一直向上找到根节点即可。并查集的时间复杂度取决于路径压缩和按秩合并这两种优化策略。路径压缩是指在查询根节点的过程中,将路径上的所有节点都直接挂在根节点下面,以减少下次查询的时间。按秩合并是指在合并两个集合的时候,将元素个数少的集合挂在元素个数多的集合下面,以保持树的平衡性。
2. 并查集的应用
并查集常用于解决图论中的连通性问题,例如判断无向图是否连通,求图的最小生成树等。另外,它还可以用于离散化处理等场景。
3. find()函数的定义与实现
前面在介绍原理的时候说到,并查集的基本思想是将元素分组,每个组称为一个集合,最终目的是实现高效地判断两个元素是否在同一个集合中。而find函数的作用就是判断一个元素是否属于一个组,而所谓的一组实际上就是一棵树。那么find函数是如何实现判断一个元素是否属于一个组的?原理其实很简单,其实每个组都会有个代表元(这个代表元通常是更节点),只要两个元素拥有共同的代表元它们就属于同一个组。下面我们基于代码分析一下,find函数的原理:
public int find(int x) {while (parent[x] != x) {x = parent[x];}return x;
}
在该实现中,我们使用一个while循环来一直向上查找,直到找到该元素所在组的根节点为止。在查找的过程中,我们每次都将当前元素的父节点(parent[x])作为下一个元素进行查找。当找到根节点时,循环终止,返回该节点即可。然而,当并查集的规模比较大时,这种实现的时间复杂度会很高,为 O ( n ) O(n) O(n),其中 n n n是并查集中元素的总数。而优化后的实现可以将时间复杂度降低到 O ( α ( n ) ) O(\alpha(n)) O(α(n)),其中 α \alpha α是阿克曼函数的反函数,可以认为它是一个极小的值,因此可以近似地看作是常数时间复杂度。因此,路径压缩优化对于并查集的性能提升非常显著。
4. 并查集的join函数
并查集(Union-Find Set)中的 join() 函数用于将两个元素所在的组合并成一个大组,它的实现原理很简单,即将其中一个元素的根节点指向另一个元素的根节点即可。具体来说,它的实现可以分为以下两个步骤:
-
找到两个元素所在组的根节点。我们可以使用并查集中的 find() 函数来查找两个元素所在组的根节点。如果它们的根节点相同,则说明它们已经在同一个组中,不需要再合并了。
-
合并两个组。如果两个元素不在同一个组中,则需要将它们所在的组合并成一个大组。具体来说,我们可以将其中一个元素的根节点指向另一个元素的根节点,从而将两个组合并成一个大组。
以下是并查集中 join() 函数的 Java 代码实现:
public void join(int x, int y) {int rootX = find(x);int rootY = find(y);if (rootX != rootY) {parent[rootX] = rootY;}
}
其中,parent 是一个数组,用于存储每个元素所在组的根节点。初始时,每个元素的父节点都是它自己,即 parent[i] = i。在 join() 函数中,我们首先使用 find() 函数来找到 x 和 y 所在组的根节点。如果它们的根节点相同,说明它们已经在同一个组中,不需要再合并了。如果它们的根节点不同,说明它们不在同一个组中,需要将它们所在的组合并成一个大组。为了实现这一点,我们将其中一个元素的根节点指向另一个元素的根节点即可,这里我们选择将 x 所在组的根节点 rootX 指向 y 所在组的根节点 rootY。具体来说,我们可以将 parent[rootX] 的值赋为 rootY,从而将 x 所在组的所有元素的根节点都指向 y 所在组的根节点 rootY,从而将两个组合并成一个大组。需要注意的是,这里的 join() 函数只是简单地将其中一个元素的根节点指向另一个元素的根节点,并不考虑各组的大小和深度等因素,因此可能会导致并查集出现深度不平衡的情况。针对这个问题,可以使用一些其他的优化策略,例如按秩合并和路径压缩等,以提高并查集的性能和稳定性。
5. 路径压缩优化算法-优化find
前面我们说到,原始的find函数的查找根节点的时间复杂度较高,这里我们考虑将其进行优化。路径压缩是并查集中一种常用的优化技术,它通过修改树的结构来减少后续查找所需经过的节点数量,从而提高并查集的性能。在并查集中,每个元素都有一个父节点,用于表示它所在的组的根节点。当我们查找一个元素所在的组时,实际上就是在不断向上查找该元素的父节点,直到找到根节点为止。路径压缩就是在这个查找的过程中,将沿途经过的所有节点的父节点直接指向根节点,从而降低后续查找所需经过的节点数量。
具体来说,路径压缩的原理可以分为两个步骤:
-
查找根节点:我们首先使用递归调用的方式,不断查找当前元素的父节点,直到找到根节点为止。在查找过程中,如果当前元素的父节点不是根节点,那么我们就将其父节点设置为下一次查找的元素。
-
路径压缩:当我们找到根节点后,就会得到整个树的结构。此时,为了减少后续查找所需经过的节点数量,我们可以将沿途经过的所有节点的父节点都直接指向根节点。这个过程可以在递归调用的返回过程中完成,具体来说就是在返回前将当前元素的父节点设置为根节点即可。
以下是基于路径压缩优化的并查集中find()函数的Java实现:
public int find(int x) {if (parent[x] != x) {parent[x] = find(parent[x]); // 路径压缩}return parent[x];
}6. 路径压缩优化算法+按秩合并算法
路径压缩算法还可以与按秩合并算法结合起来,以进一步提高并查集的性能和稳定性。具体来说,可以在每个节点上增加一个权值,表示该节点所在组的大小或深度等信息,从而实现按秩合并算法的功能。在进行路径压缩的同时,还可以更新节点的权值信息,从而保证并查集的平衡性和稳定性。在路径压缩算法中,为了避免对并查集中所有节点都进行路径压缩操作,可能会出现一些节点的父节点指向了自己的情况。为了避免这种情况,可以在进行路径压缩时,同时对节点进行加权标记,表示该节点已经进行了路径压缩操作。具体来说,可以在 find() 函数中增加一个参数 compress,表示是否进行路径压缩,同时在每个节点上增加一个标记 compressed,表示该节点是否已经进行了路径压缩。修改后的 find() 函数实现如下:
public int find(int x, boolean compress) {if (parent[x] != x) {if (compress && !compressed[x]) {// 路径压缩,并更新节点的权值信息parent[x] = find(parent[x], compress);size[x] = size[parent[x]];compressed[x] = true;} else {// 递归查找根节点parent[x] = find(parent[x], compress);}}return parent[x];
}
相关文章:

并查集算法
文章目录 1. 原理介绍2. 并查集的应用3. find()函数的定义与实现4. 并查集的join函数5. 路径压缩优化算法-优化find6. 路径压缩优化算法按秩合并算法 1. 原理介绍 并查集是一种用于维护集合关系的数据结构,它支持合并集合和查询元素所在的集合。它的基本思想是将元…...
十分钟在 macOS 快速搭建 Linux C/C++ 开发环境
有一个使用了 Epoll 的 C 项目,笔者平时用的 Linux 主力开发机不在身边,想在 macOS 上开发调试,但是没有 Linux 虚拟机。恰好,JetBrains CLion 的 Toolchains 配置除了使用本地环境,还支持 SSH、Docker。 笔者使用 CL…...
银河麒麟系统Arm64编译opencv指南
进入opencv官网下载版本;我这边下载的是2.4.13.6 ;根据需要下载最新的 Releases - OpenCV 拷贝进麒麟系统我这边是麒麟V10 sp1 2204;并解 cmake 在麒麟应用商城中安装; 打开cmake 设置opencv路径;builder文件夹可以自…...

蒙层禁止下方页面滚动防抖动完美方案
学习链接 js如何禁止滚动条滚动,但不消失! - 这个是完美解决方案(在线demo示例) 解决窗口滚动条消失而导致的页面内容抖动的问题 完美解决js 禁止滚动条滚动,并且滚动条不消失,页面大小不闪动 蒙层禁止…...

微积分python基础
微积分基础(python) 文章目录 微积分基础(python)1 函数与极限2 求导与微分3 不定积分4 定积分 1 函数与极限 # 导入sympy库 from sympy import * # 将x符号化 x Symbol("x") xx \displaystyle x x # 利用sympy中solve函数求解方程 X solve(x**2-10*x21,x) X pri…...
)
Redis缓存数据库(一)
目录 一、概述 1、Redis 2、Redis的安装 Redis Windows环境设置 3、String: 字符串 3.1、字符串 3.2、数值 3.3、bitmap 4、Hash: 散列 5、List: 列表 6、Set: 集合 7、Sorted Set: 有序集合 一、概述 常识: 磁盘:1.寻址:ms&…...

物联网|uart串口相关寄存器|波特率设置及计算|发送处理代码|串口接收中断处理函数|物联网之蓝牙4.0 BLE基础-学习笔记(7)
文章目录 13 uart串口基础开发基本电路图:实验相关寄存器波特率设置及计算计算过程:设置中断发送处理代码串口接收中断处理函数main.c 13 uart串口基础开发 基本电路图: 实验相关寄存器 相关寄存器UxCSR、UxCSR、UxGCR、UxBUF、UxBAUD、CLK…...

有数·智享未来 | 新华三重磅发布绿洲平台3.0
5月10日,紫光股份旗下新华三集团以“有数智享未来”为主题,成功举办绿洲平台3.0新品发布会。全新一代绿洲平台实现内核进阶,以五大技术能力升级、五大行业方案沉淀、六类服务能力保障,三位一体构筑更领先的用数底座、更落地的用数…...
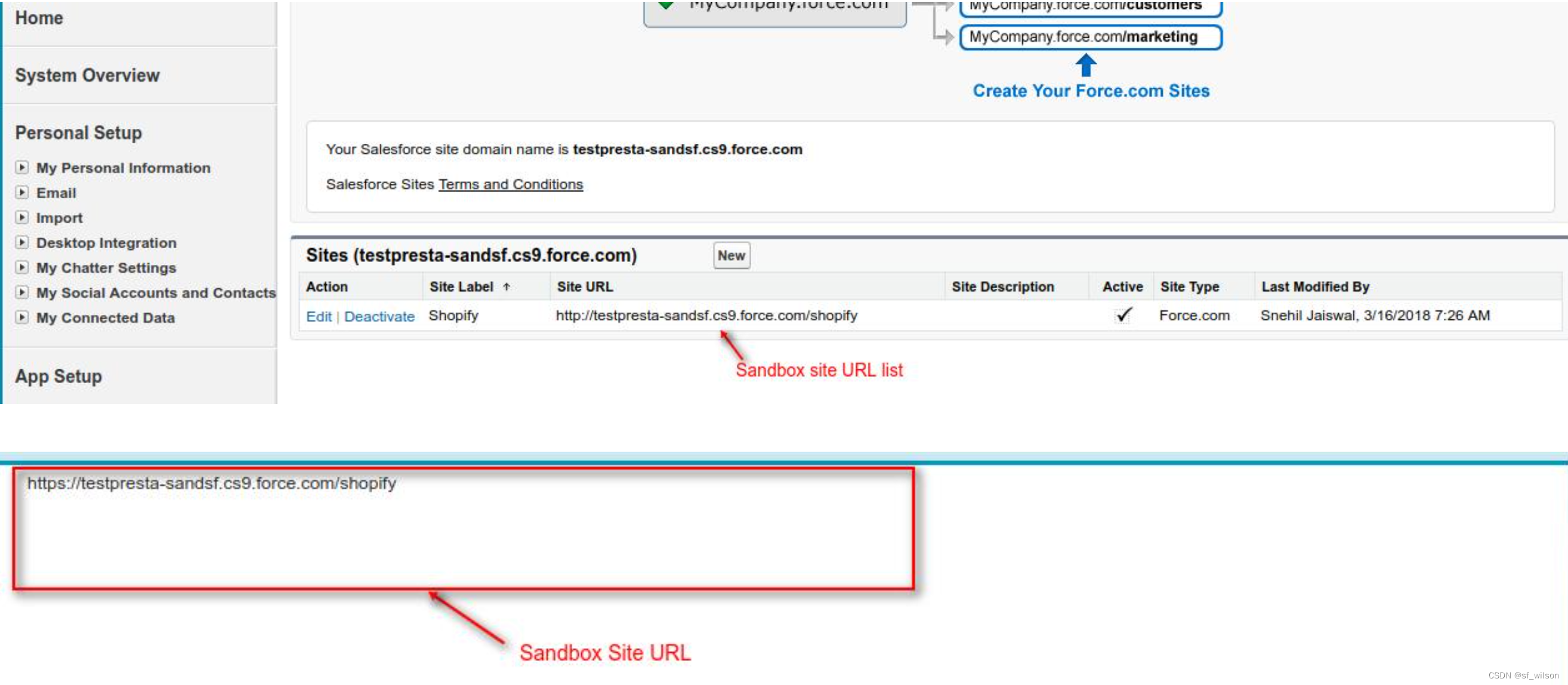
在Apex中获取Site URL
Foreword 目前SF暂未提供直接有效的方法在Apex获取SiteURL,我们可以在Idea (Access URL for a Site or Community from Apex)页面投票,除了下面提供的一种hack思路,当然也可以通过Custom Label手动维护。 Format of Site URL Sandbox site …...
【电子学会】2023年03月图形化三级 -- 比大小.md
文章目录 比大小1. 准备工作2. 功能实现3. 设计思路与实现(1)角色分析(2)背景分析(3)所用积木块介绍a. 运动类b. 外观类c. 事件类d. 控制类e. 运算类f. 变量类 (4)角色、舞台背景设置…...
Kali-linux使用Nessus
Nessus号称是世界上最流行的漏洞扫描程序,全世界有超过75000个组织在使用它。该工具提供完整的电脑漏洞扫描服务,并随时更新其漏洞数据库。Nessus不同于传统的漏洞扫描软件,Nessus可同时在本机或远端上遥控,进行系统的漏洞分析扫描…...

青训营 x 训练营结营测试题目(前端方向)
文章目录 📋前言🎯选择题(含多选)📝最后 📋前言 这篇文章的内容是23年6月青训营 x 训练营结营题目,题目一共有25题,题目类型为选择题,包括了单选题和多选题,…...
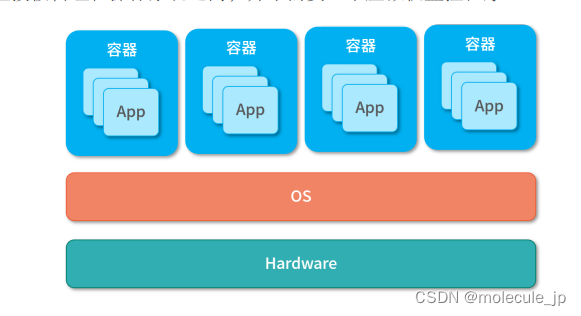
虚拟化技术介绍-VMware和Docker的区别
都说今天是一个云时代,其实云的本质就是由基础架构提供商提供基础架构,应用开发商不再关心基础架构。我们可以类比人类刚刚发明电的时候,工厂需要自己建电站,而现在只需要电线和插座就可以使用电。云时代让我们可以在分钟、甚至秒…...
TinyHttpd 运行过程出现的问题
最近拉了个 TinyHttpd 的工程下来,不过好像各个都有些改动,最后挑了篇阅读量最多的。工程也是从这里面给的链接下载的。 参考自:https://blog.csdn.net/jcjc918/article/details/42129311 拿下来在编译运行前,按这里说的&#x…...
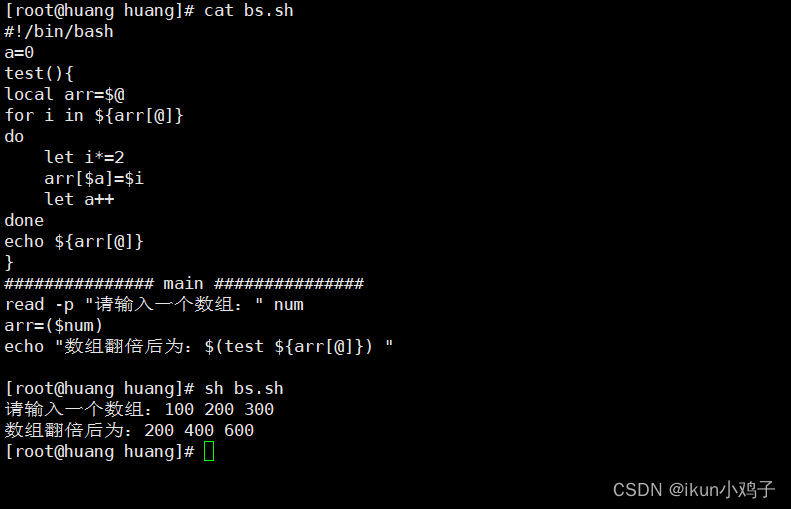
【Linux】shell编程—数组
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 一、shell数组1,数组的概念2.数组的定义 二、Shell数组操作1. 获取数组的所有元素的列表2. 获取数组的所有元素下标3.取数组的元素个数4. 获取数组的某个元素的值5.…...

Maven仓库与Maven插件
目录 Maven 仓库 本地仓库 中央仓库 远程仓库 Maven 依赖搜索顺序 Maven 阿里云(Aliyun)仓库 gradle 配置指南 Maven 插件 插件类型 实例 Maven 仓库 在 Maven 的术语中,仓库是一个位置(place)。 Maven 仓库是项目中依赖的第三方库…...
【溯源反制】CDN域前置云函数-流量分析|溯源
文章目录 CDN隐藏C2地址环境搭建上传至威胁感知平台直接分析使用DNSQuerySniffer和Process Monitor定位进程网络流量分析文件属性(IDAPro Ollydbg) 域前置隐藏环境搭建威胁感知流量分析 云服务API网关/云函数云函数使用HTTPcs的流量可以简单的分为三个阶段 云函数使用HTTPS 总结…...

【Vue】学习笔记-全局事件总线
全局事件总线(GlobalEventBus) 一种可以在任意组件通信的方式,本质上就是一个对象,它必须满足以下条件 所有的组件对象都必须能看见他这个对象必须能够使用$ on $ emit $ off方法取绑定、触发和解绑事件 使用步骤 定义全局事件总线 //创建VUE new V…...

MATLAB数值运算(六)
目录 实验目的 实验内容 原创代码,仅供参考,不要直接CV呀 ~_~ 实验目的 1)掌握定义符号对象和创建符号表达式的方法; 2)掌握符号运算基本命令和规则; 3)掌握符号表达式的运算法则以及符号矩阵…...

某医院Pad网络故障分析
分析背景 某医院为了加强信息安全管理,防止病人隐私信息泄露,采用部署“零信任”安全架构设计理念的企业移动安全支撑平台方案。 但在部署前期测试时,遇到了严重的性能问题。 在本次测试环境中,通过PAD访问患者转运业务&#x…...

【Axure高保真原型】引导弹窗
今天和大家中分享引导弹窗的原型模板,载入页面后,会显示引导弹窗,适用于引导用户使用页面,点击完成后,会显示下一个引导弹窗,直至最后一个引导弹窗完成后进入首页。具体效果可以点击下方视频观看或打开下方…...

Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以?
Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以? 在 Golang 的面试中,map 类型的使用是一个常见的考点,其中对 key 类型的合法性 是一道常被提及的基础却很容易被忽视的问题。本文将带你深入理解 Golang 中…...

基础测试工具使用经验
背景 vtune,perf, nsight system等基础测试工具,都是用过的,但是没有记录,都逐渐忘了。所以写这篇博客总结记录一下,只要以后发现新的用法,就记得来编辑补充一下 perf 比较基础的用法: 先改这…...

uniapp微信小程序视频实时流+pc端预览方案
方案类型技术实现是否免费优点缺点适用场景延迟范围开发复杂度WebSocket图片帧定时拍照Base64传输✅ 完全免费无需服务器 纯前端实现高延迟高流量 帧率极低个人demo测试 超低频监控500ms-2s⭐⭐RTMP推流TRTC/即构SDK推流❌ 付费方案 (部分有免费额度&#x…...

C++ 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

ip子接口配置及删除
配置永久生效的子接口,2个IP 都可以登录你这一台服务器。重启不失效。 永久的 [应用] vi /etc/sysconfig/network-scripts/ifcfg-eth0修改文件内内容 TYPE"Ethernet" BOOTPROTO"none" NAME"eth0" DEVICE"eth0" ONBOOT&q…...

【分享】推荐一些办公小工具
1、PDF 在线转换 https://smallpdf.com/cn/pdf-tools 推荐理由:大部分的转换软件需要收费,要么功能不齐全,而开会员又用不了几次浪费钱,借用别人的又不安全。 这个网站它不需要登录或下载安装。而且提供的免费功能就能满足日常…...
详细解析)
Caliper 负载(Workload)详细解析
Caliper 负载(Workload)详细解析 负载(Workload)是 Caliper 性能测试的核心部分,它定义了测试期间要执行的具体合约调用行为和交易模式。下面我将全面深入地讲解负载的各个方面。 一、负载模块基本结构 一个典型的负载模块(如 workload.js)包含以下基本结构: use strict;/…...

群晖NAS如何在虚拟机创建飞牛NAS
套件中心下载安装Virtual Machine Manager 创建虚拟机 配置虚拟机 飞牛官网下载 https://iso.liveupdate.fnnas.com/x86_64/trim/fnos-0.9.2-863.iso 群晖NAS如何在虚拟机创建飞牛NAS - 个人信息分享...

【深度学习新浪潮】什么是credit assignment problem?
Credit Assignment Problem(信用分配问题) 是机器学习,尤其是强化学习(RL)中的核心挑战之一,指的是如何将最终的奖励或惩罚准确地分配给导致该结果的各个中间动作或决策。在序列决策任务中,智能体执行一系列动作后获得一个最终奖励,但每个动作对最终结果的贡献程度往往…...
