随机变量X,分布函数X~F(x)的理解。
1.随机变量X
1.通常认知的"x"与随机变量X
我们通常意义上的 x 是自变量,y = f(x) 中的自变量。
但是 X 更多意义是 对应法则 " f " ,X完整写法是 X(ω) ω ∈ Ω。
X这个对应法则,可以将样本点映射到实数轴上。
那么X这个对应法则到底是什么,又怎么映射的呢?
2.两个实例解释 X 如何个映射法。
实例1:投一枚硬币,出现正面和反面的概率近似1/2.
实例2:明天下雨或者晴天的可能均为1/2.
现在我们定义为(实质上反应到数学表达上,即用X映射):

很明显,事件 “正 反 雨 晴”是样本点 ω ,这些事件反应到数轴上即为:“0 1” ,“ 1 0”.
而表格可知,这两个不同的场景都遵循一个规则:
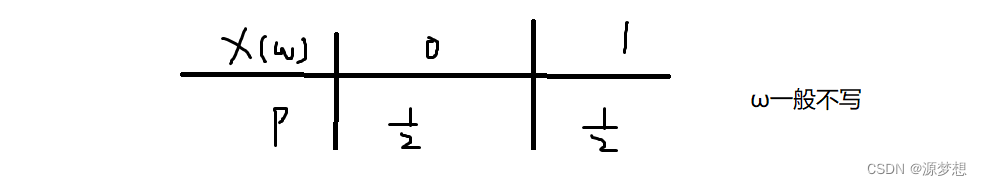
都抽象成了 X(ω) 这种规则,即 " X(ω) "将现实中的事件,变成了抽象的数字,方便进行数学处理,如:我们可以引入 微积分 这种强大的工具。
也可以说:随机变量 X 将一个随机不确定的过程,带入了又具体表示的数学世界,将“凌乱的概率” 变的有迹可循(如:我们可以用F(x) 表示X的概率分布)。
3.回过头看随机变量 X 的定义
设随机试验 E 的样本空间 Ω = { ω } ,如果对于每一个 事件ω ∈ Ω,都有唯一的实数 x ∈ R 与之对应。并且 对于 ∀x ∈ R ,有 {ω | X <= x, ω ∈ Ω}是随机事件,则称定义在 Ω 上的实值单值函数 X(ω) 为随机变量,记 X.
定义的意思是:随机变量是:“定义在样本空间 Ω 上,而取决于实数轴的函数”叫随机变量。
2.X 的分布函数 F(X) 的理解。
1.定义
设 X 是一个随机变量,称函数 F(x) = p { X<= x } (x ∈ R), 为随机变量 X 的分布函数,或称 X 服从F(X) 分布,记 X ~ F(x)。
2.解析定义
①X 的分布函数
分布,即概率。“X的分布函数",又可以说 “X的概率函数”。
通常有:幂函数,指数函数,三角函数。我们发现“幂 指数 三角”都反应了这种函数的规则 “f” (f也可以看作一个过程)。类比,”X的概率函数“是否反应了某种规则呢?
当然,“X的概率函数”也反应了一种规则。即 概率 。之所以我们很难理解 F(x) 是因为它的对应法则不符合我们通常的认知。
什么什么?概率也能是规则?当然可以对应法则(映射)是一个过程,那么 求 概率为何不能是一个过程呢?
重点:综上,那么 ”X的分布函数 F(x) = p{X<=x} " 即将 “{X<=x}” 这一坨东西,经过“P”求概率的过程,最终映射成了F(x), 故F(x)就是概率.
那么我们接下来的疑问就是, “{X <= x}”这一坨了,它是个啥?凭啥它就可以求概率了?
它还真可以求,因为"{X <= x}"表示的是一个或多个 “样本点” 或 “事件” 。事件当然可以求概率,为啥它就表示样本点了呢?
重点:由上对 X 的理解,X是将样本点映射到 数轴 上的一种法则,记X(ω) ,ω ∈ Ω
则 X 与 “x” (数轴上的点) 关系为 x = X(ω)。现在我们给出 x 的范围,即 " {X <= x} "是不是反解的结果就是样本点 ω 。
至此,我们已经完整知晓了 “x” 是怎样求出概率的,是通过 随机变量 X ,反解出 ω ,再通过 p 这个过程求出的 概率 F(x)。
而分布函数 F(x) 的对应法则 “F” 正是反应了这一过程,也因此,由于”X“ 规则的不同,导致 F(x) 规则的不同 常见有:

②F(x) = p { X<= x }
F(x) = p { X<= x },求的是概率,由 x 经过两次映射,一次是 逆映射 通过X法则 反解出 样本点ω ,再通过一次正映射 p{ } 求出事件概率,两次映射规则,共同构成从实数轴x 到 现实具体事件概率 的 "F"法则。
注:这里并不关心 P{ } 如何映射的 以及 X 的规则又是个啥,我们只关心 F(x) 到底是个啥,到底干了啥,咋来的,为什么要来就可以了。
③ (x ∈ R)
因为 x 是数轴上的取值,当然是R(由上可知)
3.为啥F(x) 不叫 x 的分布函数,叫 X 的分布函数
①可能分布二字对于 事件来说 更合适些,x还没有经过 X 转换成 ω 。
②可能这样说不够形象,明确。
3.F(X) 的充要条件
1.F(x)的充要条件 <=> ①②③
①F(x)是不减函数
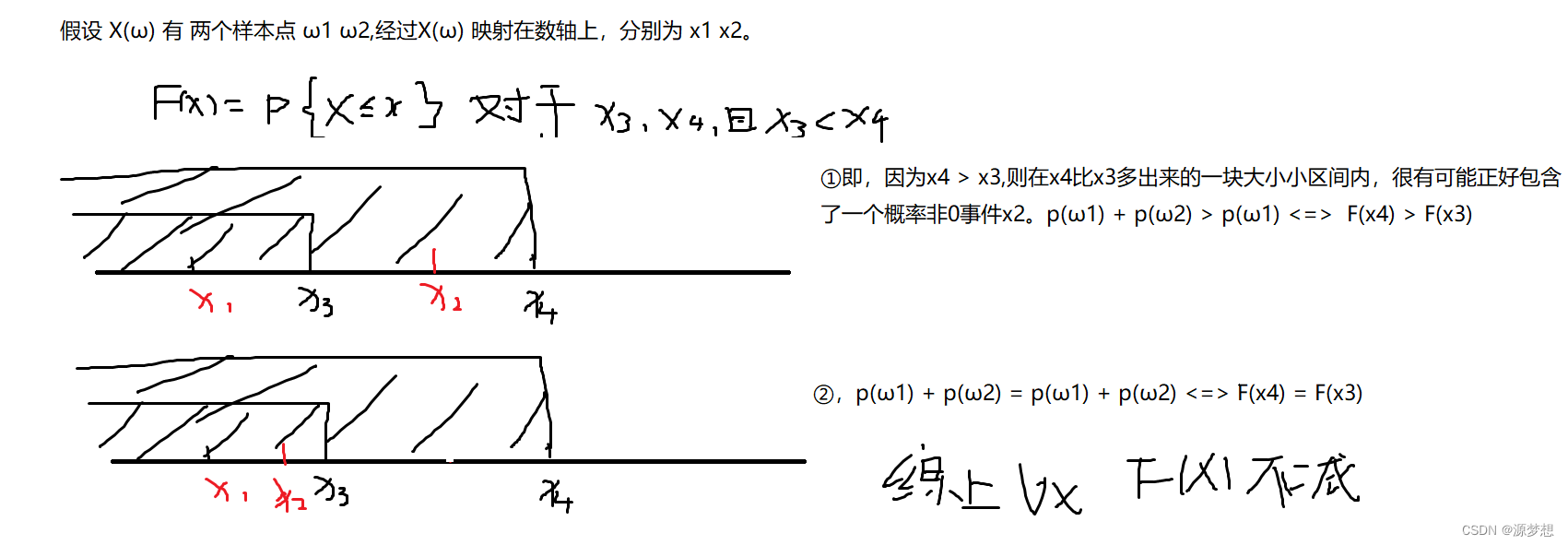
②F(x)是x0的右连续函数,x0 ∈ R。

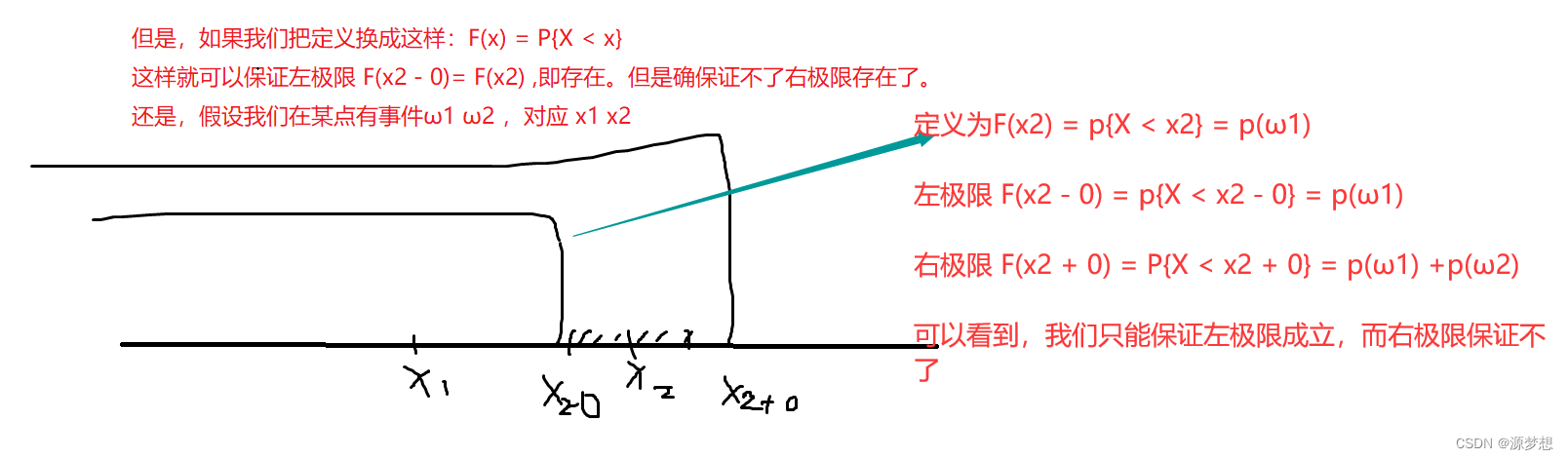
注:考研大纲明确规定,要求分布函数F(x)定义是F(x) = p{X <= x}
③F(-∞) = 0,F(+∞) = 1
F(-∞) = 0 , 一个事件不包含
F(+∞) = 1,包含全部事件。
4.经典例题
明天写
相关文章:

随机变量X,分布函数X~F(x)的理解。
1.随机变量X 1.通常认知的"x"与随机变量X 我们通常意义上的 x 是自变量,y f(x) 中的自变量。 但是 X 更多意义是 对应法则 " f " ,X完整写法是 X(ω) ω ∈ Ω。 X这个对应法则,可以将样本点映射到实数轴上。 那么X这…...

11.构造器的查询.分块.聚合
学习要点: 1.构造器查询 2.分块.聚合 本节课我们来开始学习数据库的构造器查询以及分块和聚合查询。 一.构造器查询 1. table()方法引入相应的表,get()方法可以查询当前表的所有数据; //获取全部结果 $users DB::table(users)-&g…...
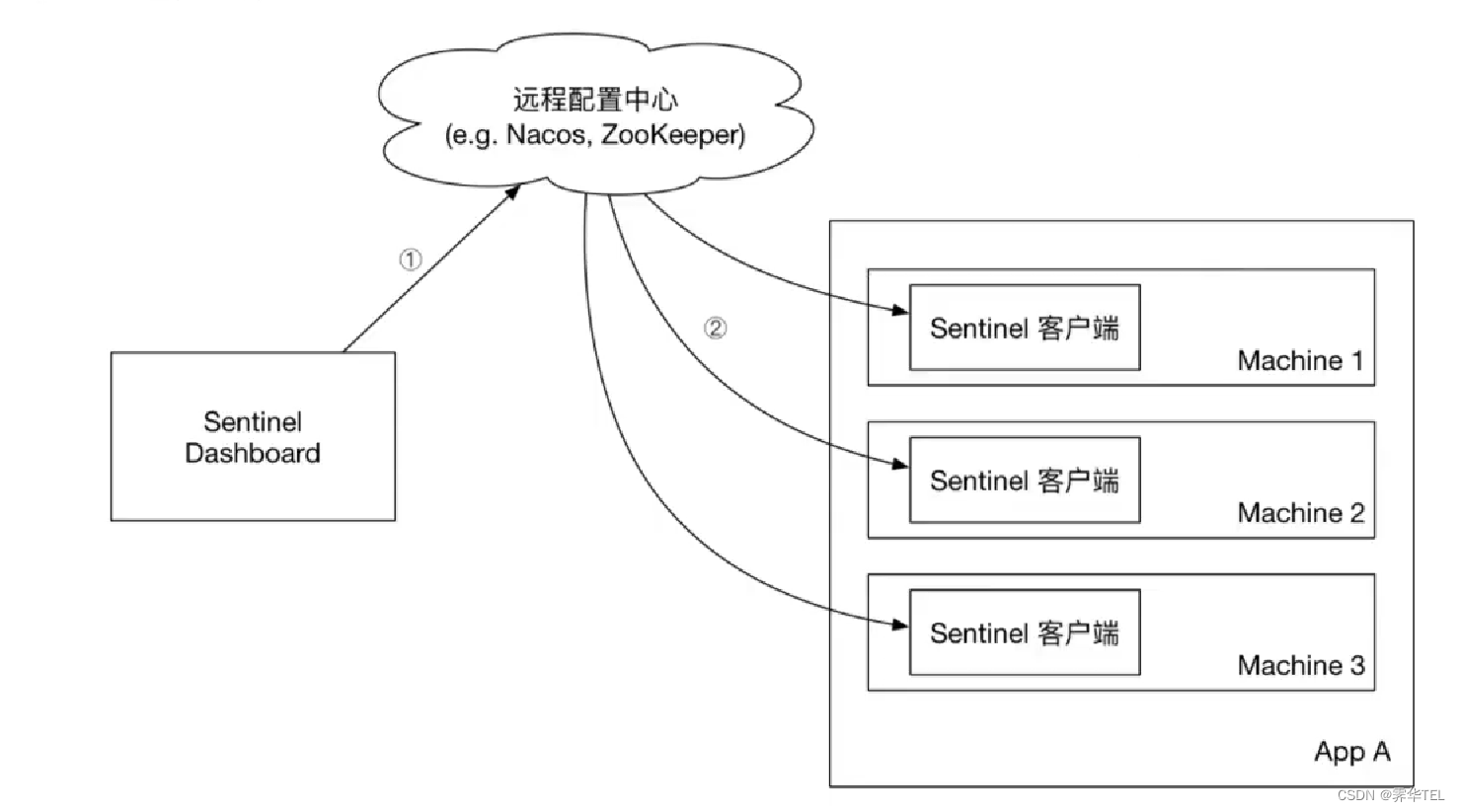
微服务保护——Sentinel
初识Sentinel 雪崩问题 微服务调用链路中的某个服务故障,引起整个链路中的所有微服务都不可用,这就是雪崩。 解决雪崩问题的常见方式有四种: 超时处理:设定超时时间,请求超过一定时间没有响应就返回错误信息,不会无休止等待舱壁…...

MySQL面试整理
https://houchen-study.oss-cn-hangzhou.aliyuncs.com/%E9%9D%A2%E8%AF%95/MySQL/MySQL%E9%9D%A2%E8%AF%95%E5%A4%A7%E5%85%A8%281%29.pdf 数据库基础知识 为什么要使用数据库? 什么是MySQL? 数据库的三大范式是什么? MySQL有关权限的表…...
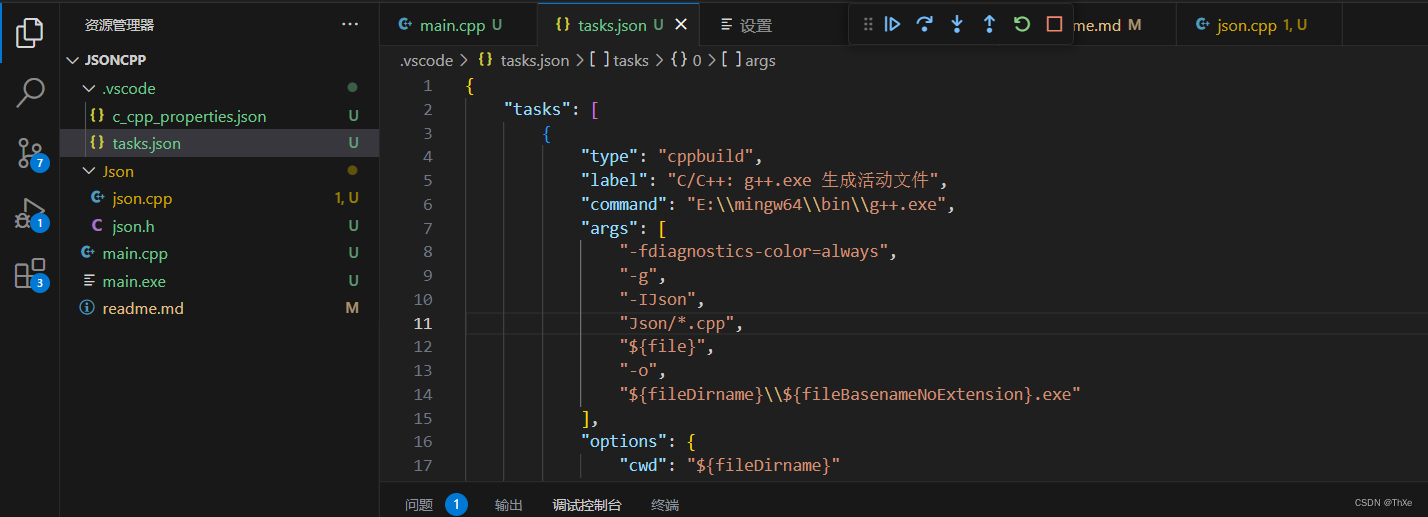
Vscode C++环境配置
多文件编译 打开设置搜索coderunner 找到Executor Map 加入-I目录名 目录名/*.cpp 调试 点击调试以后会产生tasks.json文件,加入链接文件和库文件...

matlab小波去噪
本文将为您介绍如何利用MATLAB进行小波去噪处理,并应用于实际数据。小波去噪是一种通过对数据进行小波分解和重构的方法,有效地去除信号中的噪声,提高信号质量。该方法不仅广泛应用于信号处理、图像处理等领域,在实际生产和科研中…...

为什么要采用全网营销策略?全网营销有何优势?
现在市场上有很多全网营销公司,其实很多企业的经理人疑惑全网营销是要干什么?这些公司能干什么?这里小马识途营销顾问给大家做一个整体的解读。 全网营销,概括地说就是在整个互联网,利用各类互联网平台和工具对产品和服…...
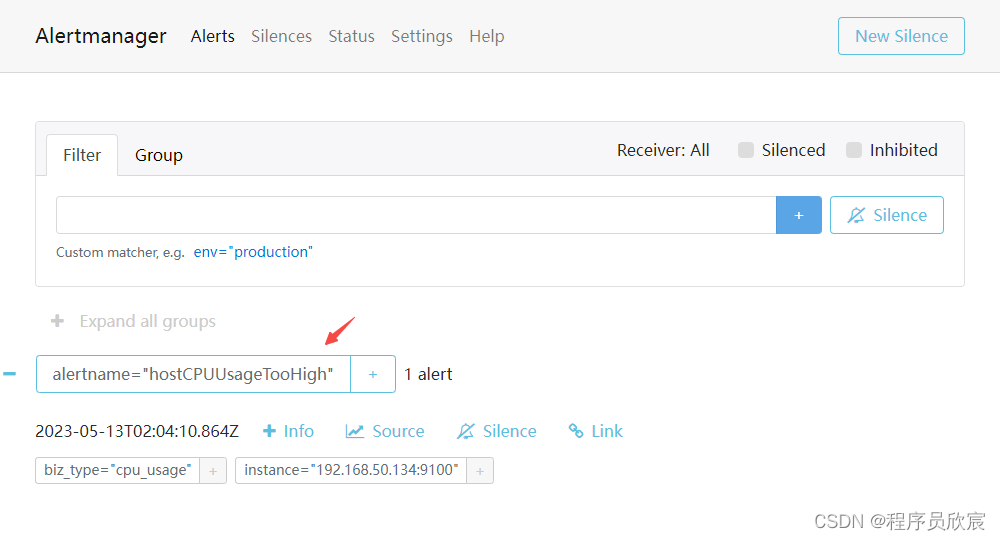
prometheus实战之四:alertmanager的部署和配置
欢迎访问我的GitHub 这里分类和汇总了欣宸的全部原创(含配套源码):https://github.com/zq2599/blog_demos 本篇概览 本文是《prometheus实战》系列的第四篇,在《prometheus实战之三:告警规则》中曾经提到过,整个告警功能分为规则和…...

【Python】glob 包的介绍和使用
glob 是 Python 标准库中的一个模块,它提供了一种查找符合特定模式的路径名的方法,类似于命令行中的 glob 命令。glob 模块用于读取指定路径下的所有符合特定规律的文件名,非常适合用于读取文件夹中的文件列表和操作符合特定规律文件列表。 …...

剑指offer(C++)-JZ48:最长不含重复字符的子字符串(算法-动态规划)
作者:翟天保Steven 版权声明:著作权归作者所有,商业转载请联系作者获得授权,非商业转载请注明出处 题目描述: 请从字符串中找出一个最长的不包含重复字符的子字符串,计算该最长子字符串的长度。 数据范围…...

两阶段最小二乘法
两阶段最小二乘法 文章目录 两阶段最小二乘法[toc]1、ivreg包介绍2 、R语言实现 1、ivreg包介绍 R语言计量包ivreg用以解决线性回归模型的内生性问题。 描述:工具变量估计的线性模型通过两阶段最小二乘(2SLS) 回归或通过稳健回归M估计(2SM)或MM估计(2SMM)。主要的…...
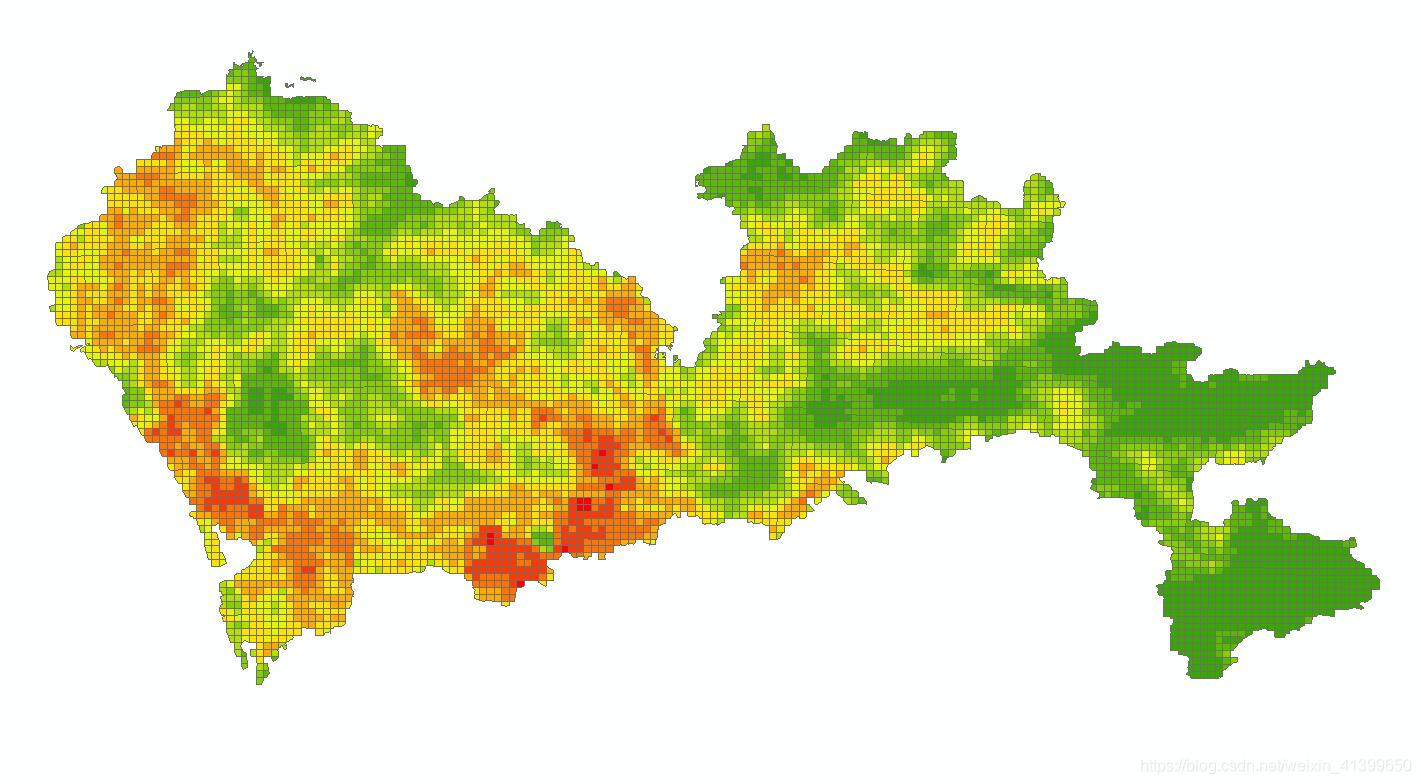
ArcMap创建格网统计图
目录 前言 一、人口数据获取 来源一:中科院地理所公开数据集 来源二:WorldPop数据集 二、人口格网统计步骤 1.创建渔网 2.人口数据处理 2.1 栅格转点 2.2 空间插值——处理人口缺失数据 2.3 空间连接——渔网人口统计 总结 前言 在科研中&am…...
[VAE] Auto-Encoding Variational Bayes
直接看paper看得云里雾里,李沐视频一语道破天机(建议从30min左右开始看GAN到Diffusion的串讲)。VAE的核心思路就是下面: 做生成,其实就是从随机向量(z)到目标图像(x)的过…...

《程序员面试金典(第6版)》面试题 16.19. 水域大小(深度优先搜索,类似棋盘类问题,八皇后的简化版本,C++)
题目描述 你有一个用于表示一片土地的整数矩阵land,该矩阵中每个点的值代表对应地点的海拔高度。若值为0则表示水域。由垂直、水平或对角连接的水域为池塘。池塘的大小是指相连接的水域的个数。编写一个方法来计算矩阵中所有池塘的大小,返回值需要从小到…...
Spring 注解之@RestController与@Controller的区别
目录 1:介绍 2:区别 3:总体来说 4:社区地址 1:介绍 RestController 和 Controller 是 Spring MVC 中常用的两个注解,它们都可以用于定义一个控制器类。 2:区别 返回值类型不同:…...

Java中的泛型是什么?如何使用泛型
Java中的泛型是指在定义类、接口和方法时使用类型参数,以使得这些类、接口和方法可以操作多种类型的数据,从而提高代码的重用性和安全性。Java的泛型机制是从JDK5开始引入的,它使得Java程序员能够编写更加通用和类型安全的代码。 什么是泛型…...

【飞行棋】多人游戏-微信小程序开发流程详解
可曾记得小时候玩过的飞行棋游戏,是90后的都有玩过吧,现在重温一下,这是一个可以二到四个人参与的游戏,通过投骰子走棋,一开始靠运气,后面还靠自己选择,谁抢占先机才能赢,还可以和小…...

力扣 146. LRU 缓存
一、题目描述 请你设计并实现一个满足LRU(最近最少使用)缓存约束的数据结构。 实现 LRUCache 类: LRUCache(int capacity) 以正整数作为容量 capacity 初始化LRU缓存。int get(int key) 如果关键字 key 存在于缓存中,则返回关键…...

关于Oracle SCN的最大阈值
SCN每秒增长的速度跟Oracle的版本有关,在Oracle 11.2.0.2之前是每秒允许最大增长16384,在Oracle 11.2.0.2之后是默认每秒允许增长32768,这个值跟新增的隐含参数_max_reasonable_scn_rate有关,如下所示: NAME …...

Linux多路转接之poll
文章目录 一、poll的认识二、编写poll方案服务器三、poll方案多路转接的总结 一、poll的认识 多路转接技术是在不断更新进步的,一开始多路转接采用的是select方案,但是select方案存在的缺点比较多,所以在此基础上改进,产生了poll…...

[特殊字符] 智能合约中的数据是如何在区块链中保持一致的?
🧠 智能合约中的数据是如何在区块链中保持一致的? 为什么所有区块链节点都能得出相同结果?合约调用这么复杂,状态真能保持一致吗?本篇带你从底层视角理解“状态一致性”的真相。 一、智能合约的数据存储在哪里…...
)
【位运算】消失的两个数字(hard)
消失的两个数字(hard) 题⽬描述:解法(位运算):Java 算法代码:更简便代码 题⽬链接:⾯试题 17.19. 消失的两个数字 题⽬描述: 给定⼀个数组,包含从 1 到 N 所有…...

第一篇:Agent2Agent (A2A) 协议——协作式人工智能的黎明
AI 领域的快速发展正在催生一个新时代,智能代理(agents)不再是孤立的个体,而是能够像一个数字团队一样协作。然而,当前 AI 生态系统的碎片化阻碍了这一愿景的实现,导致了“AI 巴别塔问题”——不同代理之间…...

vue3 定时器-定义全局方法 vue+ts
1.创建ts文件 路径:src/utils/timer.ts 完整代码: import { onUnmounted } from vuetype TimerCallback (...args: any[]) > voidexport function useGlobalTimer() {const timers: Map<number, NodeJS.Timeout> new Map()// 创建定时器con…...

Java数值运算常见陷阱与规避方法
整数除法中的舍入问题 问题现象 当开发者预期进行浮点除法却误用整数除法时,会出现小数部分被截断的情况。典型错误模式如下: void process(int value) {double half = value / 2; // 整数除法导致截断// 使用half变量 }此时...

人工智能--安全大模型训练计划:基于Fine-tuning + LLM Agent
安全大模型训练计划:基于Fine-tuning LLM Agent 1. 构建高质量安全数据集 目标:为安全大模型创建高质量、去偏、符合伦理的训练数据集,涵盖安全相关任务(如有害内容检测、隐私保护、道德推理等)。 1.1 数据收集 描…...

五子棋测试用例
一.项目背景 1.1 项目简介 传统棋类文化的推广 五子棋是一种古老的棋类游戏,有着深厚的文化底蕴。通过将五子棋制作成网页游戏,可以让更多的人了解和接触到这一传统棋类文化。无论是国内还是国外的玩家,都可以通过网页五子棋感受到东方棋类…...

针对药品仓库的效期管理问题,如何利用WMS系统“破局”
案例: 某医药分销企业,主要经营各类药品的批发与零售。由于药品的特殊性,效期管理至关重要,但该企业一直面临效期问题的困扰。在未使用WMS系统之前,其药品入库、存储、出库等环节的效期管理主要依赖人工记录与检查。库…...

2025年- H71-Lc179--39.组合总和(回溯,组合)--Java版
1.题目描述 2.思路 当前的元素可以重复使用。 (1)确定回溯算法函数的参数和返回值(一般是void类型) (2)因为是用递归实现的,所以我们要确定终止条件 (3)单层搜索逻辑 二…...

DAY 45 超大力王爱学Python
来自超大力王的友情提示:在用tensordoard的时候一定一定要用绝对位置,例如:tensorboard --logdir"D:\代码\archive (1)\runs\cifar10_mlp_experiment_2" 不然读取不了数据 知识点回顾: tensorboard的发展历史和原理tens…...
