只要学会这些AI工具，一个人就是一家营销咨询公司
本教程收集于：AIGC从入门到精通教程
只要学会这些AI工具，一个人就是一家营销咨询公司
随着AI工具的不断涌现，您只需掌握市面上热门的AI工具，便可独自开展营销咨询公司。通过一系列AI工具，您可以为企业提供全案服务，收获丰厚回报。
例如，在协助一家美妆初创公司出海时，我们运用一系列A
相关文章：
只要学会这些AI工具，一个人就是一家营销咨询公司
本教程收集于：AIGC从入门到精通教程 只要学会这些AI工具，一个人就是一家营销咨询公司 随着AI工具的不断涌现，您只需掌握市面上热门的AI工具，便可独自开展营销咨询公司。通过一系列AI工具，您可以为企业提供全案服务，收获丰厚回报。 例如，在协助一家美妆初创公司出海时，…...
[离散数学] 函数
文章目录 函数判断函数的条件复合函数复合函数的性质 逆函数 函数 判断函数的条件 dom F A ⇔ \Leftrightarrow ⇔所有x 都有 F（x）与之对应 有唯一的与其对应 < x , y > ∈ f ∧ < y , z > ∈ f ⇒ y z <x,y>\in f \land <y,z…...
好家伙，又一份牛逼笔记面世了...
最近网传的一些裁员的消息，搞的人心惶惶。已经拿到大厂offer的码友来问我：大厂还能去，去了会不会被裁。 还在学习的网友来问我：现在还要冲互联网么？ 我是认为大家不用恐慌吧，该看啥看啥，该学啥…...
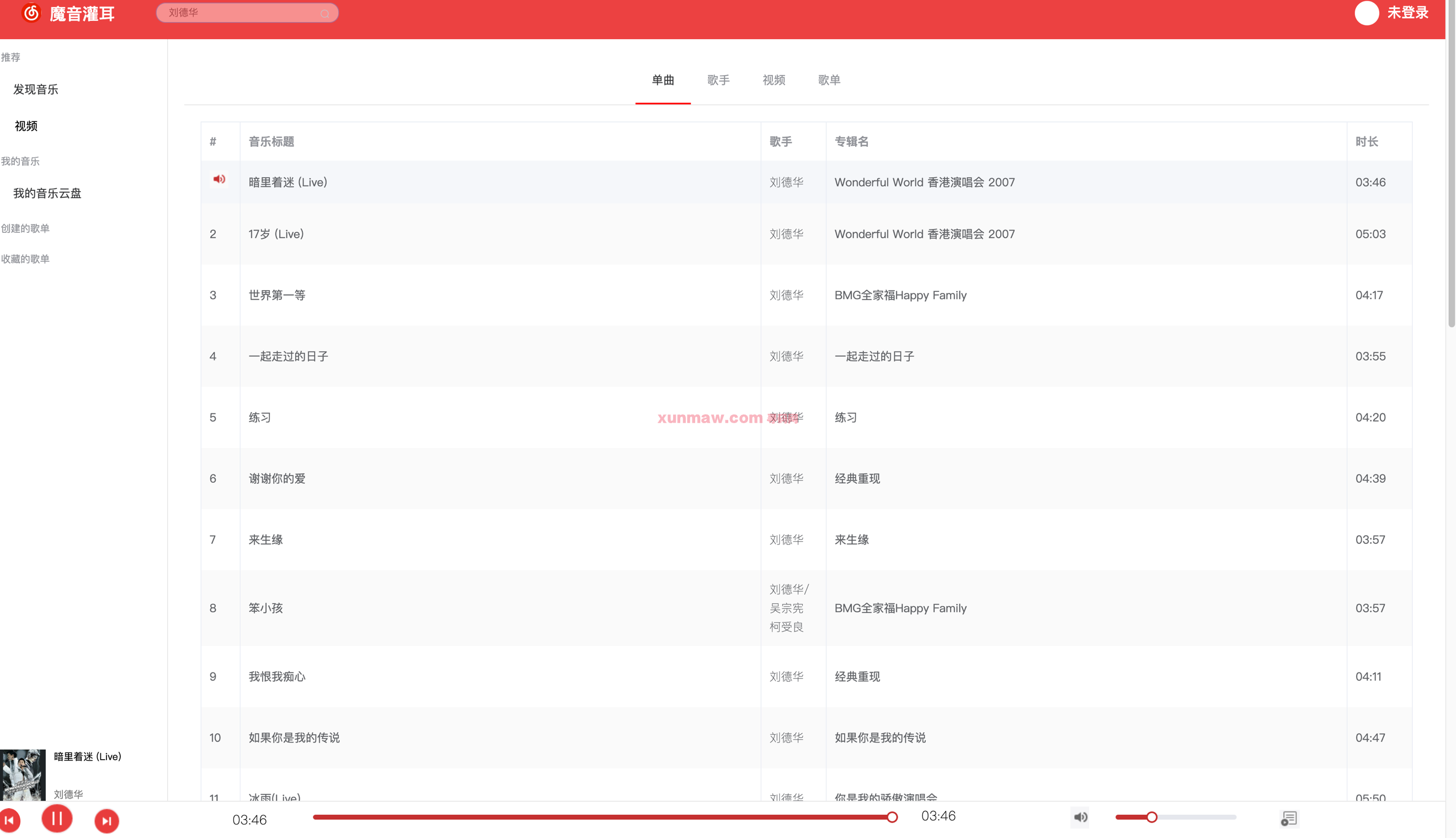
基于nodejs+vue3 的高仿网易云音乐
大家好，我是小寻，欢迎大家关注我的公众号：工具优选，加入前端、java群聊哦！ 今天给大家分享一个超高水准的项目：基于nodejsvue3研发的高仿网易云音乐，项目内容出自寻码网！ 技术栈&a…...
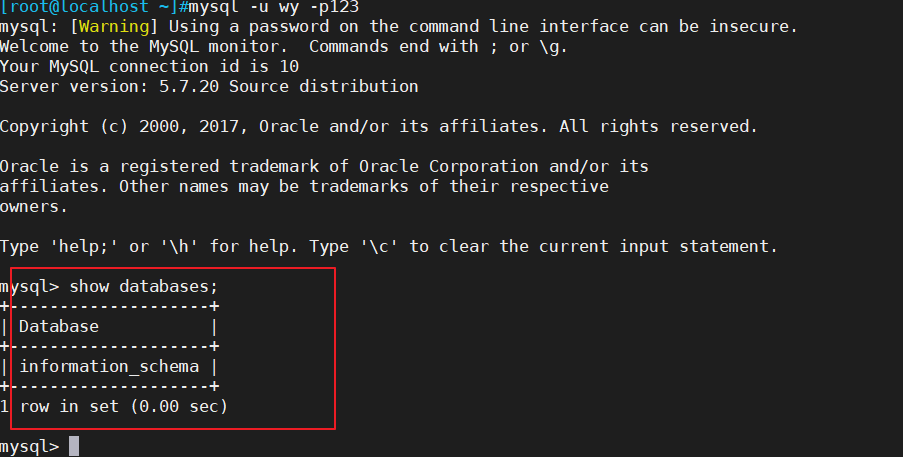
MySQL数据库用户管理以及数据库用户授权
一、数据库用户管理 1、新建用户 CREATE USER 用户名来源地址 [IDENTIFIED BY [PASSWORD] 密码]; ---------------------------------------------------------------------------------------------------------- 用户名：指定将创建的用户名 来源地址：…...
全面分析生物技术的优缺点以及应用场景
一、 引言 生物识别技术具有不可撤销性、高度便利性和较低错误率等优势，在安全领域中也备受瞩目。然而，对于生物识别技术在应对安全挑战方面的可靠性和有效性，但争议并未被完全解决 二、生物识别技术的介绍 所谓生物识别技术就是，…...
OpenAI是什么？
OpenAI是一家人工智能技术公司，成立于2015年，总部位于美国旧金山。它的创始人包括埃隆马斯克等多名知名人士，公司的目标是推进人工智能技术的发展，同时确保人工智能的发展不会对人类造成负面影响。 OpenAI在研究和开发各种人工智能…...
量子计算——新兴领域的前沿技术
随着人类社会文明的不断进步，计算技术也在不断发展。传统计算机在过去的几十年中快速发展，计算速度、存储能力等方面发生了天翻地覆的变化。但随着大数据、人工智能、区块链等新兴领域的迅速崛起，传统计算机的发展似乎面临了瓶颈。在这样的背…...
.Net平台下OpenGL绘制图形（1）(VS2019,Winform,C#)
1、介绍 OpenGL（英语：Open Graphics Library，译名：开放图形库或者“开放式图形库”）是用于渲染2D、3D矢量图形的跨语言、跨平台的应用程序编程接口（API）。这个接口由近350个不同的函数调用组成…...
Casso的创作纪念日
机缘 注册CSDN的时候才刚上大学，到现在使用CSDN已经四年了，距发布第一篇文章却只刚过去一百多天，刚看到这个提醒消息的时候只感慨时间过得真快，自己也在慢慢成长着，当初刚开始学习的时候，查资料用得最多的就…...
Bernhard‘s Talk on Towards Causal NLP 笔记
因果学习系列笔记 这是我的 GitHub 因果学习笔记仓库 https://github.com/xin007-kong/ryCausalLearning，欢迎 star🤩 讲者是 Bernhard Schlkopf talk 链接：(41) Bernhard Schoelkopf | Towards Causal NLP | KeynoteEMNLP 2021 Causal Infer…...
ES6模块化规范
在没有ES6模块化规范前，有像AMD、CMD这样的浏览器模块化规范，还有像CommonJS这样的服务端模块化规范。 2015年，JS终于推出了官方的模块化规范，为了统一各种规范，我们简称ES6 模块化。 ES6目前作为JS的内置模块化系统&a…...
红黑树下岗，内核新数据结构上场：maple tree！
在外界看来，Linux 内核的内部似乎变化很少，尤其是像内存管理子系统（memory-management subsystem）这样的子系统。然而，开发人员时常需要更换内部接口来解决某些长期存在的问题。比如，其中一个问题就是用来保…...
Angular开发之——Angular打包部署项目(04)
一 概述 ng build 构建应用lite-server介绍及安装lite-server部署应用IIS管理器部署应用 二 ng build 构建应用 2.1 执行如下指令构建应用 ng build2.2 构建完成后，会创建一个 dist 文件夹 2.3 直接打开index.html会出错(需要借助于服务器部署) 三 lite-server介…...
深度优先搜索算法思想，题型总结与题目清单（不断更新）
深度优先搜索 深度优先搜索（Depth-First Search，简称DFS）是一种用于遍历或搜索树或图的算法。这个名称直接来自于这个算法的操作方式：它沿着某一路径深入遍历直到无法继续，然后再回溯进行下一条路径的遍历。 DFS的主要…...
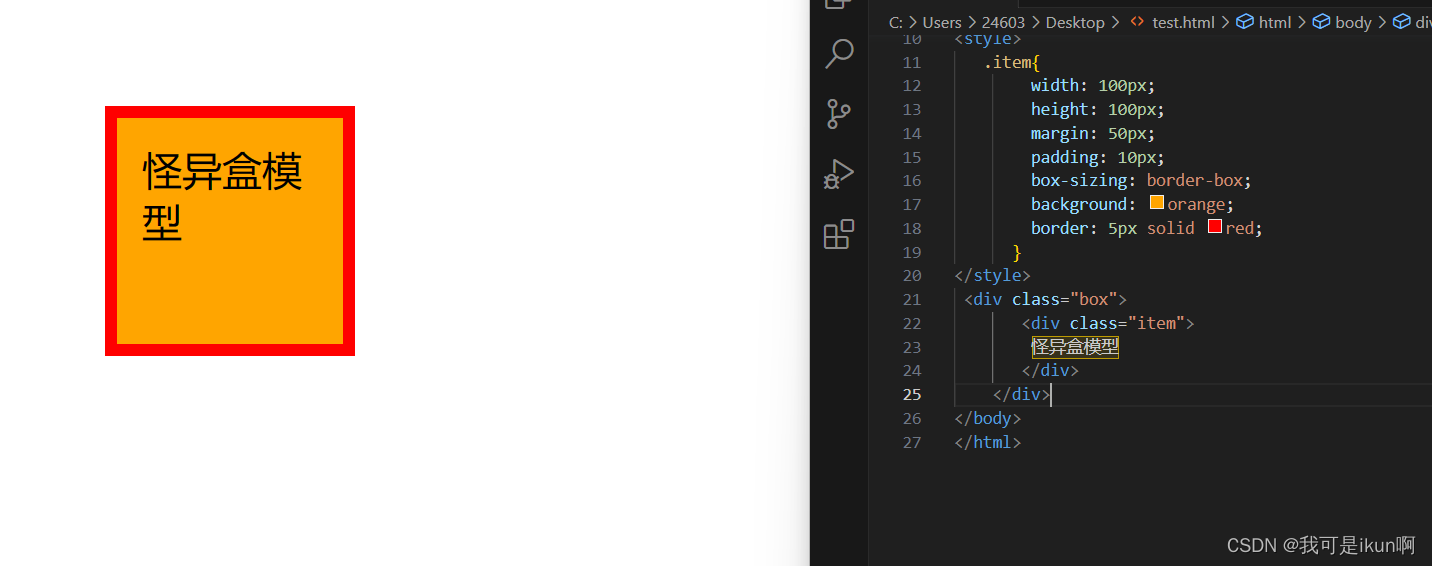
网页三剑客之 CSS
css 在这里不会介绍太多，我们主要重点介绍两个：选择器和盒子模型就够用了。这里看个乐就好了，没有那么多重点，只是简单的认识一下下CSS。 CSS 是什么 CSS 是层叠样式表 (Cascading Style Sheets)的缩写它存在的意义就是…...
Maven（1）--- Maven入门指南
当然，我可以为你提供Maven的详细介绍，并按照6篇文章的方式进行详细展开。下面是第一篇的内容，采用Markdown格式输出： Maven入门指南 什么是Maven？ Maven是一个强大的项目管理工具，被广泛应用于Java项目开…...
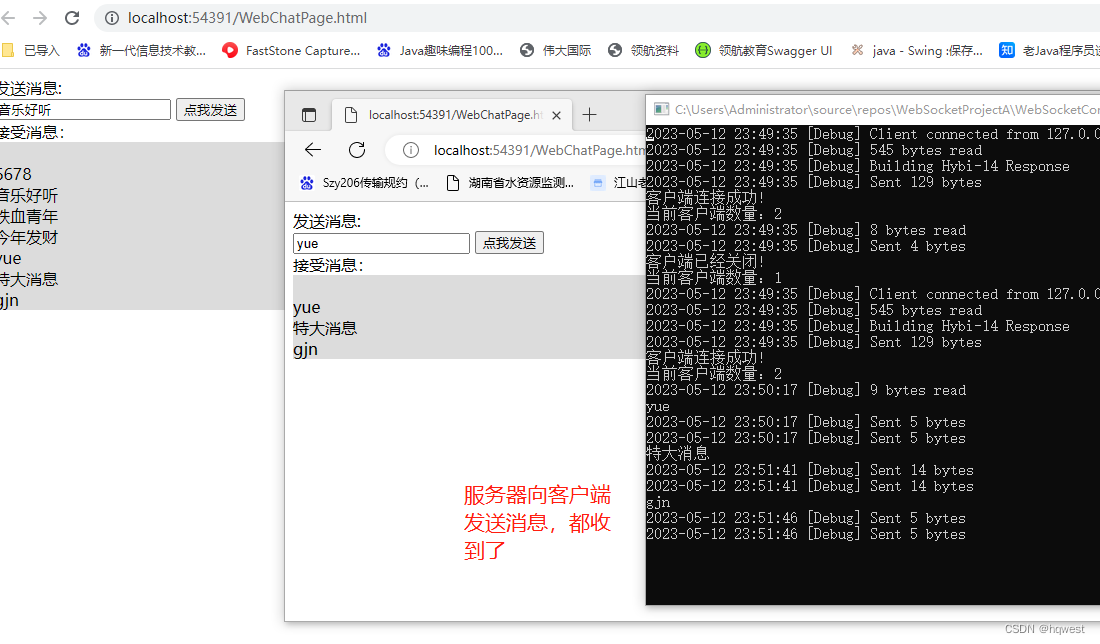
C# 实现 Websocket通讯聊天 (管用、超好使，点个赞)
1、背景 WebSocket出现之前，Web端为了实现即时通讯，所用的技术都是Ajax轮询(polling)。轮询是在特定的的时间间隔（如每1秒），由浏览器对服务器发出HTTP request，然后由服务器返回最新的数据给客服端的浏览器…...
知识点回顾（一）
1.final,finally ,finalize final?修饰符（关键字）如果一个类被声明为final，意味着它不能再派生出新的子类，不能作为父类被继承。因此一个类不能既被声明为 abstract的，又被声明为final的。将变量或方法声明为final&…...
verflow属性的常用值详解
什么是overflow 在CSS中，overflow是“溢出”的意思，该属性规定当内容溢出元素框时发生的事情，设置内容是否会被修剪，溢出部分是否会被隐藏；例如当属性值设置为“visible”则内容不会被修剪，为“hidden”则内…...
Zustand 状态管理库：极简而强大的解决方案
Zustand 是一个轻量级、快速和可扩展的状态管理库，特别适合 React 应用。它以简洁的 API 和高效的性能解决了 Redux 等状态管理方案中的繁琐问题。 核心优势对比 基本使用指南 1. 创建 Store // store.js import create from zustandconst useStore create((set)…...
【力扣数据库知识手册笔记】索引
索引 索引的优缺点 优点1. 通过创建唯一性索引，可以保证数据库表中每一行数据的唯一性。2. 可以加快数据的检索速度（创建索引的主要原因）。3. 可以加速表和表之间的连接，实现数据的参考完整性。4. 可以在查询过程中，…...
python/java环境配置
环境变量放一起 python： 1.首先下载Python Python下载地址：Download Python | Python.org downloads ---windows -- 64 2.安装Python 下面两个，然后自定义，全选 可以把前4个选上 3.环境配置 1）搜高级系统设置 2…...
渲染学进阶内容——模型
最近在写模组的时候发现渲染器里面离不开模型的定义，在渲染的第二篇文章中简单的讲解了一下关于模型部分的内容，其实不管是方块还是方块实体，都离不开模型的内容 🧱 一、CubeListBuilder 功能解析 CubeListBuilder 是 Minecraft Java 版模型系统的核心构建器，用于动态创…...
蓝桥杯3498 01串的熵
问题描述 对于一个长度为 23333333的 01 串, 如果其信息熵为 11625907.5798， 且 0 出现次数比 1 少, 那么这个 01 串中 0 出现了多少次? #include<iostream> #include<cmath> using namespace std;int n 23333333;int main() {//枚举 0 出现的次数//因…...
docker 部署发现spring.profiles.active 问题
报错： org.springframework.boot.context.config.InvalidConfigDataPropertyException: Property spring.profiles.active imported from location class path resource [application-test.yml] is invalid in a profile specific resource [origin: class path re…...
人工智能--安全大模型训练计划：基于Fine-tuning + LLM Agent
安全大模型训练计划：基于Fine-tuning LLM Agent 1. 构建高质量安全数据集 目标：为安全大模型创建高质量、去偏、符合伦理的训练数据集，涵盖安全相关任务（如有害内容检测、隐私保护、道德推理等）。 1.1 数据收集 描…...
Spring AOP代理对象生成原理
代理对象生成的关键类是【AnnotationAwareAspectJAutoProxyCreator】，这个类继承了【BeanPostProcessor】是一个后置处理器 在bean对象生命周期中初始化时执行【org.springframework.beans.factory.config.BeanPostProcessor#postProcessAfterInitialization】方法时…...
项目进度管理软件是什么？项目进度管理软件有哪些核心功能？
无论是建筑施工、软件开发，还是市场营销活动，项目往往涉及多个团队、大量资源和严格的时间表。如果没有一个系统化的工具来跟踪和管理这些元素，项目很容易陷入混乱，导致进度延误、成本超支，甚至失败。 项目进度管理软…...
MySQL EXPLAIN 命令详解
文章目录 MySQL EXPLAIN 命令详解EXPLAIN 输出的基本结构id2. select_type3. table4. partitions5. type6. possible_keys7. key8. key_len9. ref10. rows11. filtered12. Extra 使用 EXPLAIN 的注意事项示例 MySQL EXPLAIN 命令详解 EXPLAIN 是 MySQL 中一个非常有用的命令&a…...