15- 决策回归树, 随机森林, 极限森林 (决策树优化) (算法)
- 1. 决策回归树:
from sklearn.tree import DecisionTreeRegressor
model = DecisionTreeRegressor(criterion='mse',max_depth=3)
model.fit(X,y) # X是40个点 y是一个圆- 2. 随机森林 + 稳定预测:
from sklearn.ensemble import RandomForestClassifier
# model = RandomForestClassifier()
# model.fit(X_train,y_train)
score = 0
for i in range(100):model = RandomForestClassifier()model.fit(X_train,y_train)score += model.score(X_test,y_test)/100
print('随机森林平均准确率是:',score) - 3. 极限森林:
from sklearn.ensemble import ExtraTreesClassifier
clf3 = ExtraTreesClassifier(max_depth = 3)
clf3.fit(X_train,y_train)1、决策回归树原理概述
-
与分类树一样
-
裂分指标,使用的是MSE、MAE
-
决策回归树,认为它是分类问题,只是,分的类别多一些!!!
-
只要树,分类回归,其实就是分类多和少的问题
2、决策回归树算例
2.1、决策树预测圆的轨迹
2.1.1 导包并创建数据与可视化
import numpy as np
from sklearn.tree import DecisionTreeRegressor
from sklearn import tree
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
import matplotlib.pyplot as plt
import graphviz
X = np.linspace(0,2*np.pi,40).reshape(-1,1)
X_test = np.linspace(0,2*np.pi,187).reshape(-1,1)
# y 一个正弦波,余弦波,圆
y = np.c_[np.sin(X),np.cos(X)]
plt.figure(figsize=(3,3))
plt.scatter(y[:,0],y[:,1])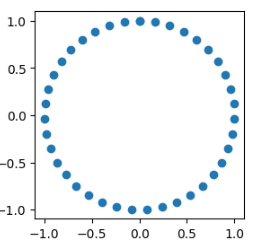
2.1.2 使用线性回归预测,看效果
linear = LinearRegression()
linear.fit(X,y) #将数据交给算法,学习,希望算法,找到规律
# X ----> y 是一个圆;预测X_test返回值y_ 如果预测好,也是圆
y_ = linear.predict(X_test)
plt.figure(figsize=(3,3))
plt.scatter(y_[:,0],y_[:,1])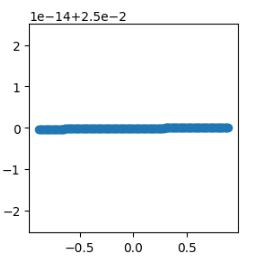
2.1.3 使用决策树回归,看效果
model = DecisionTreeRegressor(criterion='mse',max_depth=3)
model.fit(X,y)#X 是40个点 y是一个圆
y_ = model.predict(X_test) #X_test是187点,预测y_应该是一个圆
# 请问y_中有多少数据???
print(y_.shape)
plt.figure(figsize=(6,6))
plt.scatter(y_[:,0],y_[:,1],color = 'green')
plt.savefig('./3-决策树回归效果.png',dpi = 200)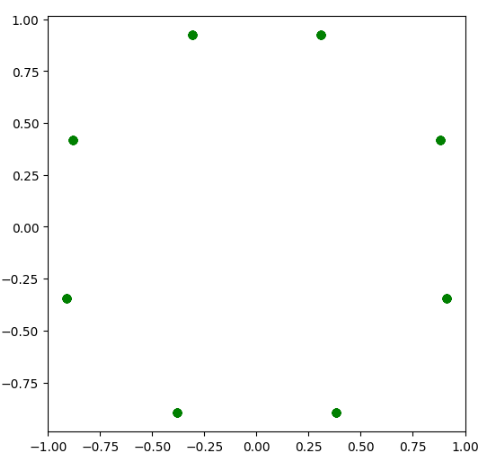
2.1.4 决策回归树可视化
# 决策树形状
dot_data = tree.export_graphviz(model,filled=True)
graph = graphviz.Source(dot_data)
graph.render('./1-决策回归树')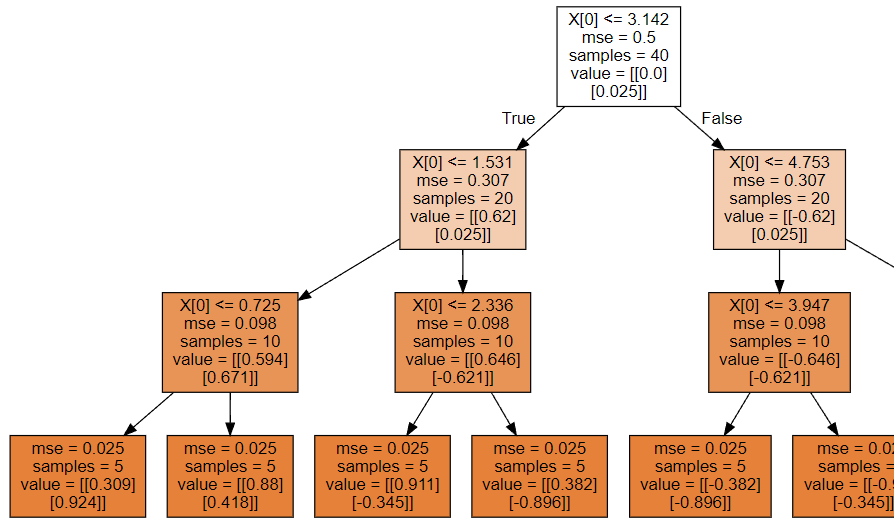
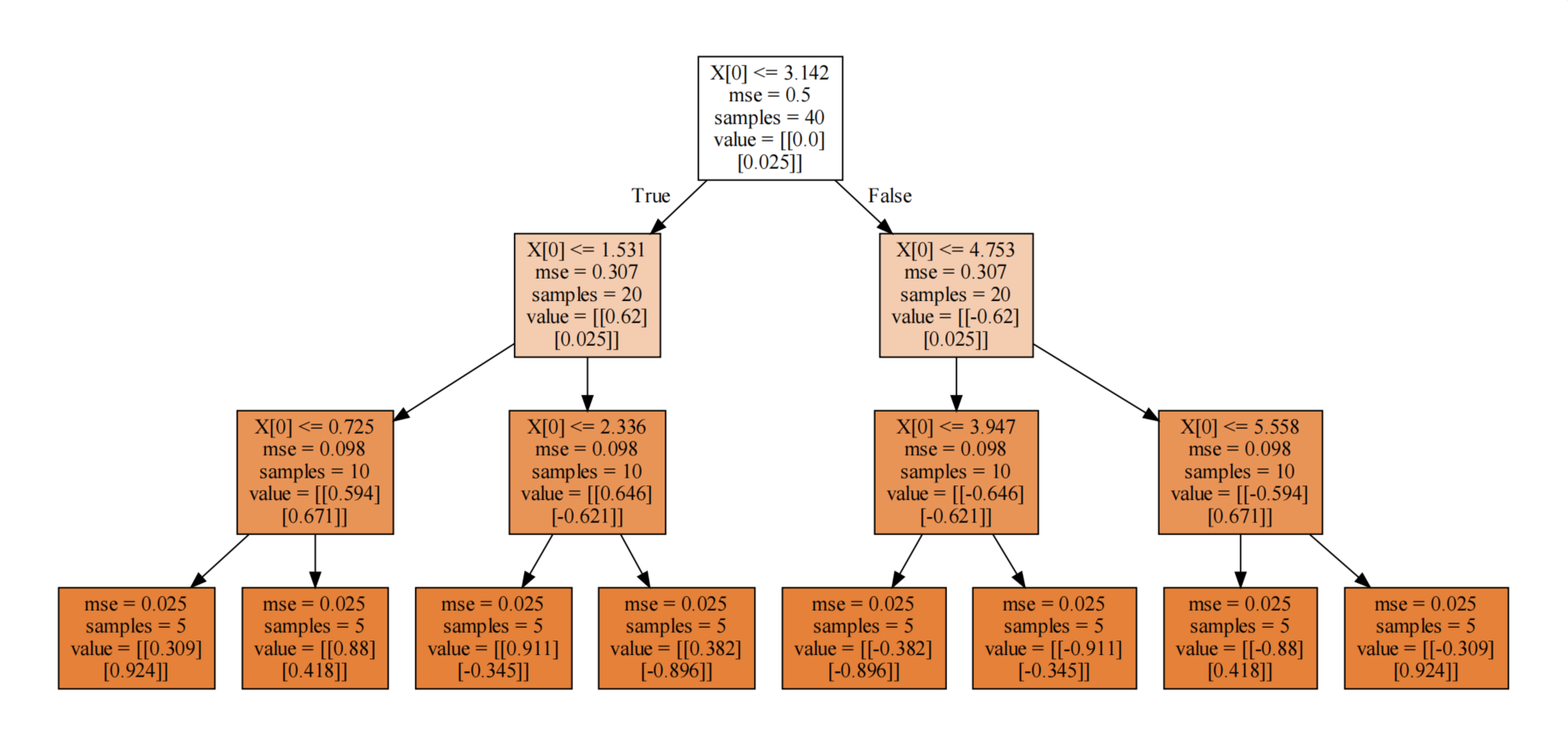
因为决策树深度是3,所以最终得到8个叶节点,所以分成8类!
2.2、增加决策树深度
model = DecisionTreeRegressor(criterion='mse',max_depth=4)
model.fit(X,y)#X 是40个点 y是一个圆
y_ = model.predict(X_test) #X_test是187点,预测y_应该是一个圆
# 请问y_中有多少数据???
print(y_.shape)
plt.figure(figsize=(6,6))
plt.scatter(y_[:,0],y_[:,1],color = 'green')
plt.savefig('./4-增加深度决策树回归效果.png',dpi = 200)
# 决策树形状
dot_data = tree.export_graphviz(model,filled=True)
graph = graphviz.Source(dot_data)
graph.render('./5-增加深度决策回归树')
2.3、决策回归树分裂原理剖析
以上面深度为3的决策树为例
1、计算未分裂时,整体MSE:
mse = ((y - y.mean(axis = 0))**2).mean()
print('未分裂时,整体MSE:',mse)2、根据分裂标准X[0] <= 3.142,计算分裂后的MSE:
cond = X <= 3.142
part1 = y[cond.reshape(-1)]
part2 = y[(~cond).reshape(-1)]
mse1 = ((part1 - part1.mean(axis = 0))**2).mean()
mse2 = ((part2 - part2.mean(axis = 0))**2).mean()
print(mse1,mse2)3、寻找最佳分裂条件:
split_result = {}
mse_lower = 0.5
for i in range(len(X) - 1):split = round(X[i:i + 2].mean(),3)cond = X <= splitpart1 = y[cond.reshape(-1)]part2 = y[(~cond).reshape(-1)]mse1 = ((part1 - part1.mean(axis = 0))**2).mean()mse2 = ((part2 - part2.mean(axis = 0))**2).mean()mse = mse1 * len(part1)/cond.size + mse2 * len(part2)/cond.sizemse_result.append(mse)if mse < mse_lower:split_result.clear()split_result[split] = [i,mse]mse_lower = mse
print('最佳分裂条件:',split_result)根据打印输出,我们知道最佳裂分,索引是:19。分裂条件是:3.142。
结论:和直接使用决策回归树绘图显示的结果一模一样~
3、决策回归树 VS 线性回归
1、加载数据 (糖尿病数据)
import numpy as np
from sklearn.tree import DecisionTreeRegressor
from sklearn import tree
from sklearn import datasets
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
diabetes = datasets.load_diabetes()#糖尿病
X = diabetes['data']
y = diabetes['target']
X_train,X_test,y_train,y_test = train_test_split(X,y,random_state = 911)2、线性回归表现
linear = LinearRegression()
linear.fit(X_train,y_train)
linear.score(X_test,y_test) # 0.413943154014099873、决策树回归表现
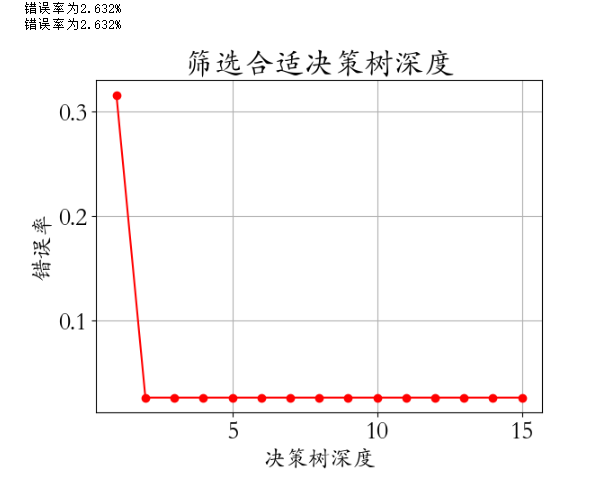
import matplotlib.pyplot as plt
plt.rcParams['font.family'] = 'STKaiti'
max_depth = np.arange(1,16)
score = []
for d in max_depth:model = DecisionTreeRegressor(max_depth = d)model.fit(X_train,y_train)score.append(model.score(X_test,y_test))
plt.plot(max_depth,score,'ro-')
plt.xlabel('max_depth',fontsize = 18)
plt.ylabel('Score',fontsize = 18)
plt.title('决策树准确率随着深度变化',pad = 20,fontsize = 20)
plt.savefig('./6-决策树回归糖尿病.png',dpi = 200)
4、结论
-
对于这个案例,线性回归效果更好一些
-
糖尿病这个数据,更适合使用方程对规律进行拟合
-
在很多方面,决策树回归表现也优秀~
4、集成算法
4.1、集成算法概述
集成算法核心:
- 少数服从多数,人多力量大,三个臭皮匠顶个诸葛亮。
聚合模型:
- 所有朋友的意见投票, 少数服从多数(随机森林对应原理公式)
- 牛一点的朋友多给几票,弱鸡一点的少给几票(Adaboost对应原理公式)
4.2、构造不同模型(朋友)
- 同样的数据,行列都相同,不同的超参数,可以得到不同的模型。
- 同样的超参数,行相同,列不同,可以得到不同的模型。
- 同样的超参数,行不同,列相同,可以得到不同的模型。
- 同样的超参数,同样的数据,但是数据权重不同,可以得到不同的模型。
4.3、集成算法不同方式
-
方式一Bagging(套袋法)
-
对训练集进行抽样, 将抽样的结果用于训练 g(x)。
-
并行,独立训练。
-
随机森林random forest便是这一类别的代表。
-
-
方式二Boosting(提升法)
-
利用训练集训练出模型,根据本次模型的预测结果,调整训练集。
-
然后利用调整后的训练集训练下一个模型。
-
串行,需要第一个模型。
-
Adaboost,GBDT,Xgboost都是提升树算法典型代表。
-
4.4、Bagging集成算法步骤
-
Bootstrap(独立自主) : 有放回地对原始数据集进行均匀抽样
-
利用每次抽样生成的数据集训练模型
-
最终的模型为每次生成的模型进行投票
-
其实 boosting 和 bagging 都不仅局限于对决策树这种基模型适应
-
如果不是同一种 base model,也可以做集成算法
5、随机森林
5.1、随机森林介绍
Bagging 思想 + 决策树就诞生了随机森林。
随机森林,都有哪些随机?
-
bagging生成一颗决策树时,随机抽样
-
抽样后,分裂时,每一个结点都随机选择特征,从部分特征中筛选最优分裂条件
5.2、随机森林实战
1、导包加载数据
import numpy as np
from sklearn import tree
from sklearn import datasets
from sklearn.model_selection import train_test_split
import graphviz
# ensemble 集成
# 随机森林
from sklearn.ensemble import RandomForestClassifier
# 作为对照
from sklearn.linear_model import LogisticRegression
from sklearn.tree import DecisionTreeClassifier
# 加载数据
X,y = datasets.load_iris(return_X_y=True)
X_train,X_test,y_train,y_test = train_test_split(X,y,random_state = 112)2、普通决策树
score = 0
for i in range(100):X_train,X_test,y_train,y_test = train_test_split(X,y)model = DecisionTreeClassifier()model.fit(X_train,y_train)score += model.score(X_test,y_test)/100
print('随机森林平均准确率是:',score) # 0.94868421052631493、随机森林(运行时间稍长,10s)
score = 0
for i in range(100):X_train,X_test,y_train,y_test = train_test_split(X,y)model = RandomForestClassifier()model.fit(X_train,y_train)score += model.score(X_test,y_test)/100
print('随机森林平均准确率是:',score) # 随机森林平均准确率是: 0.9457894736842095结论:
-
和决策树对比发现,随机森林分数稍高,结果稳定
-
即降低了结果方差,减少错误率
4、逻辑斯蒂回归
import warnings
warnings.filterwarnings('ignore')
score = 0
for i in range(100):X_train,X_test,y_train,y_test = train_test_split(X,y)lr = LogisticRegression()lr.fit(X_train,y_train)score += lr.score(X_test,y_test)/100
print('逻辑斯蒂回归平均准确率是:',score) # 0.9602631578947363结论:
-
逻辑斯蒂回归这个算法更加适合鸢尾花这个数据的分类
-
随机森林也非常优秀
5.3、随机森林可视化
1、创建随机森林进行预测
X_train,X_test,y_train,y_test = train_test_split(X,y,random_state = 9)
forest = RandomForestClassifier(n_estimators=100,criterion='gini')
forest.fit(X_train,y_train)
score1 = round(forest.score(X_test,y_test),4)
print('随机森林准确率:',score1) # 1.0
print(forest.predict_proba(X_test))2、对比决策树
X_train,X_test,y_train,y_test = train_test_split(X,y,random_state = 112)
model = DecisionTreeClassifier()
model.fit(X_train,y_train)
print('决策树准确率:',model.score(X_test,y_test))
proba_ = model.predict_proba(X_test)
print(proba_)总结:
-
一般情况下,随机森林比决策树更加优秀
-
随机森林,是多棵树投票的概率,所以predict_proba()概率值,出现0.97
-
单一决策树,不是,通过投票,而是通过决策树叶节点分类,所以概率要么是0,要么是1
3、绘制决策树
dot_data = tree.export_graphviz(forest[0],filled=True)
graph = graphviz.Source(dot_data)
graph
# 第五十颗树类别
dot_data = tree.export_graphviz(forest[49],filled=True)
graph = graphviz.Source(dot_data)
graph
# 第100颗树类别
dot_data = tree.export_graphviz(forest[-1],filled=True)
graph = graphviz.Source(dot_data)
graph5.4、随机森林总结
随机森林主要步骤:
-
随机选择样本(放回抽样);
-
随机选择特征;
-
构建决策树;
-
随机森林投票(平均)
优点:
-
表现良好
-
可以处理高维度数据(维度随机选择)
-
辅助进行特征选择
-
得益于 Bagging 可以进行并行训练
缺点:
-
对于噪声过大的数据容易过拟合
6、极限森林
6.1、极限森林介绍
极限森林,都有哪些随机?
-
极限森林中每一个决策树都采用原始训练集
-
抽样后,分裂时,每一个结点分裂时,都进行特征随机抽样(一部分特征作为分裂属性)
-
从分裂随机中筛选最优分裂条件
6.2、极限森林实战
1、加载数据
import warnings
warnings.filterwarnings('ignore')
import numpy as np
from sklearn.ensemble import RandomForestClassifier,ExtraTreesClassifier
from sklearn.tree import DecisionTreeClassifier
from sklearn import datasets
from sklearn.model_selection import train_test_split
import graphviz
from sklearn import tree# 加载数据
X,y = datasets.load_wine(return_X_y=True)
X_train,X_test,y_train,y_test = train_test_split(X,y,random_state = 119)2、单棵决策树
clf = DecisionTreeClassifier()
clf.fit(X_train,y_train)
print('单棵决策树得分:',clf.score(X_test,y_test)) # 0.9555555555555556
print('数据特征:',clf.n_features_) # 13
print('节点分裂选择最大特征数量:',clf.max_features_) # 133、随机森林
clf2 = RandomForestClassifier()
clf2.fit(X_train,y_train)
print('随机森林得分:',clf2.score(X_test,y_test)) # 1.0
print('数据特征:',clf2.n_features_) # 13
for t in clf2:print('节点分裂选择最大特征数量:',t.max_features_) # 34、极限森林
clf3 = ExtraTreesClassifier(max_depth = 3)
clf3.fit(X_train,y_train)
print('极限森林得分:',clf3.score(X_test,y_test))
print('数据特征:',clf3.n_features_)
for t in clf3:print('节点分裂选择最大特征数量:',t.max_features_)5、可视化
dot_data = tree.export_graphviz(clf3[0],filled=True)
graph = graphviz.Source(dot_data)
dot_data = tree.export_graphviz(clf3[49],filled=True)
graph = graphviz.Source(dot_data)6、分裂标准代码演练
6.1、计算未分裂gini系数
count = []
for i in range(3):count.append((y_train == i).sum())
count = np.array(count)
p = count / count.sum()
gini = (p * (1 - p)).sum()
print('未分裂,gini系数是:',round(gini,3)) # 未分裂,gini系数是: 0.6536.2、根据属性寻找最佳分裂条件
f = np.sort(X_train[:,11])
gini_lower = 1
best_split = {}
for i in range(len(f) - 1):split = round(f[i:i + 2].mean(),3)cond = X_train[:,11] <= splitpart1 = y_train[cond]part2 = y_train[~cond]# 计算每一部分的gini系数count1 = []count2 = []for j in range(3):count1.append((part1 == j).sum())count2.append((part2 == j).sum())count1,count2 = np.array(count1),np.array(count2)p1 = count1 / count1.sum()p2 = count2 / count2.sum()gini1 = round((p1 * (1 - p1)).sum(),3)gini2 = round((p2 * (1 - p2)).sum(),3)# 计算整体的gini系数gini = round(gini1 * count1.sum()/(y_train.size) + gini2 * count2.sum()/(y_train.size),3)if gini < gini_lower:gini_lower = ginibest_split.clear()best_split[j] = splitprint(split,gini1,gini2,gini,count1,count2)
print(best_split,gini_lower)结论:
-
通过打印输出可知,极限森林分裂条件,并不是最优的
-
并没有使用gini系数最小的分裂点
-
分裂值,具有随机性,这正是极限森林的随机所在!
相关文章:

15- 决策回归树, 随机森林, 极限森林 (决策树优化) (算法)
1. 决策回归树: from sklearn.tree import DecisionTreeRegressor model DecisionTreeRegressor(criterionmse,max_depth3) model.fit(X,y) # X是40个点 y是一个圆 2. 随机森林 稳定预测: from sklearn.ensemble import RandomForestClassifier # model RandomForestC…...

Flink相关的记录
Flink源码编译首次编译的时候,去除不必要的操作,同时install会把Flink中的module安装到本地仓库,这样依赖当前module的其他组件就无需去远程仓库拉取当前module,节省了时间。mvn clean install -T 4 -DskipTests -Dfast -Dmaven.c…...
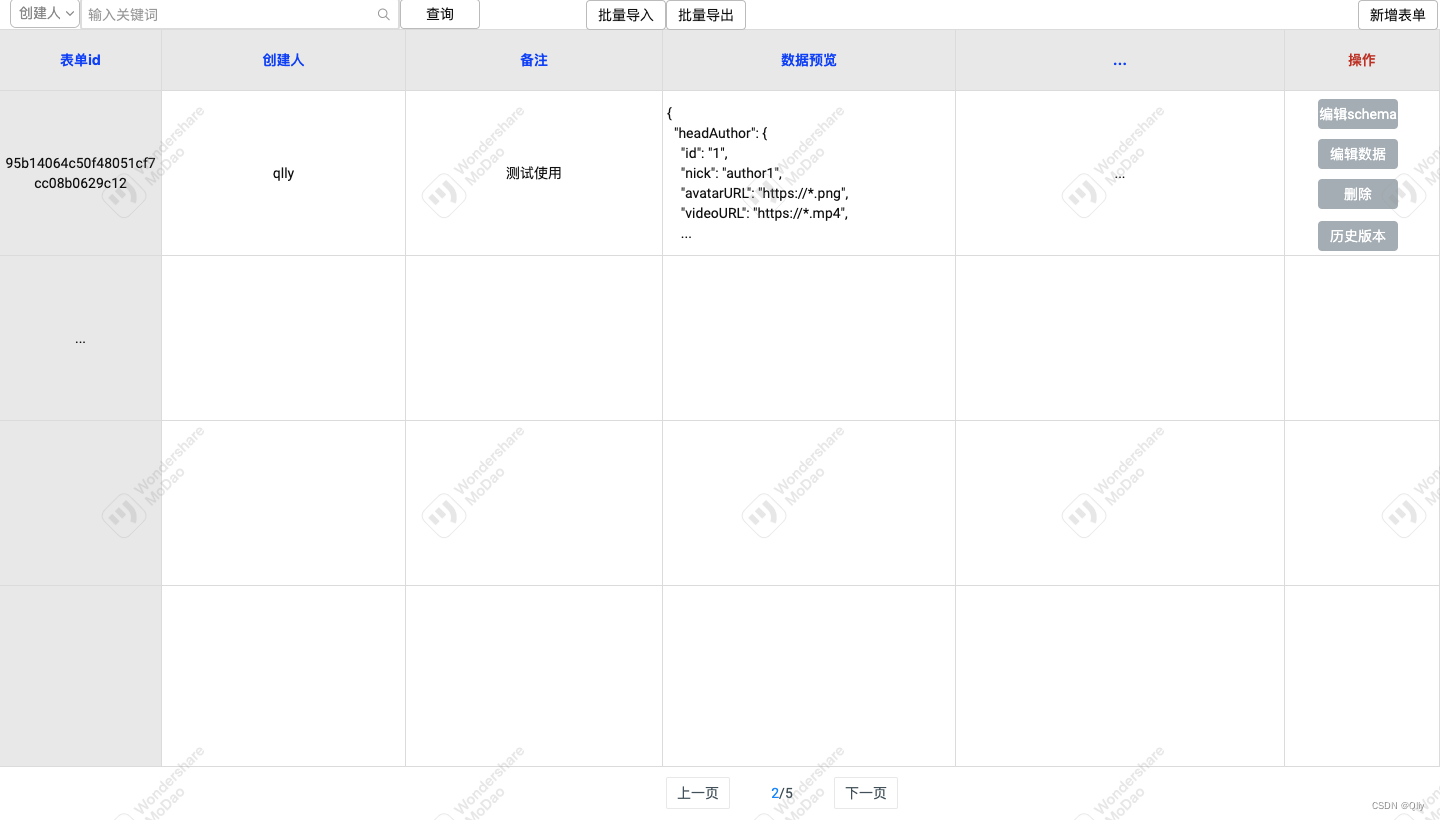
配置可视化-基于form-render的无代码配置服务(一)
背景 有些业务场景需要产品或运营去配置JSON数据提供给开发去使用(后面有实际业务场景的说明),原有的业务流程,非开发人员(后面直接以产品指代)把数据交给开发,再由开发去更新JSON数据。对于产…...
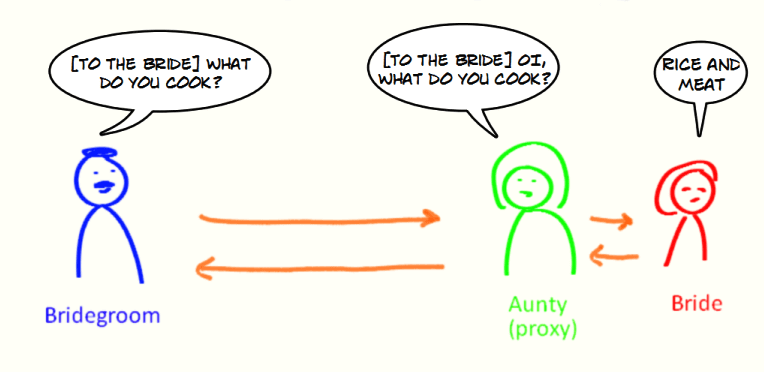
Java 代理模式详解
1、代理模式 代理模式是一种比较好理解的设计模式。简单来说就是 我们使用代理对象来代替对真实对象(real object)的访问,这样就可以在不修改原目标对象的前提下,提供额外的功能操作,扩展目标对象的功能。 代理模式的主要作用是扩展目标对象…...
知识付费小程序怎么做_分享知识付费小程序的作用
在线知识付费产业的主要业务逻辑是基于用户的主动学习需求,为其提供以跨领域基础知识与技能为核心的在线知识服务,提升其达到求知目的的效率。公众号和小程序的迅速发展,又为知识付费提供了技术支持,从而促进了行业的进一步发展。…...
14- 决策树算法 (有监督学习) (算法)
决策树是属于有监督机器学习的一种决策树算法实操: from sklearn.tree import DecisionTreeClassifier # 决策树算法 model DecisionTreeClassifier(criterionentropy,max_depthd) model.fit(X_train,y_train)1、决策树概述 决策树是属于有监督机器学习的一种,起源…...

如何编译和运行C++程序?
C 和C语言类似,也要经过编译和链接后才能运行。在《C语言编译器》专题中我们讲到了 VS、Dev C、VC 6.0、Code::Blocks、C-Free、GCC、Xcode 等常见 IDE 或编译器,它们除了可以运行C语言程序,还可以运行 C 程序,步骤是一样的&#…...

Golang 给视频添加背景音乐 | Golang工具
目录 前言 环境依赖 代码 总结 前言 本文提供给视频添加背景音乐,一如既往的实用主义。 主要也是学习一下golang使用ffmpeg工具的方式。 环境依赖 ffmpeg环境安装,可以参考我的另一篇文章:windows ffmpeg安装部署_阿良的博客-CSDN博客 …...

让AI护理医疗:解决卫生系统的痛点
一、引言 1.对医疗领域中AI技术的介绍 随着人工智能的不断发展,它已经成为了各个领域中的重要组成部分。在医疗领域中,AI技术也逐渐发挥着越来越重要的作用。从诊断到治疗,从健康管理到研究,人工智能已经深刻地影响着医疗领域的…...
Windows 离线安装 MySQL 8
目录 1. 下载离线安装包 2. 上传解压 3 配置 my.ini 文件 4 设置系统环境变量 5 安装 MySQL 6 登录 MySQL 客户环境是内网环境,不能访问外网,只能离线安装 MySQL 了。 1. 下载离线安装包 MySQL 离线压缩包官网下载地址:MySQL :: Down…...

【前端攻城狮之vue基础】02路由+嵌套路由+路由query/params传参+路由props配置+replace属性+编程式路由导航+缓存路由组件
路由的基础知识1.路由简介2.路由基本使用3.嵌套路由4.传递路由的query传参# 5.传递路由的params参数6.路由的props传参配置7.路由router-link标签的replace属性8.编程式路由导航9.缓存路由组件1.路由简介 路由是一条条对应的key-value关系,key就是前端地址栏的路径…...
CHAPTER 1 Zabbix介绍及安装
Zabbix介绍及安装1.1 Zabbix监控1 为什么要监控1.1 网站可用性2 监控什么东西2.1 监控范畴3 怎么来监控3.1 远程管理服务器3.2 监控硬件3.3 查看cpu相关3.4 内存3.5 磁盘3.6 监控网络4 监控工具总览5 zabbix介绍5.1 zabbix的组成5.2 zabbix监控范畴1.2 安装zabbix1 环境检查2 安…...

认识V模型、W模型、H模型
软件测试与软件工程息息相关,软件测试是软件工程组成中不可或缺的一部分。 在软件工程、项目管理、质量管理得到规范化应用的企业,软件测试也会进行得比较顺利,软件测试发挥的价值也会更大。 要关注软件工程、质量管理以及配置管理与软件测试…...

excel ttest检测
1、excel函数含义 TTEST(array1,array2,tails,type) ▪ Array1: 第一组数据集 ▪ Array2: 第二组数据集 ▪ Tails: 用于定义所返回的分布的尾数: 1 代表单尾;2 代表双尾 ▪ Type: 用于定义 t-检验的类型: 1 代表成对检验;2 代表双样本等方差假设&am…...
PDFPrinting.Net操作进行细粒度控制
PDFPrinting.Net操作进行细粒度控制 PDFPrinting.Net能够容易且灵活地预测完美的打印结果以及用户文件的示例性显示。可以快速浏览.NET PDF打印中最关键的元素。如果用户需要获得更详细的概述,那么他可以查看快速入门手册,甚至是现有文档的详细概述参考。…...

SegPGD
在这项工作中,我们提出了一种有效和高效的分割攻击方法,称为SegPGD。此外,我们还提供了收敛性分析,表明在相同次数的攻击迭代下,所提出的SegPGD可以创建比PGD更有效的对抗示例。此外,我们建议应用我们的Seg…...
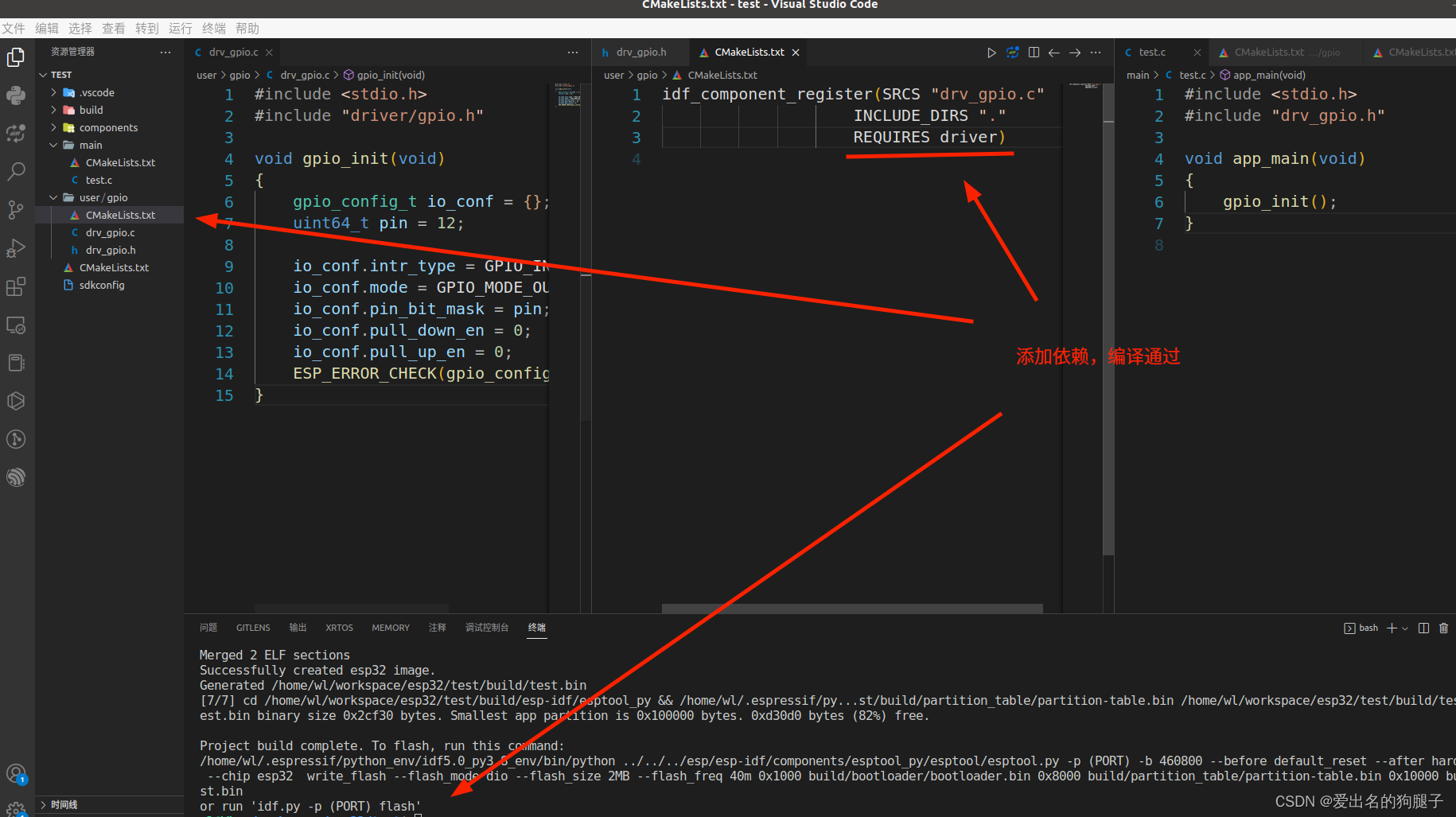
ESP-IDF + Vscode ESP32 开发环境搭建以及开发入门
ESP-IDF Vscode ESP32 开发环境搭建以及开发入门 文章目录ESP-IDF Vscode ESP32 开发环境搭建以及开发入门1. 前言2. 下载开发工具3. 配置工具4. 创建工程5. 解决vscode找不到头文件,波浪线警告6. 添加自己的组件6.1 组件说明6.2 添加项目组件6.3 添加扩展组件7. …...

SpringMvc的请求和响应
SpringMvc的数据响应 1.springmvc的数据相应方式 (1)页面跳转 直接返回字符串 通过ModelAndView对象返回 (2)回写数据 直接返回字符串 返回对象或集合 页面跳转 jsp页面 <% page contentType"text/html;charsetUTF-8&q…...

【Vue3】首页主体-面板组件封装
首页主体-面板组件封装 新鲜好物、人气推荐俩个模块的布局结构上非常类似,我们可以抽离出一个通用的面板组件来进行复用 目标:封装一个通用的面板组件 思路分析 图中标出的四个部分都是可能会发生变化的,需要我们定义为可配置主标题和副标题…...

部署 K8s 集群
1 .部署k8s的两种方式目前生产部署Kubernetes集群主要有两种方式:kubeadmKubeadm是一个K8s部署工具,提供kubeadm init和kubeadm join,用于快速部署Kubernetes集群。二进制包从github下载发行版的二进制包,手动部署每个组件&#x…...

生成xcframework
打包 XCFramework 的方法 XCFramework 是苹果推出的一种多平台二进制分发格式,可以包含多个架构和平台的代码。打包 XCFramework 通常用于分发库或框架。 使用 Xcode 命令行工具打包 通过 xcodebuild 命令可以打包 XCFramework。确保项目已经配置好需要支持的平台…...

django filter 统计数量 按属性去重
在Django中,如果你想要根据某个属性对查询集进行去重并统计数量,你可以使用values()方法配合annotate()方法来实现。这里有两种常见的方法来完成这个需求: 方法1:使用annotate()和Count 假设你有一个模型Item,并且你想…...

最新SpringBoot+SpringCloud+Nacos微服务框架分享
文章目录 前言一、服务规划二、架构核心1.cloud的pom2.gateway的异常handler3.gateway的filter4、admin的pom5、admin的登录核心 三、code-helper分享总结 前言 最近有个活蛮赶的,根据Excel列的需求预估的工时直接打骨折,不要问我为什么,主要…...

质量体系的重要
质量体系是为确保产品、服务或过程质量满足规定要求,由相互关联的要素构成的有机整体。其核心内容可归纳为以下五个方面: 🏛️ 一、组织架构与职责 质量体系明确组织内各部门、岗位的职责与权限,形成层级清晰的管理网络…...

屋顶变身“发电站” ,中天合创屋面分布式光伏发电项目顺利并网!
5月28日,中天合创屋面分布式光伏发电项目顺利并网发电,该项目位于内蒙古自治区鄂尔多斯市乌审旗,项目利用中天合创聚乙烯、聚丙烯仓库屋面作为场地建设光伏电站,总装机容量为9.96MWp。 项目投运后,每年可节约标煤3670…...

Aspose.PDF 限制绕过方案:Java 字节码技术实战分享(仅供学习)
Aspose.PDF 限制绕过方案:Java 字节码技术实战分享(仅供学习) 一、Aspose.PDF 简介二、说明(⚠️仅供学习与研究使用)三、技术流程总览四、准备工作1. 下载 Jar 包2. Maven 项目依赖配置 五、字节码修改实现代码&#…...

LLMs 系列实操科普(1)
写在前面: 本期内容我们继续 Andrej Karpathy 的《How I use LLMs》讲座内容,原视频时长 ~130 分钟,以实操演示主流的一些 LLMs 的使用,由于涉及到实操,实际上并不适合以文字整理,但还是决定尽量整理一份笔…...

提升移动端网页调试效率:WebDebugX 与常见工具组合实践
在日常移动端开发中,网页调试始终是一个高频但又极具挑战的环节。尤其在面对 iOS 与 Android 的混合技术栈、各种设备差异化行为时,开发者迫切需要一套高效、可靠且跨平台的调试方案。过去,我们或多或少使用过 Chrome DevTools、Remote Debug…...

STM32标准库-ADC数模转换器
文章目录 一、ADC1.1简介1. 2逐次逼近型ADC1.3ADC框图1.4ADC基本结构1.4.1 信号 “上车点”:输入模块(GPIO、温度、V_REFINT)1.4.2 信号 “调度站”:多路开关1.4.3 信号 “加工厂”:ADC 转换器(规则组 注入…...

Python的__call__ 方法
在 Python 中,__call__ 是一个特殊的魔术方法(magic method),它允许一个类的实例像函数一样被调用。当你在一个对象后面加上 () 并执行时(例如 obj()),Python 会自动调用该对象的 __call__ 方法…...
