时间轮算法概念
概述
在一些中间件中我们经常见到时间轮控制并发和熔断。
那么这个时间轮具体是什么呢,又是怎么使用的呢。
简介
其实时间轮可以简单的理解成我们日常生活中的时钟。
时钟里的指针一直在不停的转动,利用这个我们可以实现定时任务,目前linux里的crontab就是用的时间轮实现的。
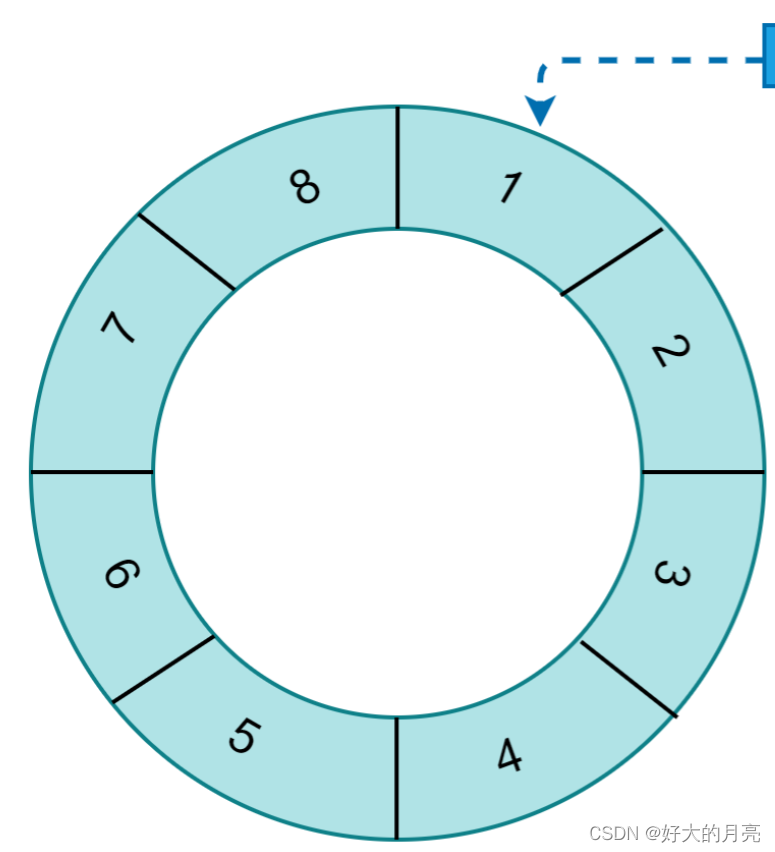
我们可以这么想象一下,时间轮就像一个环形链表,当秒针指向1刻度的时候其实就代表过去了1秒的时候,然后在1位置这个元素也是一个链表,从这个链表中取出多个任务去执行,这些被执行的任务就实现了延时1秒执行的需求。
再配个图来展示下
进一步深化理解
上面只是单个时间轮,但是实际中使用的场景会复杂很多,比如要延时一个月,这个时候上面这个单圈的时间轮的刻度就不够用了。
此时可以采用的方法:
1-扩展刻度
2-记录时间轮的圈数,当从指针指向的刻度中取任务时先对所有任务的round --,取出round=0的任务去执行
3-引入层级时间轮,再引入一个月时间轮,一个天时间轮,将任务拆分到上级时间轮中,当上级时间轮的指针取出任务时,如果时间还没到,就降级到下级时间轮,依次类推
上面3中方法中1肯定不采用,太离谱了,如果要扩展1万个刻度,太没效率了。
2和3都是可以采用的,不过3采用的多一点,拆分多个时间轮组合的形式更加灵活
相关文章:

时间轮算法概念
概述 在一些中间件中我们经常见到时间轮控制并发和熔断。 那么这个时间轮具体是什么呢,又是怎么使用的呢。 简介 其实时间轮可以简单的理解成我们日常生活中的时钟。 时钟里的指针一直在不停的转动,利用这个我们可以实现定时任务,目前lin…...
[SCTF2019]babyre 题解
对未来的真正慷慨,是把一切献给现在。 ——加缪 目录 1.查壳 2.处理花指令,找到main函数 这一操作过程可以参考下面的视频: 3.静态分析第一部分,psword1 4.静态分析第二部分,psword2 5.静态分析第五部分,psword3 6.根据ps…...

全志H3系统移植 | 移植主线最新uboot 2023.04和kernel 6.1.11到Nanopi NEO开发板
文章目录 环境说明uboot移植kernel移植rootfs移植测试环境说明 OS:Ubuntu 20.04.5 LTSGCC:arm-none-linux-gnueabihf-gcc 10.3.0编译器下载地址:Downloads | GNU-A Downloads – Arm Developer uboot移植 当前最新版本v2023.04-rc2下载地址:https://github.com/u-boot/u-…...

vue项目第四天
使用elementui tabplane组件实现历史访问记录组件的二次封装<el-tabs type"border-card"><el-tab-pane label"用户管理">用户管理</el-tab-pane><el-tab-pane label"配置管理">配置管理</el-tab-pane><el-tab-…...
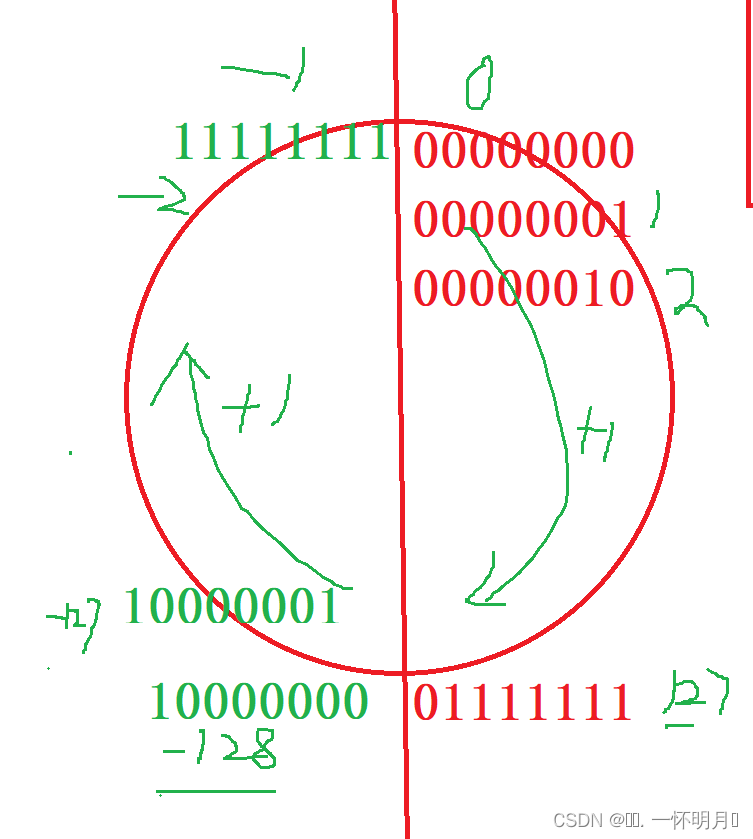
「C语言进阶」数据内存的存储
🚀🚀🚀大家觉不错的话,就恳求大家点点关注,点点小爱心,指点指点🚀🚀🚀 目录 🐰数据类型的介绍 🐰类型的意义 🐰数据类型的基本归类…...

面试必问:进程和线程的区别(从操作系统层次理解)
1.什么是进程?为什么要有进程? 进程有一个相当精简的解释:进程是对操作系统上正在运行程序的一个抽象。 这个概念确实挺抽象,仔细想想却也挺精准。 我们平常使用计算机,都会在同一时间做许多事,比如边看…...

ModuleNotFoundError: No module named ‘apex‘与 error: legacy-install-failure
ModuleNotFoundError: No module named ‘apex’ ModuleNotFoundError: No module named apex 表示 Python 在搜索模块时无法找到名为 apex 的模块。这通常是因为您没有安装 apex 模块或安装不正确。 apex 是一个针对混合精度训练和优化的 PyTorch 扩展库,您可以通过…...
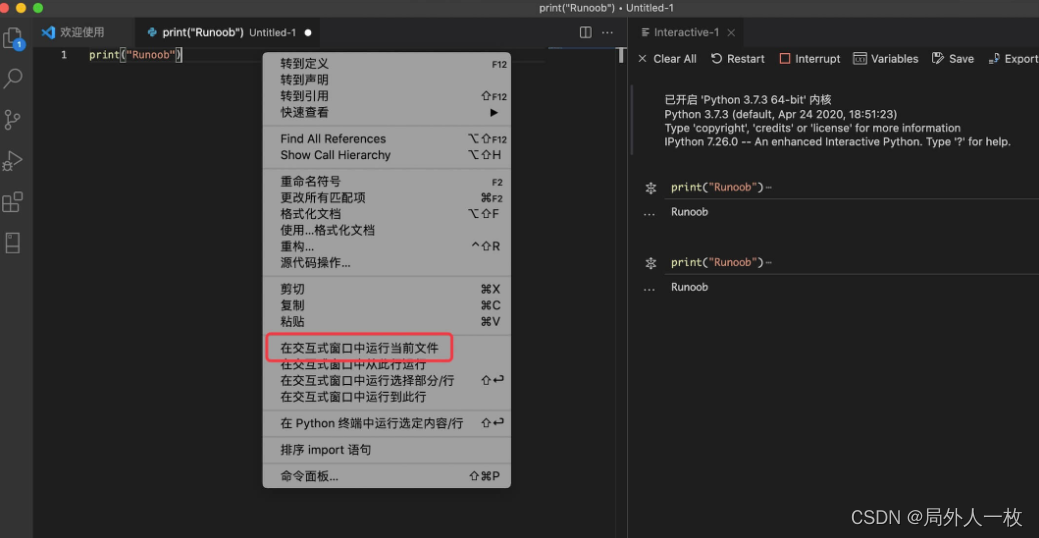
Python3 VScode 配置
Python3 VScode 配置 在上一章节中我们已经安装了 Python 的环境,本章节我们将介绍 Python VScode 的配置。 准备工作: 安装 VS Code 安装 VS Code Python 扩展 安装 Python 3 安装 VS Code VSCode(全称:Visual Studio Code&…...

VMware 修复了三个身份认证绕过漏洞
Bleeping Computer 网站披露,VMware 近期发布了安全更新,以解决 Workspace ONE Assist 解决方案中的三个严重漏洞,分别追踪为 CVE-2022-31685(认证绕过)、CVE-2022-31686 (认证方法失败)和 CVE-…...

实现一个简单的Database10(译文)
GreatSQL社区原创内容未经授权不得随意使用,转载请联系小编并注明来源。GreatSQL是MySQL的国产分支版本,使用上与MySQL一致。作者: 花家舍文章来源:GreatSQL社区原创 前文回顾 实现一个简单的Database系列 译注:csta…...
CTF-取证题目解析-提供环境
一、安装 官网下载:Volatility 2.6 Release 1、将windows下载的volatility上传到 kali/home 文件夹里面 3、将home/kali/vol刚刚上传的 移动到use/sbin目录里面 mv volatility usr/local/sbin/ 切换到里面 cd /usr/local/sbin/volatility 输入配置环境echo $PAT…...

计算机基础 | 网络篇 | TCP/IP 四层模型
前沿:撰写博客的目的是为了再刷时回顾和进一步完善,其次才是以教为学,所以如果有些博客写的较简陋,是为了保持进度不得已而为之,还请大家多多见谅。 一、OSI 七层模型 参考文章:OSI 和 TCP/IP 网络分层模型…...

实时数据仓库
1 为什么选择kafka? ① 实时写入,实时读取 ② 消息队列适合,其他数据库受不了 2 ods层 1)存储原始数据 埋点的行为数据 (topic :ods_base_log) 业务数据 (topic :ods_base_db) 2)业务数据的有序性&#x…...

leetcode 1250. 检查「好数组」
给你一个正整数数组 nums,你需要从中任选一些子集,然后将子集中每一个数乘以一个 任意整数,并求出他们的和。 假如该和结果为 1,那么原数组就是一个「好数组」,则返回 True;否则请返回 False。 示例 1&…...

JDK动态代理和CGLib动态代理的区别
原文网址:JDK动态代理和CGLib动态代理的区别_IT利刃出鞘的博客-CSDN博客 简介 本文介绍Java中JDK动态代理和CGLib动态代理的区别。 区别概述 项 JDK动态代理 CGLIB动态代理 接口是否需实现 只能代理实现了接口的类。 可以代理没有实现接口的类。 原理 继承…...

Leetcode.1250 检查「好数组」
题目链接 Leetcode.1250 检查「好数组」 Rating : 1983 题目描述 给你一个正整数数组 nums,你需要从中任选一些子集,然后将子集中每一个数乘以一个 任意整数,并求出他们的和。 假如该和结果为 1,那么原数组就是一个「…...

WMS系统推荐,如何选到适合企业的仓库管理系统
市场上有很多WMS系统,但是现在很多仓库管理系统都在使用WMS系统。那么在选择WMS系统时应该考虑什么呢?明确业务发展特征,准确表达能力目标许多物流企业在选择物流管理系统时,往往会被物流管理系统的整体系统所迷惑,在功…...
C语言的期末复习
🌈博客主页:卿云阁 💌欢迎关注🎉点赞👍收藏⭐️留言📝 🌟本文由卿云阁原创! 🙏作者水平很有限,如果发现错误,请留言轰炸哦!万分感谢&a…...

强化学习之DQN论文介绍
强化学习之DQN论文介绍DQN摘要介绍问题特点经验回放相关工作实验算法流程结论DQN 摘要 1.基于Q-learning从高维输入学习到控制策略的卷积神经网络。 2.输入是像素,输出是奖励函数。 3.主要训练、学习Atari 2600游戏,在6款游戏中3款超越人类专家。 介绍 …...

使用luaBridge添加自己的C++脚本插件能力
概述 如果我们有一个应用需要频繁的更改业务逻辑,但是基础功能不变,那么我们可以将基础功能作为底层接口,上层的功能按照脚本方式来编写。很多插件都这样的原理,比如我们的浏览器的JS就这样,小程序也是这样的原理,我们使用C++也很容易实现这样的功能。 lua是最小最精致的…...

DeepSeek 赋能智慧能源:微电网优化调度的智能革新路径
目录 一、智慧能源微电网优化调度概述1.1 智慧能源微电网概念1.2 优化调度的重要性1.3 目前面临的挑战 二、DeepSeek 技术探秘2.1 DeepSeek 技术原理2.2 DeepSeek 独特优势2.3 DeepSeek 在 AI 领域地位 三、DeepSeek 在微电网优化调度中的应用剖析3.1 数据处理与分析3.2 预测与…...

从WWDC看苹果产品发展的规律
WWDC 是苹果公司一年一度面向全球开发者的盛会,其主题演讲展现了苹果在产品设计、技术路线、用户体验和生态系统构建上的核心理念与演进脉络。我们借助 ChatGPT Deep Research 工具,对过去十年 WWDC 主题演讲内容进行了系统化分析,形成了这份…...

逻辑回归:给不确定性划界的分类大师
想象你是一名医生。面对患者的检查报告(肿瘤大小、血液指标),你需要做出一个**决定性判断**:恶性还是良性?这种“非黑即白”的抉择,正是**逻辑回归(Logistic Regression)** 的战场&a…...

PHP和Node.js哪个更爽?
先说结论,rust完胜。 php:laravel,swoole,webman,最开始在苏宁的时候写了几年php,当时觉得php真的是世界上最好的语言,因为当初活在舒适圈里,不愿意跳出来,就好比当初活在…...

测试markdown--肇兴
day1: 1、去程:7:04 --11:32高铁 高铁右转上售票大厅2楼,穿过候车厅下一楼,上大巴车 ¥10/人 **2、到达:**12点多到达寨子,买门票,美团/抖音:¥78人 3、中饭&a…...

三体问题详解
从物理学角度,三体问题之所以不稳定,是因为三个天体在万有引力作用下相互作用,形成一个非线性耦合系统。我们可以从牛顿经典力学出发,列出具体的运动方程,并说明为何这个系统本质上是混沌的,无法得到一般解…...

用docker来安装部署freeswitch记录
今天刚才测试一个callcenter的项目,所以尝试安装freeswitch 1、使用轩辕镜像 - 中国开发者首选的专业 Docker 镜像加速服务平台 编辑下面/etc/docker/daemon.json文件为 {"registry-mirrors": ["https://docker.xuanyuan.me"] }同时可以进入轩…...

多模态大语言模型arxiv论文略读(108)
CROME: Cross-Modal Adapters for Efficient Multimodal LLM ➡️ 论文标题:CROME: Cross-Modal Adapters for Efficient Multimodal LLM ➡️ 论文作者:Sayna Ebrahimi, Sercan O. Arik, Tejas Nama, Tomas Pfister ➡️ 研究机构: Google Cloud AI Re…...

第 86 场周赛:矩阵中的幻方、钥匙和房间、将数组拆分成斐波那契序列、猜猜这个单词
Q1、[中等] 矩阵中的幻方 1、题目描述 3 x 3 的幻方是一个填充有 从 1 到 9 的不同数字的 3 x 3 矩阵,其中每行,每列以及两条对角线上的各数之和都相等。 给定一个由整数组成的row x col 的 grid,其中有多少个 3 3 的 “幻方” 子矩阵&am…...

OPENCV形态学基础之二腐蚀
一.腐蚀的原理 (图1) 数学表达式:dst(x,y) erode(src(x,y)) min(x,y)src(xx,yy) 腐蚀也是图像形态学的基本功能之一,腐蚀跟膨胀属于反向操作,膨胀是把图像图像变大,而腐蚀就是把图像变小。腐蚀后的图像变小变暗淡。 腐蚀…...
