leetcode 困难 —— 数字 1 的个数(简单逻辑题)
(害,做题是真的慢,这面试给我这题我估计就傻了)
题目:
给定一个整数 n,计算所有小于等于 n 的非负整数中数字 1 出现的个数。
题解:
首先看看整数范围 0 <= n <= 10^9 不能遍历(不过这也肯定不会简单到遍历)
比如存在一个数 25103,我们应该从哪里下手呢
我们是否可以考虑,各个位置上(个位,十位…)存在 1 的情况数量,然后相加得到结果呢
我们先考虑一般情况, 数字 xxx 4 yy,百位上,存在 1 的情况数量怎么算
想一想 100,101,102,…,199是不是百位上都是 1,这种情况 100 种
在考虑一下百位前面的 xxx,是不是总共有 (xxx + 1) * 100 种
(假设 xxx 是 123,那么 123 1 yy 有 100 种,122 1 yy 有 100 种 … 000 1 yy 有 100 种)
接下来稍微扩展一下一般情况,那数字 xxxx 4 y 十位上的情况是不是就是 (xxxx + 1) * 10 种
接下来考虑特殊情况,如果数字 xxx 1 yy 百位上是 1,这怎么算呢
当前面是 xxx 时,百位上为 1 的情况只有 yy 种,但是当前面是 (xxx - n) 时,情况有 100 种
所以是不是情况是 xxx * 100 + yy 种
(假设 xxx 是 123,那么 123 1 yy 有 yy种,但 122 1 yy,则没有这种限制,有 100 种)
再一种特殊情况,如果数字 xxx 0 yy 百位上是 0,这怎么算呢
其实就是当前面是 xxx 时,百位上为 1 的情况为 0 种,当前面是 (xxx - n) 时,情况也都有 100 种
所以情况是 xxx * 100 种
接下来写代码就行了
class Solution {
public:int countDigitOne(int n) {int res = 0;int f = 1;int nn = n / 10;while(nn != 0) {nn = nn / 10;f = f * 10;}int flag = 0;while(f != 0) {int t = n / f;n = n % f;if(t == 1) {res = res + n + 1 + flag * f;}else if(t == 0) {res = res + flag * f;}else {res = res + (flag + 1) * f;}flag = flag * 10 + t;f = f / 10;}return res;}
};
相关文章:
)
leetcode 困难 —— 数字 1 的个数(简单逻辑题)
(害,做题是真的慢,这面试给我这题我估计就傻了) 题目: 给定一个整数 n,计算所有小于等于 n 的非负整数中数字 1 出现的个数。 题解: 首先看看整数范围 0 < n < 10^9 不能遍历࿰…...

关于JSON
<!DOCTYPE html> <html> <head> <meta charset"utf-8"> <title></title> </head> <body> <script> /* 1、JSON的英文全称:Java…...
Apifox-接口调用、自动化测试工具
Apifox简介 Apifox 的定位是Postman Swagger Mock JMeter,具有API文档管理、API调试、API Mock、API 自动化测试等功能。可以通过一种工具解决之前使用多种工具的数据同步问题。高效、及时、准确! 安装 Apifox的安装非常方便,直接下载安…...
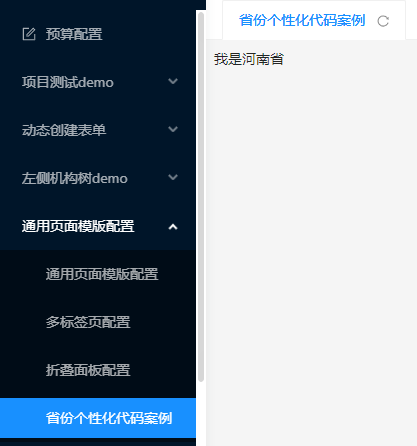
Vue一个项目兼容每个省份的个性化需求
开发环境及打包指令 后拼上省份区划"serve:henan": "yarn && vue-cli-service serve -o --encryptSM2 --zone41","serve:hunan": "yarn && vue-cli-service serve -o --encryptSM2 --zone43","serve:guizhou&quo…...

npm install报错 npm ERR! 的解决办法
以下是四种常见的npm ERR及解决方式错误一、npm ERR! A complete log of this run can be found in:npm ERR!C:\Users\nanyi\AppData\Roaming\npm-cache_logs\2021-09-17T08_58_23_413Z-debug.l查看错误日志,错误日志就在上面展示的C:\Users…这里如果发现错误日志里…...
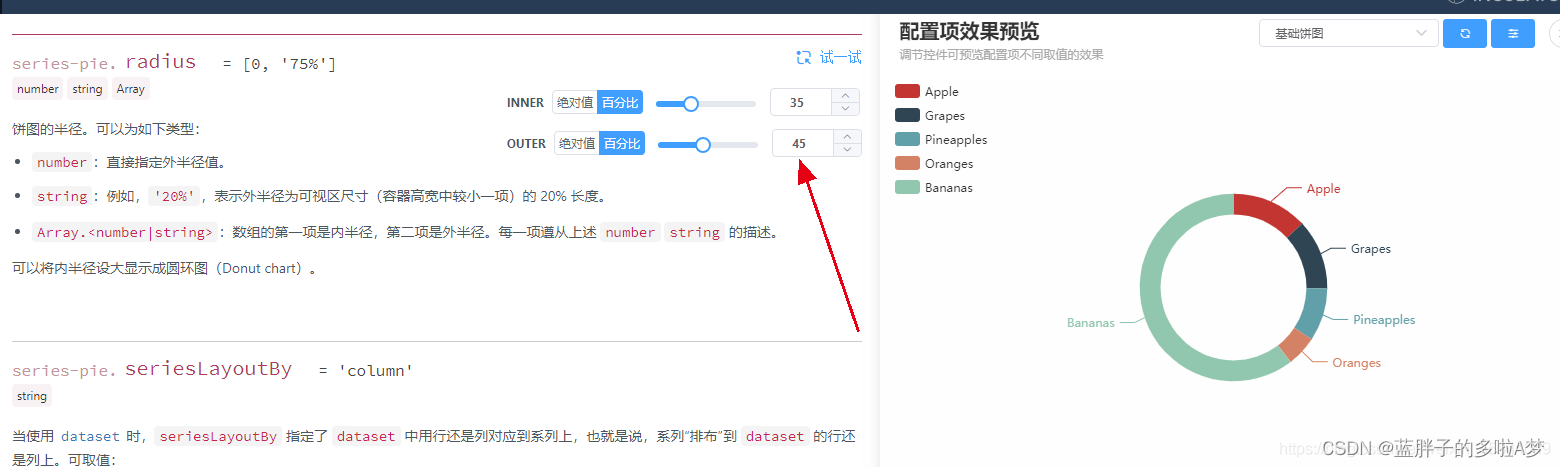
echarts修改饼图,环形图的圆环宽度,大小
echarts修改环形图的圆环宽度,大小 环形图圆环的大小需要通过series-pie. radius属性来修改 radius 饼图的半径。 Array.<number|string>:数组的第一项是内半径,第二项是外半径。每一项遵从上述 number string 的描述。 把数组的第…...

小白系列Vite-Vue3-TypeScript:010-封装svg
上一篇我们介绍了ViteVue3TypeScript项目中mockjs的安装和配置i。本篇我们来介绍封装SVG图标组件。svg特征Preloading所有图标都是在项目运行时生成的,只需要操作一次dom即可。高性能内置缓存,仅在文件被修改时才会重新生成。安装插件vite-plugin-svg-ic…...

卷严重、难度高、激励少,如何适应空投市场新变化
自从空投交互从2020年开始之后,不少人都开始加入到空投交互的行列中,一些项目也因为“格局”的因素,在项目正式上线前都会给早期参与者空投代币,以此吸引大家的关注。但是在越来越多的人加入到撸空投行列之中后,现在整…...

基于Java与JSP的文件上传和下载
概念 当用户在前端页面点击文件上传后,用户上传的文件数据提交给服务器端,实现保存。 文件上传步骤 提交方式: 提供form表单,method必须是post。因为post请求无数据限制。 <form method"post"></form>…...
Gromacs中的g_mmpbsa计算带电底物与蛋白的结合能不准确
g_mmpbsa计算带电底物与蛋白的结合能总是不准确 TOC 在做的两个项目中,利用g_mmpbsa计算带电底物与蛋白的结合能结果非常不可靠,底物带两个硫酸根离子,g_mmpbsa在计算带电的底物与酶的结合能时总是不准确,因此后续若底物带电&…...
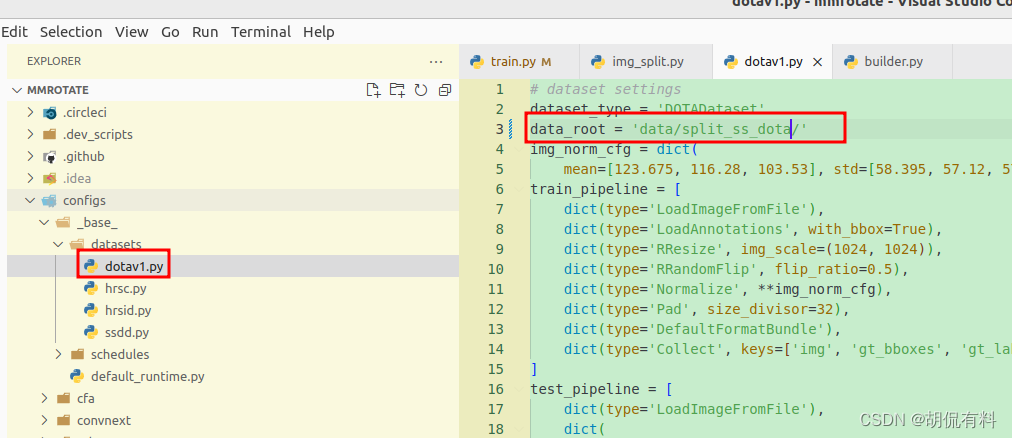
【mmrotate】旋转目标检测之训练DOTA数据集
every blog every motto: You can do more than you think. https://blog.csdn.net/weixin_39190382?typeblog 0. 前言 mmrotate训练DOTA数据集记录 1. 正文 1.1 数据准备 数据介绍部分,参考DOTA数据介绍,官方提供了裁剪工具development kit。这里…...

图基本概念
图:顶点和边的集合。无向图:每条边都是无方向的有向图:每条边都是有方向的完全图:任意两个点都有一条边相连稀疏图:有很少边或弧的图稠密图:有较多边或弧的图网:边/弧带权的图邻接:有…...
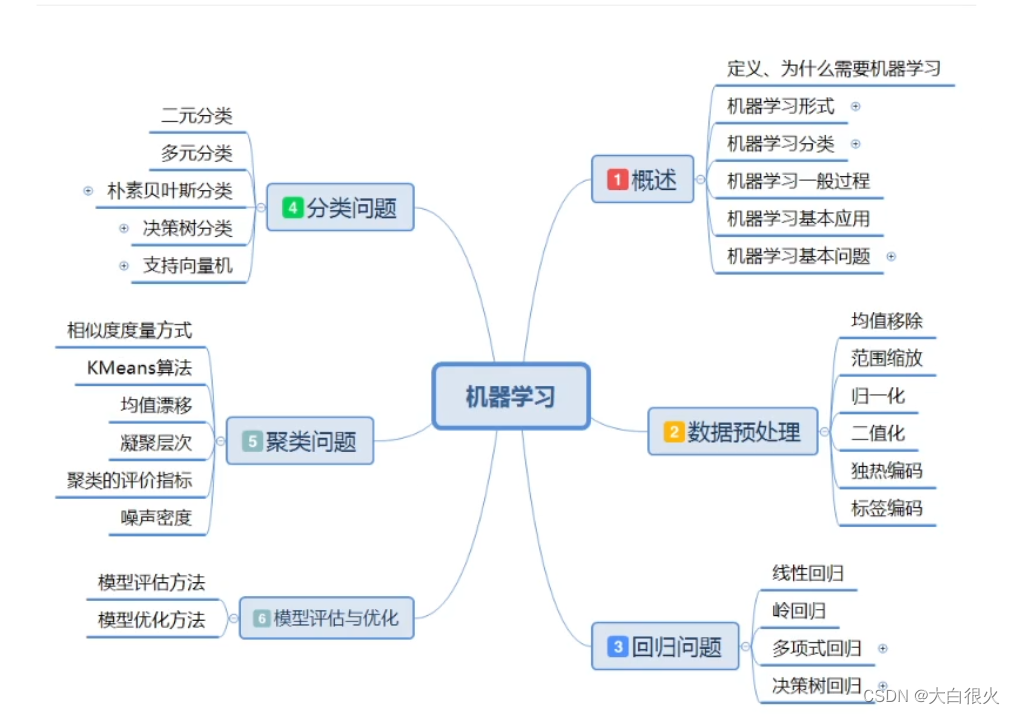
机器学习基础
一、基本概念 1 学习的概念 1975年图灵奖获得者、1978年诺贝尔经济学奖获得者、著名学者赫伯特.西蒙 (Herbert Simon) 曾下过一个定义: 如果一个系统,能够通过执行某个过程,就此改进了它的性能,那么这个过程就是学习.由此可看出,…...

FreeRTOS-Tickless低功耗模式 | FreeRTOS十四
目录 说明: 一、低功耗模式简介 1.1、STM32低功耗模式 二、Tickless模式 2.1、Tickless模式如何功耗 2.2、Tickless模式设计思想 2.3、为了降低功耗,又不影响系统运行,怎么能做到呢? 三、Tickless模式修改配置 3.1、配置…...
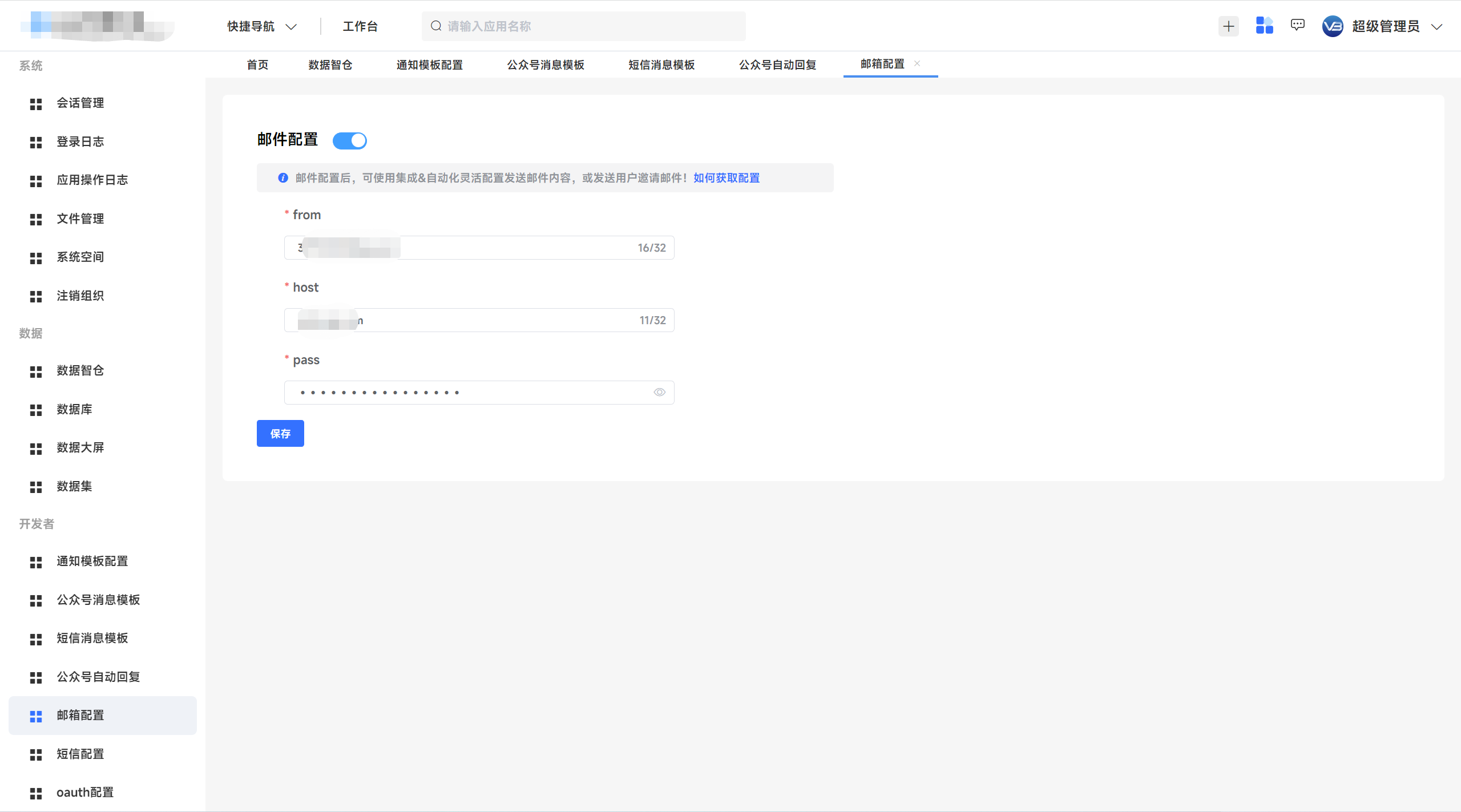
实现了统一消息中心的微服务基础框架 JVS,快点赞收藏
一、开源项目简介基于JVS(基于spring cloud封装)的基础开源框架,实现了基于多对多租户能力的管理系统。二、基础框架实现功能支持数据管理支持分布式定时任务支持分布式日志采集支持系统监控支持动态配置中心支持模板消息支持链路跟踪支持邮件…...

VMware 安装 OpenWrt 旁路由并配置 PassWall
1、准备 OpenWrt 镜像包 我已经转好了 vmdk 格式的,更多的可以去恩山论坛下载 OpenWrtvmdk格式-虚拟化文档类资源-CSDN下载 也可以在这个平台在线定制 OpenWrt固件下载与在线定制编译 2、网络选择 NAT 模式 3、创建虚拟机,选择自定义方式 4、一直下…...

R语言GD包地理探测器分析时报错、得不到结果等情况的解决方案
本文介绍在利用R语言的GD包,实现自变量最优离散化方法选取与执行、地理探测器(Geodetector)操作时,出现各类报错信息、长时间得不到结果等情况的解决方案。 在之前的文章R语言GD包基于栅格图像实现地理探测器与连续参数的自动离散…...

嵌入式开发:你需要知道的5种简单
传达嵌入式软件体系结构设计意图通常伴随着基于嵌入式开发人员经验的假设。你可以从资源受限的基于微控制器的系统的角度来看架构设计。如何设计架构将取决于系统的嵌入式软件分类。有许多不同的方法可以对嵌入式软件进行分类。我发现有五种简单的嵌入式软件分类可以帮助我调整…...
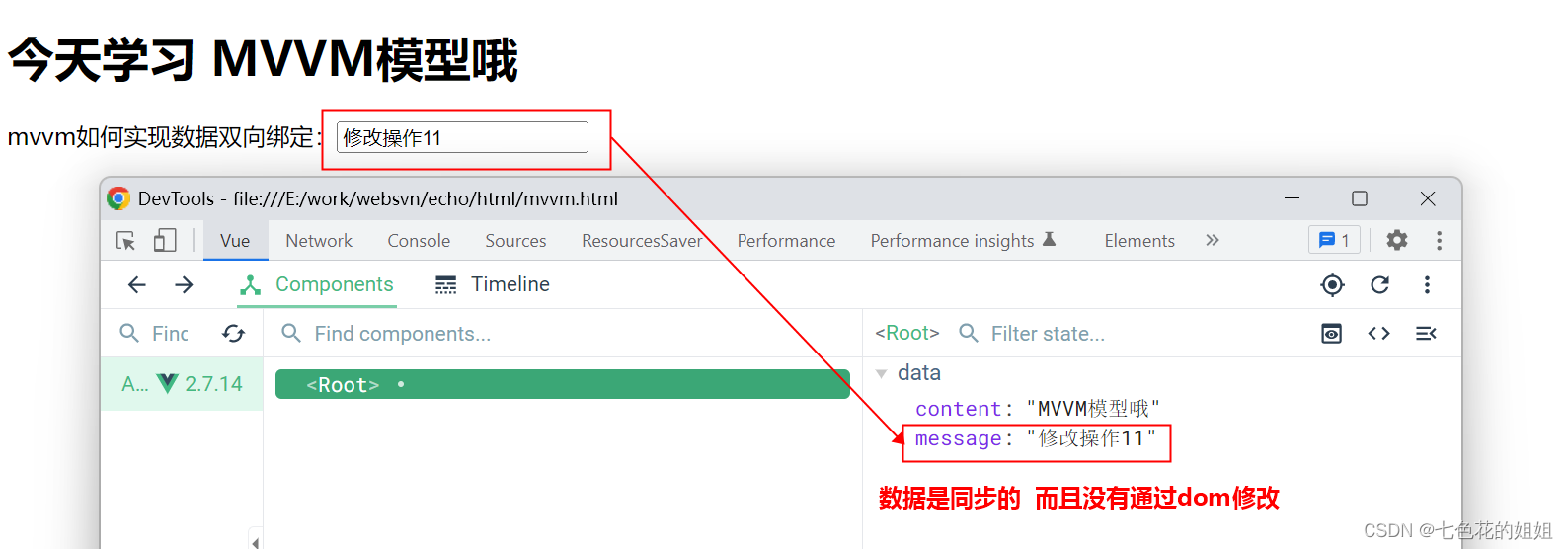
MVC与MVVM
MVC与MVVM举例说明MVCMVVM两者比较MVC <!DOCTYPE html> <html><head><meta charset"utf-8"><meta http-equiv"X-UA-Compatible" content"IEedge"><title>mvc案例</title><link rel"styleshe…...
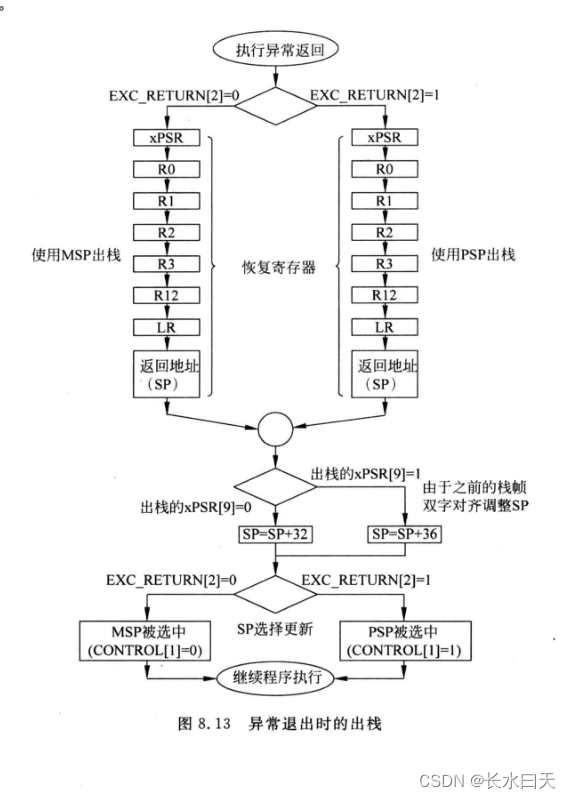
Cortex-M0异常和中断
目录1.概念2.异常类型3.异常优先级定义4.向量表5.异常流程概述接受异常请求压栈和出栈异常返回指令末尾连锁延迟到达6.EXC_RETURN7.异常入口流程的细节压栈取出向量并更新PC寄存器更新8.异常退出流程的细节1.概念 异常是能够引起程序流偏离正常流程的事件,当异常发…...

盘古信息PCB行业解决方案:以全域场景重构,激活智造新未来
一、破局:PCB行业的时代之问 在数字经济蓬勃发展的浪潮中,PCB(印制电路板)作为 “电子产品之母”,其重要性愈发凸显。随着 5G、人工智能等新兴技术的加速渗透,PCB行业面临着前所未有的挑战与机遇。产品迭代…...

定时器任务——若依源码分析
分析util包下面的工具类schedule utils: ScheduleUtils 是若依中用于与 Quartz 框架交互的工具类,封装了定时任务的 创建、更新、暂停、删除等核心逻辑。 createScheduleJob createScheduleJob 用于将任务注册到 Quartz,先构建任务的 JobD…...

【ROS】Nav2源码之nav2_behavior_tree-行为树节点列表
1、行为树节点分类 在 Nav2(Navigation2)的行为树框架中,行为树节点插件按照功能分为 Action(动作节点)、Condition(条件节点)、Control(控制节点) 和 Decorator(装饰节点) 四类。 1.1 动作节点 Action 执行具体的机器人操作或任务,直接与硬件、传感器或外部系统…...

TRS收益互换:跨境资本流动的金融创新工具与系统化解决方案
一、TRS收益互换的本质与业务逻辑 (一)概念解析 TRS(Total Return Swap)收益互换是一种金融衍生工具,指交易双方约定在未来一定期限内,基于特定资产或指数的表现进行现金流交换的协议。其核心特征包括&am…...

零基础设计模式——行为型模式 - 责任链模式
第四部分:行为型模式 - 责任链模式 (Chain of Responsibility Pattern) 欢迎来到行为型模式的学习!行为型模式关注对象之间的职责分配、算法封装和对象间的交互。我们将学习的第一个行为型模式是责任链模式。 核心思想:使多个对象都有机会处…...

selenium学习实战【Python爬虫】
selenium学习实战【Python爬虫】 文章目录 selenium学习实战【Python爬虫】一、声明二、学习目标三、安装依赖3.1 安装selenium库3.2 安装浏览器驱动3.2.1 查看Edge版本3.2.2 驱动安装 四、代码讲解4.1 配置浏览器4.2 加载更多4.3 寻找内容4.4 完整代码 五、报告文件爬取5.1 提…...

GC1808高性能24位立体声音频ADC芯片解析
1. 芯片概述 GC1808是一款24位立体声音频模数转换器(ADC),支持8kHz~96kHz采样率,集成Δ-Σ调制器、数字抗混叠滤波器和高通滤波器,适用于高保真音频采集场景。 2. 核心特性 高精度:24位分辨率,…...

docker 部署发现spring.profiles.active 问题
报错: org.springframework.boot.context.config.InvalidConfigDataPropertyException: Property spring.profiles.active imported from location class path resource [application-test.yml] is invalid in a profile specific resource [origin: class path re…...

人工智能(大型语言模型 LLMs)对不同学科的影响以及由此产生的新学习方式
今天是关于AI如何在教学中增强学生的学习体验,我把重要信息标红了。人文学科的价值被低估了 ⬇️ 转型与必要性 人工智能正在深刻地改变教育,这并非炒作,而是已经发生的巨大变革。教育机构和教育者不能忽视它,试图简单地禁止学生使…...

【SSH疑难排查】轻松解决新版OpenSSH连接旧服务器的“no matching...“系列算法协商失败问题
【SSH疑难排查】轻松解决新版OpenSSH连接旧服务器的"no matching..."系列算法协商失败问题 摘要: 近期,在使用较新版本的OpenSSH客户端连接老旧SSH服务器时,会遇到 "no matching key exchange method found", "n…...
