【SPSS】频数分析和基本描述统计量详细操作教程(附实战案例)

🤵♂️ 个人主页:@艾派森的个人主页
✍🏻作者简介:Python学习者
🐋 希望大家多多支持,我们一起进步!😄
如果文章对你有帮助的话,
欢迎评论 💬点赞👍🏻 收藏 📂加关注+
目录
频数分析
频数分析案例
SPSS频数分析的扩展功能
基本描述统计量
计算基本描述统计量应用
频数分析
频数分析的目的
基本统计分析往往从频数分析开始。通过频数分析能够了解变量的取值状况,对把握数据的分布特征是非常有用的。
频数分析的基本任务
1.编制频数分布表
- 频数:变量值落在某个区间(或某个类别)中的次数
- 百分比:各频数占总样本量的百分比
- 有效百分比:各频数占总有效样本量的百分比 累计百分比
2.绘制统计图
- 条形图
- 饼图
- 频数直方图:用矩形的面积来表示频数
频数分析案例
 【案例】: 利用大学生职业生涯规划数据,分析被调查者的专业分布状 况,以及参加规划课程指 导(Q3)的情况。
【案例】: 利用大学生职业生涯规划数据,分析被调查者的专业分布状 况,以及参加规划课程指 导(Q3)的情况。
操作步骤:
①选择菜单【分析】----> 【描述统计】----> 【频率】
②选择“专业分类”和“规划课程指导”到变量(V)中
③点击上图的"图表"按钮选择绘制统计图形
④分别点击继续、确定,最终的编制频数分布表与直方图
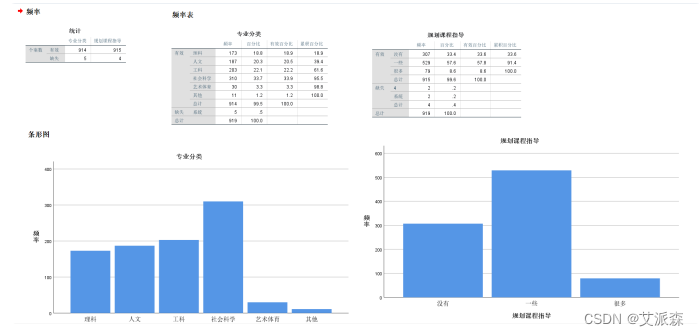
SPSS频数分析的扩展功能

频数分析的扩展功能
计算分位数:分位数是变量在不同分位点上的取值。分位点在0~100之间。一 般使用较多的是四分位点,即将所有数据按升序排序后平均等分 成四份,各分位点依次是25%,50%,75%。于是,四分位数分别是 25%,50%,75%分位点对应的变量值,依次称为下四分位数、中位 数和上四分位数。
计算其他基本描述统计量:描述集中趋势的基本统计量、描述离散程度的基本统计量、描述 分布形态的基本统计量。
【案例】 利用大学生职业生涯规划数据,分析专业和职业认知得分的分布
①选择菜单【分析】----> 【描述统计】----> 【频率】
②如下图,选择X1变量(Q61+Q62+Q63+Q64,也即“专业和职业认知得分”)点击“统计”按钮,在出现的统计对话框中再勾选“四分 位数”选项
③点击下图的"图表"按钮选择绘制直方图,并在直方图中显示正态曲线
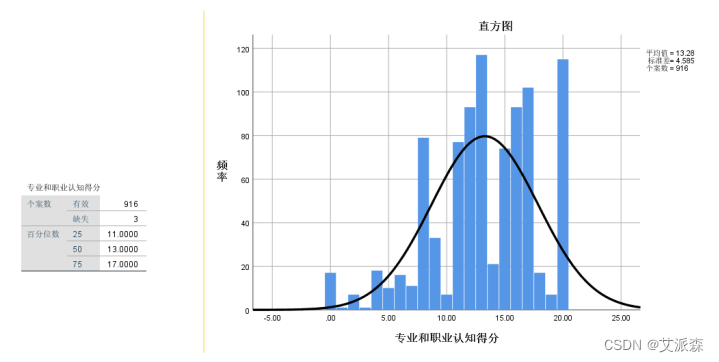
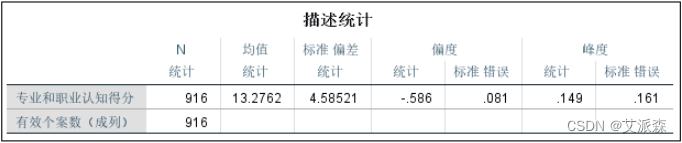
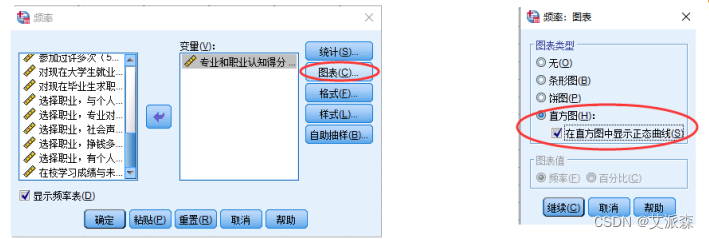 ④分别点击“继续”、“确定”,分析结果如下
④分别点击“继续”、“确定”,分析结果如下
 基本描述统计量
基本描述统计量

刻画集中趋势的描述统计量
刻画集中趋势的描述统计量是能够反映一般水平的“代表值”或“中心值”
- 均值
- 中位数
- 众数
重抽样自举法:
- 将已有的n个观测数据看做能够从中抽取的总体。若从中有放回地随机抽取n个数据形成一个 样本(称为自举样本),便可计算得到一个样本统计量(如样本均值)。该过程称为重抽样自举过程
- 如果重抽样自举过程反复进行m次,便可得到m个样本统计量
- SPSS提供的Bootstrap按钮能够自动完成重抽样自举过程
刻画离散程度的描述统计量
离散程度是指一组数据远离其中心值的程度。中心值和关于中 心值的离散程度共同作用才能给出对数据比较全面完整的描述。
- 样本标准差:样本标准差是对变量取值距均值的平均离散程度的估计。样本标准差是有计量单位的。
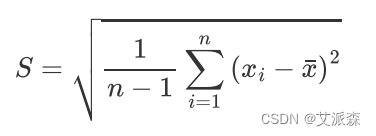
- 样本方差:样本方差没有计量单位。
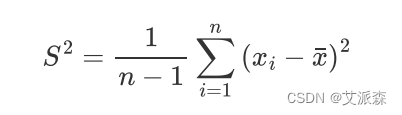
- 全距(极差):数据的最大值与最小值之间的绝对差
刻画分布形态的描述统计量
数据的分布形态主要指数据分布是否对称,偏斜程度如何,陡缓程度如何等。
- 偏度系数(Skewness):是描述变量取值分布形态对称性的统计量
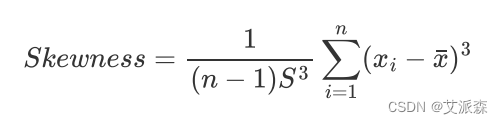
注意:
- 当分布是对称分布时,正负总偏差相等,偏度值等于0
- 偏度值小于0表示负偏或称左偏,直方图中有一条长尾拖在左边
- 偏度值大于0表示正偏或称右偏,直方图中有一条长尾拖在右边
- 偏度绝对值越大,表示数据分布形态的偏斜程度越大
- 峰度系数(Kurtosis):是描述变量取值分布形态陡缓程度的统计量
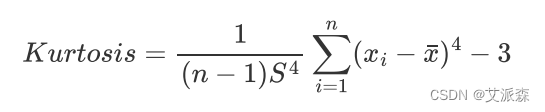
注意:
- 当数据分布与标准正态分布的陡缓程度相同时,峰度值等于0
- 峰度值大于0表示数据的分布比标准正态分布更陡峭,称为尖峰分布
- 峰度值小于0表示数据的分布比标准正态分布更平缓,称为平峰分布
计算基本描述统计量应用

【案例】 利用大学生职业生涯规划数据,计算专业和职业认知得分的基本描述统计量
①选择菜单【分析】----> 【描述统计】----> 【描述】
②选择需计算的数值型变量到【变量(V)】框中,这里选择“专业和职业认知得分”
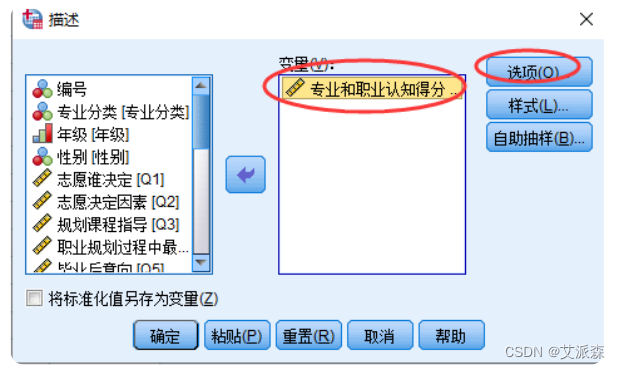
③点击上图的“选项”按钮指定计算哪些基本描述统计量
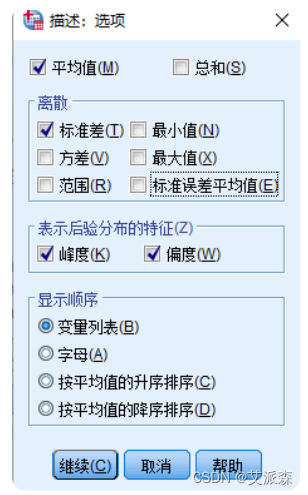
④最终分析结果
相关文章:

【SPSS】频数分析和基本描述统计量详细操作教程(附实战案例)
🤵♂️ 个人主页:艾派森的个人主页 ✍🏻作者简介:Python学习者 🐋 希望大家多多支持,我们一起进步!😄 如果文章对你有帮助的话, 欢迎评论 💬点赞Ǵ…...
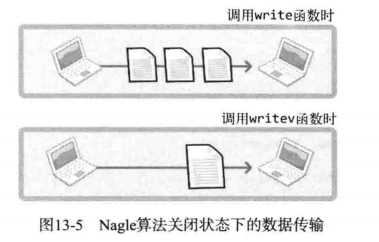
TCP/IP网络编程——多种 I/O 函数
完整版文章请参考: TCP/IP网络编程完整版文章 文章目录第 13 章 多种 I/O 函数13.1 send & recv 函数13.1.1 Linux 中的 send & recv13.1.2 MSG_OOB:发送紧急消息13.1.3 紧急模式工作原理13.1.4 检查输入缓冲13.2 readv & writev 函数13.2.1…...

静态代理和动态代理的区别以及实现过程
前言 代理模式是一种设计模式,能够使得在不修改源目标的前提下,额外扩展源目标的功能。即通过访问源目标的代理类,再由代理类去访问源目标。这样一来,要扩展功能,就无需修改源目标的代码了。只需要在代理类上增加就可…...
Consul SpringCloudK8S
背景说起微服务,就需要用到SpringCloud,目前市面上主流的SpringCloud产品有这些:SpringCloudNeflix、Spring Cloud Alibaba、Spring Cloud for AWS、Spring Cloud Azure 和 Spring Cloud Kubernetes。其中SpringCloudNeflix已经不在更新&…...

anaconda3文件夹被移动之后,如何操作可以复用原有conda环境
anaconda3文件夹被移动A-调整conda PATH地址B-更改.conda/environments.txt中的地址C-修改conda内的变量和每个环境的pip目录A-调整conda PATH地址 B-更改.conda/environments.txt中的地址 a. 优先切换到用户根目录 b. 查看隐藏conda目录 c. 编辑 vi .conda/environments.txt…...
 Queue(单向队列) Deque(双向队列))
【Java】Stack(栈) Queue(单向队列) Deque(双向队列)
Stack (栈) Stack 是一个先进后出的栈,可以将其理解为一个只开了一个口子的管子,放进去的东西只能从这一个口进出。所以先放进去的元素在取出的时候只能到最后才能取出来。 Stack具备一下几个方法: boolean empty() …...

自定义spring拦截器
说明: 一些版本比较老的spring框架的,是通过继承HandlerInterceptorAdapter并重写preHandle()方法,和继承WebMvcConfigurerAdapter并重写 addInterceptors()方法来实现拦截器的,但是这两个类很久前就已经过时了,不推荐…...

今天正式上线!虹科汽车免拆诊断云展厅:感受精准修车魅力,畅享汽修领先技术
『虹科汽车免拆诊断云展厅』 2月15日正式上线! 在这里,您可以参观了解: 虹科Pico汽车示波器产品模型 全流程专业讲解的视频资料 产品功能和应用场景 全面详细的产品手册 还有虹科首席技术工程师在线连麦答疑!!…...

4.数据类型-字符串【Python】
文章目录字符串索引切片转义字符格式化符号f-string字符串操作判断&检测转换剪切&填充拼接统计格式转化练习字符串 字符串是 Python 中最常用的数据类型。可以使用单引号,双引号,3对双引号创建一个字符串。Python 中没有单独的字符类型 char…...
:A股股票列表免费抓取实战)
搞量化先搞数(上):A股股票列表免费抓取实战
到了这一步,我们学习了基础的爬虫请求库urllib和requests,尤其是后者,强大且易用,极其适合新手使用。那么今天我们就找一个相对简单的案例,来看一下如何在实战中应用爬虫技能。 相信很多朋友都对股票感兴趣,甚至有些朋友想要通过量化研究来获得超额收益。然而,想要进行…...

SpringCloud-负载均衡Ribbon
一、配置使用1、添加依赖(该依赖包含在eureka-client依赖中)<dependency><groupId>org.springframework.cloud</groupId><artifactId>spring-cloud-starter-netflix-ribbon</artifactId></dependency>2、在RestTemp…...
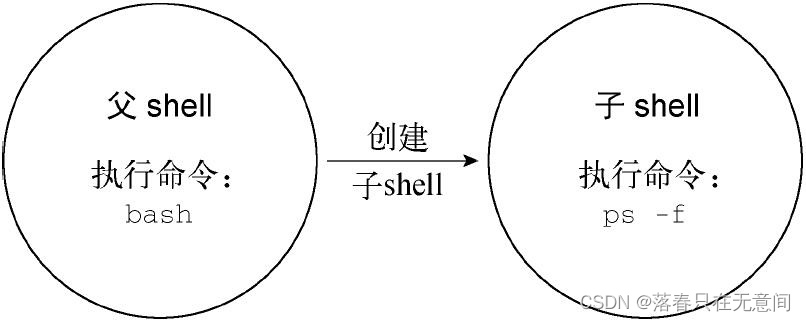
Linux入门篇(二)
Linux前言链接文件符号链接(软链接)硬链接shellshell 的类型shell的父子关系理解外部命令和内建命令外部命令内建命令Linux环境变量PATH环境变量前言 在这一章,我对Linux中有关shell较为深入的理解和环境变量方面知识的一个记录。同时&#x…...

第四部分:特殊用途的句子——第三章:虚拟
虚拟语气 1、什么是虚拟? 虚拟就是非真实。换句话说,这事不是真的,这事不太可能成真,非真实,就是虚拟 2、怎么表示虚拟? 英语是一个典型的形式来补充内容的语言,若要表达虚拟,只…...

Java中如何获取泛型类型信息
文章目录声明侧泛型使用侧泛型获取泛型类型相关方法1. Class类的泛型方法2. Field类的泛型方法3. Method类的泛型方法4. ParameterizedType类获取声明侧的泛型类型信息获取使用侧的泛型类型信息匿名内部类实现获取使用侧的泛型类型根据使用泛型位置的不同可以分为:声…...
【云原生】centos7搭建安装k8s集群 v1.25版本详细教程实战
文章目录前言一. 实验环境二. k8s 的介绍三 . k8s的安装3.1 搭建实验环境3.1.1 硬件层面的要求3.1.2 软件层面环境配置3.2 docker的安装3.2.1 搭建docker3.2.2 部署 cri-dockerd3.3 部署k8s3.3.1 配置添加阿里云的yum源3.3.2 安装kubeadm kubelet kubectl3.3.3 k8s-master节点初…...
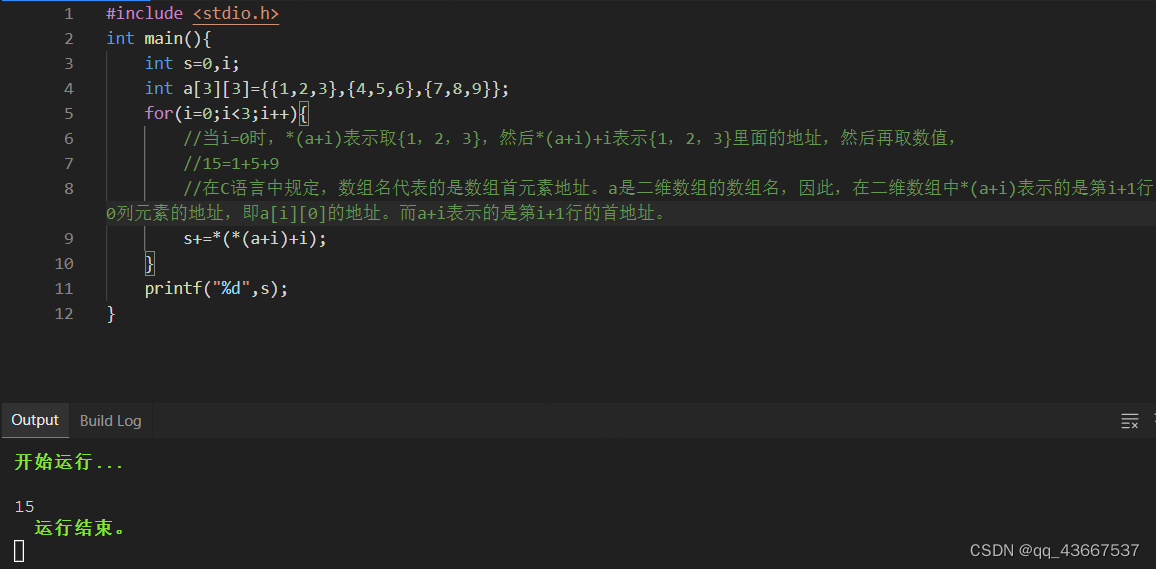
c语言指针
指针 指针是存放地址的变量,也可以说指针地址。 对于定义p(这里的话,只是定义,说明p是指针),p作为一个指针去指向存放数据的位置,而p意思是取(p指向的内存位置的数据)&…...

5.33 综合案例2.0 -ESP32拍照上传阿里云OSS
综合案例2.0 - ESP32拍照上传阿里云OSS案例说明连线功能实现1.阿里云平台连接2.OSS对象存储服务3.ESP32-CAM开发环境4.代码ESP32-CAM开发板代码HaaS506开发板代码测试数据转图片方法案例说明 使用ESP32拍照,将照片数据上传阿里云OSS(通过4G网络上传)。 …...
java无重复字符的最长子串
给定一个字符串 s ,请你找出其中不含有重复字符的 最长子串 的长度。 示例 1: 输入: s “abcabcbb” 输出: 3 解释: 因为无重复字符的最长子串是 “abc”,所以其长度为 3。 示例 2: 输入: s “bbbbb” 输出: 1 解释: 因为无重复字符的最长子串是 “…...

测试用例设计工作中的应用
1. 等价类划分 常见的软件测试面试题划分等价类: 等价类是指某个输入域的子集合.在该子集合中,各个输入数据对于揭露程序中的错误都是等效的.并合理地假定:测试某等价类的代表值就等于对这一类其它值的测试.因此,可以把全部输入数据合理划分为假设干等价类,在每一个等价类中取一…...
)
leetcode 困难 —— 数字 1 的个数(简单逻辑题)
(害,做题是真的慢,这面试给我这题我估计就傻了) 题目: 给定一个整数 n,计算所有小于等于 n 的非负整数中数字 1 出现的个数。 题解: 首先看看整数范围 0 < n < 10^9 不能遍历࿰…...

铭豹扩展坞 USB转网口 突然无法识别解决方法
当 USB 转网口扩展坞在一台笔记本上无法识别,但在其他电脑上正常工作时,问题通常出在笔记本自身或其与扩展坞的兼容性上。以下是系统化的定位思路和排查步骤,帮助你快速找到故障原因: 背景: 一个M-pard(铭豹)扩展坞的网卡突然无法识别了,扩展出来的三个USB接口正常。…...

【Python】 -- 趣味代码 - 小恐龙游戏
文章目录 文章目录 00 小恐龙游戏程序设计框架代码结构和功能游戏流程总结01 小恐龙游戏程序设计02 百度网盘地址00 小恐龙游戏程序设计框架 这段代码是一个基于 Pygame 的简易跑酷游戏的完整实现,玩家控制一个角色(龙)躲避障碍物(仙人掌和乌鸦)。以下是代码的详细介绍:…...
: K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?)
云原生核心技术 (7/12): K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?
大家好,欢迎来到《云原生核心技术》系列的第七篇! 在上一篇,我们成功地使用 Minikube 或 kind 在自己的电脑上搭建起了一个迷你但功能完备的 Kubernetes 集群。现在,我们就像一个拥有了一块崭新数字土地的农场主,是时…...

MongoDB学习和应用(高效的非关系型数据库)
一丶 MongoDB简介 对于社交类软件的功能,我们需要对它的功能特点进行分析: 数据量会随着用户数增大而增大读多写少价值较低非好友看不到其动态信息地理位置的查询… 针对以上特点进行分析各大存储工具: mysql:关系型数据库&am…...

大数据零基础学习day1之环境准备和大数据初步理解
学习大数据会使用到多台Linux服务器。 一、环境准备 1、VMware 基于VMware构建Linux虚拟机 是大数据从业者或者IT从业者的必备技能之一也是成本低廉的方案 所以VMware虚拟机方案是必须要学习的。 (1)设置网关 打开VMware虚拟机,点击编辑…...

使用van-uploader 的UI组件,结合vue2如何实现图片上传组件的封装
以下是基于 vant-ui(适配 Vue2 版本 )实现截图中照片上传预览、删除功能,并封装成可复用组件的完整代码,包含样式和逻辑实现,可直接在 Vue2 项目中使用: 1. 封装的图片上传组件 ImageUploader.vue <te…...
:爬虫完整流程)
Python爬虫(二):爬虫完整流程
爬虫完整流程详解(7大核心步骤实战技巧) 一、爬虫完整工作流程 以下是爬虫开发的完整流程,我将结合具体技术点和实战经验展开说明: 1. 目标分析与前期准备 网站技术分析: 使用浏览器开发者工具(F12&…...

【JavaWeb】Docker项目部署
引言 之前学习了Linux操作系统的常见命令,在Linux上安装软件,以及如何在Linux上部署一个单体项目,大多数同学都会有相同的感受,那就是麻烦。 核心体现在三点: 命令太多了,记不住 软件安装包名字复杂&…...

人工智能(大型语言模型 LLMs)对不同学科的影响以及由此产生的新学习方式
今天是关于AI如何在教学中增强学生的学习体验,我把重要信息标红了。人文学科的价值被低估了 ⬇️ 转型与必要性 人工智能正在深刻地改变教育,这并非炒作,而是已经发生的巨大变革。教育机构和教育者不能忽视它,试图简单地禁止学生使…...

【SSH疑难排查】轻松解决新版OpenSSH连接旧服务器的“no matching...“系列算法协商失败问题
【SSH疑难排查】轻松解决新版OpenSSH连接旧服务器的"no matching..."系列算法协商失败问题 摘要: 近期,在使用较新版本的OpenSSH客户端连接老旧SSH服务器时,会遇到 "no matching key exchange method found", "n…...

