用于非线性时间序列预测的稀疏局部线性和邻域嵌入(Matlab代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥
🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。
⛳️座右铭:行百里者,半于九十。
📋📋📋本文目录如下:🎁🎁🎁
目录
💥1 概述
📚2 运行结果
🎉3 参考文献
🌈4 Matlab代码实现
💥1 概述
“本文提出了一种基于字典的L1范数稀疏编码,用于时间序列预测,不需要训练阶段,参数调整最少,适用于非平稳和在线预测应用。预测过程被表述为基础追求 L1 范数问题,其中为每个测试向量估计一组稀疏权重。尝试了约束稀疏编码公式,包括稀疏局部线性嵌入和稀疏最近邻嵌入。16个时间序列数据集用于测试离线时间序列预测方法,其中训练数据是固定的。所提出的方法还与Bagging树(BT),最小二乘支持向量回归(LSSVM)和正则化自回归模型进行了比较。所提出的稀疏编码预测显示出比使用10倍交叉验证的LSSVM更好的性能,并且比正则化AR和Bagging树的性能明显更好。平均而言,在LSSVM训练时可以完成几千个稀疏编码预测。
📚2 运行结果
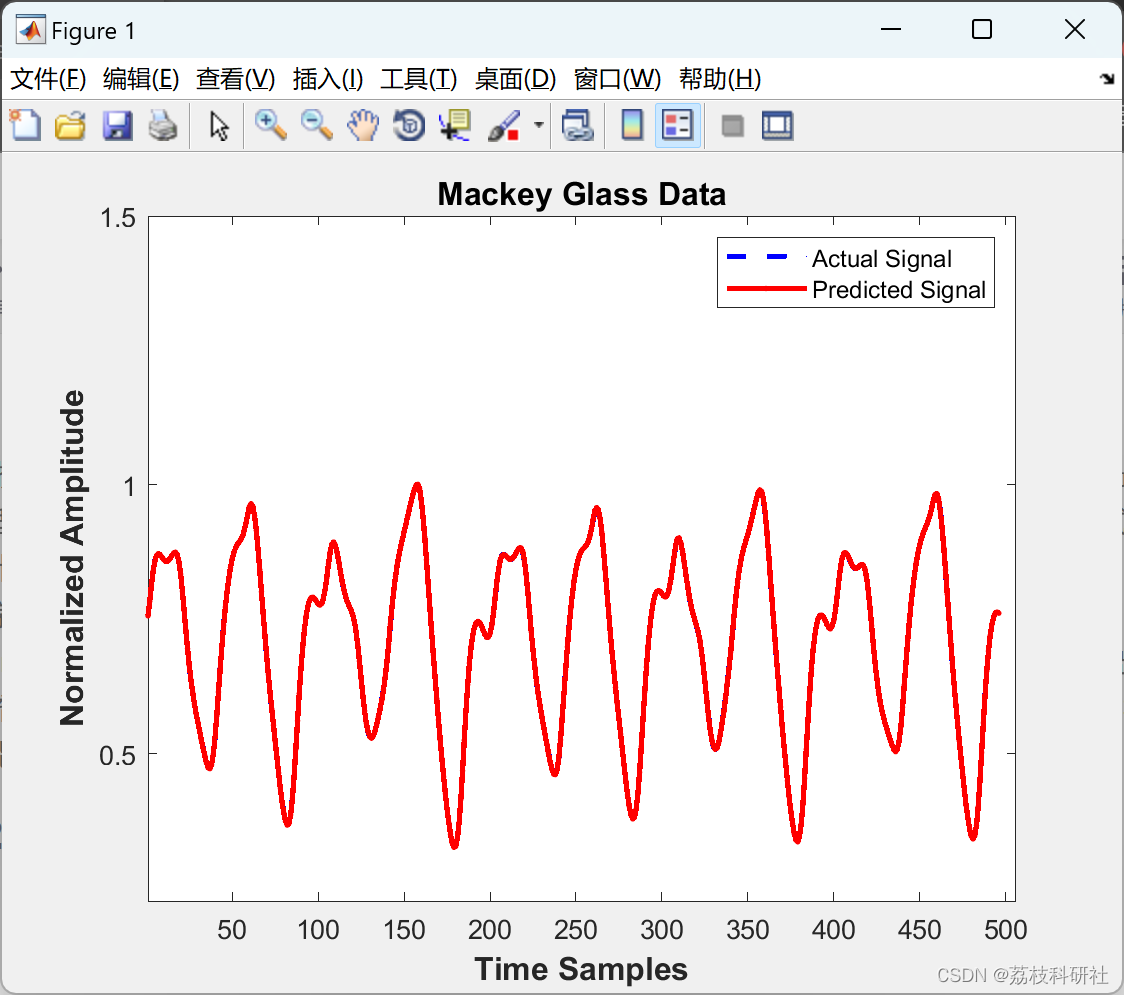
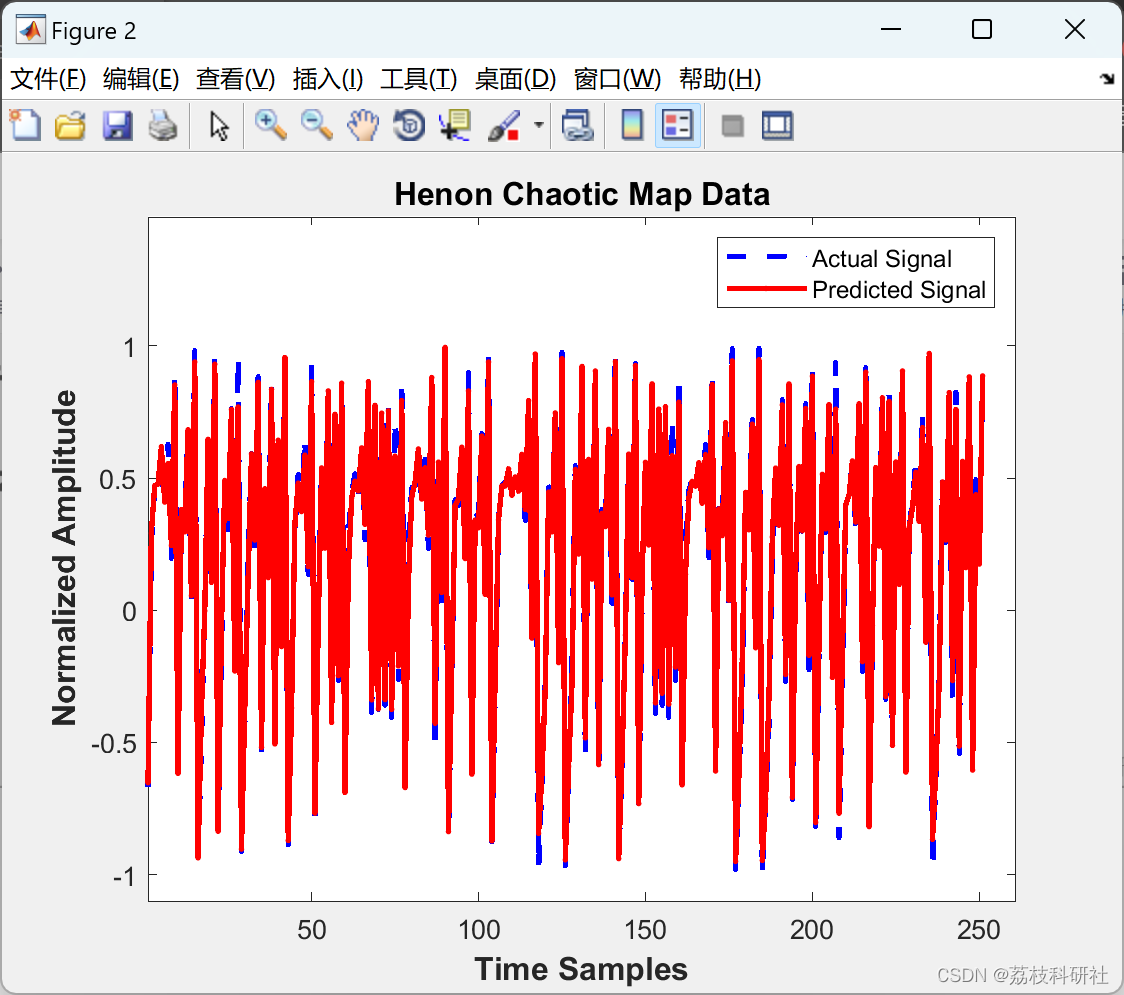
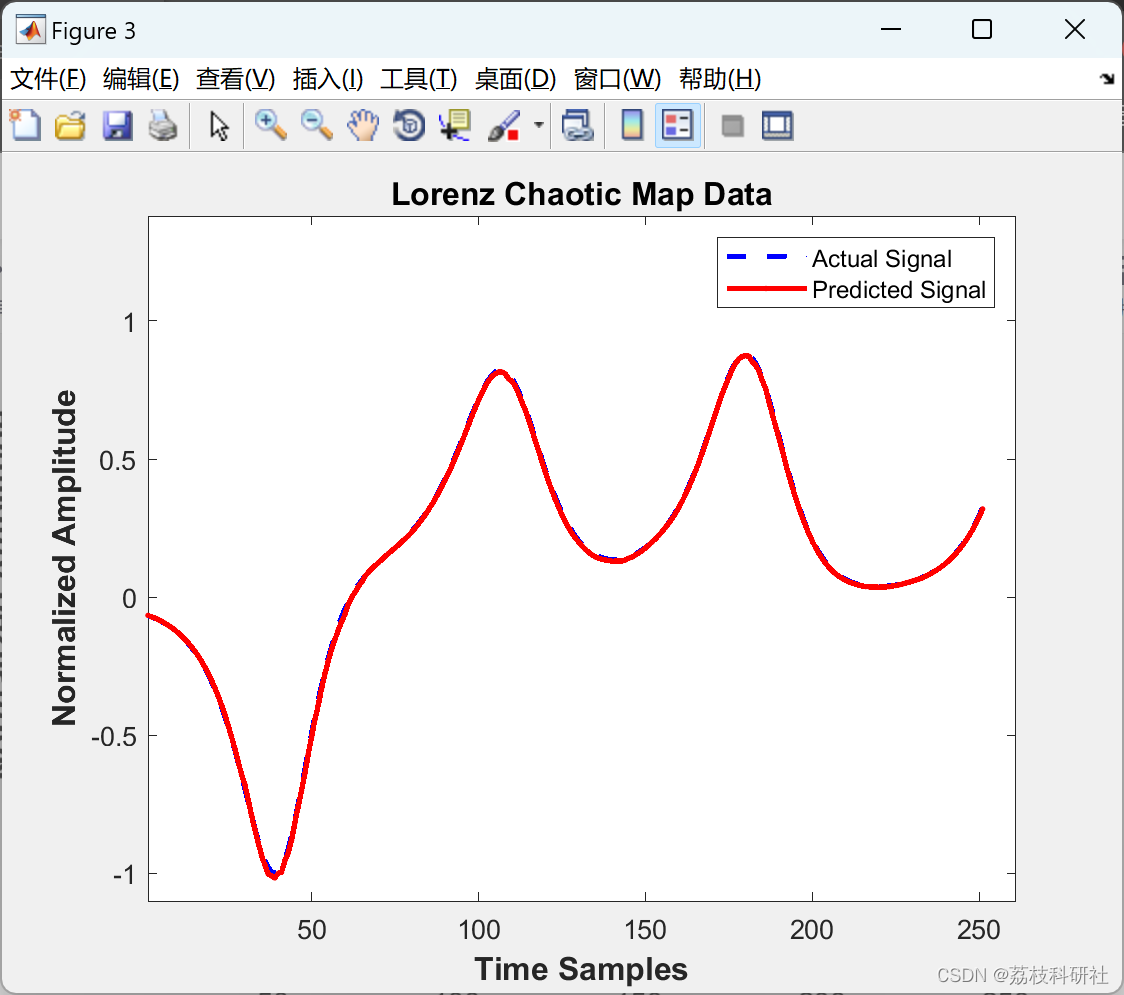
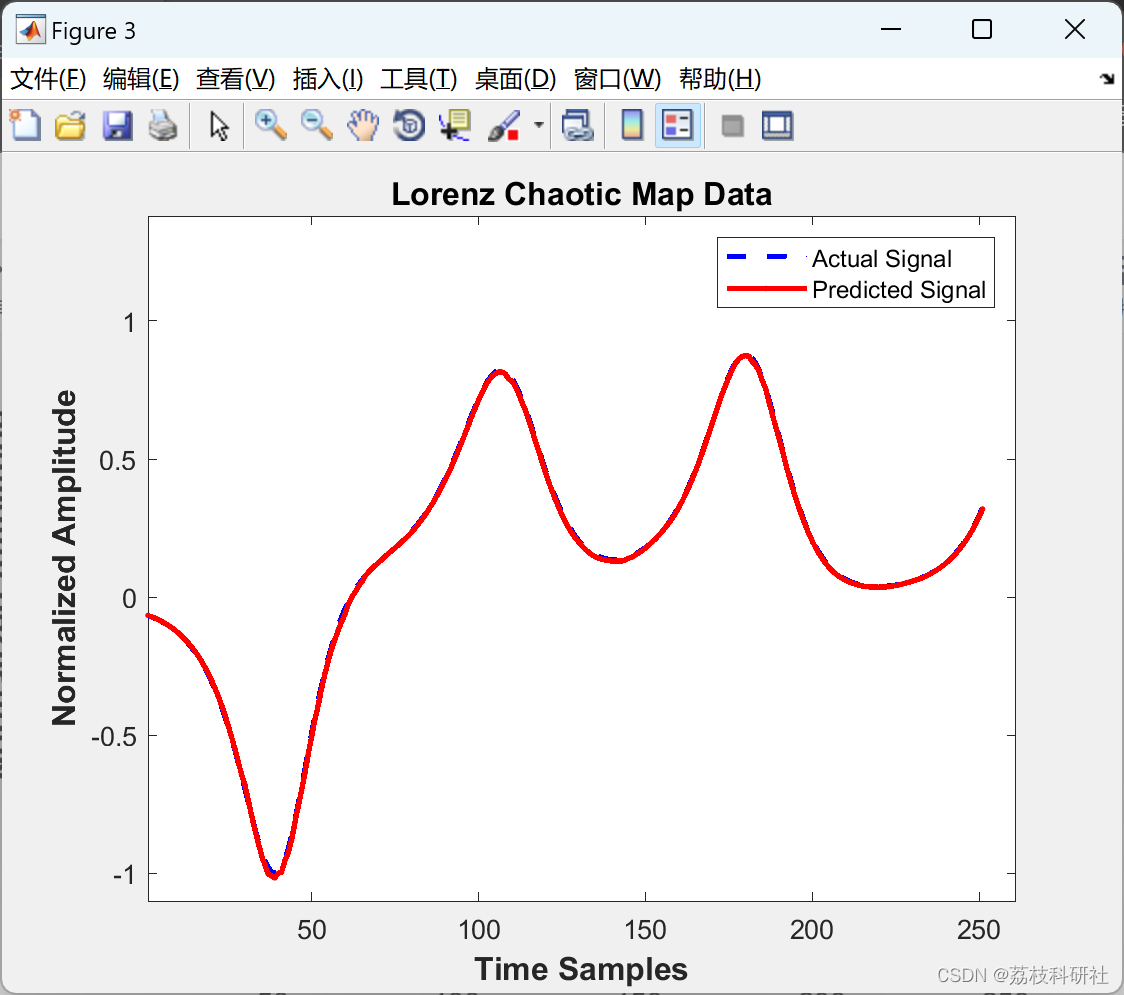
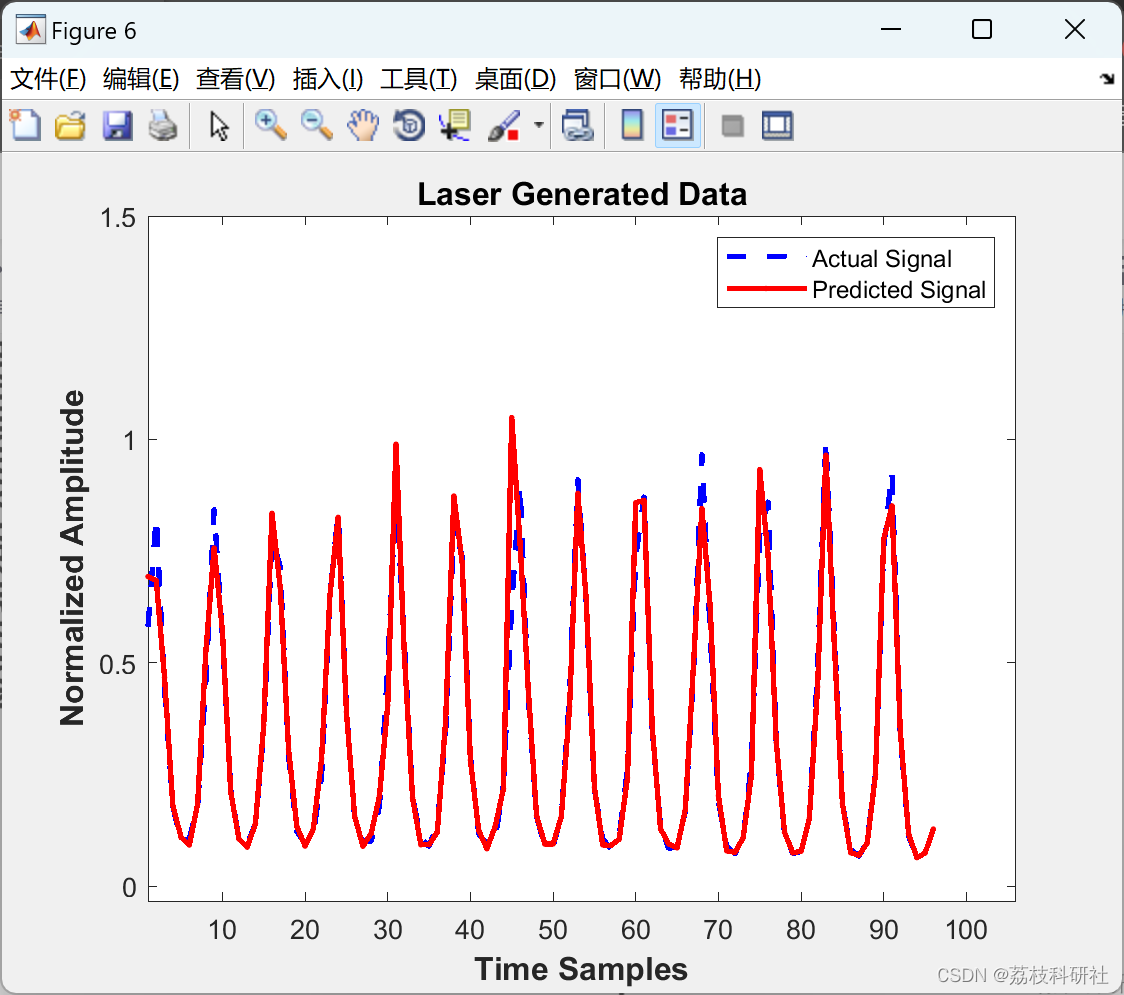
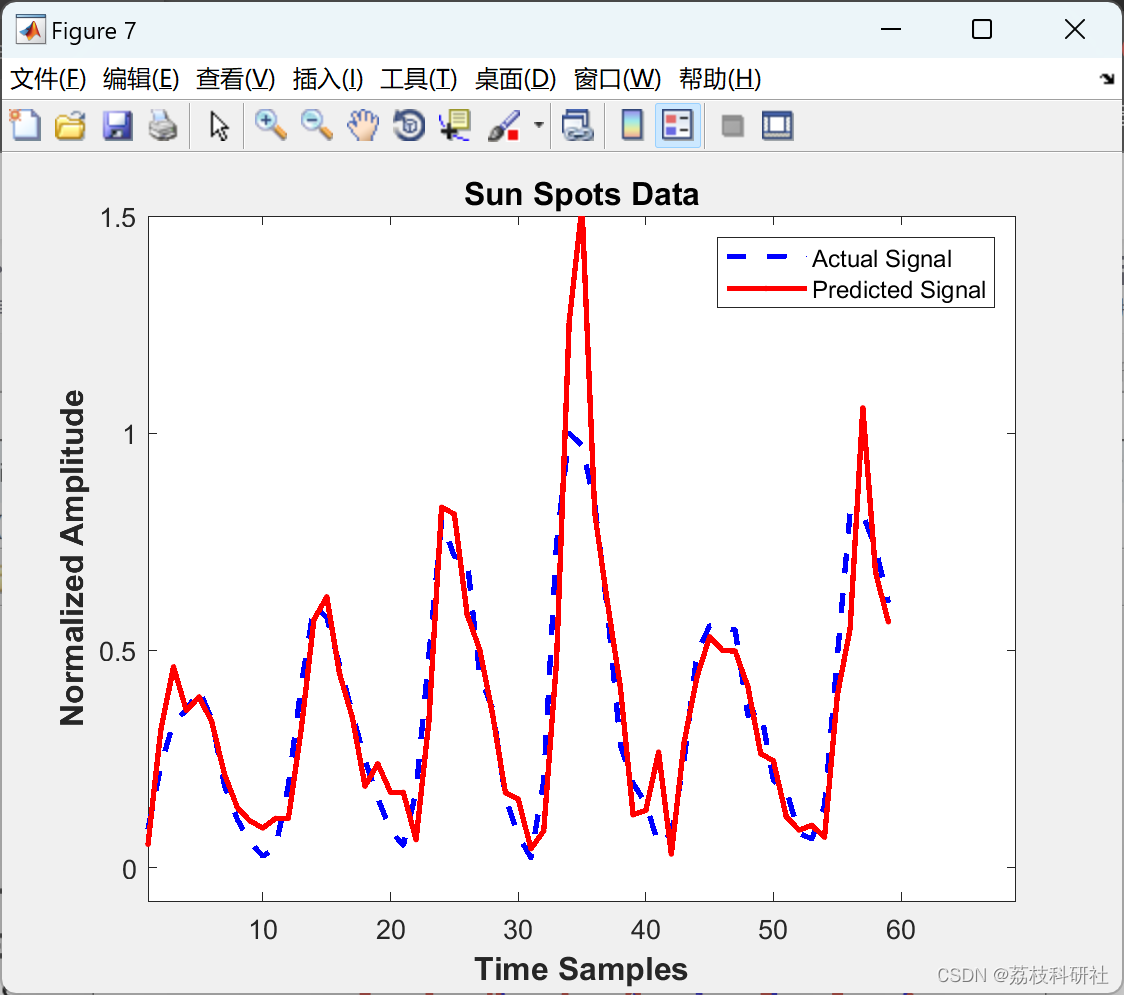
部分代码:
clear all;
%Time series Prediction using Sparse coding with overcomplete dictionaries
%In each case, the test data prediction is plotted versus the real data
%and the sparsity of the solution is recorded.
%both L1-magic (if LASSO=0) and CVX libraries (if LASSO=1) must be included
% in the Matlab path
%if normalize=1 use sqrt(x*x'), normalize=2 use st.dev., normalize=3 use
%the L1 norm, or zero then no normalization.
normalize1=2;
normalize2=2;
eps=0.001; %the error constraint
thr=0.001; %the pruning threshold
NN=20000; %these are the max number of neighbors allowed
dthr=0.0; %the distance threshold used to filter the dictionary. If it
%is zero then no dictionary filtering is done
LASSO=1; %0 for BP and 1 for BPDN or LASSO using CVX
for kkk=1:16 %The 16 data sets used for evaluation
nnnn=kkk;
if(nnnn==1) %Mackey-Glass data
load MGData;
a = MGData;
time = a(:, 1);
x_t = a(:, 2);
trn_data = zeros(500, 5);
chk_data = zeros(500, 5);
time = 1:sz;
Train = x_t(1:100);
Test = x_t(101:190);
K=6;
eps=0.001;
C = 'USD-EURO Data'
elseif(nnnn==15)
load IkedaData1; %Z-normalized
if(nonorm==1)
for i=1:L1-K
dzz(i)=1;
end
end
end
%Now we normalize the targets of the training data
for i=1:L1-K
if(normalize1==5)
T(i) = (trg1(i)-dmm(i))/dvv(i);
else
T(i) = trg1(i)/dzz(i);
end
end
TR = T;
%%%%%%%%This is the dictionary filtering process (if we want to reduce the
%%%%%%%%number of similar atoms. It is controlled by the dthr value
%%%%%%%%specified by the user. I have not investigated this a lot
dictsize=size(DD);
nn=dictsize(1); %the large dimension
mm=dictsize(2); %the small dimension
RR=randn(nn,mm);
RR=orth(RR);
tooclose=0;
for io=1:nn %over all the atoms
xio = DD(io,1:mm);
cnt=0;
for jo= io+1 : nn
dddd(jo) = dist(xio,DD(jo,1:mm)');
if(dddd(jo) <= dthr) cnt=cnt+1; %one or more atoms are too close
end
end
if(io<nn)
mindist(io) = min(dist(xio,DD(io+1:nn,1:mm)')); %the min distance for each atom with the next ones
else
mindist(io)=0;
end
if(cnt==0) %no atoms are too close
FF(io,1:mm) = DD(io,1:mm);
FT(io) = TR(io);
else %some atoms are too close, so we remove this one and put a random atom
FF(io,1:mm) = RR(io, 1:mm);
FT(io) = 0; %the target for the random atoms is zero
tooclose=tooclose+1;
end
end
%So, now the new dictionary is FF and the new targets is FT
%(if no filtering happened then FF is the same as DD)
TooClose(kkk) = tooclose; %this will tell us how many atoms were replaced (removed)
MinDist(kkk,1:nn)=mindist(1:nn);
%here we construct the test data
Test(1:(L2-K),1:K) = tst(1:(L2-K),1:K);
TT = trg2(1:(L2-K));
M=L2-K;
tic %to get the test time
sprs=0; %to accumulate the sparsity over test vectors
for i=1:M %loop over M vectors from the test data
disp('**************');
disp(i);
test(1:K) = Test(i,1:K);
%here we normalize the test vector by its own dot product
if(normalize2==1) normtest = sqrt(test*test');
elseif(normalize2==2) normtest = sqrt(var(test));
elseif(normalize2==3) normtest = norm(test,1);
elseif(normalize2==0) normtest=1;
end
🎉3 参考文献
部分理论来源于网络,如有侵权请联系删除。
[1]Waleed Fakhr, "Sparse Locally Linear and Neighbor Embedding for Nonlinear Time Series Prediction", ICCES 2015, December 2015.
🌈4 Matlab代码实现
相关文章:

用于非线性时间序列预测的稀疏局部线性和邻域嵌入(Matlab代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...

使用 Vue3 重构 Vue2 项目
目录前言:一、项目整体效果展示二、项目下载使用方法三、为什么要重构项目四、重构的流程五、步骤中的 bug 以及解决方式六、未解决的问题总结:前言: 2020年9月18日,vue3正式版发布了,前几天学习完成后,我决…...
Hive学习——单机版Hive的安装
目录 一、基本概念 (一)什么是Hive (二)优势和特点 (三)Hive元数据管理 二、Hive环境搭建 1.自动安装脚本 2./opt/soft/hive312/conf目录下创建hive配置文件hive-site.xml 3.拷贝一个jar包到hive下面的lib目录下 4.删除hive的guava,拷贝hadoop下的guava 5…...
uprobe 实战
观测数据源 目前按照我的理解,和trace相关的常用数据源–探针 大致分为四类。 内核 Trace point kprobe 用户程序 USDT uprobe 在用户程序中,USDT是所谓的静态Tracepoint。和内核代码中的Trace point类似。实现方式是在代码开发时,使用USDT…...
| 真题+思路+考点+代码+岗位)
华为OD机试 - 求最大数字(Python)| 真题+思路+考点+代码+岗位
求最大数字 题目 给定一个由纯数字组成以字符串表示的数值,现要求字符串中的每个数字最多只能出现2次,超过的需要进行删除;删除某个重复的数字后,其它数字相对位置保持不变。 如34533,数字3重复超过2次,需要删除其中一个3,删除第一个3后获得最大数值4533 请返回经过删…...

雨水情测报与大坝安全监测系统
压电式雨量传感器产品概述传感器由上盖、外壳和下盖组成,壳体内部有压电片和电路板,可以固定在外径50mm立柱上和气象站横杆上。传感器采用冲击测量原理对单个雨滴重量进行测算,进而计算降雨量。雨滴在降落过程中受到雨滴重量和空气阻力的作用…...

抖音广告投放形式有哪些?新品牌进入抖音怎么建立口碑
坐拥5亿用户的抖音平台,已经成为各大品牌的兵家必争之地。想要在这块宣传的“高地”,做出声量,就必须了解抖音广告投放形式有哪些。这里整理的这份抖音广告投放指南,你一定不能错过。一、抖音为何如此牛想要弄清楚抖音广告的投放形…...

Beefxss使用教程图文教程(超详细)
「作者主页」:士别三日wyx 「作者简介」:CSDN top100、阿里云博客专家、华为云享专家、网络安全领域优质创作者 Beefxss一、首次使用二、修改账号密码三、自带练习页面四、简单使用五、工具界面介绍六、功能演示1、网页重定向2、社工弹窗3、功能颜色标识…...
)
【Python学习笔记】35.Python3 CGI编程(2)
前言 本章继续介绍Python的CGI编程。 通过CGI程序传递checkbox数据 checkbox用于提交一个或者多个选项数据,HTML代码如下: 实例 <!DOCTYPE html> <html> <head> <meta charset"utf-8"> <title>csdn教程(csd…...

博客等级说明
CSDN 博客等级是按照用户的博客积分数量进行的设定,为 Lv1 至 Lv10 共 10 个等级,不同的等级创作者可以享受到不同的权益待遇。例如,皮肤奖励、自定义域名、客服优先处理、自定义文章标签等特权。您需要提高博客积分进一步提升等级࿰…...
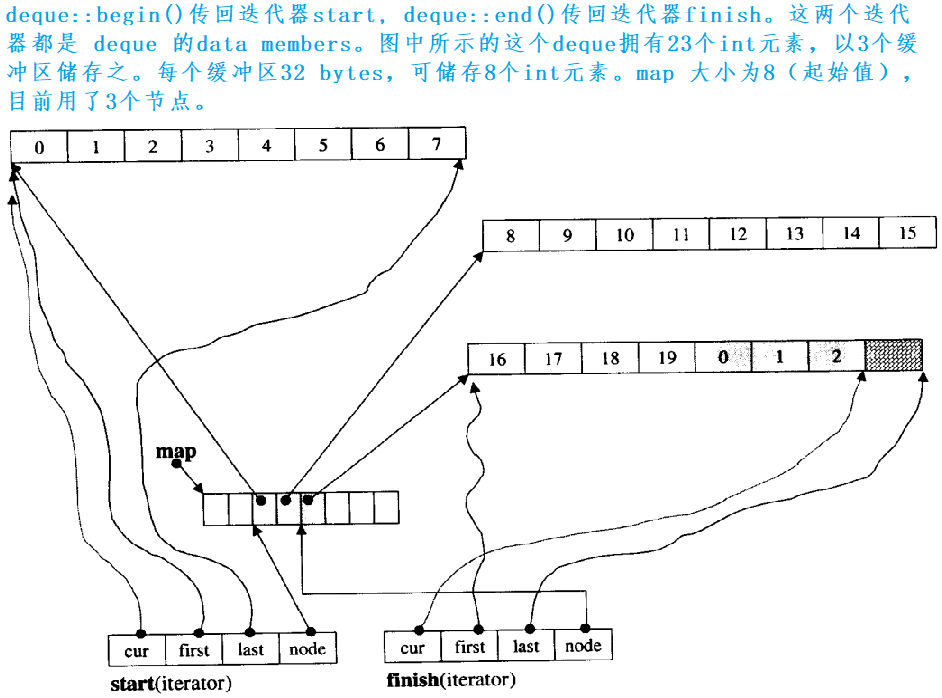
STL——容器适配器、deque
一、容器适配器 1.适配器 适配器是一种设计模式(设计模式是一套被反复使用的、多数人所知晓的、经过分类编目的、代码设计经验的总结),该种模式是将一个类的接口转换成客户希望的另外一个接口。 2.STL标准库中stack和queue的底层结构 stack…...

VBA数组和Excel工作表数据传递
本文介绍如何利用 VBA 的数组(Array) 来提高 Excel 单元格和外部数据传输的性能。如果数量比较大,通过 Array 来传输数据比直接操作单元格要快若干倍。 将 Range 的数据写入 VBA Array 将 Range 数据写入 VBA 的数组非常简单。下面的例子演示了用法&am…...
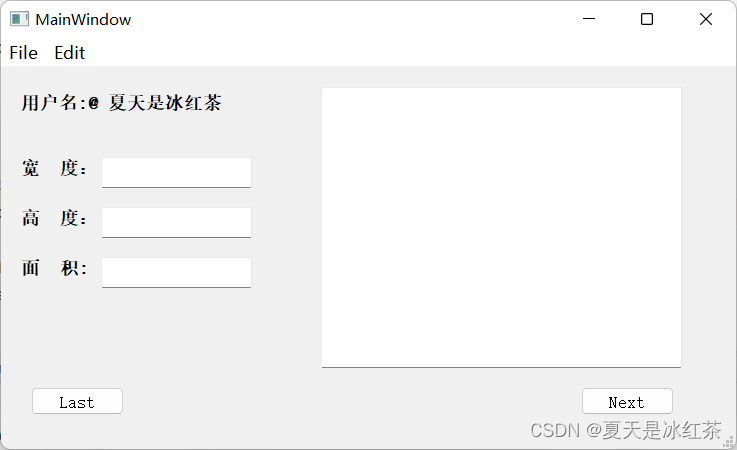
PyQt5保姆级入门教程——从安装到使用
目录 Part1:安装PyQt5 Part 2:PyCharm配置PyQt5 Part 3:PyQt5设计界面介绍 Part 4:PyQt5设计UI 今天看了多个大佬的教程,总算是把PyQt5开发弄好了,每个部分都要看几个人的十分不方便,我十分…...
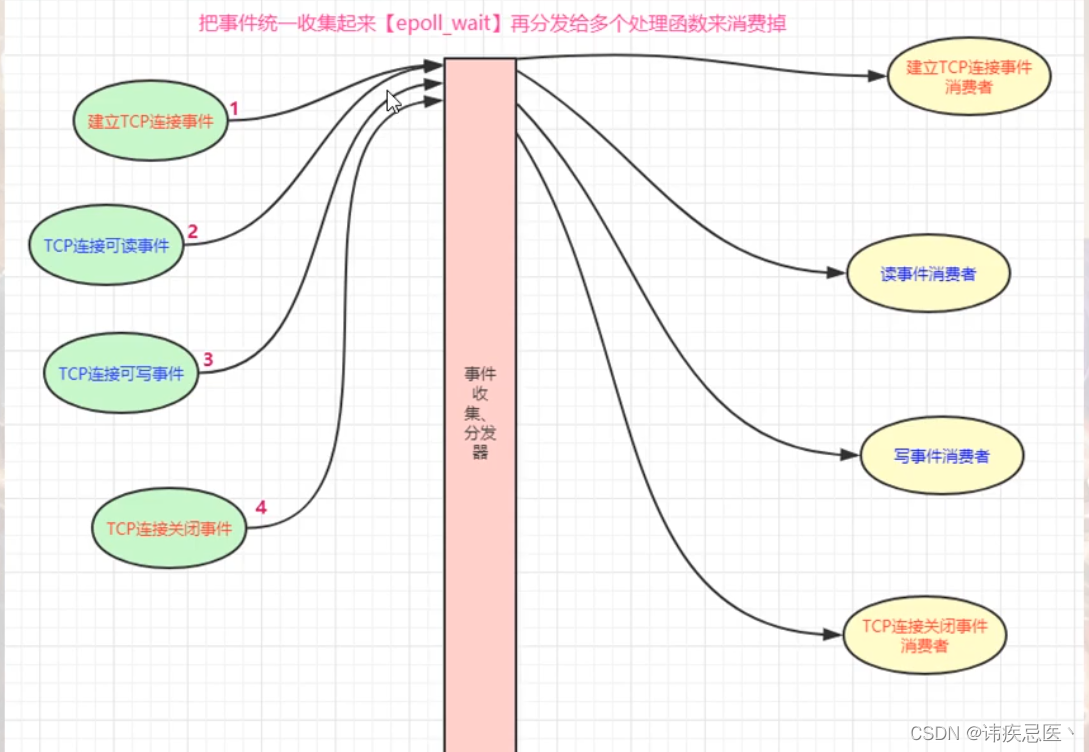
1.6 epoll实战使用
文章目录1、连接池2、epoll两种工作模式2.1、LT模式2.2、ET模式3、后端开发面试题4、epoll验证1、连接池 将每一个套接字和一块内存进行绑定,连接池就是一个结构体数组,通过链表来维护一个空闲连接。 1、ngx_get_connection(int fd)从空闲链表取一个空闲…...

JDK定时、Spring定时、时间轮定时小结
Timer使用一个线程,一个小根堆。线程执行根上的任务,小根堆会根据执行时间戳重新调整,根上的任务是下一个执行的任务。 DelayedQueue维护一个优先级队列,本质也是一个数组方式的堆。任务生成时也有时间戳,只提供存储。…...
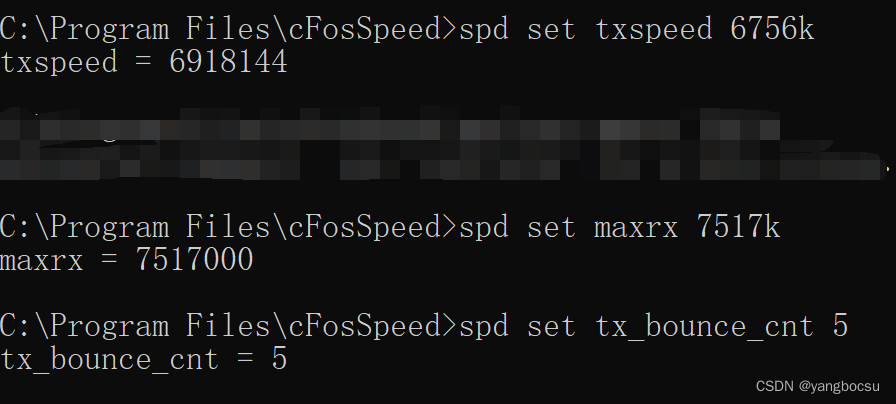
关于cFosSpeed如何配置
cFosSpeed配置一、检查Calibration Done情况二、优化Ping时间和线路校准三、测网速四、cFosSpeed控制台五、配置参数一、检查Calibration Done情况 安装完毕,激活成功后。 右键------>选项------>设置, 打开适配器信息,查看Calibra…...
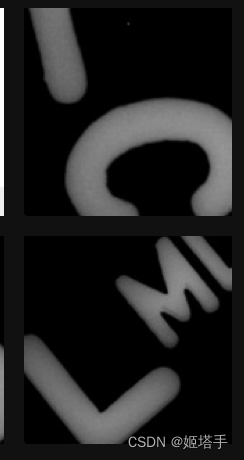
YOLOV5输出的txt里面有什么猫腻(用于图像分类竞赛中提升图像信息密度)
背景概括: kaggle最近举办了一场医学乳腺癌检测的比赛(图像分类) 比赛官网地址 给的数据是dcm的专业的医学格式,自己通过DICOM库转为png后,发现该图像胸部不同的患者乳腺大小不一,简言之乳腺的CT有效图在…...

vue+axios常用操作
vueaxios常用操作vue2axios请求拦截依赖项http.jsvue2axios设置请求头依赖项http.js获取并设置请求头api.jsa.vuevue2axios请求拦截 依赖项 “vue”: “^2.6.11” “axios”: “^0.21.0” “element-ui”: “^2.13.2”(做弹窗提示,可以不用) http.js // 引入axi…...
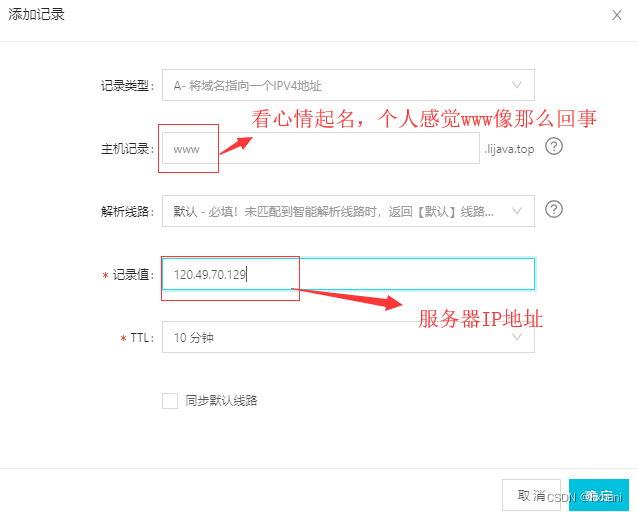
Xshell连接阿里云服务器搭建网站
一、建设一个网站的基本要求 申请一个独立的域名申请一台云服务器ECS在服务器上安装网站环境,如:Apache发布网站内容至云服务器将第一步注册的域解析至云服务器的外网IP地址进行ICP备案 二、用户访问网站的过程 在浏览器上输入域名浏览器自动调用DNS&…...
嵌入式ARM设计编程(三) 处理器工作模式
文章和代码已归档至【Github仓库:hardware-tutorial】,需要的朋友们自取。或者公众号【AIShareLab】回复 嵌入式 也可获取。 一、实验目的 (1) 通过实验掌握学会使用msr/mrs 指令实现ARM 处理器工作模式的切换,观察不…...

(LeetCode 每日一题) 3442. 奇偶频次间的最大差值 I (哈希、字符串)
题目:3442. 奇偶频次间的最大差值 I 思路 :哈希,时间复杂度0(n)。 用哈希表来记录每个字符串中字符的分布情况,哈希表这里用数组即可实现。 C版本: class Solution { public:int maxDifference(string s) {int a[26]…...

谷歌浏览器插件
项目中有时候会用到插件 sync-cookie-extension1.0.0:开发环境同步测试 cookie 至 localhost,便于本地请求服务携带 cookie 参考地址:https://juejin.cn/post/7139354571712757767 里面有源码下载下来,加在到扩展即可使用FeHelp…...

黑马Mybatis
Mybatis 表现层:页面展示 业务层:逻辑处理 持久层:持久数据化保存 在这里插入图片描述 Mybatis快速入门 
通过Wrangler CLI在worker中创建数据库和表
官方使用文档:Getting started Cloudflare D1 docs 创建数据库 在命令行中执行完成之后,会在本地和远程创建数据库: npx wranglerlatest d1 create prod-d1-tutorial 在cf中就可以看到数据库: 现在,您的Cloudfla…...

iPhone密码忘记了办?iPhoneUnlocker,iPhone解锁工具Aiseesoft iPhone Unlocker 高级注册版分享
平时用 iPhone 的时候,难免会碰到解锁的麻烦事。比如密码忘了、人脸识别 / 指纹识别突然不灵,或者买了二手 iPhone 却被原来的 iCloud 账号锁住,这时候就需要靠谱的解锁工具来帮忙了。Aiseesoft iPhone Unlocker 就是专门解决这些问题的软件&…...

前端导出带有合并单元格的列表
// 导出async function exportExcel(fileName "共识调整.xlsx") {// 所有数据const exportData await getAllMainData();// 表头内容let fitstTitleList [];const secondTitleList [];allColumns.value.forEach(column > {if (!column.children) {fitstTitleL…...

Auto-Coder使用GPT-4o完成:在用TabPFN这个模型构建一个预测未来3天涨跌的分类任务
通过akshare库,获取股票数据,并生成TabPFN这个模型 可以识别、处理的格式,写一个完整的预处理示例,并构建一个预测未来 3 天股价涨跌的分类任务 用TabPFN这个模型构建一个预测未来 3 天股价涨跌的分类任务,进行预测并输…...

大语言模型如何处理长文本?常用文本分割技术详解
为什么需要文本分割? 引言:为什么需要文本分割?一、基础文本分割方法1. 按段落分割(Paragraph Splitting)2. 按句子分割(Sentence Splitting)二、高级文本分割策略3. 重叠分割(Sliding Window)4. 递归分割(Recursive Splitting)三、生产级工具推荐5. 使用LangChain的…...
)
WEB3全栈开发——面试专业技能点P2智能合约开发(Solidity)
一、Solidity合约开发 下面是 Solidity 合约开发 的概念、代码示例及讲解,适合用作学习或写简历项目背景说明。 🧠 一、概念简介:Solidity 合约开发 Solidity 是一种专门为 以太坊(Ethereum)平台编写智能合约的高级编…...

省略号和可变参数模板
本文主要介绍如何展开可变参数的参数包 1.C语言的va_list展开可变参数 #include <iostream> #include <cstdarg>void printNumbers(int count, ...) {// 声明va_list类型的变量va_list args;// 使用va_start将可变参数写入变量argsva_start(args, count);for (in…...

