动态规划——股票问题全解
引入
股票问题是一类动态问题,我们需要对其状态进行判定分析来得出答案
但其实,我们只需要抓住两个点,持有和不持有,在这两种状态下分析问题会简单清晰许多
下面将会对各个问题进行分析讲解,来解释什么是持有和不持有状态,并在分析后得到题目的解答买卖股票的最佳时机
1、买卖股票的最佳时机
给定一个数组 prices ,它的第 i 个元素 prices[i] 表示一支给定股票第 i 天的价格。
你只能选择 某一天 买入这只股票,并选择在 未来的某一个不同的日子 卖出该股票。设计一个算法来计算你所能获取的最大利润。
返回你可以从这笔交易中获取的最大利润。如果你不能获取任何利润,返回 0 。
示例 1:
输入:[7,1,5,3,6,4]
输出:5
解释:在第 2 天(股票价格 = 1)的时候买入,在第 5 天(股票价格 = 6)的时候卖出,最大利润 = 6-1 = 5 。注意利润不能是 7-1 = 6, 因为卖出价格需要大于买入价格;同时,你不能在买入前卖出股票。
示例 2:
输入:prices = [7,6,4,3,1]
输出:0
解释:在这种情况下, 没有交易完成, 所以最大利润为 0。
分析:
我们了解到这道题,只能够购买和卖出一次,那么,
持有的状态只有两种情况:1.之前就持有 2.今天刚买入
不持有也有两种情况:1.昨天就不持有 2.今天刚出售
1.dp空间
通过以上的分析我们可以知道,解决这个问题我们需要了解:
1.今天的价格 2.昨天的状态
所以,我们需要两对空间,保存两对持有与不持有状态
即一个2*2大小的数组
vector<vector<int>> dp(2, vector<int>(2));2.初始状态
其中dp[i][0] 代表第i天的持有状态下的资金数
dp[i][1] 代表第i天的不持有状态下的资金数
由此我们也可以知道,第一天的持有状态只能是进行买入 即 -prices[0]
不持有状态只能是0
所以初始状态我们也有了
dp[0][0] = -prices[0];
dp[0][1] = 0;3.递推公式
由刚开始的分析其实我们已经知道了递推公式,现在只需要进行代码实现即可:
先使用伪代码描述
当天持有股票的最大金额 = max(昨天就持有时的资金数,今天刚买入后所拥有的资金)
当天不持有股票的最大金额 = max(昨天就不持有时的资金数,今天刚卖出后所拥有的资金)
代码实现
其中的取模运算是为了获得之前的状态而不用进行数据移动
//因为只进行一次买入卖出,所以当前买入一定是 0 - prices[i]
dp[i % 2][0] = max(dp[(i - 1) % 2][0], -prices[i]);
dp[i % 2][1] = max(dp[(i - 1) % 2][1], prices[i] + dp[(i - 1) % 2][0]);4.题解代码
class Solution {
public:int maxProfit(vector<int>& prices) {int len = prices.size();vector<vector<int>> dp(2, vector<int>(2)); dp[0][0] = -prices[0];dp[0][1] = 0;for (int i = 1; i < len; i++) {dp[i % 2][0] = max(dp[(i - 1) % 2][0], -prices[i]);dp[i % 2][1] = max(dp[(i - 1) % 2][1], prices[i] + dp[(i - 1) % 2][0]);}return dp[(len - 1) % 2][1];}
};2、买卖股票的最佳时机 II
给定一个数组,它的第 i 个元素是一支给定股票第 i 天的价格。
设计一个算法来计算你所能获取的最大利润。你可以尽可能地完成更多的交易(多次买卖一支股票)。
注意:你不能同时参与多笔交易(你必须在再次购买前出售掉之前的股票)。
示例 1:
输入: [7,1,5,3,6,4]
输出: 7
解释: 在第 2 天(股票价格 = 1)的时候买入,在第 3 天(股票价格 = 5)的时候卖出, 这笔交易所能获得利润 = 5-1 = 4。随后,在第 4 天(股票价格 = 3)的时候买入,在第 5 天(股票价格 = 6)的时候卖出, 这笔交易所能获得利润 = 6-3 = 3 。
示例 2:
输入: [1,2,3,4,5]
输出: 4
解释: 在第 1 天(股票价格 = 1)的时候买入,在第 5 天 (股票价格 = 5)的时候卖出, 这笔交易所能获得利润 = 5-1 = 4 。注意你不能在第 1 天和第 2 天接连购买股票,之后再将它们卖出。因为这样属于同时参与了多笔交易,你必须在再次购买前出售掉之前的股票。
示例 3:
输入: [7,6,4,3,1]
输出: 0
解释: 在这种情况下, 没有交易完成, 所以最大利润为 0。
提示:
- 1 <= prices.length <= 3 * 10 ^ 4
- 0 <= prices[i] <= 10 ^ 4
分析:
这道题与上一道题的最大差别就是,可进行多次买入卖出,那么如上一道题相同,先分析两种状态
持有的状态只有两种情况:1.之前就持有 2.今天买入
不持有也有两种情况:1.昨天就不持有 2.今天出售
1.dp空间
通过以上的分析我们可以知道,解决这个问题我们需要了解:
1.今天的价格 2.昨天的状态
所以,我们需要两对空间,保存两对持有与不持有状态
即一个2*2大小的数组
vector<vector<int>> dp(2, vector<int>(2));2.初始状态
其中dp[i][0] 代表第i天的持有状态下的资金数
dp[i][1] 代表第i天的不持有状态下的资金数
由此我们也可以知道,第一天的持有状态只能是进行买入 即 -prices[0]
不持有状态只能是0
所以初始状态与上一道题相同
dp[0][0] = -prices[0];
dp[0][1] = 0;
3.递推公式
使用伪代码描述
当天持有股票的最大金额 = max(昨天就持有时的资金数,今天买入后所拥有的资金)
当天不持有股票的最大金额 = max(昨天就不持有时的资金数,今天刚卖出后所拥有的资金)
代码实现
其中的取模运算是为了获得之前的状态而不用进行数据移动
注意,因为需要进行多次买入卖出,所以 持有股票状态中 今天买入后所拥有的资金 需要由之前的状态转换而来,这是与前一道题不同的地方
//注意,这里的今天买入状态,是由昨天未持有状态推导而来
dp[i % 2][0] = max(dp[(i - 1) % 2][0], dp[(i - 1) % 2][1] - prices[i]);
dp[i % 2][1] = max(dp[(i - 1) % 2][1], prices[i] + dp[(i - 1) % 2][0]);4.题解代码
class Solution {
public:int maxProfit(vector<int>& prices) {int len = prices.size();vector<vector<int>> dp(2, vector<int>(2));dp[0][0] -= prices[0];dp[0][1] = 0;for (int i = 1; i < len; i++) {dp[i % 2][0] = max(dp[(i - 1) % 2][0], dp[(i - 1) % 2][1] - prices[i]);dp[i % 2][1] = max(dp[(i - 1) % 2][1], prices[i] + dp[(i - 1) % 2][0]);}return dp[(len - 1) % 2][1];}
};3、买卖股票的最佳时机 III
给定一个数组,它的第 i 个元素是一支给定的股票在第 i 天的价格。
设计一个算法来计算你所能获取的最大利润。你最多可以完成 两笔 交易。
注意:你不能同时参与多笔交易(你必须在再次购买前出售掉之前的股票)。
示例 1: 输入:prices = [3,3,5,0,0,3,1,4] 输出:6 解释:在第 4 天(股票价格 = 0)的时候买入,在第 6 天(股票价格 = 3)的时候卖出,这笔交易所能获得利润 = 3-0 = 3 。随后,在第 7 天(股票价格 = 1)的时候买入,在第 8 天 (股票价格 = 4)的时候卖出,这笔交易所能获得利润 = 4-1 = 3。
示例 2: 输入:prices = [1,2,3,4,5] 输出:4 解释:在第 1 天(股票价格 = 1)的时候买入,在第 5 天 (股票价格 = 5)的时候卖出, 这笔交易所能获得利润 = 5-1 = 4。注意你不能在第 1 天和第 2 天接连购买股票,之后再将它们卖出。因为这样属于同时参与了多笔交易,你必须在再次购买前出售掉之前的股票。
示例 3: 输入:prices = [7,6,4,3,1] 输出:0 解释:在这个情况下, 没有交易完成, 所以最大利润为0。
示例 4: 输入:prices = [1] 输出:0
提示:
- 1 <= prices.length <= 10^5
- 0 <= prices[i] <= 10^5
分析:
这道题与前题的差别在于,只能进行两笔交易,即两次买入卖出过程,那么如上一道题相同,先分析两笔交易各自的状态
第一笔:
持有的状态只有两种情况:1.之前就持有 2.今天刚买入
不持有也有两种情况:1.昨天就不持有 2.今天刚出售
但是情况不同的是,第二笔的交易,需要根据第一笔交易的基础上进行
所以第二笔:
持有的状态只有两种情况:1.之前就持有 2.今天刚买入(但需要加上前一笔交易完成的状态)
不持有也有两种情况:1.昨天就不持有 2.今天刚出售
1.dp空间
通过以上的分析我们可以知道,解决这个问题我们需要了解:
1.第一笔交易的持有与不持有状态 2.第一笔交易的持有与不持有状态
所以,我们需要两对空间,保存两笔交易的状态
即一个2*2大小的数组
vector<vector<int>> dp(2, vector<int>(2, 0));
2.初始状态
其中dp[i][0] 代表第i天的持有状态下的资金数
dp[i][1] 代表第i天的不持有状态下的资金数
由此我们也可以知道,第一天第一笔的持有状态只能是进行买入 即 -prices[0]
不持有状态只能是0
又因为第二笔的状态根据第一笔的状态转换
所以第二笔的持有状态是第一笔的不持有状态-当前价格 即 0-prices[0]
不持有状态只能是0
所以初始状态如下
dp[0][0] = -prices[0];
dp[1][0] = -prices[0];
3.递推公式
使用伪代码描述
第一笔交易持有股票的最大金额 = max(昨天就持有时的资金数,今天买入后所拥有的资金)
第一笔交易不持有股票的最大金额 = max(昨天就不持有时的资金数,今天刚卖出后所拥有的资金)
第二笔交易持有股票的最大金额 = max(昨天就持有时的资金数,今天买入后所拥有的资金)
第二笔交易不持有股票的最大金额 = max(昨天就不持有时的资金数,今天刚卖出后所拥有的资金)
代码实现
至于为什么不保存第一笔之前的状态了,大致可以理解为,两天合起来才是需要的完整的交易,即第一笔就保存了第二笔之前的数据,第一笔直接交易即可
dp[0][0] = std::max(dp[0][0], 0 - prices[i]);
dp[0][1] = std::max(dp[0][1], prices[i] + dp[0][0]);
dp[1][0] = std::max(dp[1][0], dp[0][1] - prices[i]);
dp[1][1] = std::max(dp[1][1], prices[i] + dp[1][0]);4.题解代码
class Solution {
public:int maxProfit(vector<int>& prices) {int n = prices.size();vector<vector<int>> dp(2, vector<int>(2, 0));dp[0][0] = -prices[0];dp[1][0] = -prices[0];for (int i = 1; i < n; ++i) {dp[0][0] = std::max(dp[0][0], 0 - prices[i]);dp[0][1] = std::max(dp[0][1], prices[i] + dp[0][0]);dp[1][0] = std::max(dp[1][0], dp[0][1] - prices[i]);dp[1][1] = std::max(dp[1][1], prices[i] + dp[1][0]);}return dp[1][1];}
};4、买卖股票的最佳时机 IV
给定一个整数数组 prices ,它的第 i 个元素 prices[i] 是一支给定的股票在第 i 天的价格。
设计一个算法来计算你所能获取的最大利润。你最多可以完成 k 笔交易。
注意:你不能同时参与多笔交易(你必须在再次购买前出售掉之前的股票)。
示例 1: 输入:k = 2, prices = [2,4,1] 输出:2 解释:在第 1 天 (股票价格 = 2) 的时候买入,在第 2 天 (股票价格 = 4) 的时候卖出,这笔交易所能获得利润 = 4-2 = 2。
示例 2: 输入:k = 2, prices = [3,2,6,5,0,3] 输出:7 解释:在第 2 天 (股票价格 = 2) 的时候买入,在第 3 天 (股票价格 = 6) 的时候卖出, 这笔交易所能获得利润 = 6-2 = 4。随后,在第 5 天 (股票价格 = 0) 的时候买入,在第 6 天 (股票价格 = 3) 的时候卖出, 这笔交易所能获得利润 = 3-0 = 3 。
提示:
- 0 <= k <= 100
- 0 <= prices.length <= 1000
- 0 <= prices[i] <= 1000
分析:
其实这道题与前一道题是相同的题目,只是将交易次数修改为任意次数
只需要与上道题进行相同的模式即可
这里就直接摆出代码:
但需要注意的是,第一笔交易买入时肯定是0 - prices[i]的价值,所以在此处使用多开一层数组,来保持动态的首次为0的概念,即代码中的
dp[j - 1][1] - prices[i]
class Solution {
public:int maxProfit(int k, vector<int>& prices) {int n = prices.size();vector<vector<int>> dp(k + 1, vector<int>(2, 0));for (int i = 1; i <= k; ++i) {dp[i][0] = -prices[0];}for (int i = 1; i < n; ++i) {for (int j = 1; j <= k; ++j) {dp[j][0] = std::max(dp[j][0], dp[j - 1][1] - prices[i]);dp[j][1] = std::max(dp[j][1], prices[i] + dp[j][0]);}}return dp[k][1];}
};5、最佳买卖股票时机含冷冻期
给定一个整数数组,其中第 i 个元素代表了第 i 天的股票价格 。
设计一个算法计算出最大利润。在满足以下约束条件下,你可以尽可能地完成更多的交易(多次买卖一支股票):
- 你不能同时参与多笔交易(你必须在再次购买前出售掉之前的股票)。
- 卖出股票后,你无法在第二天买入股票 (即冷冻期为 1 天)。
示例:
- 输入: [1,2,3,0,2]
- 输出: 3
- 解释: 对应的交易状态为: [买入, 卖出, 冷冻期, 买入, 卖出]
分析:
这道题与前面的题就不一样了,因为这道题多出了一种状态,即冰冻期的状态
让我们对三种状态进行分析
持有:1.前一天就持有 2.今天刚持有
不持有:1.前一天就不持有 2.今天是冷冻期
冷冻期:今天卖出,进入冷冻期
可能对这个分割会有疑虑,为什么冷冻期的状态不算冷冻期当天,而是算其交易完成的那天
因为我们一直都有在进行转换的判断:
比如:持有的状态,是今天由不持有转向持有
不持有的状态,是由持有转向不持有
所以冷冻期的概念:是由非冷冻期转向冷冻期
2.初始状态
初始状态不涉及冷冻期,所以初始状态没有变化
3.递推公式
使用伪代码描述
交易持有股票的最大金额 = max(昨天就持有时的资金数,今天买入后所拥有的资金)
交易不持有股票的最大金额 = max(昨天就不持有时的资金数,今天是冷冻期的资金)
冷冻期的最大金额 = 今天卖出后的资金
代码实现
dp[i][0] = std::max(dp[i - 1][0], dp[i - 1][1] - prices[i]);
dp[i][1] = std::max(dp[i - 1][2], dp[i - 1][1]);
dp[i][2] = dp[i - 1][0] + prices[i];4.题解代码
注意:交易结束的最大金额,是由两个方面来决定:不持有状态和冷冻期状态
class Solution {
public:int maxProfit(vector<int>& prices) {int n = prices.size();vector<vector<int>> dp(n, vector<int>(3, 0));dp[0][0] = -prices[0];for (int i = 1; i < n; ++i) {dp[i][0] = std::max(dp[i - 1][0], dp[i - 1][1] - prices[i]);dp[i][1] = std::max(dp[i - 1][2], dp[i - 1][1]);dp[i][2] = dp[i - 1][0] + prices[i];}return std::max(dp[n - 1][1], dp[n - 1][2]);}
};6、买卖股票的最佳时机含手续费
给定一个整数数组 prices,其中第 i 个元素代表了第 i 天的股票价格 ;非负整数 fee 代表了交易股票的手续费用。
你可以无限次地完成交易,但是你每笔交易都需要付手续费。如果你已经购买了一个股票,在卖出它之前你就不能再继续购买股票了。
返回获得利润的最大值。
注意:这里的一笔交易指买入持有并卖出股票的整个过程,每笔交易你只需要为支付一次手续费。
示例 1: 输入: prices = [1, 3, 2, 8, 4, 9], fee = 2 输出: 8
解释: 能够达到的最大利润: 在此处买入 prices[0] = 1 在此处卖出 prices[3] = 8 在此处买入 prices[4] = 4 在此处卖出 prices[5] = 9 总利润: ((8 - 1) - 2) + ((9 - 4) - 2) = 8.
注意:
- 0 < prices.length <= 50000.
- 0 < prices[i] < 50000.
- 0 <= fee < 50000.
分析:
这个题就很简单了,只是在第二题的基础上加了个交易费而已
就直接放出代码即可:
此处数组的层数改为n,但依旧是之前保存前一天的概念,没有区别
class Solution {
public:int maxProfit(vector<int>& prices, int fee) {int n = prices.size();vector<vector<int>> dp(n, vector<int>(2, 0));dp[0][0] = -prices[0];for (int i = 1; i < n; ++i) {dp[i][1] = std::max(dp[i - 1][1], dp[i - 1][0] + prices[i] - fee);dp[i][0] = std::max(dp[i - 1][0], dp[i - 1][1] - prices[i]);}return dp[n - 1][1];}
};相关文章:

动态规划——股票问题全解
引入 股票问题是一类动态问题,我们需要对其状态进行判定分析来得出答案 但其实,我们只需要抓住两个点,持有和不持有,在这两种状态下分析问题会简单清晰许多 下面将会对各个问题进行分析讲解,来解释什么是持有和不持…...

想做游戏开发要深入c/c++还是c#?
根据题主描述提三点建议: 先选择一个语言、选择一个引擎能入行确保精通一个及已入行的情况下,技多不压身不必想日后的”退而求其次“,现在的事情还没有开始做就想以后,太过虚无及功利了 下面是这三点的详细说明: 【选…...

【JMeter】【Mac】如何在Mac上打开JMeter
平常我们在Windows电脑里打开JMeter,只要双击JMeter.bat即可打开,那我换了Mac后,该怎么打开JMeter呢 一、命令行打开JMeter 1、打开JMeter路径 cd /Users/work/apache-jmeter-5.2/bin 2、运行JMeter sh jmeter 3、如果涉及到一些权限无…...
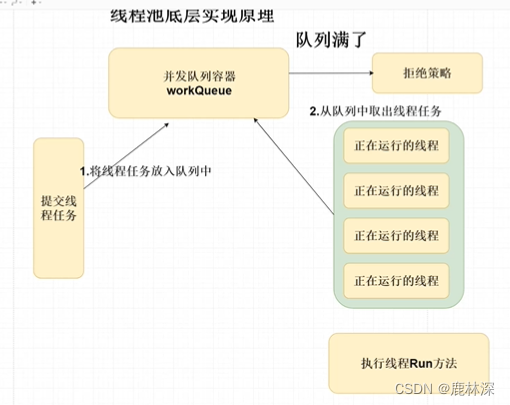
JAVA面试八股文一(并发与线程)
并发的三大特性原子性:cpu在执行过程不可以暂停然后再调度,不可以中断,要不全部执行完,要不全部不执行。可见性:当多个线程访问同一个变量时,一个线程改变了这个变量的值,其他线程能够立即看到修…...

C语言二级指针
目录一、1. 指针的作用2.二级指针3. 为什么要用二级指针一、 1. 指针的作用 内存的存储区就像一池湖水,数据就像池水里面的鱼,如果不用内存寻址的方式,那么当你找某个特定数据的时候,就相当于在一池湖水里找某一条叫做“张三”的…...

[java-面试]初级、中级、高级具备的技术栈和知识点
🌟1.java初级1. Java基础知识:语法、包装类、泛型、数据结构和继承,以及基础API。2. Java开发工具:如Eclipse,NetBeans,Maven等。3. Java Web开发技术:如Servlet,JSP,Str…...

「5」线性代数(期末复习)
🚀🚀🚀大家觉不错的话,就恳求大家点点关注,点点小爱心,指点指点🚀🚀🚀 目录 第四章 向量组的线性相关性 &5)向量空间 第五章 相似矩阵及二次型 &a…...

记一次20撸240的沙雕威胁情报提交(2019年老文)
0x01 起因 这是一篇沙雕文章,没什么技术含量,大家娱乐一下就好 前几个月,我的弟弟突然QQ给我发来了一条消息,说要买个QQ飞车的cdk,我作为一个通情达理的好哥哥,自然不好意思回绝,直接叫他发来…...

佳能镜头EOS系统EF协议逆向工程(三)解码算法
目录 数据结构 解码算法 解码效果 这篇文章基于上两篇文章继续, 佳能镜头EOS系统EF协议逆向工程(一)转接环电路设计_佳能ef自动对焦协议_岬淢箫声的博客-CSDN博客本文属于专栏——工业相机。此专栏首先提供我人工翻译的法语文档部分&…...

搞互联网吧,线下生意真不是人干的
搞互联网吧,线下生意真不是人干的 应该是正月初几里吧,好巧不巧的被迫去参加了一下我们初中同学的聚会。其实毕业这么多年,无论大学,高中还是中学,类似的聚会我都是能躲则躲,有特别想见的同学也都是私下单…...
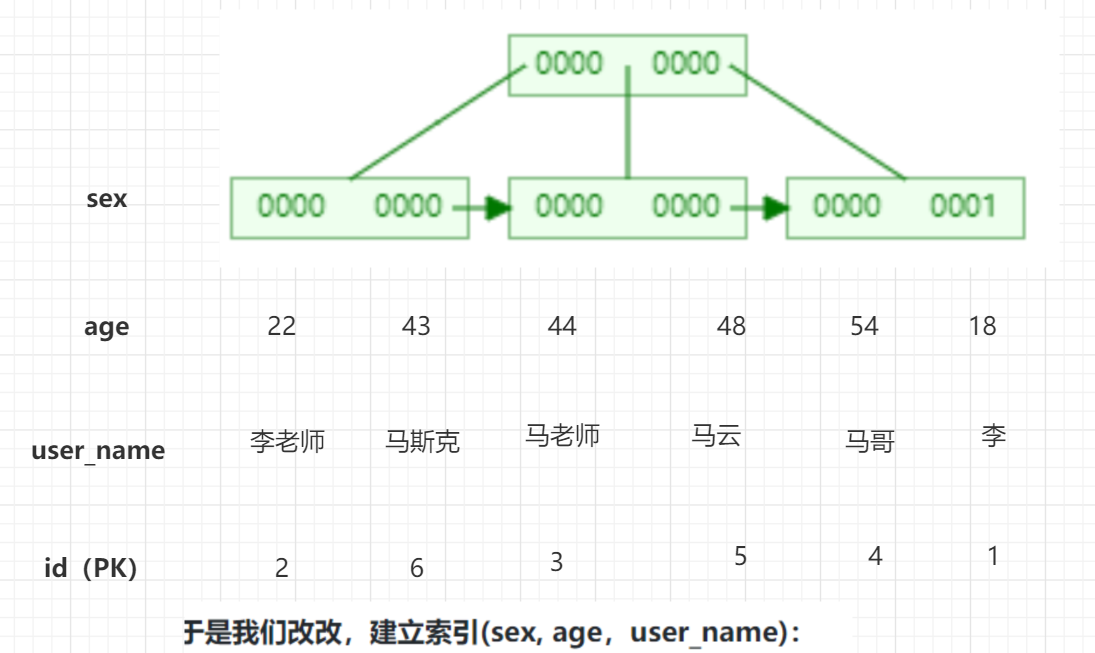
MySQL性能调优与设计——MySQL中的索引
MySQL中的索引 InnoDB存储引擎支持以下几种常见索引:B树索引、全文索引、哈希索引,其中比较关键的是B树索引。 B树索引 InnoDB中的索引自然也是按照B树来组织的,B树的叶子节点用来存放数据。 聚集索引/聚簇索引 InnoDB中使用了聚集索引&…...
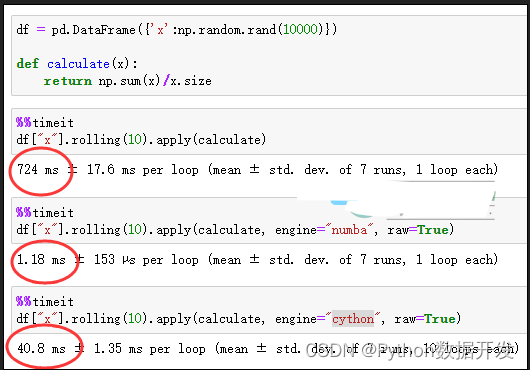
这5个代码技巧,让我的 Python 加速了很多倍
Python作为一种功能强大的编程语言,因其简单易学而受到很多初学者的青睐。它的应用领域又非常广泛:科学计算、游戏开发、爬虫、人工智能、自动化办公、Web应用开发等等。 而在数据科学领域中,Python 是使用最广泛的编程语言,并且…...

Sphinx+Scws 搭建千万级准实时搜索应用场景详解
目标: 一、搭建准确的千万级数据库的准实时搜索(见详情) 二、实现词语高亮(客户端JS渲染,服务器端渲染,详见7.3) 三、实现搜索联想(输入框onchange,ajax请求搜索,取10条在…...

kafka缩容后,使用tcpdump抓包找到还在连接的用户
1、使用tcpdump抓包监控端口9092 tcpdump src port 9092 16:23:27.680835 IP host01.XmlIpcRegSvc > 192.168.168.1.36199: Flags [R.], seq 0, ack 1493547965, win 0, length 0 16:23:27.681877 IP host01.XmlIpcRegSvc > 192.168.168.2.50416: Flags [R.], seq 0, ac…...

Spring
Spring Spring 是什么? Spring 是于 2003 年兴起的一个轻量级的,IOC 和 AOP 的 Java 开发框架,它 是为了简化企业级应用开发而生的。 Spring有几大特点如下 轻量级的 Spring 框架使用的 jar 都比较小,一般在 1M 以下或者几百 kb。Spring 核 心功能…...

vue2版本《后台管理模式》(中)
文章目录前言一、创建一个文件夹 utils 里面新增一个 setToken.js 文件(设置token验证)二 、创建一个api文件夹 新增 service.js (axios拦截器)三、在api文件夹里 新增一个 api.js 来接收数据(把api封装哪里需要某项数据直接引入就…...

网络游戏开发-服务器篇
1.网络 网络分为弱联网和强联网。 1.弱联网 弱联网是客户端连接到服务端发送一个请求,然后由服务端回应一个内容,这是单向传输的方式,服务端是无法主动给客户端发送消息的,服务端相应请求之后会自动关闭连接。 缺点:传输采用明文,通过抓包可以看到明文信息,安全性不太…...
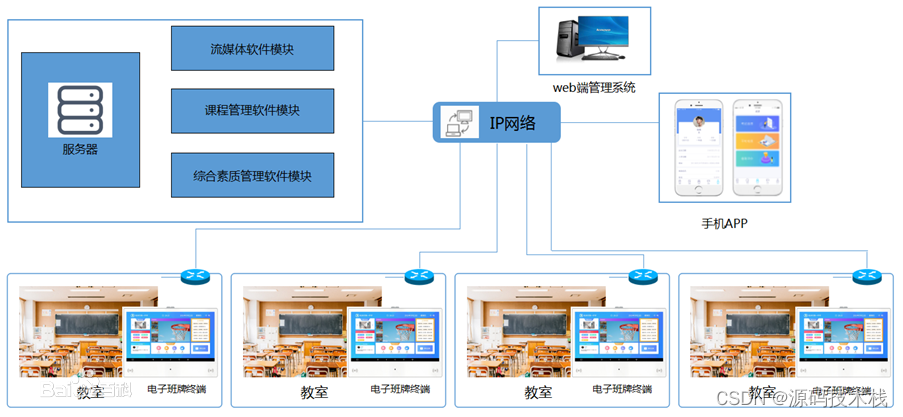
智慧校园源码:电子班牌,支持手机移动端以及web端对班牌设备的管控
▶ 智慧校园系统有源码,有演示! (电子班牌)设备管理: 1、 管理员查看全校电子班牌设备信息:含有(班级信息、软件版本、设备型号、开关机信息、班牌截屏信息、教室编号、设备ID、设备描述、在线状态、离线状…...
研报精选230216
目录 【行业230216东吴证券】环保行业月报:2023M1环卫新能源渗透率大增至11.91%,上海地区渗透率高达77%【行业230216国元证券】国元新食饮:一图君:22年白酒产量:同降6.2%【行业230216浙商证券】农林牧渔点评报告&#…...
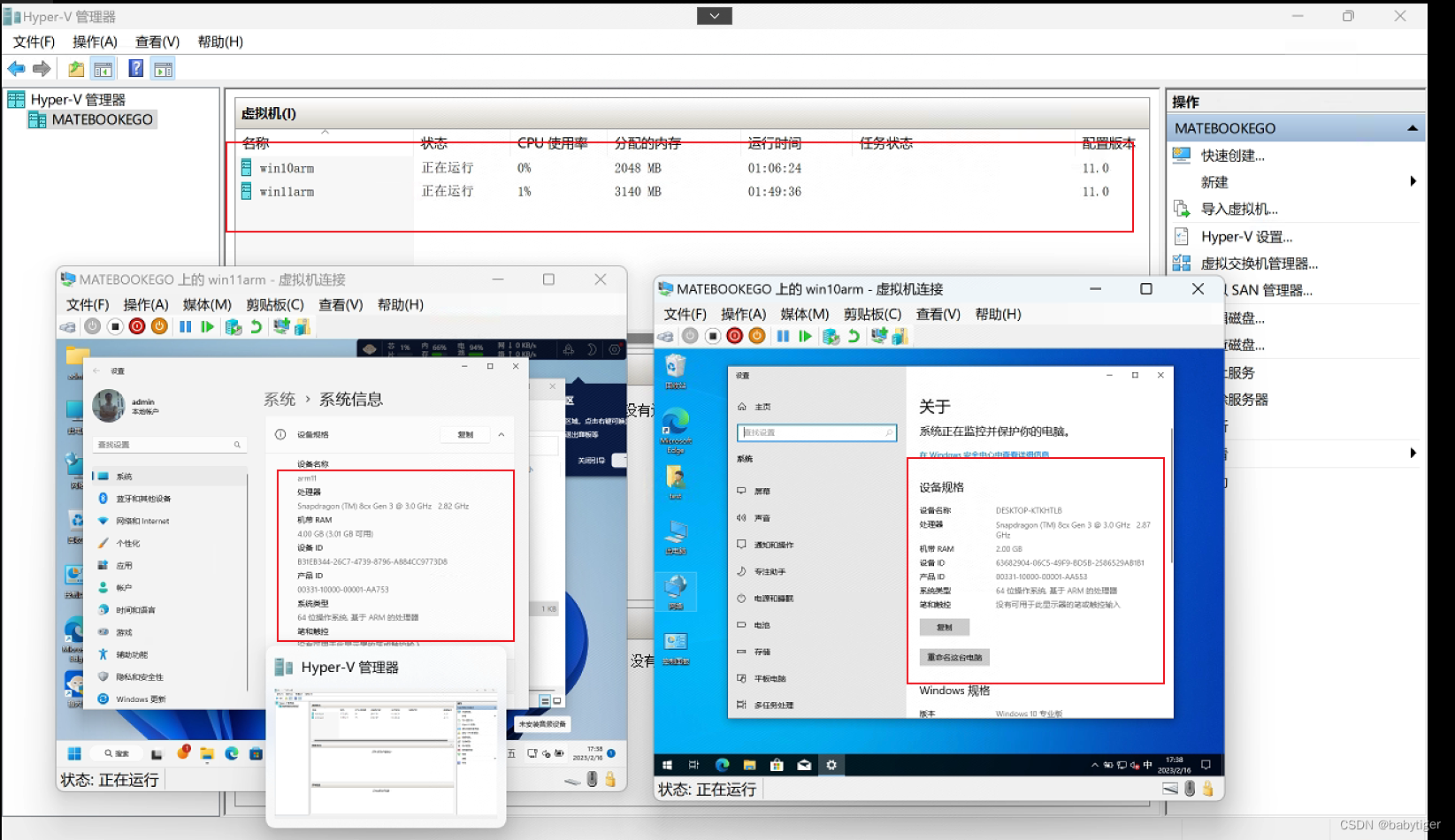
在华为MateBook Ego的arm windows 11上安装hyper-V虚拟机
入手一台华为matebook Ego的笔记本,由于想要测试一些arm的驱动功能,经常会把系统搞蓝屏,于是想安装一个虚拟机,于是试了vmware ,visual-box,由于本机是arm架构上面两个软件都无法进行正常安装,可能是由于有…...

web vue 项目 Docker化部署
Web 项目 Docker 化部署详细教程 目录 Web 项目 Docker 化部署概述Dockerfile 详解 构建阶段生产阶段 构建和运行 Docker 镜像 1. Web 项目 Docker 化部署概述 Docker 化部署的主要步骤分为以下几个阶段: 构建阶段(Build Stage):…...

调用支付宝接口响应40004 SYSTEM_ERROR问题排查
在对接支付宝API的时候,遇到了一些问题,记录一下排查过程。 Body:{"datadigital_fincloud_generalsaas_face_certify_initialize_response":{"msg":"Business Failed","code":"40004","sub_msg…...
:OpenBCI_GUI:从环境搭建到数据可视化(下))
脑机新手指南(八):OpenBCI_GUI:从环境搭建到数据可视化(下)
一、数据处理与分析实战 (一)实时滤波与参数调整 基础滤波操作 60Hz 工频滤波:勾选界面右侧 “60Hz” 复选框,可有效抑制电网干扰(适用于北美地区,欧洲用户可调整为 50Hz)。 平滑处理&…...

质量体系的重要
质量体系是为确保产品、服务或过程质量满足规定要求,由相互关联的要素构成的有机整体。其核心内容可归纳为以下五个方面: 🏛️ 一、组织架构与职责 质量体系明确组织内各部门、岗位的职责与权限,形成层级清晰的管理网络…...

DIY|Mac 搭建 ESP-IDF 开发环境及编译小智 AI
前一阵子在百度 AI 开发者大会上,看到基于小智 AI DIY 玩具的演示,感觉有点意思,想着自己也来试试。 如果只是想烧录现成的固件,乐鑫官方除了提供了 Windows 版本的 Flash 下载工具 之外,还提供了基于网页版的 ESP LA…...

NFT模式:数字资产确权与链游经济系统构建
NFT模式:数字资产确权与链游经济系统构建 ——从技术架构到可持续生态的范式革命 一、确权技术革新:构建可信数字资产基石 1. 区块链底层架构的进化 跨链互操作协议:基于LayerZero协议实现以太坊、Solana等公链资产互通,通过零知…...

Unit 1 深度强化学习简介
Deep RL Course ——Unit 1 Introduction 从理论和实践层面深入学习深度强化学习。学会使用知名的深度强化学习库,例如 Stable Baselines3、RL Baselines3 Zoo、Sample Factory 和 CleanRL。在独特的环境中训练智能体,比如 SnowballFight、Huggy the Do…...

3-11单元格区域边界定位(End属性)学习笔记
返回一个Range 对象,只读。该对象代表包含源区域的区域上端下端左端右端的最后一个单元格。等同于按键 End 向上键(End(xlUp))、End向下键(End(xlDown))、End向左键(End(xlToLeft)End向右键(End(xlToRight)) 注意:它移动的位置必须是相连的有内容的单元格…...

深入浅出深度学习基础:从感知机到全连接神经网络的核心原理与应用
文章目录 前言一、感知机 (Perceptron)1.1 基础介绍1.1.1 感知机是什么?1.1.2 感知机的工作原理 1.2 感知机的简单应用:基本逻辑门1.2.1 逻辑与 (Logic AND)1.2.2 逻辑或 (Logic OR)1.2.3 逻辑与非 (Logic NAND) 1.3 感知机的实现1.3.1 简单实现 (基于阈…...

MySQL 知识小结(一)
一、my.cnf配置详解 我们知道安装MySQL有两种方式来安装咱们的MySQL数据库,分别是二进制安装编译数据库或者使用三方yum来进行安装,第三方yum的安装相对于二进制压缩包的安装更快捷,但是文件存放起来数据比较冗余,用二进制能够更好管理咱们M…...
