「5」线性代数(期末复习)
🚀🚀🚀大家觉不错的话,就恳求大家点点关注,点点小爱心,指点指点🚀🚀🚀
目录
第四章 向量组的线性相关性
&5)向量空间
第五章 相似矩阵及二次型
&1)向量的内积、长度及正交性
第四章 向量组的线性相关性
&5)向量空间
第五章 相似矩阵及二次型
&1)向量的内积、长度及正交性
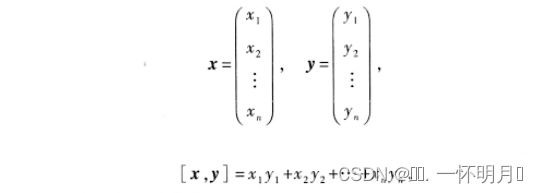
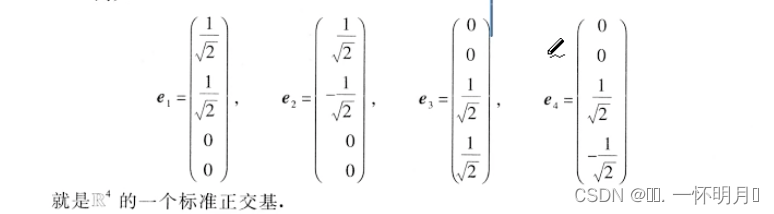

🌸🌸🌸如果大家还有不懂或者建议都可以发在评论区,我们共同探讨,共同学习,共同进步。谢谢大家! 🌸🌸🌸
相关文章:

「5」线性代数(期末复习)
🚀🚀🚀大家觉不错的话,就恳求大家点点关注,点点小爱心,指点指点🚀🚀🚀 目录 第四章 向量组的线性相关性 &5)向量空间 第五章 相似矩阵及二次型 &a…...

记一次20撸240的沙雕威胁情报提交(2019年老文)
0x01 起因 这是一篇沙雕文章,没什么技术含量,大家娱乐一下就好 前几个月,我的弟弟突然QQ给我发来了一条消息,说要买个QQ飞车的cdk,我作为一个通情达理的好哥哥,自然不好意思回绝,直接叫他发来…...

佳能镜头EOS系统EF协议逆向工程(三)解码算法
目录 数据结构 解码算法 解码效果 这篇文章基于上两篇文章继续, 佳能镜头EOS系统EF协议逆向工程(一)转接环电路设计_佳能ef自动对焦协议_岬淢箫声的博客-CSDN博客本文属于专栏——工业相机。此专栏首先提供我人工翻译的法语文档部分&…...

搞互联网吧,线下生意真不是人干的
搞互联网吧,线下生意真不是人干的 应该是正月初几里吧,好巧不巧的被迫去参加了一下我们初中同学的聚会。其实毕业这么多年,无论大学,高中还是中学,类似的聚会我都是能躲则躲,有特别想见的同学也都是私下单…...
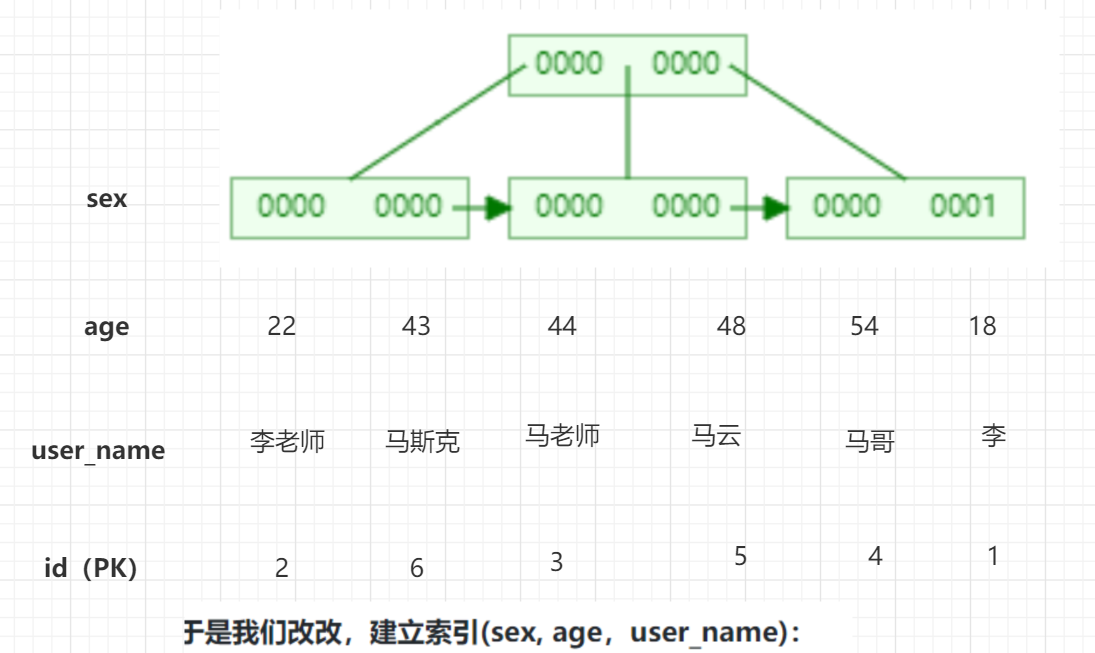
MySQL性能调优与设计——MySQL中的索引
MySQL中的索引 InnoDB存储引擎支持以下几种常见索引:B树索引、全文索引、哈希索引,其中比较关键的是B树索引。 B树索引 InnoDB中的索引自然也是按照B树来组织的,B树的叶子节点用来存放数据。 聚集索引/聚簇索引 InnoDB中使用了聚集索引&…...
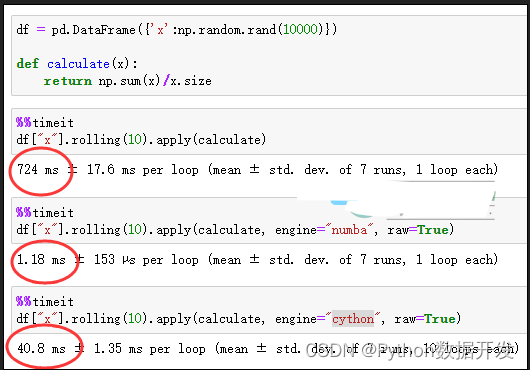
这5个代码技巧,让我的 Python 加速了很多倍
Python作为一种功能强大的编程语言,因其简单易学而受到很多初学者的青睐。它的应用领域又非常广泛:科学计算、游戏开发、爬虫、人工智能、自动化办公、Web应用开发等等。 而在数据科学领域中,Python 是使用最广泛的编程语言,并且…...

Sphinx+Scws 搭建千万级准实时搜索应用场景详解
目标: 一、搭建准确的千万级数据库的准实时搜索(见详情) 二、实现词语高亮(客户端JS渲染,服务器端渲染,详见7.3) 三、实现搜索联想(输入框onchange,ajax请求搜索,取10条在…...

kafka缩容后,使用tcpdump抓包找到还在连接的用户
1、使用tcpdump抓包监控端口9092 tcpdump src port 9092 16:23:27.680835 IP host01.XmlIpcRegSvc > 192.168.168.1.36199: Flags [R.], seq 0, ack 1493547965, win 0, length 0 16:23:27.681877 IP host01.XmlIpcRegSvc > 192.168.168.2.50416: Flags [R.], seq 0, ac…...

Spring
Spring Spring 是什么? Spring 是于 2003 年兴起的一个轻量级的,IOC 和 AOP 的 Java 开发框架,它 是为了简化企业级应用开发而生的。 Spring有几大特点如下 轻量级的 Spring 框架使用的 jar 都比较小,一般在 1M 以下或者几百 kb。Spring 核 心功能…...

vue2版本《后台管理模式》(中)
文章目录前言一、创建一个文件夹 utils 里面新增一个 setToken.js 文件(设置token验证)二 、创建一个api文件夹 新增 service.js (axios拦截器)三、在api文件夹里 新增一个 api.js 来接收数据(把api封装哪里需要某项数据直接引入就…...

网络游戏开发-服务器篇
1.网络 网络分为弱联网和强联网。 1.弱联网 弱联网是客户端连接到服务端发送一个请求,然后由服务端回应一个内容,这是单向传输的方式,服务端是无法主动给客户端发送消息的,服务端相应请求之后会自动关闭连接。 缺点:传输采用明文,通过抓包可以看到明文信息,安全性不太…...
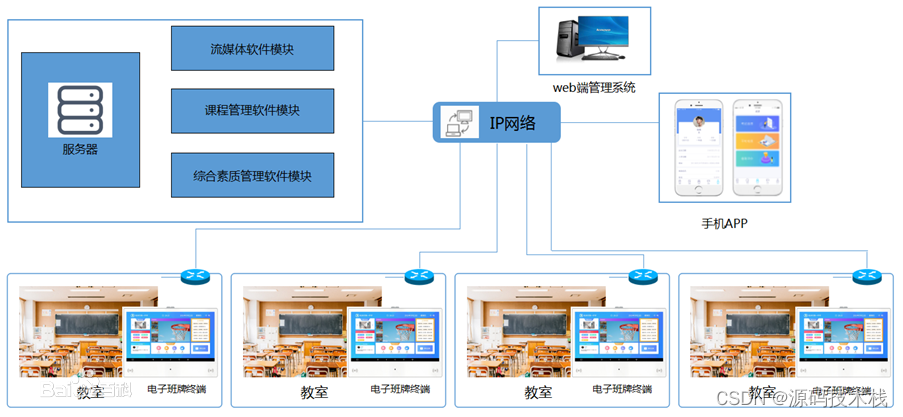
智慧校园源码:电子班牌,支持手机移动端以及web端对班牌设备的管控
▶ 智慧校园系统有源码,有演示! (电子班牌)设备管理: 1、 管理员查看全校电子班牌设备信息:含有(班级信息、软件版本、设备型号、开关机信息、班牌截屏信息、教室编号、设备ID、设备描述、在线状态、离线状…...
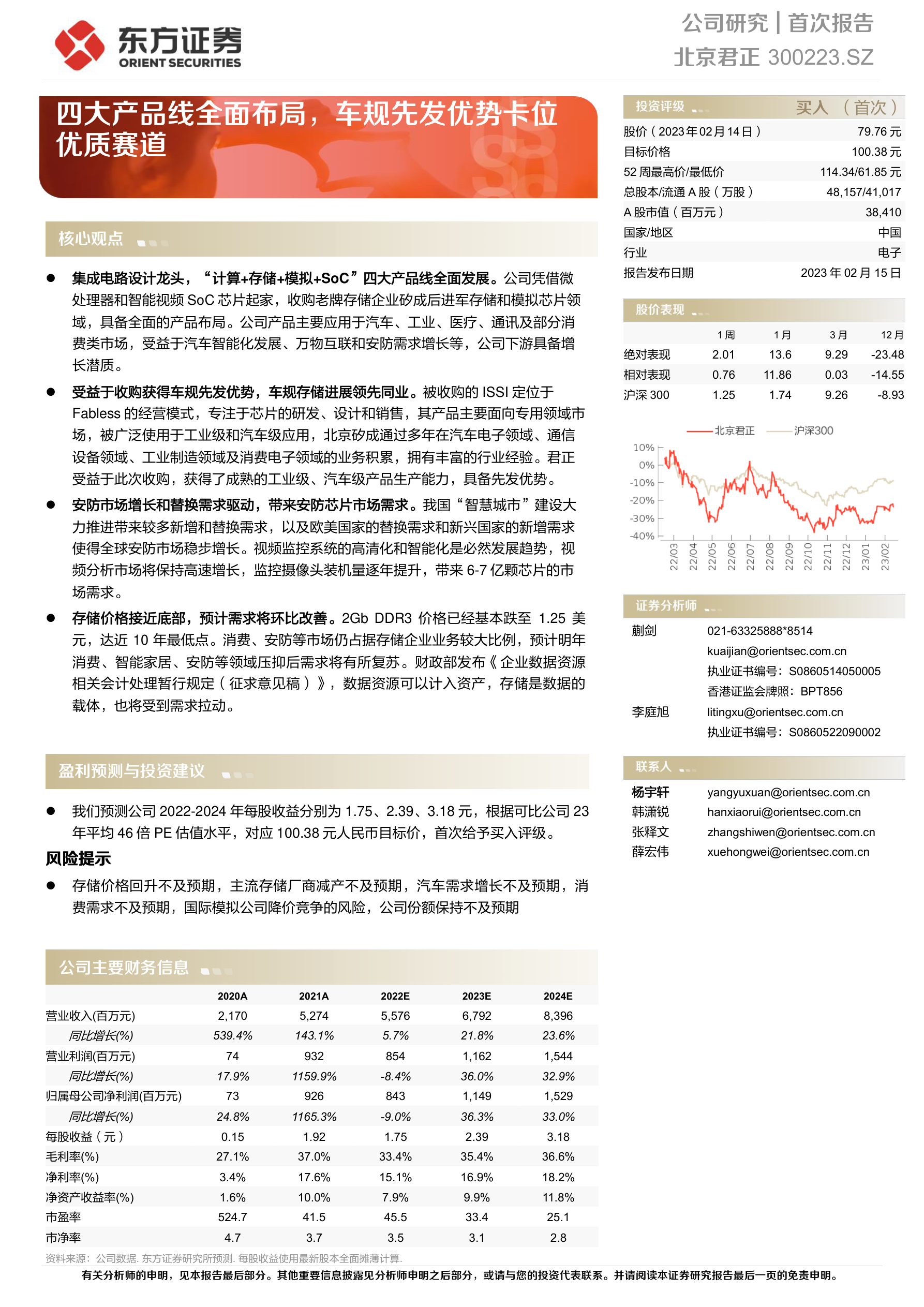
研报精选230216
目录 【行业230216东吴证券】环保行业月报:2023M1环卫新能源渗透率大增至11.91%,上海地区渗透率高达77%【行业230216国元证券】国元新食饮:一图君:22年白酒产量:同降6.2%【行业230216浙商证券】农林牧渔点评报告&#…...
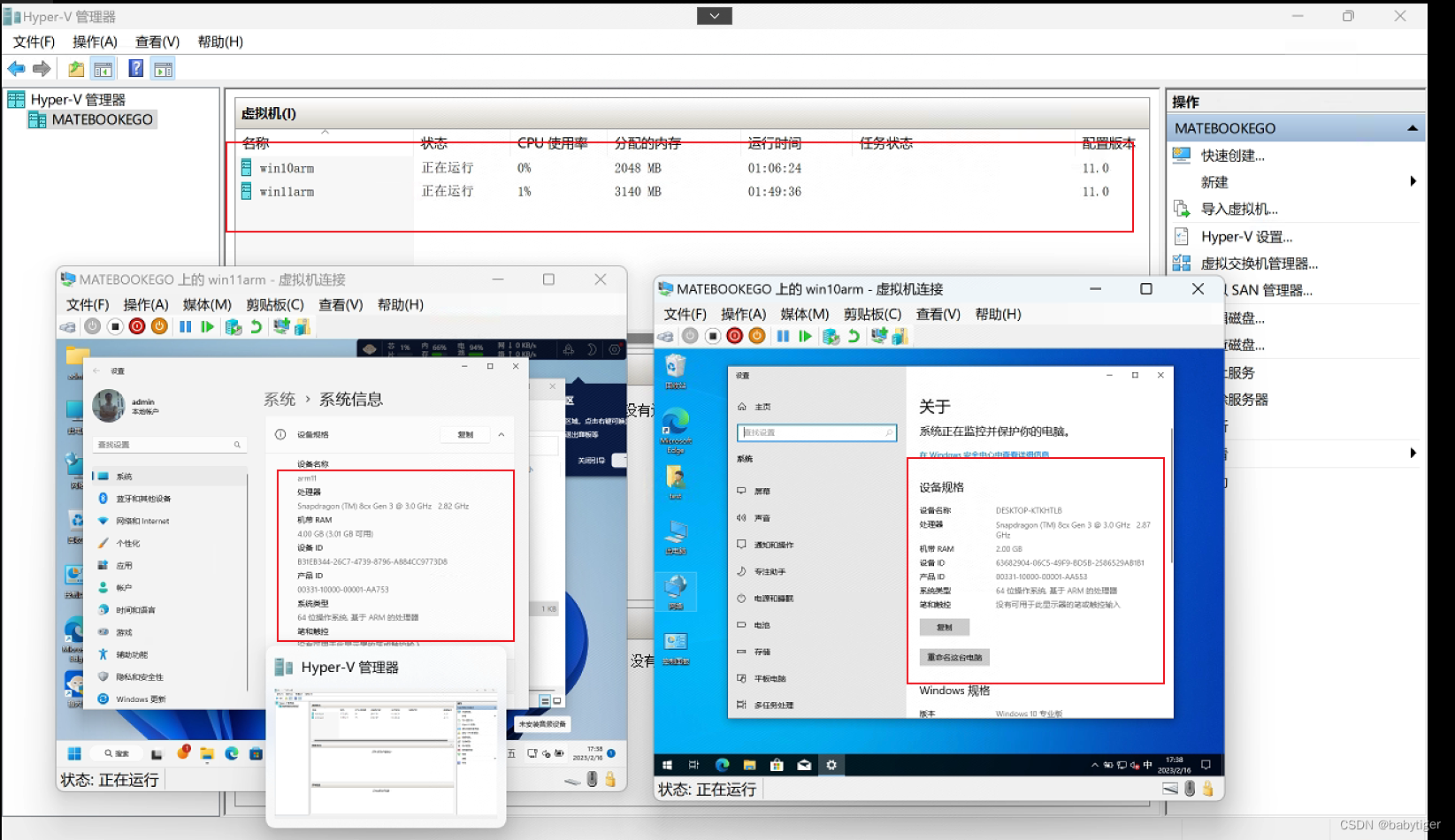
在华为MateBook Ego的arm windows 11上安装hyper-V虚拟机
入手一台华为matebook Ego的笔记本,由于想要测试一些arm的驱动功能,经常会把系统搞蓝屏,于是想安装一个虚拟机,于是试了vmware ,visual-box,由于本机是arm架构上面两个软件都无法进行正常安装,可能是由于有…...

OpenCV Canny边缘检测
本文是OpenCV图像视觉入门之路的第13篇文章,本文详细的介绍了Canny边缘检测算子的各种操作,例如:Canny算子进行边缘检测等操作。 Canny函数是OpenCV中用于执行边缘检测的函数之一,其参数包括: threshold1:…...

C#.Net正则表达式学习笔记
C#.Net正则表达式学习笔记 在处理字符串时,你会经常有查找符合特定条件的字符串的需求,比如判断一串电话号码是否符合格式、一个邮箱是否符合格式、一个密码是否包含了字母大小写等等。 正则表达式(Regular expressions)用于匹配文本,使用一…...

矩阵理论复习(十二)
已知方阵A的不变因子: 求谱半径求矩阵级数判断矩阵幂级数的收敛性 若矩阵B的某个算子范数小于1,则I-B可逆。 矩阵分析 任何相容矩阵范数都存在与之相容的向量范数。 盖尔圆盘定理一的证明 椭圆范数的证明 若||.||是Cm上的向量范数,A为…...
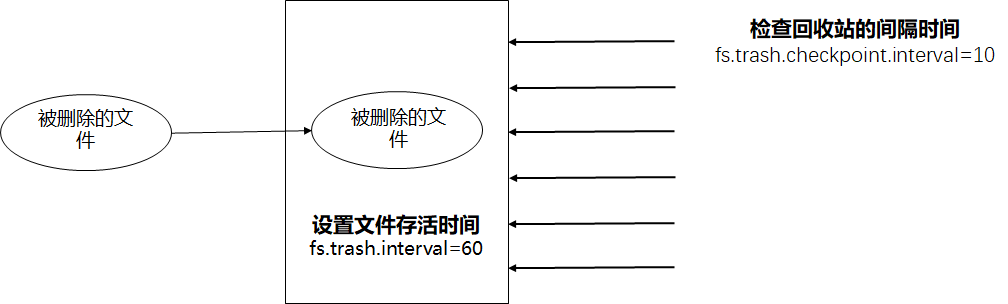
大数据框架之Hadoop:HDFS(七)HDFS 2.X新特性
7.1集群间数据拷贝 scp实现两个远程主机之间的文件复制 scp -r hello.txt roothadoop103:/root/hello.txt // 推 push scp -r roothadoop103:/root/hello.txt hello.txt // 拉 pull scp -r roothadoop103:/root/hello.txt roothadoop104:/root //是通过本地主机中…...
Fluent工作目录
1 工作目录定义工作目录(working directory)是一种文件存储路径设置方式。基于工作目录的方法,写文件时只需要指定文件名,而不需要指定完全的文件路径,从而简化程序编写,对不同操作系统环境有更好的适应性。…...

Learning C++ No.10【STL No.2】
引言: 北京时间:2023/2/14/23:18,放假两个月,没有锻炼,今天去跑了几圈,一个字,累,感觉人都要原地升天了,所以各位小伙伴,准确的说是各位卷王,一定…...

XML Group端口详解
在XML数据映射过程中,经常需要对数据进行分组聚合操作。例如,当处理包含多个物料明细的XML文件时,可能需要将相同物料号的明细归为一组,或对相同物料号的数量进行求和计算。传统实现方式通常需要编写脚本代码,增加了开…...

vscode里如何用git
打开vs终端执行如下: 1 初始化 Git 仓库(如果尚未初始化) git init 2 添加文件到 Git 仓库 git add . 3 使用 git commit 命令来提交你的更改。确保在提交时加上一个有用的消息。 git commit -m "备注信息" 4 …...
)
Java 语言特性(面试系列1)
一、面向对象编程 1. 封装(Encapsulation) 定义:将数据(属性)和操作数据的方法绑定在一起,通过访问控制符(private、protected、public)隐藏内部实现细节。示例: public …...

[ICLR 2022]How Much Can CLIP Benefit Vision-and-Language Tasks?
论文网址:pdf 英文是纯手打的!论文原文的summarizing and paraphrasing。可能会出现难以避免的拼写错误和语法错误,若有发现欢迎评论指正!文章偏向于笔记,谨慎食用 目录 1. 心得 2. 论文逐段精读 2.1. Abstract 2…...

基础测试工具使用经验
背景 vtune,perf, nsight system等基础测试工具,都是用过的,但是没有记录,都逐渐忘了。所以写这篇博客总结记录一下,只要以后发现新的用法,就记得来编辑补充一下 perf 比较基础的用法: 先改这…...

【单片机期末】单片机系统设计
主要内容:系统状态机,系统时基,系统需求分析,系统构建,系统状态流图 一、题目要求 二、绘制系统状态流图 题目:根据上述描述绘制系统状态流图,注明状态转移条件及方向。 三、利用定时器产生时…...
)
【服务器压力测试】本地PC电脑作为服务器运行时出现卡顿和资源紧张(Windows/Linux)
要让本地PC电脑作为服务器运行时出现卡顿和资源紧张的情况,可以通过以下几种方式模拟或触发: 1. 增加CPU负载 运行大量计算密集型任务,例如: 使用多线程循环执行复杂计算(如数学运算、加密解密等)。运行图…...

OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别
OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别 直接训练提示词嵌入向量的核心区别 您提到的代码: prompt_embedding = initial_embedding.clone().requires_grad_(True) optimizer = torch.optim.Adam([prompt_embedding...

什么是Ansible Jinja2
理解 Ansible Jinja2 模板 Ansible 是一款功能强大的开源自动化工具,可让您无缝地管理和配置系统。Ansible 的一大亮点是它使用 Jinja2 模板,允许您根据变量数据动态生成文件、配置设置和脚本。本文将向您介绍 Ansible 中的 Jinja2 模板,并通…...

并发编程 - go版
1.并发编程基础概念 进程和线程 A. 进程是程序在操作系统中的一次执行过程,系统进行资源分配和调度的一个独立单位。B. 线程是进程的一个执行实体,是CPU调度和分派的基本单位,它是比进程更小的能独立运行的基本单位。C.一个进程可以创建和撤销多个线程;同一个进程中…...
