OJ练习第127题——统计范围内的元音字符串数
统计范围内的元音字符串数
力扣链接:2559. 统计范围内的元音字符串数
题目描述
给你一个下标从 0 开始的字符串数组 words 以及一个二维整数数组 queries 。
每个查询 queries[i] = [li, ri] 会要求我们统计在 words 中下标在 li 到 ri 范围内(包含 这两个值)并且以元音开头和结尾的字符串的数目。
返回一个整数数组,其中数组的第 i 个元素对应第 i 个查询的答案。
注意:元音字母是 ‘a’、‘e’、‘i’、‘o’ 和 ‘u’ 。
示例
示例 1:
输入:words = [“aba”,“bcb”,“ece”,“aa”,“e”], queries = [[0,2],[1,4],[1,1]]
输出:[2,3,0]
解释:以元音开头和结尾的字符串是 “aba”、“ece”、“aa” 和 “e” 。
查询 [0,2] 结果为 2(字符串 “aba” 和 “ece”)。
查询 [1,4] 结果为 3(字符串 “ece”、“aa”、“e”)。
查询 [1,1] 结果为 0 。
返回结果 [2,3,0] 。
示例 2:
输入:words = [“a”,“e”,“i”], queries = [[0,2],[0,1],[2,2]]
输出:[3,2,1]
解释:每个字符串都满足这一条件,所以返回 [3,2,1] 。
Java代码
class Solution {public int[] vowelStrings(String[] words, int[][] queries) {int n = words.length;int[] prefixSums = new int[n + 1];for (int i = 0; i < n; i++) {int value = isVowelString(words[i]) ? 1 : 0;prefixSums[i + 1] = prefixSums[i] + value;}int q = queries.length;int[] ans = new int[q];for (int i = 0; i < q; i++) {int start = queries[i][0], end = queries[i][1];ans[i] = prefixSums[end + 1] - prefixSums[start];}return ans;}public boolean isVowelString(String word) {return isVowelLetter(word.charAt(0)) && isVowelLetter(word.charAt(word.length() - 1));}public boolean isVowelLetter(char c) {return c == 'a' || c == 'e' || c == 'i' || c == 'o' || c == 'u';}
}来源:力扣(LeetCode)
链接:https://leetcode.cn/problems/count-vowel-strings-in-ranges
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
相关文章:

OJ练习第127题——统计范围内的元音字符串数
统计范围内的元音字符串数 力扣链接:2559. 统计范围内的元音字符串数 题目描述 给你一个下标从 0 开始的字符串数组 words 以及一个二维整数数组 queries 。 每个查询 queries[i] [li, ri] 会要求我们统计在 words 中下标在 li 到 ri 范围内(包含 这…...
图片优化: CssSprites与Base64编码
文章目录 1 css sprites1.1 CSS Sprites是什么1.2 为什么需要css sprites1.3 优势1.4 使用原理1.5 DEMO 2 图片Base64编码 1 css sprites 1.1 CSS Sprites是什么 CSS Sprites是一种网页图片应用处理方式。 又被解释为: CSS精灵CSS图像拼合CSS贴图定位CSS图片精灵…...

JavaScript中的Map、WeakMap和Object的区别
Map Map是一种新的数据结构,它允许使用任何数据类型(包括对象和基本数据类型)作为键。 Map的一些特性包括: 保持键的插入顺序:当遍历Map时,键值对会按照插入顺序返回。键可以是任意类型:与Obj…...

华为OD机试之打印机队列(Java源码)
打印机队列 题目描述 有5台打印机打印文件,每台打印机有自己的待打印队列。 因为打印的文件内容有轻重缓急之分,所以队列中的文件有1~10不同的代先级,其中 数字越大优先级越高 打印机会从自己的待打印队列中选择优先级最高的文件来打印。 如…...

分享一个国内免费的ChatGPT网站,手机电脑通用,免费无限制,支持AI绘画
背景 ChatGPT作为一种基于人工智能技术的自然语言处理工具,近期的热度直接沸腾🌋。 作为一个AI爱好者,翻遍了各大基于ChatGPT的网站,终于找到一个免费!免登陆!手机电脑通用!国内可直接对话的C…...

【面向对象编程1】——类和对象——如桃花来
目录索引 面向过程和面向对象的区别:面向过程:面向对象:总结: 类和对象:定义类:语法: 创建对象:实例演示: 魔法方法:__init __方法:__ del __方法…...
chat聊天系统消息消费时遇到的问题及优化思路(二)
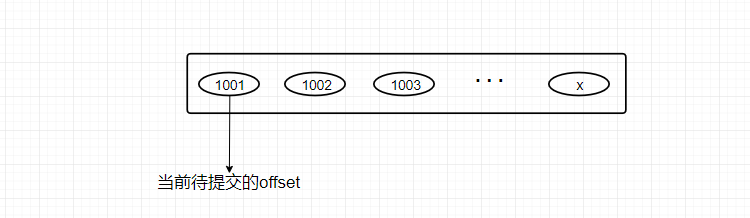
1、前言 考虑下面几个条件下如何提升kafka的消费速度 消息要求严格有序,如chat聊天消息业务处理速度慢,如处理一条数据需要100ms分片不合理,如有的分区很闲,有的分区消息数量积压 2、解决方案 1、顺序问题 关于消息消费时存在…...

js正则中的match()
在前端开发中,正则表达式是一大利器。所以我们这次就来讨论下match()方法。 match本身是JavaScript语言中字符串对象的一个方法,该方法的签名是 match([string] | [RegExp]) 它的参数既可以是一个字符串,也可以是一个正则表达式。该方法绝…...
Apache 配置和应用
目录 构建虚拟 Web 主机 Options指令解释 Options指令常用选项 AllowOverride指令解释: 地址限制策略: httpd服务支持的虚拟主机类型包括以下三种: 基于域名的虚拟主机 1.为虚拟主机提供域名解析 2.为虚拟主机准备网页文档 3.添加虚拟…...

实现PyTorch/ONNX自定义节点操作的TensorRT部署
参考一 下面是基本步骤: 加载训练好的bev transformer网络权重参数: import torch from model import Modelmodel Model() model.load_state_dict(torch.load("path/to/weights"))定义新的自定义操作: import torch from torc…...

Shamir 秘密共享、GMW和BGW方案
一、Shamir秘密共享 Shamir秘密共享方案是一种将秘密拆分成多份并分配给多个参与者保存,只有在满足特定条件下才能恢复原始秘密的密码学方案。它具有良好的容错性、加法同态性和无条件安全性等特点。 具体地,Shamir秘密共享方案可以概括为以下步骤&…...

Day56【动态规划】583.两个字符串的删除操作、72.编辑距离
583.两个字符串的删除操作 力扣题目链接/文章讲解 视频讲解 1、确定 dp 数组下标及值含义 dp[i][j]:以下标 i 为结尾的字符串 word1,和以下标 j 为结尾的字符串 word2,想要达到相等,所需要删除元素的最少次数为 dp[i][j] 2、…...

Arnold图像置乱的MATLAB实现
这件事情的起因是这样的,我需要研究一下各种图像置乱的算法。然后在知乎上找到了一篇关于Arnold变化的文章,但是呢,这个人实际上是卖资料,代做大作业的。详细的代码根部不给你,则给我气坏了,必须要手动实现…...
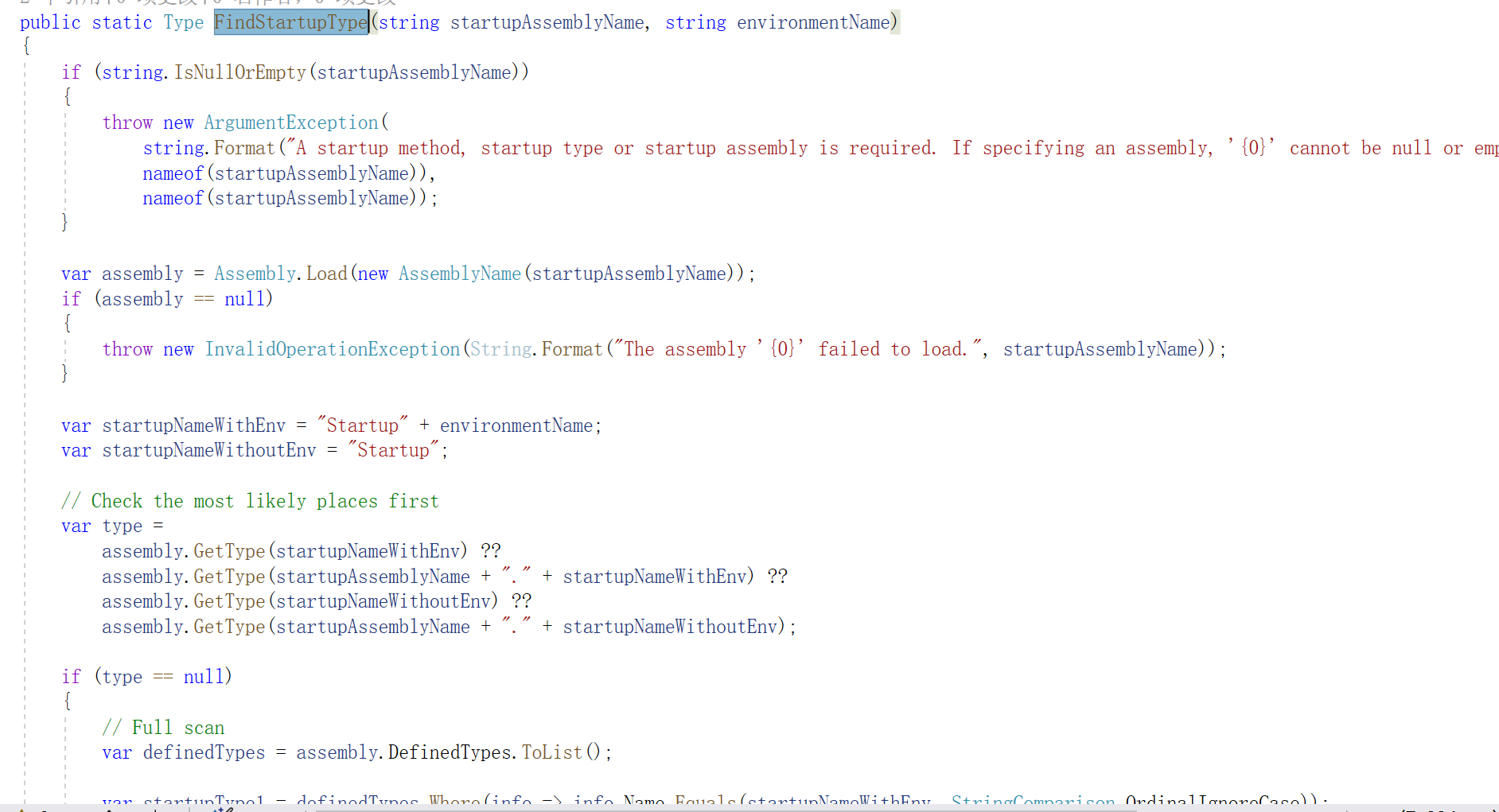
ASP.NET Core
1. 入口文件 一个应用程序总有一个入口文件,是应用启动代码开始执行的地方,这里往往也会涉及到应用的各种配置。当我们接触到一个新框架的时候,可以从入口文件入手,了解入口文件,能够帮助我们更好地理解应用的相关配置…...
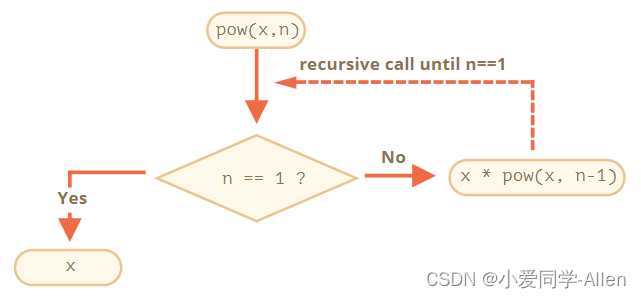
javascript基础二十二:举例说明你对尾递归的理解,有哪些应用场景
一、递归 递归(英语:Recursion) 在数学与计算机科学中,是指在函数的定义中使用函数自身的方法 在函数内部,可以调用其他函数。如果一个函数在内部调用自身本身,这个函数就是递归函数 其核心思想是把一个大型…...
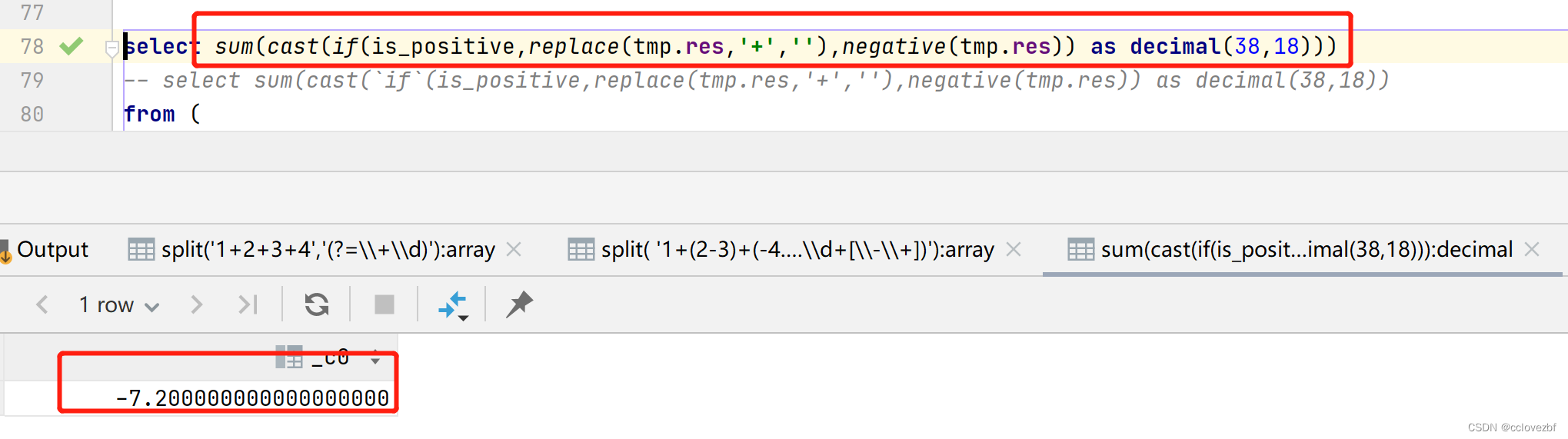
hive中如何计算字符串中表达式
比如 select 1(2-3)(-4.1-3.1)-(4-3)-(-3.34.3)-1 col ,1(2-3)(-4.1-3.1)-(4-3)-(-3.34.3)-1 result \ 现在的需求式 给你一个字符串如上述col 你要算出result。 前提式 只有和-的运算,而且只有嵌套一次 -(4-3)没有 -(-4(3-(31)))嵌套多次。 第一步我们需要将运…...

如何将maven项目改为springboot项目?
将 Maven 项目转换为 Spring Boot 项目需要进行以下步骤: 1. 在 Maven 项目中添加 Spring Boot 的依赖。可以通过在 pom.xml 文件中添加以下依赖来实现: <dependency> <groupId>org.springframework.boot</groupId> <artifactId>…...
:哈希查找)
Java与查找算法(5):哈希查找
一、哈希查找 哈希查找,也称为散列查找,是一种基于哈希表的查找算法。哈希表是一种数据结构,它将键(key)映射到值(value),使得查找某个键对应的值的时间复杂度为O(1)。哈希查找的过…...
Vercel部署个人博客
vercel 部署静态资源网站极其方便简单,并且有可观的访问速度,最主要的是免费部署。 如果你还没有尝试的话,强烈建议去使用一下。 演示博客演示http://202271.xyz/?vercel vercel 介绍 注册账号 进入Vercel官网https://vercel.com&#x…...
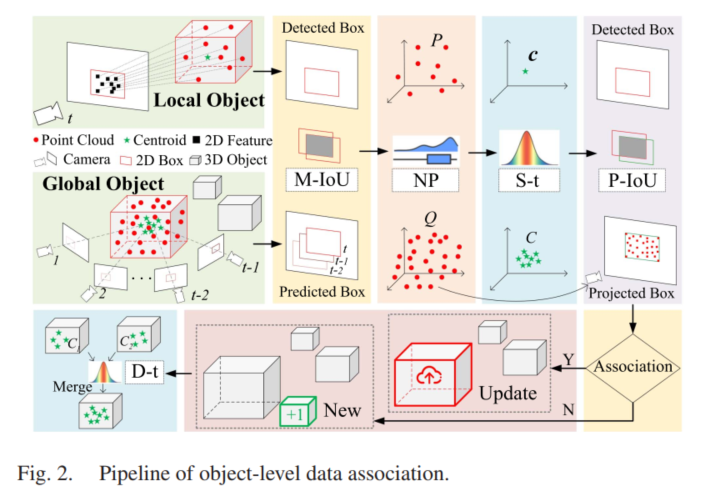
【论文阅读】An Object SLAM Framework for Association, Mapping, and High-Level Tasks
一、系统概述 这篇文章是一个十分完整的物体级SLAM框架,偏重于建图及高层应用,在前端的部分使用了ORBSLAM作为基础框架,用于提供点云以及相机的位姿,需要注意的是,这篇文章使用的是相机,虽然用的是点云这个…...

Linux 文件类型,目录与路径,文件与目录管理
文件类型 后面的字符表示文件类型标志 普通文件:-(纯文本文件,二进制文件,数据格式文件) 如文本文件、图片、程序文件等。 目录文件:d(directory) 用来存放其他文件或子目录。 设备…...
)
rknn优化教程(二)
文章目录 1. 前述2. 三方库的封装2.1 xrepo中的库2.2 xrepo之外的库2.2.1 opencv2.2.2 rknnrt2.2.3 spdlog 3. rknn_engine库 1. 前述 OK,开始写第二篇的内容了。这篇博客主要能写一下: 如何给一些三方库按照xmake方式进行封装,供调用如何按…...

Auto-Coder使用GPT-4o完成:在用TabPFN这个模型构建一个预测未来3天涨跌的分类任务
通过akshare库,获取股票数据,并生成TabPFN这个模型 可以识别、处理的格式,写一个完整的预处理示例,并构建一个预测未来 3 天股价涨跌的分类任务 用TabPFN这个模型构建一个预测未来 3 天股价涨跌的分类任务,进行预测并输…...

《通信之道——从微积分到 5G》读书总结
第1章 绪 论 1.1 这是一本什么样的书 通信技术,说到底就是数学。 那些最基础、最本质的部分。 1.2 什么是通信 通信 发送方 接收方 承载信息的信号 解调出其中承载的信息 信息在发送方那里被加工成信号(调制) 把信息从信号中抽取出来&am…...

SpringBoot+uniapp 的 Champion 俱乐部微信小程序设计与实现,论文初版实现
摘要 本论文旨在设计并实现基于 SpringBoot 和 uniapp 的 Champion 俱乐部微信小程序,以满足俱乐部线上活动推广、会员管理、社交互动等需求。通过 SpringBoot 搭建后端服务,提供稳定高效的数据处理与业务逻辑支持;利用 uniapp 实现跨平台前…...

现代密码学 | 椭圆曲线密码学—附py代码
Elliptic Curve Cryptography 椭圆曲线密码学(ECC)是一种基于有限域上椭圆曲线数学特性的公钥加密技术。其核心原理涉及椭圆曲线的代数性质、离散对数问题以及有限域上的运算。 椭圆曲线密码学是多种数字签名算法的基础,例如椭圆曲线数字签…...

【OSG学习笔记】Day 16: 骨骼动画与蒙皮(osgAnimation)
骨骼动画基础 骨骼动画是 3D 计算机图形中常用的技术,它通过以下两个主要组件实现角色动画。 骨骼系统 (Skeleton):由层级结构的骨头组成,类似于人体骨骼蒙皮 (Mesh Skinning):将模型网格顶点绑定到骨骼上,使骨骼移动…...

tree 树组件大数据卡顿问题优化
问题背景 项目中有用到树组件用来做文件目录,但是由于这个树组件的节点越来越多,导致页面在滚动这个树组件的时候浏览器就很容易卡死。这种问题基本上都是因为dom节点太多,导致的浏览器卡顿,这里很明显就需要用到虚拟列表的技术&…...

LOOI机器人的技术实现解析:从手势识别到边缘检测
LOOI机器人作为一款创新的AI硬件产品,通过将智能手机转变为具有情感交互能力的桌面机器人,展示了前沿AI技术与传统硬件设计的完美结合。作为AI与玩具领域的专家,我将全面解析LOOI的技术实现架构,特别是其手势识别、物体识别和环境…...

Ubuntu系统复制(U盘-电脑硬盘)
所需环境 电脑自带硬盘:1块 (1T) U盘1:Ubuntu系统引导盘(用于“U盘2”复制到“电脑自带硬盘”) U盘2:Ubuntu系统盘(1T,用于被复制) !!!建议“电脑…...
