题解2023.6.5
D - Factorial Divisibility
对于a[i]>=x的数一定可以整除,考虑a[i]<x的数,因为(x+1)*x! = (x+1)!
统计ai出现的次数, 把他转换为大的阶乘, 如果, 最终1到x - 1, ai的出现次数均为0则说明可以被x!整除
#pragma GCC optimize(2)
#pragma GCC optimize(3)
#pragma GCC optimize(fast)
#include<iostream>
#include<algorithm>
#include<map>
#include<set>
#include<queue>
#include<cstring>
#include<math.h>
#include<map>
#include<vector>
#include<stack>
#define ms(x,y) memset(x,y,sizeof x);
#define YES cout<<"YES"<<'\n';
#define NO cout<<"NO"<<'\n';
#define endl cout<<'\n';
typedef long long ll;
const int maxn = 5e5 + 100, inf = 1e18;
const int mod = 1e9 + 7;
using namespace std;
ll a[maxn];
void solve() {int n, x;cin >> n >> x;map<int, int>mp;for (int i = 1; i <= n; i++) {int y;cin >> y;mp[y]++;}for (int i = 1; i < x; i++) {mp[i + 1] += (mp[i] / (i + 1));mp[i] = mp[i] % (i + 1);}for (int i = 1; i < x;i++) {if (mp[i] != 0) {NOreturn;}}YES
}
signed main()
{ios::sync_with_stdio(false);solve();
}C1 - Make Nonzero Sum (easy version)
思路:奇数一定不可以,偶数一定可以,两两相同放一起,不同分开
#pragma GCC optimize(2)
#pragma GCC optimize(3)
#pragma GCC optimize(fast)
#include<iostream>
#include<algorithm>
#include<map>
#include<set>
#include<queue>
#include<cstring>
#include<math.h>
#include<map>
#include<vector>
#include<stack>
#define ms(x,y) memset(x,y,sizeof x);
#define YES cout<<"YES"<<'\n';
#define NO cout<<"NO"<<'\n';
#define endl cout<<'\n';
typedef long long ll;
const int maxn=2e5+10,inf = 1e18 ;
const int mod = 1e9 + 7;
using namespace std;
int a[maxn];
struct node {int l, r;
}x[maxn];void solve(){int n;cin >> n;for (int i = 1; i <= n; i++) {cin >> a[i];}if (n & 1) {cout << -1 << '\n';return;}int cnt = 0;for (int i = 1; i <= n; i += 2) {if (a[i] == a[i + 1]) {x[++cnt].l = i;x[cnt].r = i + 1;}else {x[++cnt].l = i;x[cnt].r = i;x[++cnt].l = i + 1;x[cnt].r = i + 1;}}cout << cnt << '\n';for (int i = 1; i <= cnt; i++) {cout << x[i].l << ' ' << x[i].r << '\n';}}
signed main()
{ios::sync_with_stdio(false);int t;cin >> t;while (t--) {solve();}
}
C2. Make Nonzero Sum (hard version)
思路:变成了0,1,-1三种情况,对于去除0后为奇数的一定不可以,偶数的一定可以,
和(easy version)情况相似,相邻的不为0的凑在一起
#pragma GCC optimize(2)
#pragma GCC optimize(3)
#pragma GCC optimize(fast)
#include<iostream>
#include<algorithm>
#include<map>
#include<set>
#include<queue>
#include<cstring>
#include<math.h>
#include<map>
#include<vector>
#include<stack>
using namespace std;
#define ll long long
#define pcc pair<char, char>
#define pii pair<int, int>
#define inf 0x3f3f3f3f
const int maxn = 200010;
int n, a[maxn];
void solve() {cin >> n;int cnt = 0;for (int i = 1; i <= n; ++i) {cin >> a[i];if (a[i]) ++cnt;}if (cnt & 1) {cout << -1 << '\n';return;}vector<pii> res;int l, r;for (int i = 1; i <= n;) {while (i <= n && !a[i]) {res.push_back({ i, i });++i;}if (i > n) {break;}l = i;r = i + 1;if (a[r]) { if (a[l] == a[r]) {res.push_back({ l, r });}else {res.push_back({ l, l });res.push_back({ r, r });}}else {res.push_back({ l, l });while (r <= n && !a[r]) {res.push_back({ r, r });++r;}if (a[l] == a[r]) {res.back().second = r;}else {res.push_back({ r, r });}}i = r + 1;}int len = res.size();cout << len << '\n';for (auto p : res) {cout << p.first << ' ' << p.second << '\n';}
}
int main() {ios::sync_with_stdio(false);int t ;cin >> t;while (t--) {solve();}}G 严肃古板的秩序
思路:?只有12个,暴力,dfs3种情况,防止long long爆掉采用龟速乘
#include<bits/stdc++.h>
#pragma GCC optimize(2)
#pragma GCC optimize(3)
#pragma GCC optimize(fast)
#include<iostream>
#include<algorithm>
#include<map>
#include<set>
#include<queue>
#include<cstring>
#include<math.h>
#include<map>
#include<vector>
#include<stack>
#define ms(x,y) memset(x,y,sizeof x)
typedef long long ll;
const int maxn=2e5+10,INF = 1e18 ;
using namespace std;
int num[20],cnt = 0;
char op[3] = { '+','-','#' }, s1[20];
ll numb = 0;
bool flag = false;
ll qadd(ll a,ll b, ll p){ //龟速乘防止long long 爆掉ll res = 0;while (b){if (b & 1) res = (res + a) % p;a = (a + a) % p;b = b >> 1;}return res;
}
void dfs(ll u, ll v) {if (u == cnt - 1) {if (v == numb) flag = true;return;}if (u >= cnt) return;if (flag) return;s1[u] = op[0];dfs(u + 1, v + num[u + 2]);if (flag) return;s1[u] = op[1];dfs(u + 1, v - num[u + 2]);if (flag) return;s1[u] = op[2];if (v > 0) {dfs(u + 1, qadd(v, v, num[u + 2]));}
}void solve(){string s;cin >> s;for (int i = 0; i < s.size(); i++) {if (isdigit(s[i])) {numb =numb*10LL+s[i] - '0';}else {num[++cnt] = numb;numb = 0LL;}}dfs(0, num[1]);int cnt1 = 0;if (flag) {for (int i = 0; i < s.size(); i++) {if (s[i] != '?')cout << s[i];else {cout << s1[cnt1++];}}}else {cout << -1 << '\n';}}
signed main()
{ios::sync_with_stdio(false);solve();
}C 忽远忽近的距离
题意:构造一个n数组,使得每个2<=|ai-i|<=3;
思路1:4,5,6可构造除7外往后的所有数
n%4==1,4,5搭配;n%4==2,4,6搭配;n%4==3,4,5,6搭配
#include<bits/stdc++.h>
#pragma GCC optimize(2)
#pragma GCC optimize(3)
#pragma GCC optimize(fast)
#include<iostream>
#include<algorithm>
#include<map>
#include<set>
#include<queue>
#include<cstring>
#include<math.h>
#include<map>#include<vector>#include<stack>
#define ms(x,y) memset(x,y,sizeof x)
#define int long long
typedef long long ll;
const int maxn=2e5+10,INF = 1e18 ;
using namespace std;
int start = 1;
void fun4() {cout << start + 2<<' ' << start + 3<<' ' << start<<' ' << start + 1<<' ';start += 4;
}
void fun5() {cout << start + 3 <<' '<< start + 4 <<' ' << start <<' ' << start + 1<<' ' << start + 2 << ' ';start+=5;
}
void fun6() {cout << start + 3 << ' ' << start + 4 << ' ' << start + 5 << ' ' << start << ' ' << start + 1 << ' ' << start + 2 << ' ';start += 6;
}void solve(){int n;cin >> n;if (n <= 3 || n == 7) {cout << -1 << '\n';return;}start = 1;int x = n / 4;int y = n % 4;if (y == 0) {for (int i = 1; i <= x; i++) {fun4();}}else if (y == 1) {for (int i = 1; i <= x - 1; i++) {fun4();}fun5();}else if (y == 2) {for (int i = 1; i <= x - 1; i++) {fun4();}fun5();}else if (y == 3) {for (int i = 1; i <= x - 1; i++) {fun4();}fun5();fun6();}}
signed main()
{ios::sync_with_stdio(false);solve();
}相关文章:

题解2023.6.5
D - Factorial Divisibility 对于a[i]>x的数一定可以整除,考虑a[i]<x的数,因为(x1)*x! (x1)! 统计ai出现的次数, 把他转换为大的阶乘, 如果, 最终1到x - 1, ai的出现次数均为0则说明可以被x!整除 #pragma GCC optimize(2) #pragma GCC optimiz…...

与声音计算研究相关的挑战赛——DCASE和L3DAS
前言:在本专栏的系列博文中,我将包含声学场景识别、声音事件检测、声源位置估计等利用机器学习或深度学习技术进行研究的、基于声音信号的相关工作成为“声音计算”。 本篇博文主要介绍与声音计算相关的两个近些年持续跟进的挑战赛:DCASE和L…...

实训总结-----Scrapy爬虫
1.安装指令 pip install scrapy 2.创建 scrapy 项目 任意终端 进入到目录(用于存储我们的项目) scrapy startproject 项目名 会在目录下面 创建一个以 项目名 命名的文件夹 终端也会有提示 cd 项目名 scrapy genspider example example.com 3.运行爬虫指令 scrapy craw…...

前端开发职业规划指南:如何做好职业规划与发展
引言 前端开发是目前互联网行业中最火热的职业之一,也是非常具有发展前景的职业之一。随着互联网技术的不断更新和发展,前端开发的职业规划也在不断地发生变化。本文将从几个方面来探讨前端开发的职业规划。 一、职业发展路径 1.前端初级工程师 前端初…...
创业第一步:如何写好商业计划书
即使你的项目不需要融资,你也把标准商业计划书作为一个工具模板来应用,帮助更全面的盘点你要做的事情。 撰写一份性感的商业计划书如同造房子:第一步是科学设计,打好结构(有清晰的撰写逻辑);第…...
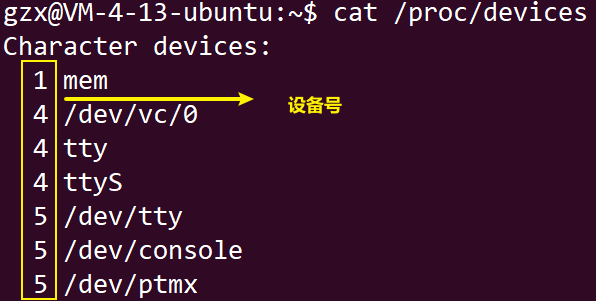
【Linux驱动】字符设备驱动相关宏 / 函数介绍(module_init、register_chrdev)
驱动运行有两种方式: 方式一:直接编译到内核,Linux内核启动时自动运行驱动程序方式二:编译成模块,使用 insmod 命令加载驱动模块 我们在调试的时候,采用第二种方式是最合适的,每次修改驱动只需…...

axios解决跨域问题
Vue3中使用axios访问聚合的天气API,出现跨域问题,需要在前端进行一些配置: 首先是修改vue.config.js: const { defineConfig } require(vue/cli-service) module.exports defineConfig({transpileDependencies: true,devServe…...

R语言作图——热图聚类及其聚类结果输出
代码 不多说了,做个记录,代码如下。 library(pheatmap) library(RColorBrewer) # args commandArgs(TRUE) betafile "twist_common_panel_434.csv" infofile "twist_common_panel_434.txt" title "twist_common_panel&qu…...

Tomcat优化
Tomcat优化 Tomcat默认安装下的缺省配置并不适合生产环境,它可能会频繁出现假死现象需要重启,只有通过不断压测优化才能让它最高效率稳定的运行。优化主要包括三方面,分别为操作系统优化(内核参数优化),Tom…...

我的GIT练习TWO
目录 前言 GIT安装教程 Git作者 GIT优点 GIT缺点 为什么要使用 Git GIT练习TWO C1 C2 C3 C4 C5 C6 C7 总结 前言 Git 是一个分布式版本控制及源代码管理工具;Git 可以为你的项目保存若干快照,以此来对整个项目进行版本管理 GIT安装教程 点击进入查看教程…...

个人器件库整理
样品本 包含如下: 电容器件: 元件值封装备注钽电容47uF 10V1206钽电容10uF 10V1206电容10uF 10% 10V0603X5R,CL10A106KP8NNNC 元件值封装备注100nF电容50V,10%0603 电阻器件: 元件值封装备注75 Ω \Omega Ω…...

javascript——内存管理
JavaScript内存管理是Web开发中的一个重要主题。正确管理内存可以提高应用程序的性能和稳定性。本文将介绍JavaScript中的内存管理概念、常见的内存泄漏问题以及一些有效的内存管理技巧。 什么是JavaScript内存管理? JavaScript具有自动内存管理机制,开…...

Qt5.15.2安卓Android项目开发环境配置
1、Qt Creator 4.11.2 官方下载:https://download.qt.io/archive/qtcreator/4.11/4.11.2/ 镜像下载:https://mirrors.cloud.tencent.com/qt/archive/qtcreator/4.11/4.11.2/ 2、Qt 5.15.2 Android 官方更新器内部下载 参考:https://blog…...
)
第四十三章 弹跳训练2(灵识扫描)
“再不脱离便会陷死在里面。”这个声音似乎来自脑海深处某个隐秘角落。 双眼一睁,灵识退去,空空的头壳兀自嗡嗡作响,一股说不清道不明的失落感笼罩全身,似要将自己拖入抑郁的谷底。 不!没什么好失落沮丧的!…...

【location对象的方法,history对象,navigator--BOM】
location对象的方法 location.assign()//跟href一样,可以跳转页面(也称重定向页面) location.replace()//替换当前页面,因为不记录历史,所以不能后退页面 location.reload()//重新加载页面,相当于刷新按钮或…...
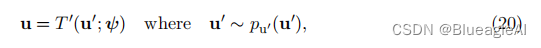
论文笔记:Normalizing Flows for Probabilistic Modeling and Inference
Abstract 正则流(Normalizing flows)提供了一种通用的机制来定义富有表达力的概率分布,只需要指定一个(通常简单的)基础分布和一系列可逆变换。 Intraduction 正则流通过将简单的密度通过一系列变换来产生更丰富、可…...

java 异常类介绍
Java 异常(Exception)是指在程序运行期间出现的错误或异常情况。Java 异常处理机制允许程序在出现异常情况时进行处理,避免程序崩溃或出现不可预知的错误 一、Java 异常的概念 Java 异常是指程序在运行期间出现的错误或异常情况。Java 异常…...
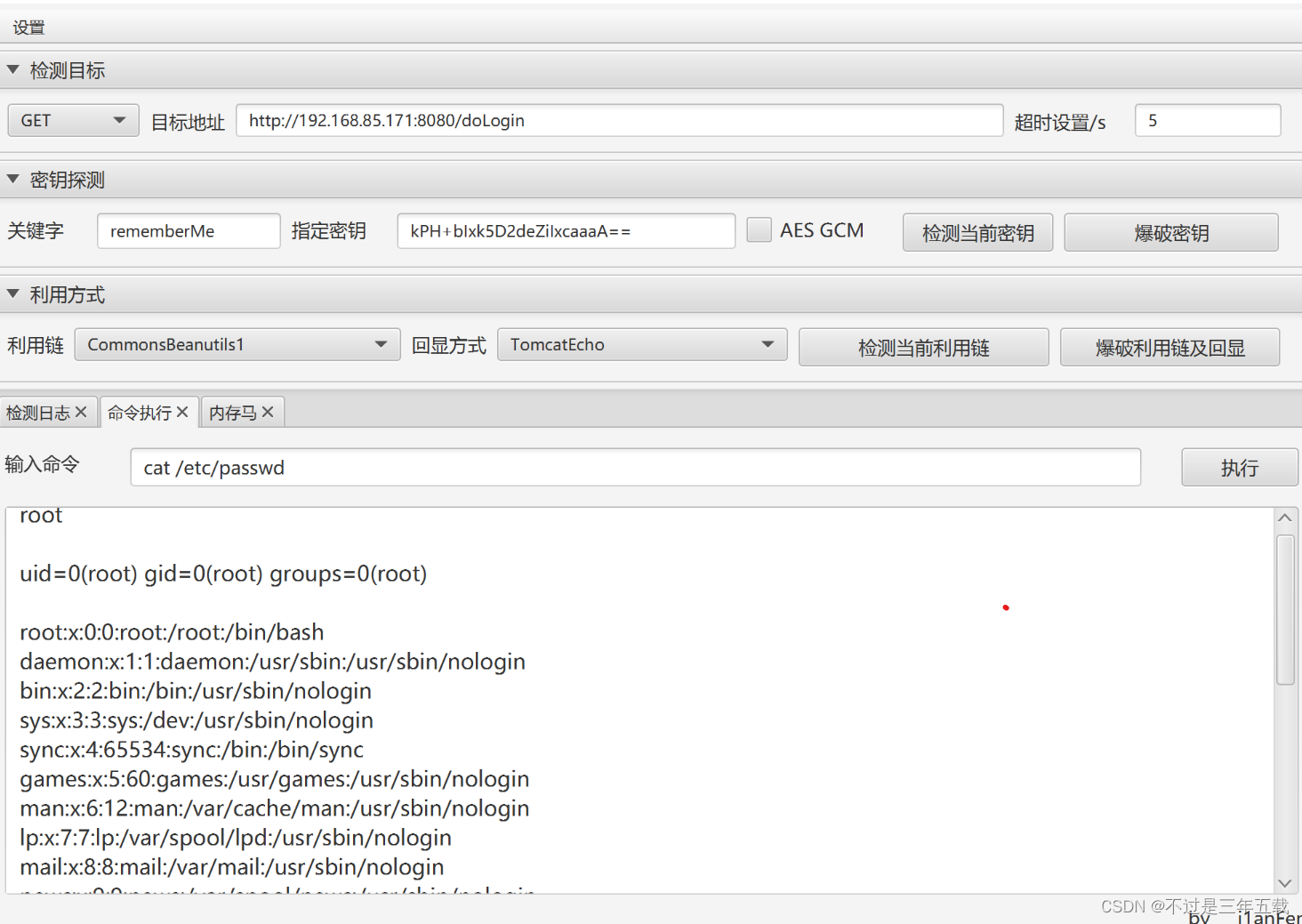
shiro 550 反序列化rce
Apach shiro 是一款开源安全框架,提供身份验证,授权,会话管理等。 shiro 550 反序列化漏洞rce 通关利用它反序列化的漏洞直接执行rce 加密的用户信息序列化后储存在名为remenber -me的cooike中。攻击者可以使用shiro默认密钥伪造cooike&am…...

【C++】---模板初阶(超详练气篇)
个人主页:平行线也会相交💪 欢迎 点赞👍 收藏✨ 留言✉ 加关注💓本文由 平行线也会相交 原创 收录于专栏【C之路】💌 本专栏旨在记录C的学习路线,望对大家有所帮助🙇 希望我们一起努力、成长&…...
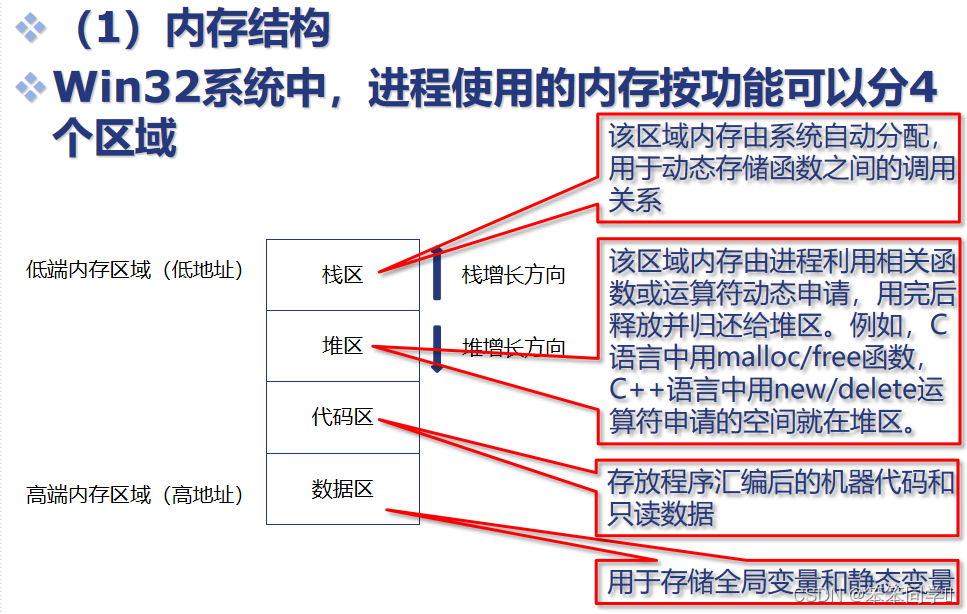
windows系统典型漏洞分析
内存结构 缓冲区溢出漏洞 缓冲区溢出漏洞就是在向缓冲区写入数据时,由于没有做边界检查,导致写入缓冲区的数据超过预先分配的边界,从而使溢出数据覆盖在合法数据上而引起系统异常的一种现象。 ESP、EPB ESP:扩展栈指针(…...

【JavaEE】-- HTTP
1. HTTP是什么? HTTP(全称为"超文本传输协议")是一种应用非常广泛的应用层协议,HTTP是基于TCP协议的一种应用层协议。 应用层协议:是计算机网络协议栈中最高层的协议,它定义了运行在不同主机上…...

Zustand 状态管理库:极简而强大的解决方案
Zustand 是一个轻量级、快速和可扩展的状态管理库,特别适合 React 应用。它以简洁的 API 和高效的性能解决了 Redux 等状态管理方案中的繁琐问题。 核心优势对比 基本使用指南 1. 创建 Store // store.js import create from zustandconst useStore create((set)…...

CentOS下的分布式内存计算Spark环境部署
一、Spark 核心架构与应用场景 1.1 分布式计算引擎的核心优势 Spark 是基于内存的分布式计算框架,相比 MapReduce 具有以下核心优势: 内存计算:数据可常驻内存,迭代计算性能提升 10-100 倍(文档段落:3-79…...

Java - Mysql数据类型对应
Mysql数据类型java数据类型备注整型INT/INTEGERint / java.lang.Integer–BIGINTlong/java.lang.Long–––浮点型FLOATfloat/java.lang.FloatDOUBLEdouble/java.lang.Double–DECIMAL/NUMERICjava.math.BigDecimal字符串型CHARjava.lang.String固定长度字符串VARCHARjava.lang…...

转转集团旗下首家二手多品类循环仓店“超级转转”开业
6月9日,国内领先的循环经济企业转转集团旗下首家二手多品类循环仓店“超级转转”正式开业。 转转集团创始人兼CEO黄炜、转转循环时尚发起人朱珠、转转集团COO兼红布林CEO胡伟琨、王府井集团副总裁祝捷等出席了开业剪彩仪式。 据「TMT星球」了解,“超级…...

linux 下常用变更-8
1、删除普通用户 查询用户初始UID和GIDls -l /home/ ###家目录中查看UID cat /etc/group ###此文件查看GID删除用户1.编辑文件 /etc/passwd 找到对应的行,YW343:x:0:0::/home/YW343:/bin/bash 2.将标红的位置修改为用户对应初始UID和GID: YW3…...

【git】把本地更改提交远程新分支feature_g
创建并切换新分支 git checkout -b feature_g 添加并提交更改 git add . git commit -m “实现图片上传功能” 推送到远程 git push -u origin feature_g...

基于 TAPD 进行项目管理
起因 自己写了个小工具,仓库用的Github。之前在用markdown进行需求管理,现在随着功能的增加,感觉有点难以管理了,所以用TAPD这个工具进行需求、Bug管理。 操作流程 注册 TAPD,需要提供一个企业名新建一个项目&#…...

python爬虫——气象数据爬取
一、导入库与全局配置 python 运行 import json import datetime import time import requests from sqlalchemy import create_engine import csv import pandas as pd作用: 引入数据解析、网络请求、时间处理、数据库操作等所需库。requests:发送 …...

pikachu靶场通关笔记19 SQL注入02-字符型注入(GET)
目录 一、SQL注入 二、字符型SQL注入 三、字符型注入与数字型注入 四、源码分析 五、渗透实战 1、渗透准备 2、SQL注入探测 (1)输入单引号 (2)万能注入语句 3、获取回显列orderby 4、获取数据库名database 5、获取表名…...
