[USACO2022-DEC-Bronze] T2 Feeding the Cows 题解
一、题目描述
Farmer John has N (1≤N≤10^5) cows, the breed of each being either a Guernsey or a Holstein. They have lined up horizontally with the cows occupying positions labeled from 1…N.
Farmer John 有 N(1≤N≤105)头奶牛,每头奶牛的品种是更赛牛(Guernsey)或荷斯坦牛(Holstein)之一。她们沿水平方向排成一行,奶牛们占据的位置编号为 1…N。
Since all the cows are hungry, FJ decides to plant grassy patches on some of the positions 1…N. Guernseys and Holsteins prefer different types of grass, so if Farmer John decides to plant grass at some location, he must choose to planting either Guernsey-preferred grass or Holstein-preferred grass --- he cannot plant both at the same location. Each patch of grass planted can feed an unlimited number of cows of the appropriate breed.
由于奶牛们都饿了,FJ 决定在 1…N 中的某些位置上种植草地。更赛牛和荷斯坦牛喜欢不同类型的草,所以如果 Farmer John 决定在某个位置种草,他必须选择种植更赛牛喜欢的草或荷斯坦牛喜欢的草——他不能在同一个位置同时种两种草。种植的每一片草地都可以喂饱数量不限的相应品种的奶牛。
Each cow is willing to move a maximum of K (0≤K≤N−1) positions to reach a patch. Find the minimum number of patches needed to feed all the cows. Also, print a configuration of patches that uses the minimum amount of patches needed to feed the cows. Any configuration that satisfies the above conditions will be considered correct.
每头奶牛愿意移动至多 K(0≤K≤N−1)个位置以前往一个草地。求出喂饱所有奶牛所需种植的最小草地数量。此外,输出一种使用最小草地数量喂饱所有奶牛的种植方案。任何满足上述条件的方案均视为正确。
输入
INPUT FORMAT (input arrives from the terminal / stdin):
Each input contains T test cases, each describing an arrangement of cows. The first line of input contains T (1≤T≤10). Each of the T test cases follow.
每个测试用例包含 T 个子测试用例,为一种奶牛的排列。输入的第一行包含 T(1≤T≤10)。以下是 T 个子测试用例。
Each test case starts with a line containing N and K. The next line will contain a string of length N, where each character denotes the breed of the ith cow (G meaning Guernsey and H meaning Holstein).
每个子测试用例的第一行包含 N 和 K。第二行包含一个长度为 N 的字符串,其中第 i 个字符表示第 i 头奶牛的品种(G 表示更赛牛,H 表示荷斯坦牛)。
输出
OUTPUT FORMAT (print output to the terminal / stdout):
For each of the T test cases, please write two lines of output. For the first line, print the minimum number of patches needed to feed the cows. For the second line, print a string of length N that describes a configuration that feeds all the cows with the minimum number of patches. The ith character, describing the ith position, should be a '.' if there is no patch, a 'G' if there is a patch that feeds Guernseys, and a 'H' if it feeds Holsteins. Any valid configuration will be accepted.
对于 T 个子测试用例中的每一个,输出两行。第一行输出喂饱所有奶牛所需的最小草地数量。第二行输出一个长度为 N 的字符串,表示一种使用最小草地数量喂饱所有奶牛的种植方案。第 i 个字符表示第 i 个位置,若不种草则为 '.',若种植喂饱更赛牛的草则为 'G',若种植喂饱荷斯坦牛的草则为 'H'。任何合法的方案均可通过。
样例
输入
复制
6
5 0
GHHGG
5 1
GHHGG
5 2
GHHGG
5 3
GHHGG
5 4
GHHGG
2 1
GH
输出
复制
5
GHHGG
3
.GH.G
2
..GH.
2
...GH
2
...HG
2
HG
说明
Note that for some test cases, there are multiple acceptable configurations that manage to feed all cows while using the minimum number of patches. For example, in the fourth test case, another acceptable answer would be:
.GH..
注意对于某些子测试用例,存在多种可通过的方案使用最小数量的草地。例如,在第四个子测试用例中,以下是另一个可以通过的答案:
.GH..
This corresponds to placing a patch feeding Guernseys on the 2nd position and a patch feeding Holsteins on the third position. This uses the optimal number of patches and ensures that all cows are within 3 positions of a patch they prefer.
这个方案在第二个位置种植一块喂饱更赛牛的草地以及在第三个位置种植一块喂饱荷斯坦牛的草地。这使用了最小数量的草地并确保了所有奶牛都在她们喜欢的草地的 3 个位置以内。
SCORING:
Inputs 2 through 4 have N≤10.
Inputs 5 through 8 have N≤40.
Inputs 9 through 12 have N≤10^5.
测试点性质:
测试点 2-4 满足 N≤10。
测试点 5-8 满足 N≤40。
测试点 9-12 满足 N≤10^5。
二、分析
定义放G草和H草的位置,如果牛的位置为i,草的位置可以覆盖到牛的话,就不用种草,否则要种草。
草要尽量往右重,尽可能少地种草。
如果当前没有种草,直接种草即可,否则再往前找种草的位置。
例1:
rightH | 1 | 2 | 3 | 4 | 5 | |
5,1 | G | H | H | G | G | |
rightG | ||||||
i=1 | . | G | . | . | . | i=1的G可以吃到i+k的草,rightG更新为种草的位置,这个草还可以覆盖到rightG+k位置 |
rightG |
例2:
2,1 | G | H | ||||
i=1 | . | G | i=1的G可以吃到i+k的草,rightG更新为种草的位置,这个草还可以覆盖到rightG+k位置 | |||
i=2 | i=2的H可以吃到i+k的草,i+k>n,所以最大种草位置为n,但是此位置已经有草了,往前找位置种草 |
三、代码
#include <bits/stdc++.h>
using namespace std;
const int N=1e5+5;
char cow[N],ans[N];
int main() {int t; cin >> t;while (t--){memset(ans,'.',sizeof(ans));int ansCnt=0,rightH=0,rightG=0;int n,k;cin>>n>>k;for(int i=1;i<=n;i++){cin>>cow[i];if(cow[i]=='H'){if(i<=rightH)continue; //rightH可以覆盖这个H牛for(int j=min(n,i+k);j>=max(1,i-k);j--){//找到尽量右边的位置进行种草[i-k,i+k]为可以覆盖此奶牛的种草位置if(ans[j]=='.'){ans[j]='H';ansCnt++;rightH=j+k;//更新草的位置break;}}}else{if(i<=rightG)continue;for(int j=min(n,i+k);j>=max(1,i-k);j--){if(ans[j]=='.'){ans[j]='G';ansCnt++;rightG=j+k;break;}}}}cout<<ansCnt<<endl;for(int i=1;i<=n;i++){cout<<ans[i];}cout<<endl;}return 0;
}相关文章:

[USACO2022-DEC-Bronze] T2 Feeding the Cows 题解
一、题目描述Farmer John has N (1≤N≤10^5) cows, the breed of each being either a Guernsey or a Holstein. They have lined up horizontally with the cows occupying positions labeled from 1…N.Farmer John 有 N(1≤N≤105)头奶牛,…...

Unity法线贴图原理理解(为什么存在切线空间?存的值是什么?)
Unity法线贴图原理理解(为什么存在切线空间?存的值是什么?)写在前面1、为什么用法线贴图?2、用什么存法线?3、法线向量为什么存在切线空间?法线贴图存得是什么?4、法线贴图为什么会偏蓝…...
【JavaWeb】传输层协议——UDP + TCP
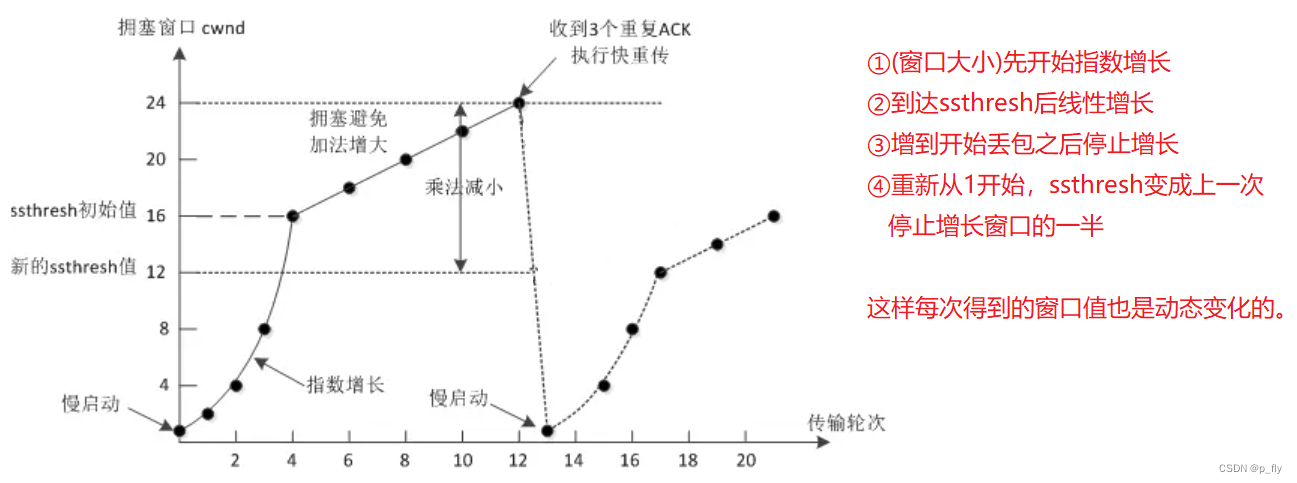
目录 UDP协议 UDP协议结构 UDP的特点 TCP协议 TCP协议结构 TCP的特点 TCP的十个核心机制 确认应答 超时重传 连接管理 滑动窗口 流量控制 阻塞控制 延迟应答 捎带应答 粘包问题 异常处理 UDP协议 UDP协议结构 源端口:存储的是发送方的端口号。 目的…...

C++ 中是用来修饰:内置类型变量、自定义对象、成员函数、返回值、函数参数
const 是 constant 的缩写,本意是不变的,不易改变的意思。在 C 中是用来修饰内置类型变量,自定义对象,成员函数,返回值,函数参数。 一. const修饰 普通类型的变量 const int a 7; int b a; // 正确 …...

av 146 002
61. 一个新的敏捷项目经理正试图确定团队该如何执行一个发布计划的进度。哪种工具可以更深入地了解团队的进展? A. 发布计划系统 B. 产品路线图。 C. 看板。 D. 燃尽图 62. 你的项目发起人找到你,让你知道他正在考虑给你项目中的一位高级工程师颁发1000美元的现…...

小红书用户画像 | 小红书数据平台
小红书的用户画像是小红书品牌营销的必备技能,也是小红书推广种草的一个重要前提。通过对小红书用户画像进行分析,对品牌进行精准营销,实现更高的流量转化。 2022小红书粉丝人群画像 千瓜数据在2022年发布的千瓜活跃用户画像趋势报告中分析了…...
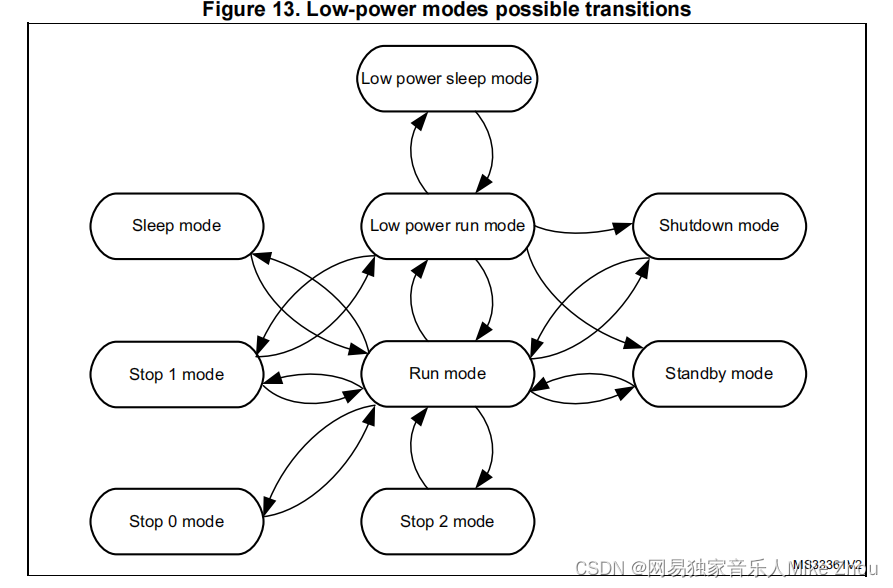
【STM32笔记】低功耗模式下GPIO、外设、时钟省电配置避坑
【STM32笔记】低功耗模式下GPIO、外设、时钟省电配置避坑 前文: blog.csdn.net/weixin_53403301/article/details/128216064 【STM32笔记】HAL库低功耗模式配置(ADC唤醒无法使用、低功耗模式无法烧录解决方案) blog.csdn.net/weixin_534033…...

Linux内存分区(swap)
目录 1、使用物理分区创建内存交换分区 2、使用文件创建内存交换文件 当硬件的设备资源充足的话,那么swap是不会被我们的系统所使用到的,所以swap会被利用到的时刻通常就是物理内存不足的情况 我们知道CPU所读取的数据都来自于内存,那么当…...

第六章——抽样分布
文章目录1、统计量的定义2、常用的统计量3、经验分布函数4、正态总体常用统计量的分布4.1、卡方分布4.1.1、卡方分布的定义4.1.2、卡方分布的性质4.2、t分布4.2.1、t分布的定义4.2.2、t分布的性质4.3、F分布4.3.1、F分布的定义4.3.2、F分布的性质5、正态总体的样本均值与样本方…...
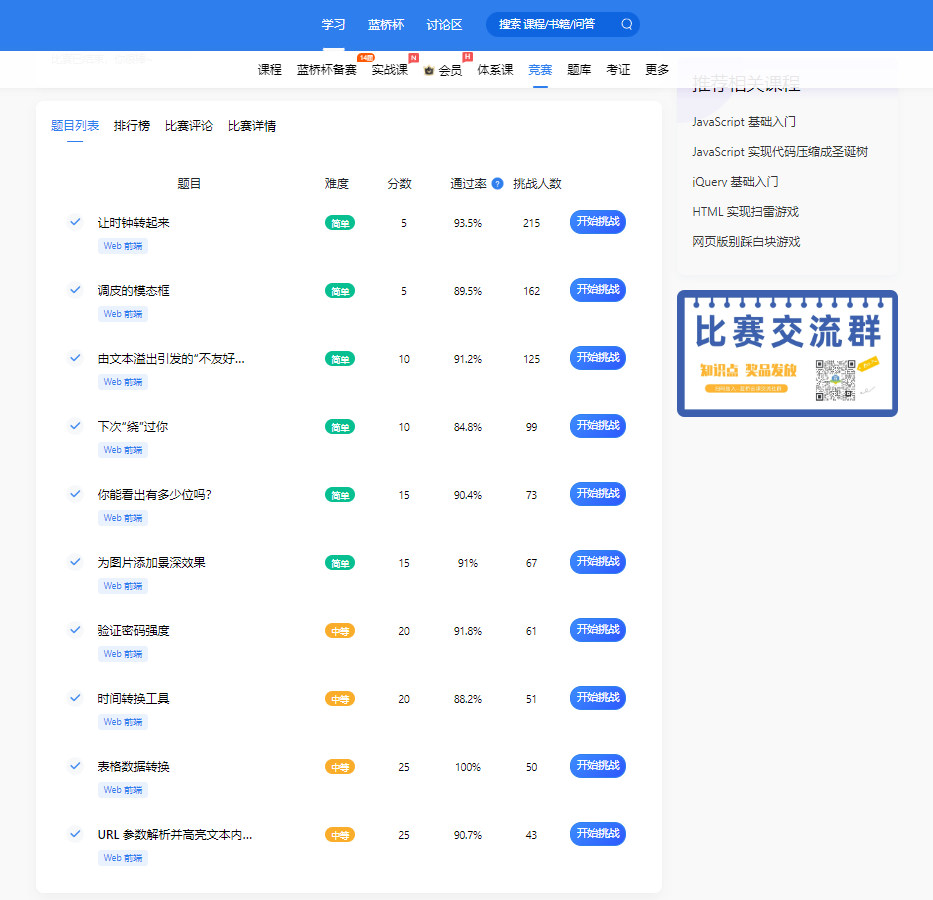
蓝桥云课-声网编程赛(声网编程竞赛7月专场)题解
比赛题目快速链接:https://www.lanqiao.cn/contests/lqENT02/challenges/ 让时钟转起来(考点:css:transform) // index.js function main() {// 题解前理解一个东西:// 时针每过一小时,转30 原…...
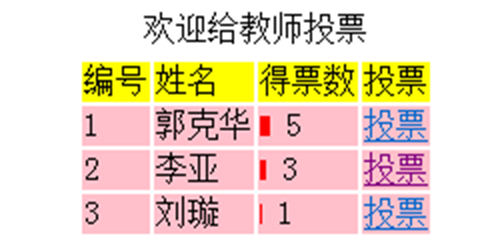
Java高手速成 | Java web 实训之投票系统
01、投票系统的案例需求 在本篇中,我们将制作一个投票系统,让学生给自己喜爱的老师投票。该系统由1个界面组成,系统运行,出现投票界面,如图所示: ▍显示效果 在这个界面中,标题为:“欢迎给教师投票”;在界面上有一个表格,显示了各位教师的编号、姓名、得票数;其中…...

排序的基本概念
按数据存储介质:内部排序和外部排序按比较器个数:串行排序和并行排序按主要操作:比较排序和基数排序插入排序:基本思想:每步将一个待排序的对象,按其关键码大小,插入到前面已经排好序的一组对象…...

面试笔试资料--Java
这里写自定义目录标题1.同步和异步有何异同?在什么情况下分别使用他们?举例说明1.同步和异步有何异同?在什么情况下分别使用他们?举例说明 1.1概念 Java中交互方式分为同步和异步两种: 同步交互:指发送…...

基于TC377的MACL-ADC General配置解读
目录标题一、MACL-ADC General1.Config Variant与AdcConfigSet2. AdcGeneral3.AdcPublishedInformation二、最终对应达芬奇生成内容一、MACL-ADC General 1.Config Variant与AdcConfigSet Config Variant :变体配置,默认选择VariantPostBuild就好了&…...

error: src refspec master does not match any.处理方案
问题描述 在使用git bash指令将项目上传到github时,总是遇到一些错误无法解决。 下面是我遇到的一个问题 error: src refspec master does not match any. error: failed to push some refs to XXXX.git 原因分析: 错误:SRC ReFSPEC主控器不…...

防火墙有关iptables的知识点
基本概念 什么是防火墙 在计算中,防火墙是基于预定安全规则来监视和控制传入和传出网络流量的网络安全系统。该计算机流入流出的所有网络通信均要经过此防火墙。防火墙对流经它的网络通信进行扫描,这样能够过滤掉一些攻击,以免其在目标计算机…...

路肩石水渠机在施工公路项目中工艺特点的匹配
新建公路路肩项目在目前公路项目中的技术手段和实现方式,大多数依靠机械设备来机械来进行,还有一部分通过人工传统的预制作业和安装模式来进行,两种工艺特点的对比来说对于补充完善建设手段和效果实现有很重要的意义. 其中采用了机械设备进行一次成型制作的过程,按照设计需求匹…...

JS 动态爱心(HTML+CSS+JS)
✅作者简介:2022年博客新星 第八。热爱国学的Java后端开发者,修心和技术同步精进。 🍎个人主页:Java Fans的博客 🍊个人信条:不迁怒,不贰过。小知识,大智慧。 💞当前专栏…...
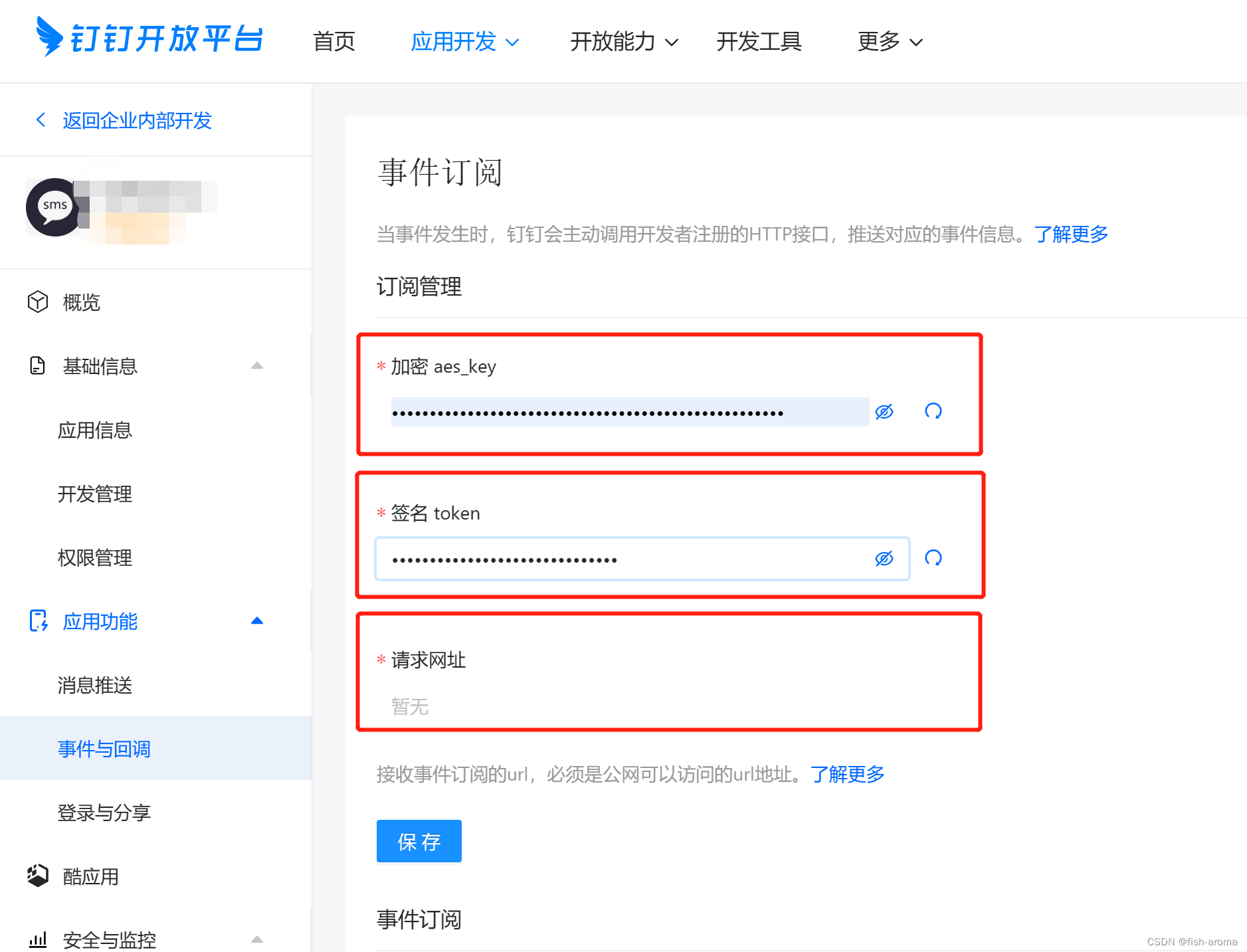
钉钉配置事件订阅(Python)
钉钉配置事件订阅 0.需求分析 需要实现钉钉企业通讯录同步至企业微信通讯录,这就需要用到钉钉的事件与回调 1.配置应用 登陆开放平台 https://open-dev.dingtalk.com/去企业内部开发里面,先创建个应用,后面都借用这个应用来调接口 创建完…...

Linux-Udev机制
一:Udev概述 udev 是一个用户空间的设备管理器,用于为事件设置处理程序。作为守护进程, udev 接收的事件主要由 linux 内核生成,这些事件是外部设备产生的物理事件。总之, udev 探测外设和热插拔,将设备控制权传递给内核,例如加载内核模块或设备固件。udev 是一个用户空…...

Unity3D中Gfx.WaitForPresent优化方案
前言 在Unity中,Gfx.WaitForPresent占用CPU过高通常表示主线程在等待GPU完成渲染(即CPU被阻塞),这表明存在GPU瓶颈或垂直同步/帧率设置问题。以下是系统的优化方案: 对惹,这里有一个游戏开发交流小组&…...

从零实现富文本编辑器#5-编辑器选区模型的状态结构表达
先前我们总结了浏览器选区模型的交互策略,并且实现了基本的选区操作,还调研了自绘选区的实现。那么相对的,我们还需要设计编辑器的选区表达,也可以称为模型选区。编辑器中应用变更时的操作范围,就是以模型选区为基准来…...

23-Oracle 23 ai 区块链表(Blockchain Table)
小伙伴有没有在金融强合规的领域中遇见,必须要保持数据不可变,管理员都无法修改和留痕的要求。比如医疗的电子病历中,影像检查检验结果不可篡改行的,药品追溯过程中数据只可插入无法删除的特性需求;登录日志、修改日志…...

多场景 OkHttpClient 管理器 - Android 网络通信解决方案
下面是一个完整的 Android 实现,展示如何创建和管理多个 OkHttpClient 实例,分别用于长连接、普通 HTTP 请求和文件下载场景。 <?xml version"1.0" encoding"utf-8"?> <LinearLayout xmlns:android"http://schemas…...

PPT|230页| 制造集团企业供应链端到端的数字化解决方案:从需求到结算的全链路业务闭环构建
制造业采购供应链管理是企业运营的核心环节,供应链协同管理在供应链上下游企业之间建立紧密的合作关系,通过信息共享、资源整合、业务协同等方式,实现供应链的全面管理和优化,提高供应链的效率和透明度,降低供应链的成…...

LeetCode - 394. 字符串解码
题目 394. 字符串解码 - 力扣(LeetCode) 思路 使用两个栈:一个存储重复次数,一个存储字符串 遍历输入字符串: 数字处理:遇到数字时,累积计算重复次数左括号处理:保存当前状态&a…...

【磁盘】每天掌握一个Linux命令 - iostat
目录 【磁盘】每天掌握一个Linux命令 - iostat工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景 注意事项 【磁盘】每天掌握一个Linux命令 - iostat 工具概述 iostat(I/O Statistics)是Linux系统下用于监视系统输入输出设备和CPU使…...
)
python爬虫:Newspaper3k 的详细使用(好用的新闻网站文章抓取和解析的Python库)
更多内容请见: 爬虫和逆向教程-专栏介绍和目录 文章目录 一、Newspaper3k 概述1.1 Newspaper3k 介绍1.2 主要功能1.3 典型应用场景1.4 安装二、基本用法2.2 提取单篇文章的内容2.2 处理多篇文档三、高级选项3.1 自定义配置3.2 分析文章情感四、实战案例4.1 构建新闻摘要聚合器…...

什么是EULA和DPA
文章目录 EULA(End User License Agreement)DPA(Data Protection Agreement)一、定义与背景二、核心内容三、法律效力与责任四、实际应用与意义 EULA(End User License Agreement) 定义: EULA即…...

uniapp中使用aixos 报错
问题: 在uniapp中使用aixos,运行后报如下错误: AxiosError: There is no suitable adapter to dispatch the request since : - adapter xhr is not supported by the environment - adapter http is not available in the build 解决方案&…...
