群的定义及性质
群的定义
设 < G , ⋅ > \left<G,\cdot\right> ⟨G,⋅⟩为独异点,若 G G G中每个元素关于 ⋅ \cdot ⋅都是可逆的,则称 < G , ⋅ > \left<G,\cdot\right> ⟨G,⋅⟩为群
由于群中结合律成立,每个元素的逆元是唯一的
若群 < G , ⋅ > \left<G,\cdot\right> ⟨G,⋅⟩中的二元运算 ⋅ \cdot ⋅是可交换的,则称 < G , ⋅ > \left<G,\cdot\right> ⟨G,⋅⟩为可交换群,也称阿贝尔群
群的判定
定理1:设 < G , ⋅ > \left<G, \cdot\right> ⟨G,⋅⟩为半群,若
(1)有左单位元,即 ∃ e l ∈ G \exists e_l\in G ∃el∈G使 ∀ a ∈ G , e l ⋅ a = a \forall a \in G, e_l \cdot a = a ∀a∈G,el⋅a=a
(2)每个元素有左逆元,即 ∀ a ∈ G , ∃ a l ∈ G \forall a \in G, \exists a_l \in G ∀a∈G,∃al∈G,使 a l ⋅ a = e l a_l \cdot a=e_l al⋅a=el则 < G , ⋅ > \left<G, \cdot \right> ⟨G,⋅⟩是群
证明:因为 a l ∈ G a_l \in G al∈G,所以 ∃ a ′ ⋅ a l = e l \exists a^{\prime} \cdot a_l = e_l ∃a′⋅al=el,于是
a ⋅ a l = e l ⋅ ( a ⋅ a l ) = ( a ′ ⋅ a l ) ⋅ ( a ⋅ a l ) = a ′ ⋅ ( a l ⋅ a ) ⋅ a l = a ′ ⋅ e l ⋅ a l = a ′ ⋅ ( e l ⋅ a l ) = a ′ ⋅ a l = e l \begin{aligned} a \cdot a_l &=e_l\cdot \left(a \cdot a_l\right)\\ &=\left(a^{\prime} \cdot a_l \right) \cdot \left(a \cdot a_l\right)\\ &=a^{\prime} \cdot \left(a_l\cdot a\right)\cdot a_l\\ &=a^{\prime} \cdot e_l \cdot a_l \\ &=a^{\prime}\cdot\left(e_l\cdot a_l\right)\\ &=a^{\prime} \cdot a_l\\ &=e_l \end{aligned} a⋅al=el⋅(a⋅al)=(a′⋅al)⋅(a⋅al)=a′⋅(al⋅a)⋅al=a′⋅el⋅al=a′⋅(el⋅al)=a′⋅al=el
因此 a l a_l al也是 a a a的右逆元,进而 a a a可逆
∀ a ∈ G \forall a \in G ∀a∈G
a ⋅ e l = a ⋅ ( a l ⋅ a ) = ( a ⋅ a l ) ⋅ a = e l ⋅ a = a a\cdot e_l = a\cdot\left(a_l\cdot a\right) = \left(a\cdot a_l\right) \cdot a = e_l \cdot a = a a⋅el=a⋅(al⋅a)=(a⋅al)⋅a=el⋅a=a
因此 e l e_l el是单位元
因此 < G , ⋅ > \left<G,\cdot\right> ⟨G,⋅⟩是群
将本定理中的左同时改成右也成立,但是一左一右不一定
定理2:设 < G , ⋅ > \left<G, \cdot\right> ⟨G,⋅⟩是半群,若 ∀ a , b ∈ G \forall a,b\in G ∀a,b∈G,方程 a ⋅ x = b a\cdot x=b a⋅x=b和 y ⋅ a = b y\cdot a=b y⋅a=b在 G G G中都有接,则 < G , ⋅ > \left<G,\cdot \right> ⟨G,⋅⟩是群
证明:
(1)取 a ∈ G a\in G a∈G设 e l e_l el为 y ⋅ a = a y\cdot a=a y⋅a=a的一个解, ∀ b ∈ G \forall b \in G ∀b∈G,令 c c c为 a ⋅ x = b a\cdot x=b a⋅x=b的一个解,则
e l ⋅ b = e l ⋅ ( a ⋅ c ) = ( e l ⋅ a ) ⋅ c = a ⋅ c = b e_l \cdot b = e_l\cdot \left(a\cdot c\right)=\left(e_l\cdot a\right) \cdot c = a\cdot c = b el⋅b=el⋅(a⋅c)=(el⋅a)⋅c=a⋅c=b
故 e l e_l el是左单位元
(2) ∀ a ∈ G \forall a \in G ∀a∈G,令 a l a_l al为 y ⋅ a = e l y\cdot a = e_l y⋅a=el的一个解,则 a l ⋅ a = e l a_l\cdot a = e_l al⋅a=el
由定理1, < G , ⋅ > \left<G,\cdot \right> ⟨G,⋅⟩是群
定理3:设 < G , ⋅ > \left<G, \cdot\right> ⟨G,⋅⟩是有限半群,若 G G G中消去律成立,则 < G , ⋅ > \left<G,\cdot\right> ⟨G,⋅⟩是群
证明:
设 G = { a 1 , a 2 , ⋯ , a n } G = \left\{a_1,a_2,\cdots, a_n\right\} G={a1,a2,⋯,an}
∀ a , b ∈ G \forall a,b \in G ∀a,b∈G
作 G ′ = { a ⋅ a 1 , a ⋅ a 2 , ⋯ , a ⋅ a n } G^{\prime} = \left\{a\cdot a_1, a\cdot a_2,\cdots, a\cdot a_n\right\} G′={a⋅a1,a⋅a2,⋯,a⋅an}, G ′ ⊆ G G^{\prime} \subseteq G G′⊆G
因为消去律成立,若 i ≠ j i \neq j i=j,则 a ⋅ a i ≠ a ⋅ a j a\cdot a_i \neq a \cdot a_j a⋅ai=a⋅aj
因此 ∣ G ′ ∣ = G \left|G^{\prime} \right| = G ∣G′∣=G,则 G ′ = G G^{\prime} = G G′=G
因为 b ∈ G b \in G b∈G,有 b ∈ G p r i m e b\in G^{prime} b∈Gprime
即 ∃ k ∈ N \exists k \in \mathbb{N} ∃k∈N,使得 a ⋅ a k = b a\cdot a_k=b a⋅ak=b,所以 a k ∈ G a_k \in G ak∈G是方程 a ⋅ x = b a\cdot x=b a⋅x=b的解
同理, ∀ a , b ∈ G \forall a,b\in G ∀a,b∈G, y ⋅ a = b y\cdot a=b y⋅a=b在 G G G中有解
由定理2, < G , ⋅ > \left<G,\cdot \right> ⟨G,⋅⟩是群
群的性质
设 < G , ⋅ > \left<G, \cdot\right> ⟨G,⋅⟩是群,则
(1) ∀ a , b ∈ G , ( a ⋅ b ) − 1 = b − 1 ⋅ a − 1 \forall a,b \in G, \left(a\cdot b\right)^{-1} = b^{-1}\cdot a^{-1} ∀a,b∈G,(a⋅b)−1=b−1⋅a−1;
(2) ∀ a , b ∈ G \forall a,b\in G ∀a,b∈G,方程 a ⋅ x = b a\cdot x=b a⋅x=b和 y ⋅ a = b y\cdot a=b y⋅a=b在 G G G中有唯一解;
(3) G G G中消去律成立
证明:
(1)
因为 ( b − 1 ⋅ a − 1 ) ⋅ ( a ⋅ b ) = e \left(b^{-1}\cdot a^{-1}\right) \cdot \left(a\cdot b\right) = e (b−1⋅a−1)⋅(a⋅b)=e
并且 ( a ⋅ b ) ⋅ ( b − 1 ⋅ a − 1 ) = e \left(a\cdot b\right)\cdot \left(b^{-1}\cdot a^{-1}\right) = e (a⋅b)⋅(b−1⋅a−1)=e
所以 ( a ⋅ b ) − 1 = b − 1 ⋅ a − 1 \left(a\cdot b\right)^{-1} = b^{-1}\cdot a^{-1} (a⋅b)−1=b−1⋅a−1
(2) a ⋅ ( a − 1 ⋅ b ) = b a\cdot\left(a^{-1}\cdot b\right) = b a⋅(a−1⋅b)=b所以 a − 1 ⋅ b a^{-1}\cdot b a−1⋅b是方程 a ⋅ x = b a\cdot x=b a⋅x=b在 G G G中的解
若 c c c也是 a ⋅ x = b a\cdot x = b a⋅x=b在 G G G中的解,即 a ⋅ c = b a\cdot c = b a⋅c=b,则
c = e ⋅ c = ( a − 1 ⋅ a ) ⋅ c = a − 1 ⋅ ( a ⋅ c ) = a − 1 ⋅ b c = e\cdot c = \left(a^{-1}\cdot a\right)\cdot c=a^{-1}\cdot \left(a\cdot c\right) = a^{-1}\cdot b c=e⋅c=(a−1⋅a)⋅c=a−1⋅(a⋅c)=a−1⋅b
同理 y ⋅ a = b y\cdot a = b y⋅a=b在 G G G中由唯一解
(3) G G G中每个元素都是可逆的,又因为可逆元都是可约元,故 G G G中消去律成立
元素的阶
设 < G , ⋅ > \left<G,\cdot\right> ⟨G,⋅⟩是群, a ∈ G a\in G a∈G, a a a的整数次幂可归纳定义为:
(1) a 0 = e a^{0}=e a0=e
(2) a n + 1 = a n ⋅ a , n ∈ N a^{n+1}=a^{n} \cdot a, n\in \mathbb{N} an+1=an⋅a,n∈N
(3) a − n = ( a − 1 ) n , n ∈ I + a^{-n} = \left(a^{-1}\right)^{n} , n\in \mathbb{I}_+ a−n=(a−1)n,n∈I+
容易证明 ∀ m , n ∈ I , a m ⋅ a n = a m + n , ( a m ) n = a m n \forall m,n\in\mathbb{I}, a^{m}\cdot a^n=a^{m+n},\left(a^m\right)^n=a^{mn} ∀m,n∈I,am⋅an=am+n,(am)n=amn
定义:设 < G , ⋅ > \left<G,\cdot\right> ⟨G,⋅⟩是群, a ∈ G a\in G a∈G,若 ∀ n ∈ I \forall n \in \mathbb{I} ∀n∈I, a n ≠ e a^{n}\neq e an=e则称 a a a的阶是无限的;
否则称使 a n = e a^{n}=e an=e的最小正整数 n n n为 a a a的阶
a a a的阶也称 a a a的周期,常用 ∣ a ∣ \left|a\right| ∣a∣表示
显然单位元使群中阶为 1 1 1的唯一元素
定理1:设 < G , ⋅ > \left<G,\cdot\right> ⟨G,⋅⟩使群, a ∈ G a\in G a∈G,且 ∣ a ∣ = n \left|a\right| = n ∣a∣=n,则 a k = e a^k = e ak=e当且仅当 n ∣ k n\mid k n∣k
证明:
充分性:若 n ∣ k n\mid k n∣k,则 ∃ q ∈ I \exists q\in \mathbb{I} ∃q∈I,使 k = q n k=qn k=qn,则
a k = a q n = ( a n ) q = e q = e a^k =a^{qn} = \left(a^n\right) ^q = e^q =e ak=aqn=(an)q=eq=e
必要性:若 a k = e a^k=e ak=e,设 k = q n + r , 0 ≤ r < n k = qn + r, 0\le r < n k=qn+r,0≤r<n,则
a r = a k − q n = a k ⋅ ( a n ) − q = e ⋅ ( e ) − q = e a^r = a^{k-qn} = a^k \cdot \left(a^n\right)^{-q}=e\cdot \left(e\right)^{-q} = e ar=ak−qn=ak⋅(an)−q=e⋅(e)−q=e
但 n n n使使 a n = e a^n=e an=e的最小正整数,所以 r = 0 r=0 r=0, k = q n k=qn k=qn,故 n ∣ k n\mid k n∣k
定理2:设 < G , ⋅ > \left<G,\cdot\right> ⟨G,⋅⟩使群, a ∈ G a\in G a∈G,且 ∣ a ∣ = n , k ∈ I \left|a\right|=n, k\in \mathbb{I} ∣a∣=n,k∈I
则 ∣ a k ∣ = n ( k , n ) \left|a^k\right| = \frac{n}{\left(k,n\right)} ak =(k,n)n,特别地, ∣ a − 1 ∣ = ∣ a ∣ \left|a^{-1}\right|=\left|a\right| a−1 =∣a∣
证明:设 ∣ a k ∣ = m \left|a^k\right|=m ak =m,则 a k m = e a^{km}=e akm=e,由定理1, n ∣ k m n\mid km n∣km,所以
n ( k , n ) ∣ k ( k , n ) m \frac{n}{\left(k,n\right)}\mid \frac{k}{\left(k,n\right)}m (k,n)n∣(k,n)km
而 n ( k , n ) \frac{n}{\left(k,n\right)} (k,n)n与 k ( k , n ) \frac{k}{\left(k,n\right)} (k,n)k互质,故 n ( k , n ) ∣ m \frac{n}{\left(k,n\right)}\mid m (k,n)n∣m,又因为
( a k ) n ( k , n ) = ( a n ) k ( k , n ) = e \left(a^k\right)^{\frac{n}{\left(k,n\right)}}=\left(a^n\right)^{\frac{k}{\left(k,n\right)}}=e (ak)(k,n)n=(an)(k,n)k=e
所以 m ∣ n ( k , n ) m\mid \frac{n}{\left(k,n\right)} m∣(k,n)n,而 m , n ( k , n ) ∈ I + m,\frac{n}{\left(k,n\right)}\in \mathbb{I}_+ m,(k,n)n∈I+,故 m = n ( k , n ) m=\frac{n}{\left(k,n\right)} m=(k,n)n
定理3:设 < G , ⋅ > \left<G,\cdot\right> ⟨G,⋅⟩为有限群, ∣ G ∣ = n \left|G\right|=n ∣G∣=n,则 ∀ a ∈ G , ∣ a ∣ ≤ n \forall a\in G,\left|a\right|\le n ∀a∈G,∣a∣≤n
证明: ∀ a ∈ G , a , a 2 , ⋯ , a n + 1 \forall a\in G, a,a^2,\cdots, a^{n+1} ∀a∈G,a,a2,⋯,an+1中必有两个相同元,设为 a i = a j a^{i}=a^{j} ai=aj,其中 1 ≤ i < j ≤ n + 1 1\le i < j \le n+1 1≤i<j≤n+1,
则 a j − i = e a^{j-i}=e aj−i=e,故 ∣ a ∣ ≤ j − i ≤ n \left|a\right|\le j-i\le n ∣a∣≤j−i≤n
参考:
离散数学(刘玉珍)
相关文章:

群的定义及性质
群的定义 设 < G , ⋅ > \left<G,\cdot\right> ⟨G,⋅⟩为独异点,若 G G G中每个元素关于 ⋅ \cdot ⋅都是可逆的,则称 < G , ⋅ > \left<G,\cdot\right> ⟨G,⋅⟩为群 由于群中结合律成立,每个元素的逆元是唯一的 …...

mac电脑git clone项目时报错证书过期和权限被拒绝
mac电脑使用git clone命令克隆项目时,一开始一直提示证书过期 SSL certificate problem: certificate has expired 执行以下代码关掉验证后,解决了这个问题 找到git目录 Git\git-cmd输入命令跳转到bin目录,cd bin输入命令运行git.exe执行关…...
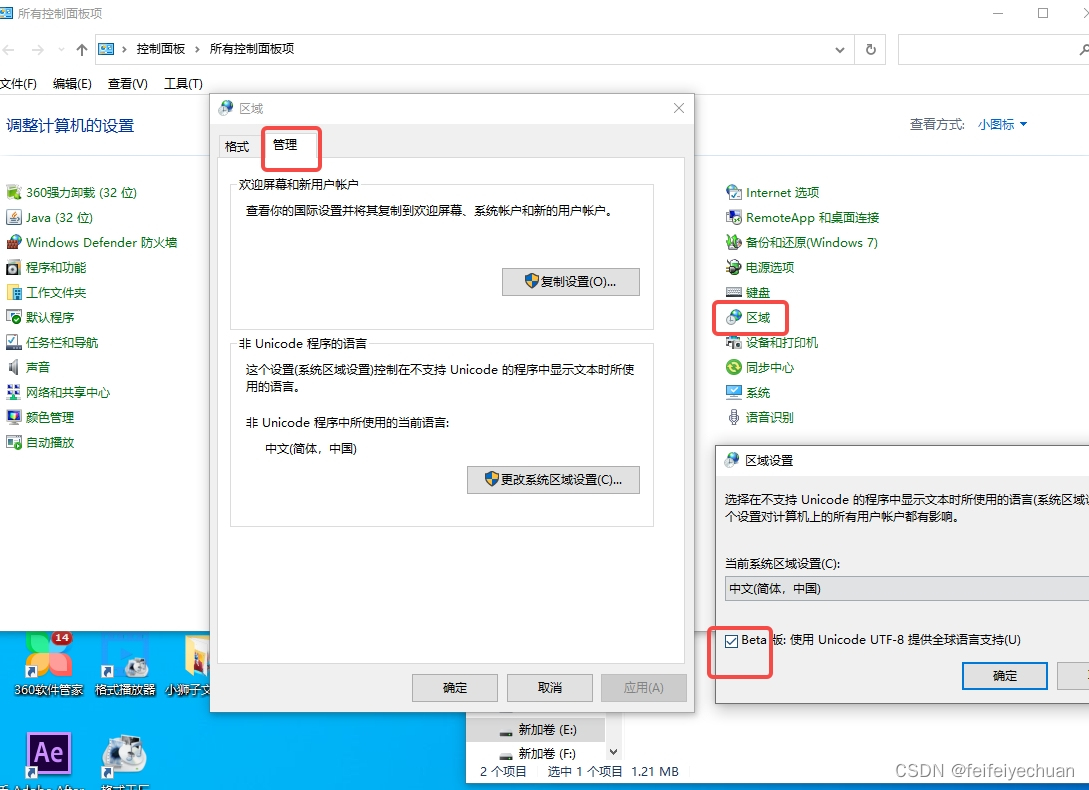
【AIGC】Photoshop AI Beta版本安装使用(永久免费)
AIGC 大爆发 Adobe近日宣布,Photoshop(测试版)应用程序发布了生成式AI绘图,这是世界上第一个创意和设计工作流程的副驾驶,为用户提供了一种神奇的新工作方式。生成式AI绘图由Adobe Firefly提供支持,Adobe的…...

01 云原生生态系统解读
云计算的技术革命 互联网时代的历程 云计算到底是什么 云计算历程 云平台的优缺点 优势 稳定性:云平台大量资源,分布式集群部署,保障服务永不宕机,几个9弹性扩展:按需索取,一键秒级开通需要的资源安全性&…...
Java——Java易错选择题复习(2)(计算机网络)
1. 下面关于源端口地址和目标端口地址的描述中,正确的是( ) A. 在TCP/UDP传输段中,源端口地址和目的端口地址是不能相同的 B. 在TCP/UDP传输段中,源端口地址和目的端口地址必须是相同的 C. 在TCP/UDP传输段中ÿ…...

【HTML5系列教程】
《HTML5系列教程》目录大纲: 介绍 内容包括HTML简介、服务器的概念、B/S、C/S软件架构、前端与后端的开发内容、HTML发展历程、浏览器内核介绍、Web标准、WebStorm工具的使用、WebStorm常用快捷键、HTML常用标签 如:文本标签(span)、排版标签(div/p/h…...
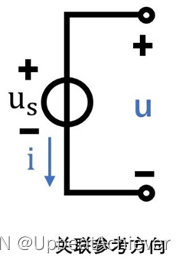
二、电压源、电流源、受控源
点我回到目录 目录 理想电压源 理想电流源 受控源 电流源做功问题 电压源做功问题 理想电压源 •定义:两端电压保持定值或一定的时间函数,且电压值与流过它的电流i无关 •特点:理想电压源两端的电压由本身决定,与外电路无关…...

骨传导是哪个意思,推荐几款性能优的骨传导耳机
骨传导耳机是通过头部骨迷路传递声音,而不是直接通过耳膜的振动来传递声音。与传统的入耳式耳机相比,骨传导耳机不会堵耳朵,在跑步、骑车等运动时可以更好的接收外界环境音,保护听力,提升安全性。此外,骨…...
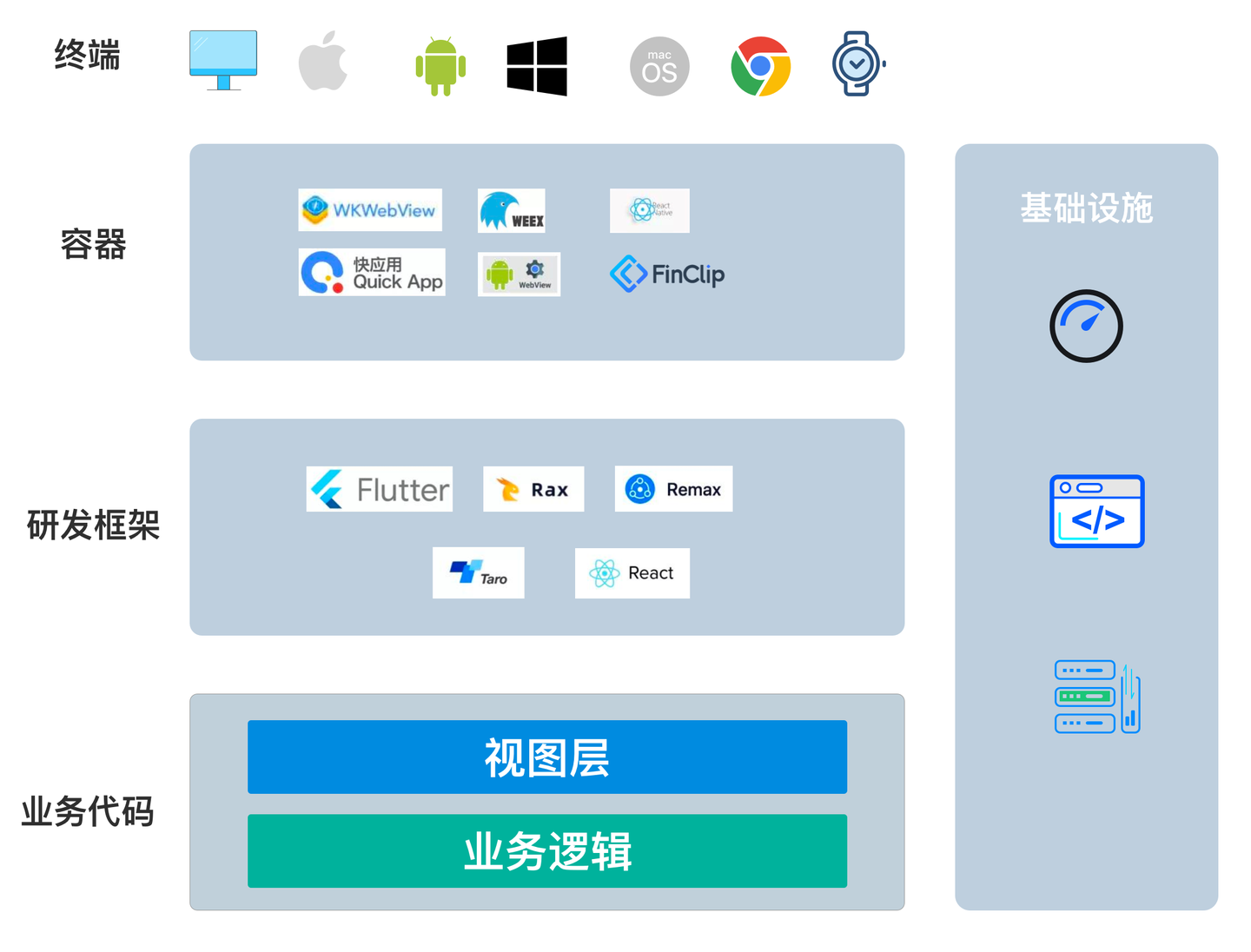
利用Taro打造灵活的移动App架构
最近公司的一些项目需要跨端框架,技术老大选了Taro,实践了一段时间下来,愈发觉得Taro是个好东西,所以在本篇文章中稍微介绍下。 什么是Taro? Taro(或称为Taro框架)是一种用于构建跨平台应用程…...
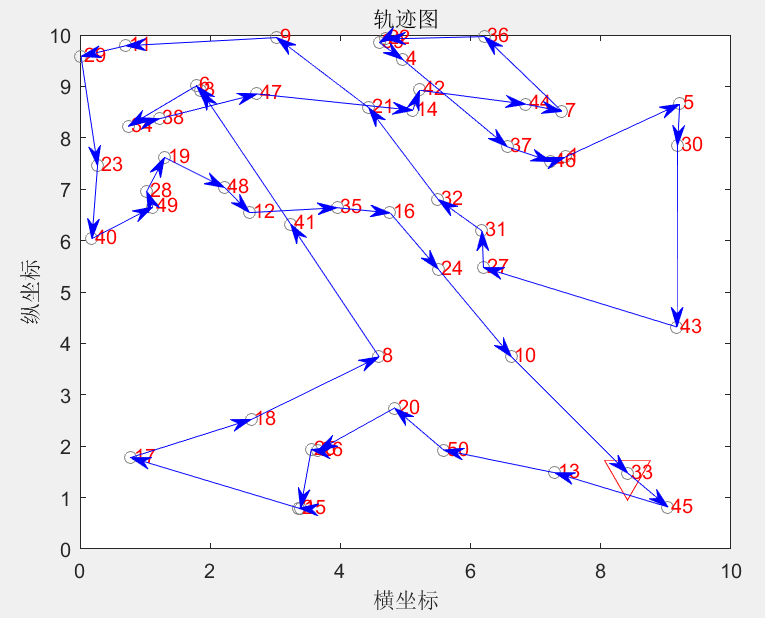
(转载)基于模拟退火算法的TSP问题求解(matlab实现)
1 理论基础 1.1 模拟退火算法基本原理 模拟退火(simulated annealing,SA)算法的思想最早是由Metropolis等提出的。其出发点是基于物理中固体物质的退火过程与一般的组合优化问题之间的相似性。模拟退火法是一种通用的优化算法,其物理退火过程由以下三部分组成&am…...

splitpcap 使用说明
背景 当PCAP原始文件特别巨大的时候,整个文件直接载入内存是相当耗时的,于是一个简单的想法是将大的PCAP切分成若干小PCAP。对于这个任务,现有工具splitcap是可以完成的。无论是按照主机对、还是按照五元组信息切分,splitcap都会…...

配置docker阿里云镜像加速
默认情况下docker安装镜像文件是从docker官方的镜像中心下载:https://hub.docker.com/ , 有时速度慢,可以通过配置docker阿里云镜像来加速,配置后,就从国内阿里云下载。 注册阿里云用户,登录->工作台-&g…...
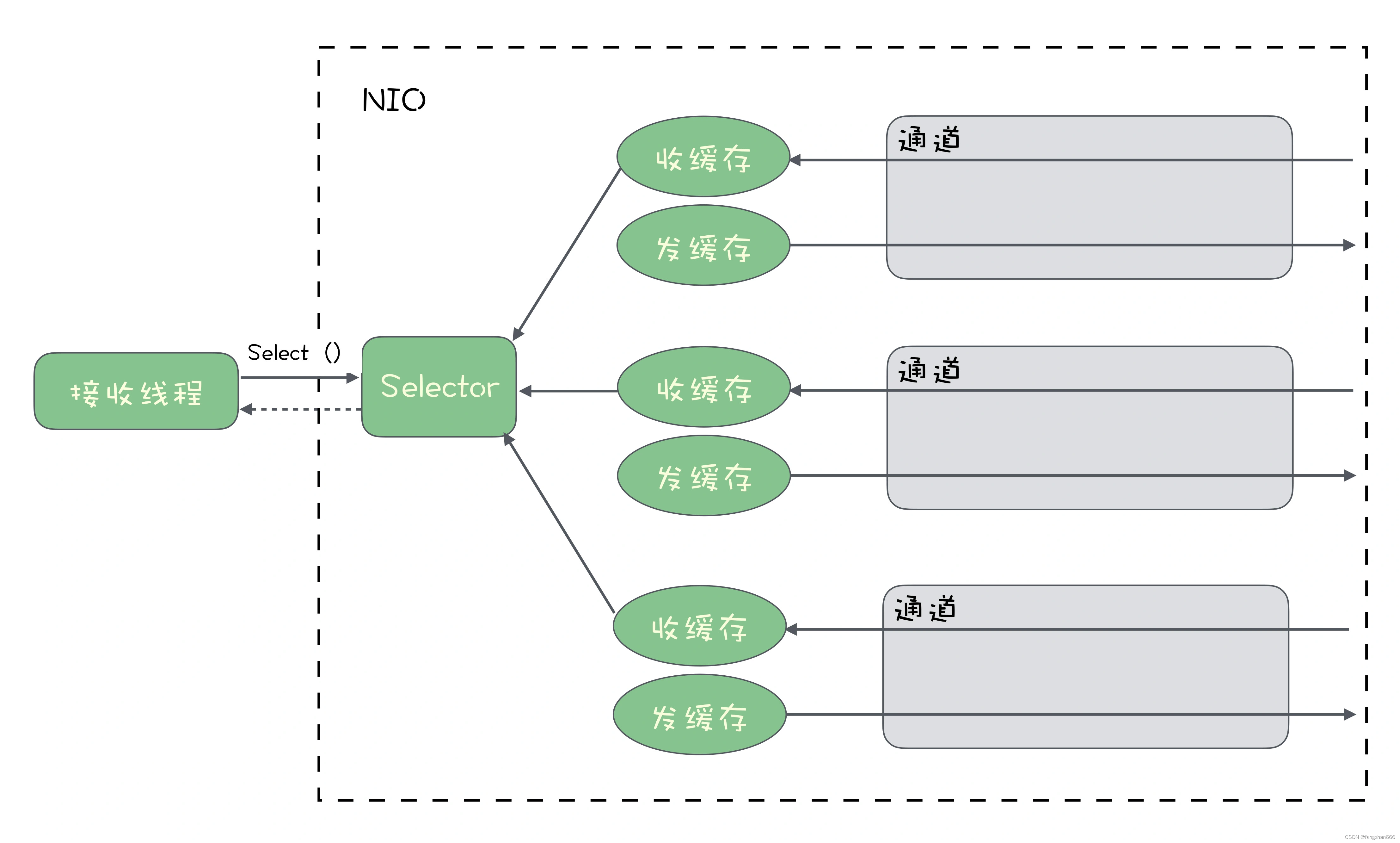
《消息队列高手课》课程学习笔记(八)
如何实现高性能的异步网络传输? **异步与同步模型最大的区别是,同步模型会阻塞线程等待资源,而异步模型不会阻塞线程,它是等资源准备好后,再通知业务代码来完成后续的资源处理逻辑。**这种异步设计的方法,…...

DC电源模块在工业自动化的应用
BOSHIDA DC电源模块在工业自动化的应用 随着自动化技术的不断发展,DC电源模块已成为工业控制系统中不可或缺的一个组成部分。在许多自动化系统中,如机器人、控制器、PLC等,都需要使用到直流电源模块来提供稳定可靠的电源,以确保系…...

Java容器-集合
目录 1.Java容器概述 2.集合框架 3.Collection接口中的方法使用 4.iterator() 5.List接口 2.ArrayList、LinkedList、Vector相同点 3.不同点 1.ArrayList 2.LinkedList 3.Vector 4.Vector源码分析 5.ArrayList源码分析 6.LinkedList源码分析 6.List中的常用方法 …...
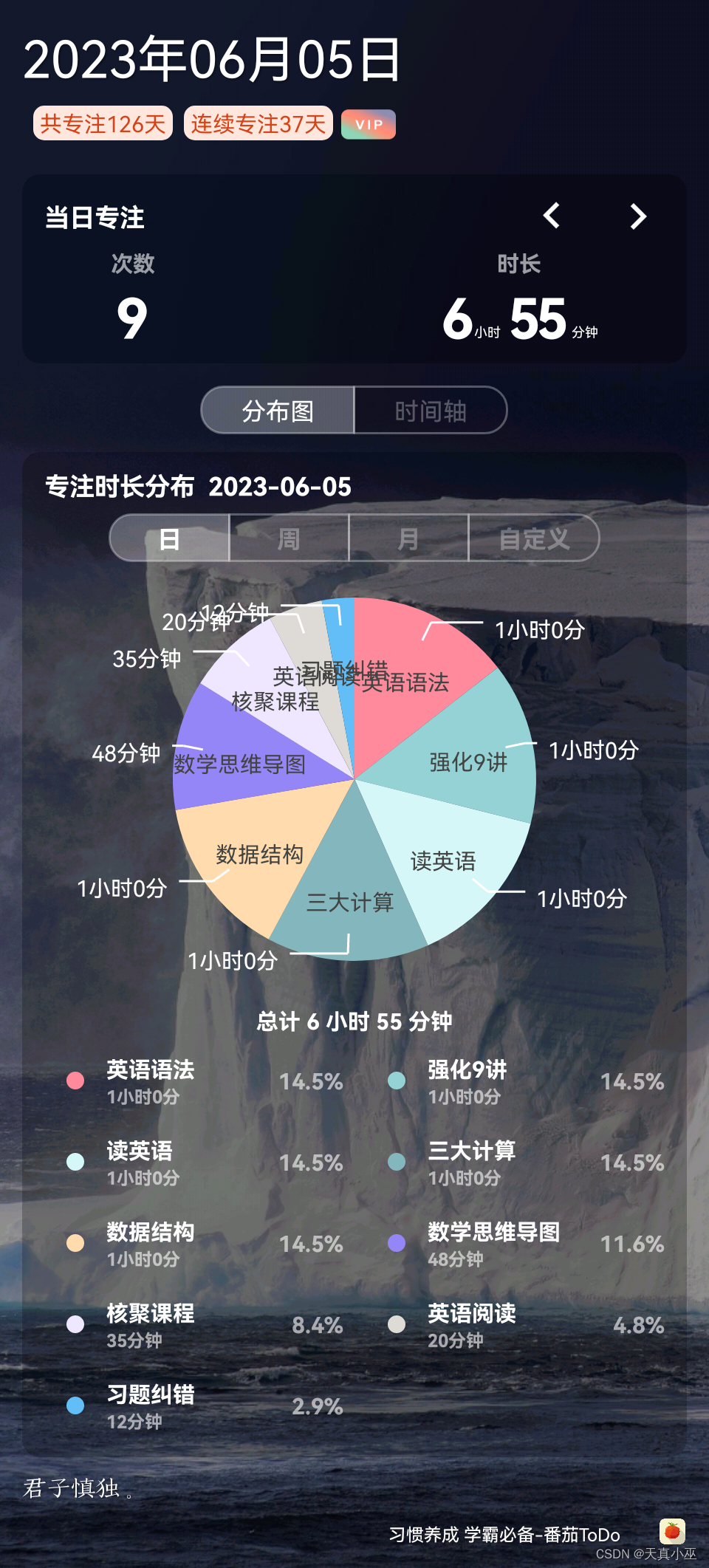
总结890
学习目标: 月目标:6月(线性代数强化9讲2遍,背诵15篇短文,考研核心词过三遍) 周目标:线性代数强化3讲,英语背3篇文章并回诵,检测 每日必复习(5分钟ÿ…...

2023年5月青少年机器人技术等级考试理论综合试卷(二级)
青少年机器人技术等级考试理论综合试卷(二级)2023.6 分数: 100 题数: 45 一、 单选题(共 30 题, 共 60 分) 1.下图中的凸轮机构使用了摆动型从动件的是? ( ) A.a B.b C.c D.d 试题类…...

2023CCPC河南省赛 VP记录
感觉现在的xcpc,风格越来越像CF,不是很喜欢,还是更喜欢多点算法题的比赛 VP银了,VP银也是银 感觉省赛都是思维题,几乎没有算法题,感觉像打了场大型的CF B题很简单没开出来,一直搞到最后&…...
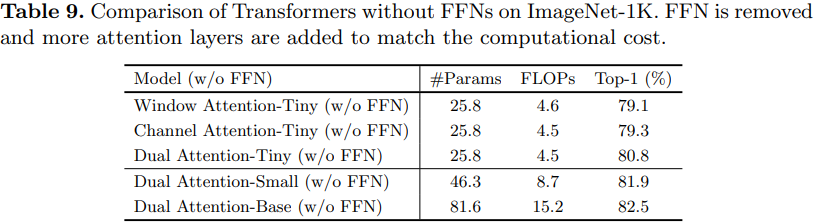
【ECCV2022】DaViT: Dual Attention Vision Transformers
DaViT: Dual Attention Vision Transformers, ECCV2022 解读:【ECCV2022】DaViT: Dual Attention Vision Transformers - 高峰OUC - 博客园 (cnblogs.com) DaViT:双注意力Vision Transformer - 知乎 (zhihu.com) DaViT: Dual Attention Vision Trans…...

Apache 配置与应用
Apache 配置与应用 一、构建虚拟 Web 主机httpd服务支持的虚拟主机类型包括以下三种: 二、基于域名的虚拟主机1.为虚拟主机提供域名解析方法一:部署DNS域名解析服务器 来提供域名解析方法二:在/etc/hosts 文件中临时配置域名与IP地址的映射关…...

测试微信模版消息推送
进入“开发接口管理”--“公众平台测试账号”,无需申请公众账号、可在测试账号中体验并测试微信公众平台所有高级接口。 获取access_token: 自定义模版消息: 关注测试号:扫二维码关注测试号。 发送模版消息: import requests da…...

1688商品列表API与其他数据源的对接思路
将1688商品列表API与其他数据源对接时,需结合业务场景设计数据流转链路,重点关注数据格式兼容性、接口调用频率控制及数据一致性维护。以下是具体对接思路及关键技术点: 一、核心对接场景与目标 商品数据同步 场景:将1688商品信息…...

汽车生产虚拟实训中的技能提升与生产优化
在制造业蓬勃发展的大背景下,虚拟教学实训宛如一颗璀璨的新星,正发挥着不可或缺且日益凸显的关键作用,源源不断地为企业的稳健前行与创新发展注入磅礴强大的动力。就以汽车制造企业这一极具代表性的行业主体为例,汽车生产线上各类…...

学习STC51单片机31(芯片为STC89C52RCRC)OLED显示屏1
每日一言 生活的美好,总是藏在那些你咬牙坚持的日子里。 硬件:OLED 以后要用到OLED的时候找到这个文件 OLED的设备地址 SSD1306"SSD" 是品牌缩写,"1306" 是产品编号。 驱动 OLED 屏幕的 IIC 总线数据传输格式 示意图 …...

Caliper 配置文件解析:config.yaml
Caliper 是一个区块链性能基准测试工具,用于评估不同区块链平台的性能。下面我将详细解释你提供的 fisco-bcos.json 文件结构,并说明它与 config.yaml 文件的关系。 fisco-bcos.json 文件解析 这个文件是针对 FISCO-BCOS 区块链网络的 Caliper 配置文件,主要包含以下几个部…...

项目部署到Linux上时遇到的错误(Redis,MySQL,无法正确连接,地址占用问题)
Redis无法正确连接 在运行jar包时出现了这样的错误 查询得知问题核心在于Redis连接失败,具体原因是客户端发送了密码认证请求,但Redis服务器未设置密码 1.为Redis设置密码(匹配客户端配置) 步骤: 1).修…...

Java多线程实现之Thread类深度解析
Java多线程实现之Thread类深度解析 一、多线程基础概念1.1 什么是线程1.2 多线程的优势1.3 Java多线程模型 二、Thread类的基本结构与构造函数2.1 Thread类的继承关系2.2 构造函数 三、创建和启动线程3.1 继承Thread类创建线程3.2 实现Runnable接口创建线程 四、Thread类的核心…...
)
安卓基础(aar)
重新设置java21的环境,临时设置 $env:JAVA_HOME "D:\Android Studio\jbr" 查看当前环境变量 JAVA_HOME 的值 echo $env:JAVA_HOME 构建ARR文件 ./gradlew :private-lib:assembleRelease 目录是这样的: MyApp/ ├── app/ …...

基于IDIG-GAN的小样本电机轴承故障诊断
目录 🔍 核心问题 一、IDIG-GAN模型原理 1. 整体架构 2. 核心创新点 (1) 梯度归一化(Gradient Normalization) (2) 判别器梯度间隙正则化(Discriminator Gradient Gap Regularization) (3) 自注意力机制(Self-Attention) 3. 完整损失函数 二…...

Vue ③-生命周期 || 脚手架
生命周期 思考:什么时候可以发送初始化渲染请求?(越早越好) 什么时候可以开始操作dom?(至少dom得渲染出来) Vue生命周期: 一个Vue实例从 创建 到 销毁 的整个过程。 生命周期四个…...
