卡尔曼滤波与组合导航原理(十二)扩展卡尔曼滤波:EKF、二阶EKF、迭代EKF
文章目录
- 一、多元向量的泰勒级数展开
- 二、扩展Kalman滤波
- 三、二阶滤波
- 四、迭代EKF滤波
一、多元向量的泰勒级数展开
{ y 1 = f 1 ( X ) = f 1 ( x 1 , x 2 , ⋯ x n ) y 2 = f 2 ( X ) = f 2 ( x 1 , x 2 , ⋯ x n ) ⋮ y m = f m ( X ) = f m ( x 1 , x 2 , ⋯ x n ) \left\{\begin{array}{c} y_{1}=f_{1}(\boldsymbol{X})=f_{1}\left(x_{1}, x_{2}, \cdots x_{n}\right) \\ y_{2}=f_{2}(\boldsymbol{X})=f_{2}\left(x_{1}, x_{2}, \cdots x_{n}\right) \\ \quad \vdots \\ y_{m}=f_{m}(\boldsymbol{X})=f_{m}\left(x_{1}, x_{2}, \cdots x_{n}\right) \end{array}\right. ⎩ ⎨ ⎧y1=f1(X)=f1(x1,x2,⋯xn)y2=f2(X)=f2(x1,x2,⋯xn)⋮ym=fm(X)=fm(x1,x2,⋯xn)
上面线性方差组,写成向量形式就是:
Y = f ( X ) \boldsymbol{Y} = \boldsymbol{f} \left( \boldsymbol{X}\right) Y=f(X)
泰勒展开式为:
Y = f ( X ( 0 ) ) + ∑ i = 1 ∞ 1 i ! ( ∇ T ⋅ δ X ) i f ( X ( 0 ) ) \boldsymbol{Y}=\boldsymbol{f}\left(\boldsymbol{X}^{(0)}\right)+\sum_{i=1}^{\infty} \frac{1}{i !}\left(\nabla^{\mathrm{T}} \cdot \delta \boldsymbol{X}\right)^{i} \boldsymbol{f}\left(\boldsymbol{X}^{(0)}\right) Y=f(X(0))+i=1∑∞i!1(∇T⋅δX)if(X(0))
其中 δ X = X − X ( 0 ) \delta \boldsymbol{X}=\boldsymbol{X}-\boldsymbol{X}^{(0)} δX=X−X(0) , ∇ = [ ∂ ∂ x 1 ∂ ∂ x 2 ⋯ ∂ ∂ x n ] T \nabla=\left[\begin{array}{llll}\frac{\partial}{\partial x{1}} & \frac{\partial}{\partial x{2}} & \cdots & \frac{\partial}{\partial x_{n}}\end{array}\right]^{\mathrm{T}} ∇=[∂x1∂∂x2∂⋯∂xn∂]T
一阶导代表梯度、二阶导代表曲率半径
一阶展开项的详细展开式:
标量的求导运算对向量求导是对向量里的每一个元素求导, m m m 列多元函数对 n n n 行的自变量求导:
1 1 ( ∇ T ⋅ δ X ) ′ f ( X ( 0 ) ) = ( ∂ ∂ x 1 δ x 1 + ∂ ∂ x 2 δ x 2 + ⋯ + ∂ ∂ x n δ x n ) f ( X ) ∣ X = X ( 0 ) = [ ∂ f 1 ( X ) ∂ x 1 δ x 1 + ∂ f 1 ( X ) ∂ x 2 δ x 2 + ⋯ + ∂ f 1 ( X ) ∂ x n δ x n ∂ f 2 ( X ) ∂ x 1 δ x 1 + ∂ f 2 ( X ) ∂ x 2 δ x 2 + ⋯ + ∂ f 2 ( X ) ∂ x n δ x n ∂ f m ( X ) ∂ x 1 δ x 1 + ∂ f m ( X ) ∂ x 2 δ x 2 + ⋯ + ∂ f m ( X ) ∂ x n δ x n ] X = X ( 0 ) = [ ∂ f 1 ( X ) ∂ x 1 ∂ f 1 ( X ) ∂ x 2 ⋯ ∂ f 1 ( X ) ∂ x n ∂ f 2 ( X ) ∂ x 1 ∂ f 2 ( X ) ∂ x 2 ⋯ ∂ f 2 ( X ) ∂ x n ⋮ ⋮ ⋱ ⋮ ∂ f m ( X ) ∂ x 1 ∂ f m ( X ) ∂ x 2 ⋯ ∂ f m ( X ) ∂ x n ] δ [ δ x 1 δ x 2 ⋮ δ x n ] X = X ( 0 ) = J ( f ( X ) ) δ X ∣ X = X ( 0 ) \begin{array}{l} \frac{1}{1}\left(\nabla^{\mathrm{T}} \cdot \delta \boldsymbol{X}\right)^{\prime} \boldsymbol{f}\left(\boldsymbol{X}^{(0)}\right)=\left.\left(\frac{\partial}{\partial x_{1}} \delta x_{1}+\frac{\partial}{\partial x_{2}} \delta x_{2}+\cdots+\frac{\partial}{\partial x_{n}} \delta x_{n}\right) \boldsymbol{f}(\boldsymbol{X})\right|_{\boldsymbol{X}=\boldsymbol{X}^{(0)}} \\ =\left[\begin{array}{c} \frac{\partial f_{1}(\boldsymbol{X})}{\partial x_{1}} \delta x_{1}+\frac{\partial f_{1}(\boldsymbol{X})}{\partial x_{2}} \delta x_{2}+\cdots+\frac{\partial f_{1}(\boldsymbol{X})}{\partial x_{n}} \delta x_{n} \\ \frac{\partial f_{2}(\boldsymbol{X})}{\partial x_{1}} \delta x_{1}+\frac{\partial f_{2}(\boldsymbol{X})}{\partial x_{2}} \delta x_{2}+\cdots+\frac{\partial f_{2}(\boldsymbol{X})}{\partial x_{n}} \delta x_{n} \\ \frac{\partial f_{m}(\boldsymbol{X})}{\partial x_{1}} \delta x_{1}+\frac{\partial f_{m}(\boldsymbol{X})}{\partial x_{2}} \delta x_{2}+\cdots+\frac{\partial f_{m}(\boldsymbol{X})}{\partial x_{n}} \delta x_{n} \end{array}\right]_{\boldsymbol{X}=\boldsymbol{X}^{(0)}}=\left[\begin{array}{cccc} \frac{\partial f_{1}(\boldsymbol{X})}{\partial x_{1}} & \frac{\partial f_{1}(\boldsymbol{X})}{\partial x_{2}} & \cdots & \frac{\partial f_{1}(\boldsymbol{X})}{\partial x_{n}} \\ \frac{\partial f_{2}(\boldsymbol{X})}{\partial x_{1}} & \frac{\partial f_{2}(\boldsymbol{X})}{\partial x_{2}} & \cdots & \frac{\partial f_{2}(\boldsymbol{X})}{\partial x_{n}} \\ \vdots & \vdots & \ddots & \vdots \\ \frac{\partial f_{m}(\boldsymbol{X})}{\partial x_{1}} & \frac{\partial f_{m}(\boldsymbol{X})}{\partial x_{2}} & \cdots & \frac{\partial f_{m}(\boldsymbol{X})}{\partial x_{n}} \end{array}\right]^{\delta}\left[\begin{array}{c} \delta x_{1} \\ \delta x_{2} \\ \vdots \\ \delta x_{n} \end{array}\right]_{X=X^{(0)}} \\ =\left.J(\boldsymbol{f}(\boldsymbol{X})) \delta \boldsymbol{X}\right|_{X=X^{(0)}} \quad \\ \end{array} 11(∇T⋅δX)′f(X(0))=(∂x1∂δx1+∂x2∂δx2+⋯+∂xn∂δxn)f(X) X=X(0)= ∂x1∂f1(X)δx1+∂x2∂f1(X)δx2+⋯+∂xn∂f1(X)δxn∂x1∂f2(X)δx1+∂x2∂f2(X)δx2+⋯+∂xn∂f2(X)δxn∂x1∂fm(X)δx1+∂x2∂fm(X)δx2+⋯+∂xn∂fm(X)δxn X=X(0)= ∂x1∂f1(X)∂x1∂f2(X)⋮∂x1∂fm(X)∂x2∂f1(X)∂x2∂f2(X)⋮∂x2∂fm(X)⋯⋯⋱⋯∂xn∂f1(X)∂xn∂f2(X)⋮∂xn∂fm(X) δ δx1δx2⋮δxn X=X(0)=J(f(X))δX∣X=X(0)
其中 ∫ J ( f ( X ) ) = ∂ f ( X ) ∂ X T \int J(\boldsymbol{f}(\boldsymbol{X}))=\frac{\partial \boldsymbol{f}(\boldsymbol{X})}{\partial \boldsymbol{X}^{\mathrm{T}}} ∫J(f(X))=∂XT∂f(X) 可称之为雅各比矩阵, m m m 列多元函数对 n n n 行的自变量求一阶导得到的矩阵。
二阶展开项详细表达式:
1 2 ( ∇ T ⋅ δ X ) 2 f ( X ( 0 ) ) = 1 2 ( ∂ ∂ x 1 δ x 1 + ∂ ∂ x 2 δ x 2 + ⋯ + ∂ ∂ x n δ x n ) 2 f ( X ) ∣ X = X ( 0 ) = 1 2 tr ( [ ∂ 2 ∂ x 1 2 ∂ 2 ∂ x 1 ∂ x 2 ⋯ ∂ 2 ∂ x 1 ∂ x n ∂ 2 ∂ x 2 ∂ x 1 ∂ 2 ∂ x 2 2 ⋯ ∂ 2 ∂ x 2 ∂ x n ⋮ ⋮ ⋱ ⋮ ∂ 2 ∂ x n ∂ x 1 ∂ 2 ∂ x n ∂ x 2 ⋯ ∂ 2 ∂ x n 2 ] [ δ x 1 2 δ x 1 δ x 2 ⋯ δ x 1 δ x n δ x 2 δ x 1 δ x 2 2 ⋯ δ x 2 δ x n ⋮ ⋮ ⋱ ⋮ δ x n δ x 1 δ x n δ x 2 ⋯ δ x n 2 ] ) f ( X ) ∣ X = X ( 0 ) = 1 2 tr ( ∇ ∇ T ⋅ δ X δ X T ) f ( X ) ∣ X = X ( 0 ) = 1 2 tr ( ∇ ∇ T ⋅ δ X δ X T ) ∑ j = 1 m e j f j ( X ) ∣ X = X ( 0 ) = 1 2 ∑ j = 1 m e j tr ( ∇ ∇ T ⋅ δ X δ X T ) f j ( X ) ∣ X = X ( 0 ) = 1 2 ∑ j = 1 m e j tr ( ∇ ∇ T f j ( X ) ∣ X = X ( 0 ) ⋅ δ X δ X T ) = 1 2 ∑ j = 1 m e j tr ( H ( f j ( X ) ∣ X = X ( 0 ) ⋅ δ X δ X T ) \begin{array}{l} \frac{1}{2}\left(\nabla^{\mathrm{T}} \cdot \delta \boldsymbol{X}\right)^{2} \boldsymbol{f}\left(\boldsymbol{X}^{(0)}\right)=\left.\frac{1}{2}\left(\frac{\partial}{\partial x_{1}} \delta x_{1}+\frac{\partial}{\partial x_{2}} \delta x_{2}+\cdots+\frac{\partial}{\partial x_{n}} \delta x_{n}\right)^{2} \boldsymbol{f}(\boldsymbol{X})\right|_{X=X^{(0)}} \\ =\left.\frac{1}{2} \operatorname{tr}\left(\left[\begin{array}{cccc} \frac{\partial^{2}}{\partial x_{1}^{2}} & \frac{\partial^{2}}{\partial x_{1} \partial x_{2}} & \cdots & \frac{\partial^{2}}{\partial x_{1} \partial x_{n}} \\ \frac{\partial^{2}}{\partial x_{2} \partial x_{1}} & \frac{\partial^{2}}{\partial x_{2}^{2}} & \cdots & \frac{\partial^{2}}{\partial x_{2} \partial x_{n}} \\ \vdots & \vdots & \ddots & \vdots \\ \frac{\partial^{2}}{\partial x_{n} \partial x_{1}} & \frac{\partial^{2}}{\partial x_{n} \partial x_{2}} & \cdots & \frac{\partial^{2}}{\partial x_{n}^{2}} \end{array}\right]\left[\begin{array}{cccc} \delta x_{1}^{2} & \delta x_{1} \delta x_{2} & \cdots & \delta x_{1} \delta x_{n} \\ \delta x_{2} \delta x_{1} & \delta x_{2}^{2} & \cdots & \delta x_{2} \delta x_{n} \\ \vdots & \vdots & \ddots & \vdots \\ \delta x_{n} \delta x_{1} & \delta x_{n} \delta x_{2} & \cdots & \delta x_{n}^{2} \end{array}\right]\right) \boldsymbol{f}(\boldsymbol{X})\right|_{X=\mathbf{X}^{(0)}} \\ \begin{array}{l} =\left.\frac{1}{2} \operatorname{tr}\left(\nabla \nabla^{\mathrm{T}} \cdot \delta \boldsymbol{X} \delta \boldsymbol{X}^{\mathrm{T}}\right) \boldsymbol{f}(\boldsymbol{X})\right|_{X=X^{(0)}}=\left.\frac{1}{2} \operatorname{tr}\left(\nabla \nabla^{\mathrm{T}} \cdot \delta \boldsymbol{X} \delta \boldsymbol{X}^{\mathrm{T}}\right) \sum_{j=1}^{m} \boldsymbol{e}_{j} f_{j}(\boldsymbol{X})\right|_{X=X^{(0)}} \\ =\left.\frac{1}{2} \sum_{j=1}^{m} \boldsymbol{e}_{j} \operatorname{tr}\left(\nabla \nabla^{\mathrm{T}} \cdot \delta \boldsymbol{X} \delta \boldsymbol{X}^{\mathrm{T}}\right) f_{j}(\boldsymbol{X})\right|_{X=X^{(0)}}=\frac{1}{2} \sum_{j=1}^{m} \boldsymbol{e}_{j} \operatorname{tr}\left(\left.\nabla \nabla^{\mathrm{T}} f_{j}(\boldsymbol{X})\right|_{X=X^{(0)}} \cdot \delta \boldsymbol{X} \delta \boldsymbol{X}^{\mathrm{T}}\right) \end{array} \\ =\frac{1}{2} \sum_{j=1}^{m} \boldsymbol{e}_{j} \operatorname{tr}\left(\mathscr{H}\left(\left.f_{j}(\boldsymbol{X})\right|_{X=X^{(0)}} \cdot \delta \boldsymbol{X} \delta \boldsymbol{X}^{\mathrm{T}}\right) \quad\right. \\ \end{array} 21(∇T⋅δX)2f(X(0))=21(∂x1∂δx1+∂x2∂δx2+⋯+∂xn∂δxn)2f(X) X=X(0)=21tr ∂x12∂2∂x2∂x1∂2⋮∂xn∂x1∂2∂x1∂x2∂2∂x22∂2⋮∂xn∂x2∂2⋯⋯⋱⋯∂x1∂xn∂2∂x2∂xn∂2⋮∂xn2∂2 δx12δx2δx1⋮δxnδx1δx1δx2δx22⋮δxnδx2⋯⋯⋱⋯δx1δxnδx2δxn⋮δxn2 f(X) X=X(0)=21tr(∇∇T⋅δXδXT)f(X) X=X(0)=21tr(∇∇T⋅δXδXT)∑j=1mejfj(X) X=X(0)=21∑j=1mejtr(∇∇T⋅δXδXT)fj(X) X=X(0)=21∑j=1mejtr(∇∇Tfj(X) X=X(0)⋅δXδXT)=21∑j=1mejtr(H(fj(X)∣X=X(0)⋅δXδXT)
Y = f ( X ( 0 ) ) + J ( f ( X ( 0 ) ) ) δ X + 1 2 ∑ i = 1 m e i tr ( H ( f i ( X ( 0 ) ) ) ⋅ δ X δ X T ) + O 3 \boldsymbol{Y}=\boldsymbol{f}\left(\boldsymbol{X}^{(0)}\right)+J\left(f\left(X^{(0)}\right)\right) \delta \boldsymbol{X}+\frac{1}{2} \sum_{i=1}^{m} e_{i} \operatorname{tr}\left(\mathscr{H}\left(f_{i}\left(X^{(0)}\right)\right) \cdot \delta \boldsymbol{X} \delta \boldsymbol{X}^{\mathrm{T}}\right)+O^{3} Y=f(X(0))+J(f(X(0)))δX+21i=1∑meitr(H(fi(X(0)))⋅δXδXT)+O3
其中 H \mathscr{H} H 为海森矩阵, m m m 列多元函数对 n n n 行的自变量求二阶导得到的矩阵,m 个向量函数有 m 个海森矩阵。
二、扩展Kalman滤波
遇到非线性的状态空间模型时,对状态方程和量测方程做线性化处理,取泰勒展开的一阶项。
状态空间模型(加性噪声,噪声和状态直接是相加的)
这里简单的用加性噪声模型表示,一般形式为 X k = f ( X k − 1 , W k − 1 , k − 1 ) \boldsymbol{X}_{k}=\boldsymbol{f}\left(\boldsymbol{X}_{k-1}, \boldsymbol{W}_{k-1}, k-1\right) Xk=f(Xk−1,Wk−1,k−1) ,非线性更强,更一般,可以表示噪声和状态之间复杂的关系
{ X k = f ( X k − 1 ) + Γ k − 1 W k − 1 Z k = h ( X k ) + V k \left\{\begin{array}{l}\boldsymbol{X}_{k}=\boldsymbol{f}\left(\boldsymbol{X}_{k-1}\right)+\boldsymbol{\Gamma}_{k-1} \boldsymbol{W}_{k-1} \\ \boldsymbol{Z}_{k}=\boldsymbol{h}\left(\boldsymbol{X}_{k}\right)+\boldsymbol{V}_{k}\end{array}\right. {Xk=f(Xk−1)+Γk−1Wk−1Zk=h(Xk)+Vk
选择 k − 1 k-1 k−1 时刻参考值 X k − 1 n \boldsymbol{X}_{k-1}^{n} Xk−1n ,参考点和真实值偏差 δ X k − 1 = X k − 1 − X k − 1 n \delta \boldsymbol{X}_{k-1}=\boldsymbol{X}_{k-1}-\boldsymbol{X}_{k-1}^{n} δXk−1=Xk−1−Xk−1n
状态一步预测:上一时刻参考点带入状态方程 X k / k − 1 n = f ( X k − 1 n ) \boldsymbol{X}_{k / k-1}^{n}=\boldsymbol{f}\left(\boldsymbol{X}_{k-1}^{n}\right) Xk/k−1n=f(Xk−1n) ,预测值的偏差 δ X k = X k − X k / k − 1 n \delta \boldsymbol{X}_{k}=\boldsymbol{X}_{k}-\boldsymbol{X}_{k / k-1}^{n} δXk=Xk−Xk/k−1n 。
量测一步预测: Z k / k − 1 n = h ( X k / k − 1 n ) \boldsymbol{Z}_{k / k-1}^{n}=\boldsymbol{h}\left(\boldsymbol{X}_{k / k-1}^{n}\right) Zk/k−1n=h(Xk/k−1n) ,偏差 δ Z k = Z k − Z k / k − 1 n \delta \boldsymbol{Z}_{k}=\boldsymbol{Z}_{k}-\boldsymbol{Z}_{k / k-1}^{n} δZk=Zk−Zk/k−1n 。
展开得状态偏差方程:
X k ≈ f ( X k − 1 n ) + J ( f ( X k − 1 n ) ) ( X k − 1 − X k − 1 n ) + Γ k − 1 W k − 1 X k − f ( X k − 1 n ) ≈ Φ k / k − 1 n ( X k − 1 − X k − 1 n ) + Γ k − 1 W k − 1 δ X k = Φ k / k − 1 n δ X k − 1 + Γ k − 1 W k − 1 \begin{array}{ll} & \boldsymbol{X}_{k} \approx \boldsymbol{f}\left(\boldsymbol{X}_{k-1}^{n}\right)+\boldsymbol{J}\left(\boldsymbol{f}\left(\boldsymbol{X}_{k-1}^{n}\right)\right)\left(\boldsymbol{X}_{k-1}-\boldsymbol{X}_{k-1}^{n}\right)+\boldsymbol{\Gamma}_{k-1} \boldsymbol{W}_{k-1} \\ & \boldsymbol{X}_{k}-\boldsymbol{f}\left(\boldsymbol{X}_{k-1}^{n}\right) \approx \boldsymbol{\Phi}_{k / k-1}^{n}\left(\boldsymbol{X}_{k-1}-\boldsymbol{X}_{k-1}^{n}\right)+\boldsymbol{\Gamma}_{k-1} \boldsymbol{W}_{k-1} \\ & \delta \boldsymbol{X}_{k}=\boldsymbol{\Phi}_{k / k-1}^{n} \delta \boldsymbol{X}_{k-1}+\boldsymbol{\Gamma}_{k-1} \boldsymbol{W}_{k-1} \end{array} Xk≈f(Xk−1n)+J(f(Xk−1n))(Xk−1−Xk−1n)+Γk−1Wk−1Xk−f(Xk−1n)≈Φk/k−1n(Xk−1−Xk−1n)+Γk−1Wk−1δXk=Φk/k−1nδXk−1+Γk−1Wk−1
展开得量测偏差方程:
Z k ≈ h ( X k / k − 1 n ) + J ( h ( X k / k − 1 n ) ) ( X k − X k / k − 1 n ) + V k δ Z k = H k n δ X k + V k \begin{array}{ll} & \boldsymbol{Z}_{k} \approx \boldsymbol{h}\left(\boldsymbol{X}_{k / k-1}^{n}\right)+\boldsymbol{J}\left(\boldsymbol{h}\left(\boldsymbol{X}_{k / k-1}^{n}\right)\right)\left(\boldsymbol{X}_{k}-\boldsymbol{X}_{k / k-1}^{n}\right)+\boldsymbol{V}_{k} \\ & \delta \boldsymbol{Z}_{k}=\boldsymbol{H}_{k}^{n} \delta \boldsymbol{X}_{k}+\boldsymbol{V}_{k} \end{array} Zk≈h(Xk/k−1n)+J(h(Xk/k−1n))(Xk−Xk/k−1n)+VkδZk=HknδXk+Vk
得偏差状态空间估计模型:
{ δ X k = Φ k ∣ k − 1 n δ X k − 1 + Γ k − 1 W k − 1 δ Z k = H k n δ X k + V k \left\{\begin{array}{l}\delta \boldsymbol{X}_{k}=\boldsymbol{\Phi}_{k \mid k-1}^{n} \delta \boldsymbol{X}_{k-1}+\boldsymbol{\Gamma}_{k-1} \boldsymbol{W}_{k-1} \\ \delta \boldsymbol{Z}_{k}=\boldsymbol{H}_{k}^{n} \delta \boldsymbol{X}_{k}+\boldsymbol{V}_{k}\end{array}\right. {δXk=Φk∣k−1nδXk−1+Γk−1Wk−1δZk=HknδXk+Vk
偏差量是线性的了,可以用Kalman滤波进行处理:
滤波更新方程: δ X ^ k = Φ k / k − 1 n δ X ^ k − 1 + K k n ( δ Z k − H k n Φ k / k − 1 n δ X ^ k − 1 ) {\color{red}\delta \hat{\boldsymbol{X}}_{k}}=\boldsymbol{\Phi}_{k / k-1}^{n} {\color{green}\delta \hat{\boldsymbol{X}}_{k-1}}+\boldsymbol{K}_{k}^{n}\left(\delta \boldsymbol{Z}_{k}-\boldsymbol{H}_{k}^{n} \boldsymbol{\Phi}_{k / k-1}^{n} {\color{green}\delta \hat{\boldsymbol{X}}_{k-1}}\right) δX^k=Φk/k−1nδX^k−1+Kkn(δZk−HknΦk/k−1nδX^k−1)
⟶ δ X ^ k = X ^ k − X k / k − 1 n δ X ^ k − 1 = X ^ k − 1 − X k − 1 n X ^ k = X k / k − 1 n + K k n ( Z k − Z k / k − 1 n ) + ( I − K k n H k n ) Φ k / k − 1 n ( X ^ k − 1 − X k − 1 n ) ⟶ X k − 1 n = X ^ k − 1 = X k / k − 1 n + K k n ( Z k − Z k / k − 1 n ) \begin{array}{l} \underset{\delta \hat{\boldsymbol{X}}_{k-1}=\hat{\boldsymbol{X}}_{k-1}-\boldsymbol{X}_{k-1}^{n}}{\underset{\delta \hat{\boldsymbol{X}}_{k}=\hat{\boldsymbol{X}}_{k}-\boldsymbol{X}_{k / k-1}^{n}}{\longrightarrow}} \hat{\boldsymbol{X}}_{k}=\boldsymbol{X}_{k / k-1}^{n}+\boldsymbol{K}_{k}^{n}\left(\boldsymbol{Z}_{k}-\boldsymbol{Z}_{k / k-1}^{n}\right)+\left(\boldsymbol{I}-\boldsymbol{K}_{k}^{n} \boldsymbol{H}_{k}^{n}\right) \boldsymbol{\Phi}_{k / k-1}^{n}\left(\hat{\boldsymbol{X}}_{k-1}-\boldsymbol{X}_{k-1}^{n}\right) \\ \stackrel{\boldsymbol{X}_{k-1}^{n}=\hat{\boldsymbol{X}}_{k-1}}{\longrightarrow}=\boldsymbol{X}_{k / k-1}^{n}+\boldsymbol{K}_{k}^{n}\left(\boldsymbol{Z}_{k}-\boldsymbol{Z}_{k / k-1}^{n}\right) \end{array} δX^k−1=X^k−1−Xk−1nδX^k=X^k−Xk/k−1n⟶X^k=Xk/k−1n+Kkn(Zk−Zk/k−1n)+(I−KknHkn)Φk/k−1n(X^k−1−Xk−1n)⟶Xk−1n=X^k−1=Xk/k−1n+Kkn(Zk−Zk/k−1n)
将 δ X ^ k − 1 = X ^ k − 1 − X k − 1 n {\color{green}\delta \hat{\boldsymbol{X}}_{k-1}=\hat{\boldsymbol{X}}_{k-1}-\boldsymbol{X}_{k-1}^{n}} δX^k−1=X^k−1−Xk−1n 和 δ X ^ k = X ^ k − X k / k − 1 n {\color{red}\delta \hat{\boldsymbol{X}}_{k}=\hat{\boldsymbol{X}}_{k}-\boldsymbol{X}_{k / k-1}^{n}} δX^k=X^k−Xk/k−1n 带入得:
X ^ k = X k / k − 1 n + K k n ( Z k − Z k / k − 1 n ) + ( I − K k n H k n ) Φ k / k − 1 n ( X ^ k − 1 − X k − 1 n ) \hat{\boldsymbol{X}}_{k}=\boldsymbol{X}_{k / k-1}^{n}+\boldsymbol{K}_{k}^{n}\left(\boldsymbol{Z}_{k}-\boldsymbol{Z}_{k / k-1}^{n}\right)+{\color{pink} \left(\boldsymbol{I}-\boldsymbol{K}_{k}^{n} \boldsymbol{H}_{k}^{n}\right) \boldsymbol{\Phi}_{k / k-1}^{n}\left(\hat{\boldsymbol{X}}_{k-1}-\boldsymbol{X}_{k-1}^{n}\right)} X^k=Xk/k−1n+Kkn(Zk−Zk/k−1n)+(I−KknHkn)Φk/k−1n(X^k−1−Xk−1n)
此公式就相当于对状态进行操作。前面部分就是Kalman滤波方程。后面多出的粉色部分包含了参考值,令 X k − 1 n = X ^ k − 1 \boldsymbol{X}_{k-1}^{n}=\hat{\boldsymbol{X}}_{k-1} Xk−1n=X^k−1 ,参考点选成上一时刻的估计值,后面一部分就为 0 0 0 ,得
X k / k − 1 n + K k n ( Z k − Z k / k − 1 n ) \boldsymbol{X}_{k / k-1}^{n}+\boldsymbol{K}_{k}^{n}\left(\boldsymbol{Z}_{k}-\boldsymbol{Z}_{k / k-1}^{n}\right) Xk/k−1n+Kkn(Zk−Zk/k−1n)
EKF滤波公式汇总
{ X ^ k / k − 1 = f ( X ^ k − 1 ) P k / k − 1 = Φ k / k − 1 P k − 1 Φ k / k − 1 T + Γ k − 1 Q k − 1 Γ k − 1 T Φ k / k − 1 = J ( f ( X ^ k − 1 ) ) K k = P k / k − 1 H k T ( H k P k / k − 1 H k T + R k ) − 1 H k = J ( h ( X ^ k / k − 1 ) ) X ^ k = X ^ k / k − 1 + K k [ Z k − h ( X ^ k / k − 1 ) ] P k = ( I − K k H k ) P k / k − 1 \left\{\begin{array}{ll}\hat{\boldsymbol{X}}_{k / k-1}=\boldsymbol{f}\left(\hat{\boldsymbol{X}}_{k-1}\right) & \\ \boldsymbol{P}_{k / k-1}={\color{red}\boldsymbol{\Phi}_{k / k-1}} \boldsymbol{P}_{k-1} {\color{red}\boldsymbol{\Phi}_{k / k-1}^{\mathrm{T}}}+\boldsymbol{\Gamma}_{k-1} \boldsymbol{Q}_{k-1} \boldsymbol{\Gamma}_{k-1}^{\mathrm{T}} & {\color{red}\boldsymbol{\Phi}_{k / k-1}=\boldsymbol{J}\left(\boldsymbol{f}\left(\hat{\boldsymbol{X}}_{k-1}\right)\right)} \\ \boldsymbol{K}_{k}=\boldsymbol{P}_{k / k-1} {\color{green}\boldsymbol{H}_{k}^{\mathrm{T}}}\left({\color{green}\boldsymbol{H}_{k}} \boldsymbol{P}_{k / k-1} {\color{green}\boldsymbol{H}_{k}^{\mathrm{T}}}+\boldsymbol{R}_{k}\right)^{-1} & {\color{green}\boldsymbol{H}_{k}=\boldsymbol{J}\left(\boldsymbol{h}\left(\hat{\boldsymbol{X}}_{k / k-1}\right)\right)} \\ \hat{\boldsymbol{X}}_{k}=\hat{\boldsymbol{X}}_{k / k-1}+\boldsymbol{K}_{k}\left[\boldsymbol{Z}_{k}-\boldsymbol{h}\left(\hat{\boldsymbol{X}}_{k / k-1}\right)\right] & \\ \boldsymbol{P}_{k}=\left(\boldsymbol{I}-\boldsymbol{K}_{k} {\color{green}\boldsymbol{H}_{k}}\right) \boldsymbol{P}_{k / k-1} & \end{array}\right. ⎩ ⎨ ⎧X^k/k−1=f(X^k−1)Pk/k−1=Φk/k−1Pk−1Φk/k−1T+Γk−1Qk−1Γk−1TKk=Pk/k−1HkT(HkPk/k−1HkT+Rk)−1X^k=X^k/k−1+Kk[Zk−h(X^k/k−1)]Pk=(I−KkHk)Pk/k−1Φk/k−1=J(f(X^k−1))Hk=J(h(X^k/k−1))
- 状态转移矩阵是状态方程在 k − 1 k-1 k−1 处的一阶偏导组成的雅可比矩阵。
- 设计矩阵是量测方程在 k − 1 k-1 k−1 处的一阶偏导组成的雅可比矩阵。
三、二阶滤波
状态方程的二阶泰勒展开:
X k = f ( X k − 1 n ) + Φ k / k − 1 n δ X + 1 2 ∑ i = 1 n e i tr ( D f i − ⋅ δ X δ X T ) + Γ k − 1 W k − 1 \boldsymbol{X}_{k}=\boldsymbol{f}\left(\boldsymbol{X}_{k-1}^{n}\right)+\boldsymbol{\Phi}_{k / k-1}^{n} \delta \boldsymbol{X}+\frac{1}{2} \sum_{i=1}^{n} \boldsymbol{e}_{i} \operatorname{tr}\left(\boldsymbol{D}_{f i}^{-} \cdot \boldsymbol{\delta} \boldsymbol{X} \delta \boldsymbol{X}^{\mathrm{T}}\right)+\boldsymbol{\Gamma}_{k-1} \boldsymbol{W}_{k-1} Xk=f(Xk−1n)+Φk/k−1nδX+21i=1∑neitr(Dfi−⋅δXδXT)+Γk−1Wk−1
状态预测:上面的方程两边求均值得:
X ^ k / k − 1 = E [ f ( X k − 1 n ) + Φ k / k − 1 n δ X + 1 2 ∑ i = 1 n e i tr ( D f i ⋅ δ X δ X T ) + Γ k − 1 W k − 1 ] = f ( X k − 1 n ) + Φ k / k − 1 n E [ δ X ] + 1 2 ∑ i = 1 n e i tr ( D f i ⋅ E [ δ X δ X T ] ) + Γ k − 1 E [ W k − 1 ] = f ( X k − 1 n ) + 1 2 ∑ i = 1 n e i tr ( D f i P k − 1 ) \begin{aligned} \hat{\boldsymbol{X}}_{k / k-1} & =\mathrm{E}\left[\boldsymbol{f}\left(\boldsymbol{X}_{k-1}^{n}\right)+\boldsymbol{\Phi}_{k / k-1}^{n} \delta \boldsymbol{X}+\frac{1}{2} \sum_{i=1}^{n} \boldsymbol{e}_{i} \operatorname{tr}\left(\boldsymbol{D}_{f i} \cdot \boldsymbol{\delta} \boldsymbol{X} \delta \boldsymbol{X}^{\mathrm{T}}\right)+\boldsymbol{\Gamma}_{k-1} \boldsymbol{W}_{k-1}\right] \\ & =\boldsymbol{f}\left(\boldsymbol{X}_{k-1}^{n}\right)+\boldsymbol{\Phi}_{k / k-1}^{n} \mathrm{E}[\delta \boldsymbol{X}]+\frac{1}{2} \sum_{i=1}^{n} \boldsymbol{e}_{i} \operatorname{tr}\left(\boldsymbol{D}_{f i} \cdot \mathrm{E}\left[\delta \boldsymbol{X} \delta \boldsymbol{X}^{\mathrm{T}}\right]\right)+\boldsymbol{\Gamma}_{k-1} \mathrm{E}\left[\boldsymbol{W}_{k-1}\right] \\ & =\boldsymbol{f}\left(\boldsymbol{X}_{k-1}^{n}\right)+\frac{1}{2} \sum_{i=1}^{n} \boldsymbol{e}_{i} \operatorname{tr}\left(\boldsymbol{D}_{f i} \boldsymbol{P}_{k-1}\right) \end{aligned} X^k/k−1=E[f(Xk−1n)+Φk/k−1nδX+21i=1∑neitr(Dfi⋅δXδXT)+Γk−1Wk−1]=f(Xk−1n)+Φk/k−1nE[δX]+21i=1∑neitr(Dfi⋅E[δXδXT])+Γk−1E[Wk−1]=f(Xk−1n)+21i=1∑neitr(DfiPk−1)
状态预测既和状态的传递有关系,也和方差 P P P 阵有关系,比较麻烦。
状态预测的误差:
X ~ k / k − 1 = X k − X ^ k / k − 1 = Φ k / k − 1 n δ X + 1 2 ∑ i = 1 n e i tr ( D f i ⋅ δ X δ X T ) + Γ k − 1 W k − 1 − 1 2 ∑ i = 1 n e i tr ( D f i P k − 1 ) = Φ k / k − 1 n δ X + 1 2 ∑ i = 1 n e i tr ( D f i ( δ X δ X T − P k − 1 ) ) + Γ k − 1 W k − 1 \begin{aligned} \tilde{\boldsymbol{X}}_{k / k-1} & =\boldsymbol{X}_{k}-\hat{\boldsymbol{X}}_{k / k-1} \\ & =\boldsymbol{\Phi}_{k / k-1}^{n} \delta \boldsymbol{X}+\frac{1}{2} \sum_{i=1}^{n} \boldsymbol{e}_{i} \operatorname{tr}\left(\boldsymbol{D}_{f i} \cdot \delta \boldsymbol{X} \delta \boldsymbol{X}^{\mathrm{T}}\right)+\boldsymbol{\Gamma}_{k-1} \boldsymbol{W}_{k-1}-\frac{1}{2} \sum_{i=1}^{n} \boldsymbol{e}_{i} \operatorname{tr}\left(\boldsymbol{D}_{f i} \boldsymbol{P}_{k-1}\right) \\ & =\boldsymbol{\Phi}_{k / k-1}^{n} \delta \boldsymbol{X}+\frac{1}{2} \sum_{i=1}^{n} \boldsymbol{e}_{i} \operatorname{tr}\left(\boldsymbol{D}_{f i}\left(\delta \boldsymbol{X} \delta \boldsymbol{X}^{\mathrm{T}}-\boldsymbol{P}_{k-1}\right)\right)+\boldsymbol{\Gamma}_{k-1} \boldsymbol{W}_{k-1} \end{aligned} X~k/k−1=Xk−X^k/k−1=Φk/k−1nδX+21i=1∑neitr(Dfi⋅δXδXT)+Γk−1Wk−1−21i=1∑neitr(DfiPk−1)=Φk/k−1nδX+21i=1∑neitr(Dfi(δXδXT−Pk−1))+Γk−1Wk−1
状态预测的方差:比较复杂,最后算下来和四阶矩有关系
P k / k − 1 = E [ X ~ k / k − 1 X ~ k / k − 1 T ] = E [ [ Φ k ∣ k − 1 n δ X + 1 2 ∑ i = 1 n e i tr ( D f i ( δ X δ X T − P k − 1 ) ) + Γ k − 1 W k − 1 ] × [ Φ k l k − 1 n δ X + 1 2 ∑ i = 1 n e i tr ( D f i ( δ X δ X T − P k − 1 ) ) + Γ k − 1 W k − 1 ] T ] = Φ k k / k − 1 n P k − 1 ( Φ k / k − 1 n ) T + 1 4 E [ ∑ i = 1 n e i tr ( D f i ( δ X δ X T − P k − 1 ) ) ( ∑ i = 1 n e i tr ( D f i ( δ X δ X T − P k − 1 ) ) ) T ] + Γ k − 1 Q k − 1 Γ k − 1 T = Φ k / k − 1 n P k − 1 ( Φ k / k − 1 n ) T + 1 4 ∑ i = 1 n ∑ j = 1 n e i e j T E [ tr ( D f i ( δ X δ X T − P k − 1 ) ) ⋅ tr ( D j j ( δ X δ X T − P k − 1 ) ) ] + Γ k − 1 Q k − 1 Γ k − 1 T = Φ k / k − 1 n P k − 1 ( Φ k / k − 1 n ) T + 1 2 ∑ i = 1 n ∑ j = 1 n e i e j T tr ( D f i P k − 1 D f j P k − 1 ) + Γ k − 1 Q k − 1 Γ k − 1 T \begin{array}{l} \boldsymbol{P}_{k / k-1}=\mathrm{E}\left[\tilde{\boldsymbol{X}}_{k / k-1} \tilde{\boldsymbol{X}}_{k / k-1}^{\mathrm{T}}\right] \\ =\mathrm{E}\left[\left[\boldsymbol{\Phi}_{k \mid k-1}^{n} \delta \boldsymbol{X}+\frac{1}{2} \sum_{i=1}^{n} \boldsymbol{e}_{i} \operatorname{tr}\left(\boldsymbol{D}_{f i}\left(\delta \boldsymbol{X} \delta \boldsymbol{X}^{\mathrm{T}}-\boldsymbol{P}_{k-1}\right)\right)+\boldsymbol{\Gamma}_{k-1} \boldsymbol{W}_{k-1}\right]\right. \\ \left.\times\left[\boldsymbol{\Phi}_{k l k-1}^{n} \delta \boldsymbol{X}+\frac{1}{2} \sum_{i=1}^{n} \boldsymbol{e}_{i} \operatorname{tr}\left(\boldsymbol{D}_{f i}\left(\delta \boldsymbol{X} \delta \boldsymbol{X}^{\mathrm{T}}-\boldsymbol{P}_{k-1}\right)\right)+\boldsymbol{\Gamma}_{k-1} \boldsymbol{W}_{k-1}\right]^{\mathrm{T}}\right] \\ =\boldsymbol{\Phi}_{k k / k-1}^{n} \boldsymbol{P}_{k-1}\left(\boldsymbol{\Phi}_{k / k-1}^{n}\right)^{\mathrm{T}} \\ +\frac{1}{4} \mathrm{E}\left[\sum_{i=1}^{n} \boldsymbol{e}_{i} \operatorname{tr}\left(\boldsymbol{D}_{f i}\left(\delta \boldsymbol{X} \delta \boldsymbol{X}^{\mathrm{T}}-\boldsymbol{P}_{k-1}\right)\right)\left(\sum_{i=1}^{n} \boldsymbol{e}_{i} \operatorname{tr}\left(\boldsymbol{D}_{f_{i}}\left(\delta \boldsymbol{X} \delta \boldsymbol{X}^{\mathrm{T}}-\boldsymbol{P}_{k-1}\right)\right)\right)^{\mathrm{T}}\right]+\boldsymbol{\Gamma}_{k-1} \boldsymbol{Q}_{k-1} \boldsymbol{\Gamma}_{k-1}^{\mathrm{T}} \\ =\boldsymbol{\Phi}_{k / k-1}^{n} \boldsymbol{P}_{k-1}\left(\boldsymbol{\Phi}_{k / k-1}^{n}\right)^{\mathrm{T}} \\ +\frac{1}{4} \sum_{i=1}^{n} \sum_{j=1}^{n} \boldsymbol{e}_{i} \boldsymbol{e}_{j}^{\mathrm{T}} \mathrm{E}\left[\operatorname{tr}\left(\boldsymbol{D}_{f i}\left(\delta \boldsymbol{X} \delta \boldsymbol{X}^{\mathrm{T}}-\boldsymbol{P}_{k-1}\right)\right) \cdot \operatorname{tr}\left(\boldsymbol{D}_{j j}\left(\delta \boldsymbol{X} \delta \boldsymbol{X}^{\mathrm{T}}-\boldsymbol{P}_{k-1}\right)\right)\right]+\boldsymbol{\Gamma}_{k-1} \boldsymbol{Q}_{k-1} \boldsymbol{\Gamma}_{k-1}^{\mathrm{T}} \\ =\boldsymbol{\Phi}_{k / k-1}^{n} \boldsymbol{P}_{k-1}\left(\boldsymbol{\Phi}_{k / k-1}^{n}\right)^{\mathrm{T}}+\frac{1}{2} \sum_{i=1}^{n} \sum_{j=1}^{n} \boldsymbol{e}_{\boldsymbol{i}} \boldsymbol{e}_{j}^{\mathrm{T}} \operatorname{tr}\left(\boldsymbol{D}_{f i} \boldsymbol{P}_{k-1} \boldsymbol{D}_{f j} \boldsymbol{P}_{k-1}\right)+\boldsymbol{\Gamma}_{k-1} \boldsymbol{Q}_{k-1} \boldsymbol{\Gamma}_{k-1}^{\mathrm{T}} \\ \end{array} Pk/k−1=E[X~k/k−1X~k/k−1T]=E[[Φk∣k−1nδX+21∑i=1neitr(Dfi(δXδXT−Pk−1))+Γk−1Wk−1]×[Φklk−1nδX+21∑i=1neitr(Dfi(δXδXT−Pk−1))+Γk−1Wk−1]T]=Φkk/k−1nPk−1(Φk/k−1n)T+41E[∑i=1neitr(Dfi(δXδXT−Pk−1))(∑i=1neitr(Dfi(δXδXT−Pk−1)))T]+Γk−1Qk−1Γk−1T=Φk/k−1nPk−1(Φk/k−1n)T+41∑i=1n∑j=1neiejTE[tr(Dfi(δXδXT−Pk−1))⋅tr(Djj(δXδXT−Pk−1))]+Γk−1Qk−1Γk−1T=Φk/k−1nPk−1(Φk/k−1n)T+21∑i=1n∑j=1neiejTtr(DfiPk−1DfjPk−1)+Γk−1Qk−1Γk−1T
量测方程的二阶展开:
Z k / k − 1 = h ( X k / k − 1 n ) + H k n δ X + 1 2 ∑ i = 1 m e i i r ( D h i ⋅ δ X δ X T ) + V k Z_{k / k-1}=h\left(X_{k / k-1}^{n}\right)+\boldsymbol{H}_{k}^{n} \delta \boldsymbol{X}+\frac{1}{2} \sum_{i=1}^{m} e_{i} i r\left(D_{h i} \cdot \delta \boldsymbol{X} \delta \boldsymbol{X}^{\mathrm{T}}\right)+V_{k} Zk/k−1=h(Xk/k−1n)+HknδX+21i=1∑meiir(Dhi⋅δXδXT)+Vk
量测预测:
Z ^ k / k − 1 = h ( X k / k − 1 n ) + 1 2 ∑ i = 1 m e i tr ( D h i P k / k − 1 ) \hat{\boldsymbol{Z}}_{k / k-1}=\boldsymbol{h}\left(\boldsymbol{X}_{k / k-1}^{n}\right)+\frac{1}{2} \sum_{i=1}^{m} e_{i} \operatorname{tr}\left(\boldsymbol{D}_{h i} \boldsymbol{P}_{k / k-1}\right) Z^k/k−1=h(Xk/k−1n)+21i=1∑meitr(DhiPk/k−1)
量测预测方差阵:
P z z , k k − 1 = H k n P k / k − 1 ( H k n ) T + 1 2 ∑ i = 1 m ∑ j = 1 m e i e e j t ( D h i P k / k − 1 D h j P k / k − 1 ) + R k \boldsymbol{P}_{z z, k k-1}=\boldsymbol{H}_{k}^{n} \boldsymbol{P}_{k / k-1}\left(\boldsymbol{H}_{k}^{n}\right)^{\mathrm{T}}+\frac{1}{2} \sum_{i=1}^{m} \sum_{j=1}^{m} \boldsymbol{e}_{i}^{\mathrm{e}} \mathrm{e}_{j}^{\mathrm{t}}\left(\boldsymbol{D}_{h i} \boldsymbol{P}_{k / k-1} \boldsymbol{D}_{hj} \boldsymbol{P}_{k / k-1}\right)+\boldsymbol{R}_{k} Pzz,kk−1=HknPk/k−1(Hkn)T+21i=1∑mj=1∑meieejt(DhiPk/k−1DhjPk/k−1)+Rk
状态/量测互协方差阵:
P x z , k k − 1 = P k / k − 1 H k n \boldsymbol{P}_{x z, k k-1}=\boldsymbol{P}_{k / k-1} \boldsymbol{H}_{k}^{n} Pxz,kk−1=Pk/k−1Hkn
最后,得二阶滤波公式:红色部分是二阶多出来的,运算量巨大收益微小
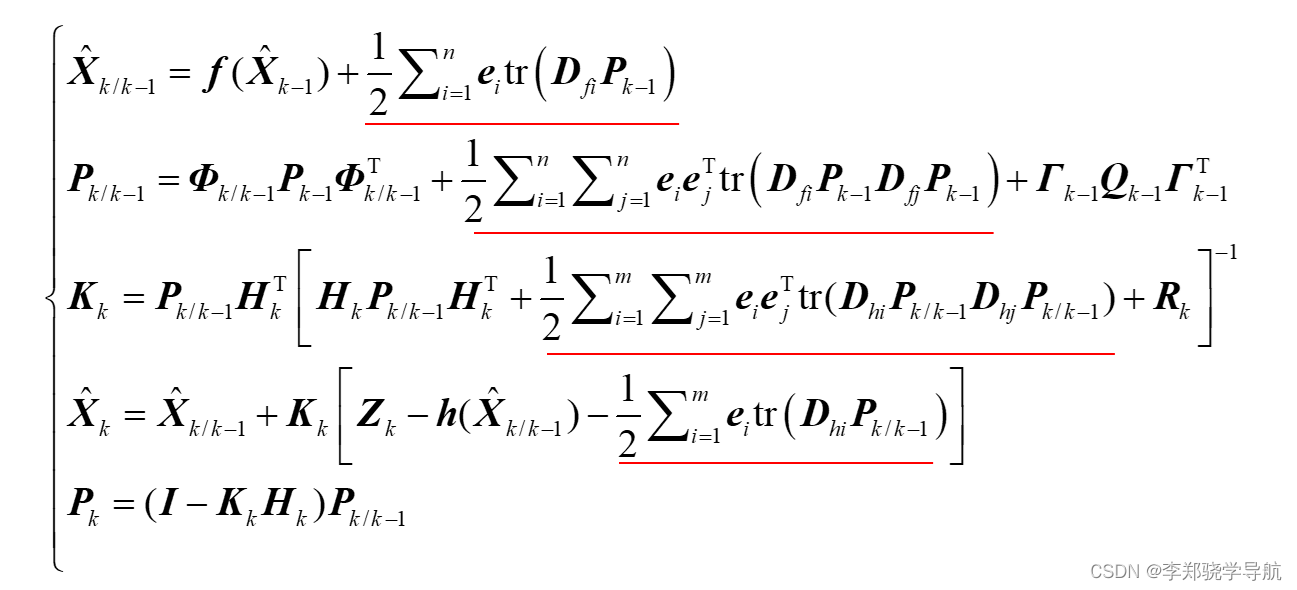
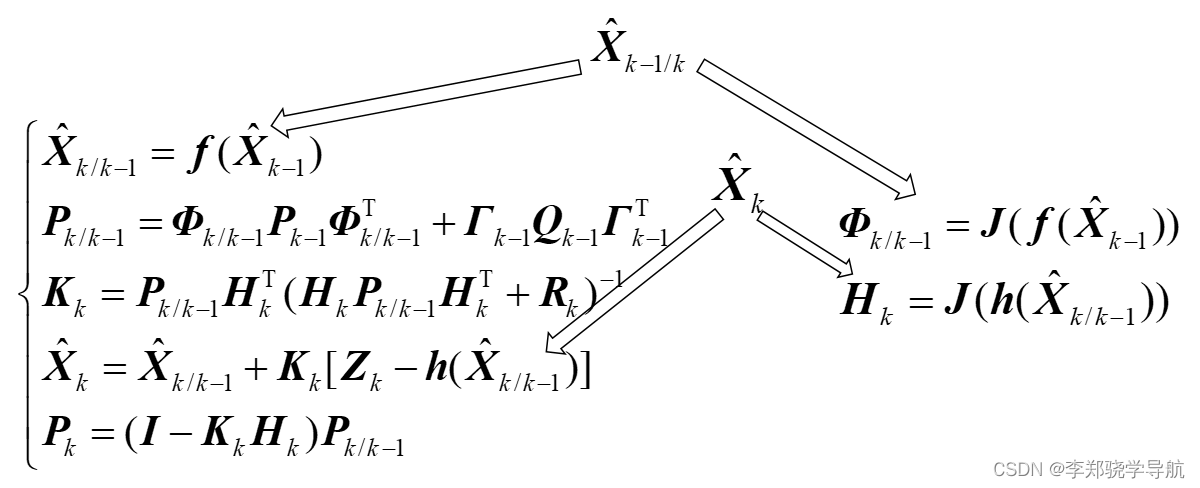
四、迭代EKF滤波
{ X ^ k / k − 1 = f ( X ^ k − 1 ) P k / k − 1 = Φ k / k − 1 P k − 1 Φ k / k − 1 T + Γ k − 1 Q k − 1 Γ k − 1 T Φ k / k − 1 = J ( f ( X ^ k − 1 ) ) K k = P k / k − 1 H k T ( H k P k / k − 1 H k T + R k ) − 1 H k = J ( h ( X ^ k / k − 1 ) ) X ^ k = X ^ k / k − 1 + K k [ Z k − h ( X ^ k / k − 1 ) ] P k = ( I − K k H k ) P k / k − 1 \left\{\begin{array}{ll}\hat{\boldsymbol{X}}_{k / k-1}=\boldsymbol{f}\left(\hat{\boldsymbol{X}}_{k-1}\right) & \\ \boldsymbol{P}_{k / k-1}={\color{red}\boldsymbol{\Phi}_{k / k-1}} \boldsymbol{P}_{k-1} {\color{red}\boldsymbol{\Phi}_{k / k-1}^{\mathrm{T}}}+\boldsymbol{\Gamma}_{k-1} \boldsymbol{Q}_{k-1} \boldsymbol{\Gamma}_{k-1}^{\mathrm{T}} & {\color{red}\boldsymbol{\Phi}_{k / k-1}=\boldsymbol{J}\left(\boldsymbol{f}\left(\hat{\boldsymbol{X}}_{k-1}\right)\right)} \\ \boldsymbol{K}_{k}=\boldsymbol{P}_{k / k-1} {\color{green}\boldsymbol{H}_{k}^{\mathrm{T}}}\left({\color{green}\boldsymbol{H}_{k}} \boldsymbol{P}_{k / k-1} {\color{green}\boldsymbol{H}_{k}^{\mathrm{T}}}+\boldsymbol{R}_{k}\right)^{-1} & {\color{green}\boldsymbol{H}_{k}=\boldsymbol{J}\left(\boldsymbol{h}\left(\hat{\boldsymbol{X}}_{k / k-1}\right)\right)} \\ \hat{\boldsymbol{X}}_{k}=\hat{\boldsymbol{X}}_{k / k-1}+\boldsymbol{K}_{k}\left[\boldsymbol{Z}_{k}-\boldsymbol{h}\left(\hat{\boldsymbol{X}}_{k / k-1}\right)\right] & \\ \boldsymbol{P}_{k}=\left(\boldsymbol{I}-\boldsymbol{K}_{k} {\color{green}\boldsymbol{H}_{k}}\right) \boldsymbol{P}_{k / k-1} & \end{array}\right. ⎩ ⎨ ⎧X^k/k−1=f(X^k−1)Pk/k−1=Φk/k−1Pk−1Φk/k−1T+Γk−1Qk−1Γk−1TKk=Pk/k−1HkT(HkPk/k−1HkT+Rk)−1X^k=X^k/k−1+Kk[Zk−h(X^k/k−1)]Pk=(I−KkHk)Pk/k−1Φk/k−1=J(f(X^k−1))Hk=J(h(X^k/k−1))
非线性系统展开点越接近你想研究的那个点,展开的精度越高。普通EKF的展开点是上一时刻 k − 1 k-1 k−1,考虑迭代修正展开点。做完一次滤波之后,有 k k k 时刻的新量测值,可以用新量测值对 k − 1 k-1 k−1 时刻做反向平滑,用反向平滑的值作为新的上一时刻的状态估计值,进行Kalman滤波。
预滤波:
{ X ^ k / k − 1 ∗ = f ( X ^ k − 1 ) P k / k − 1 ∗ = Φ k / k − 1 ∗ P k − 1 ( Φ k / k − 1 ∗ ) T + Γ k − 1 Q k − 1 Γ k − 1 T Φ k / k − 1 ∗ = J ( f ( X ^ k − 1 ) ) K k ∗ = P k / k − 1 ∗ ( H k ∗ ) T [ H k ∗ P k / k − 1 ∗ ( H k ∗ ) T + R k ] − 1 H k ∗ = J ( h ( X ^ k / k − 1 ∗ ) ) X ^ k ∗ = X ^ k / k − 1 ∗ + K k ∗ [ Z k − h ( X ^ k / k − 1 ∗ ) ] \left\{\begin{array}{ll} \hat{\boldsymbol{X}}_{k / k-1}^{*}=\boldsymbol{f}\left(\hat{\boldsymbol{X}}_{k-1}\right) \\ \boldsymbol{P}_{k / k-1}^{*}=\boldsymbol{\Phi}_{k / k-1}^{*} \boldsymbol{P}_{k-1}\left(\boldsymbol{\Phi}_{k / k-1}^{*}\right)^{\mathrm{T}}+\boldsymbol{\Gamma}_{k-1} \boldsymbol{Q}_{k-1} \boldsymbol{\Gamma}_{k-1}^{\mathrm{T}} & \boldsymbol{\Phi}_{k / k-1}^{*}=\boldsymbol{J}\left(\boldsymbol{f}\left(\hat{\boldsymbol{X}}_{k-1}\right)\right) \\ \boldsymbol{K}_{k}^{*}=\boldsymbol{P}_{k / k-1}^{*}\left(\boldsymbol{H}_{k}^{*}\right)^{\mathrm{T}}\left[\boldsymbol{H}_{k}^{*} \boldsymbol{P}_{k / k-1}^{*}\left(\boldsymbol{H}_{k}^{*}\right)^{\mathrm{T}}+\boldsymbol{R}_{k}\right]^{-1} & \boldsymbol{H}_{k}^{*}=\boldsymbol{J}\left(\boldsymbol{h}\left(\hat{\boldsymbol{X}}_{k / k-1}^{*}\right)\right) \\ \hat{\boldsymbol{X}}_{k}^{*}=\hat{\boldsymbol{X}}_{k / k-1}^{*}+\boldsymbol{K}_{k}^{*}\left[\boldsymbol{Z}_{k}-\boldsymbol{h}\left(\hat{\boldsymbol{X}}_{k / k-1}^{*}\right)\right] & \end{array}\right. ⎩ ⎨ ⎧X^k/k−1∗=f(X^k−1)Pk/k−1∗=Φk/k−1∗Pk−1(Φk/k−1∗)T+Γk−1Qk−1Γk−1TKk∗=Pk/k−1∗(Hk∗)T[Hk∗Pk/k−1∗(Hk∗)T+Rk]−1X^k∗=X^k/k−1∗+Kk∗[Zk−h(X^k/k−1∗)]Φk/k−1∗=J(f(X^k−1))Hk∗=J(h(X^k/k−1∗))
反向一步平滑:可以用RTS算法
X ^ k − 1 / k = X ^ k − 1 + P k − 1 ( Φ k / k − 1 ∗ ) T ( P k / k − 1 ∗ ) − 1 ( X ^ k ∗ − X ^ k / k − 1 ∗ ) \hat{\boldsymbol{X}}_{k-1 / k}=\hat{\boldsymbol{X}}_{k-1}+\boldsymbol{P}_{k-1}\left(\boldsymbol{\Phi}_{k / k-1}^{*}\right)^{\mathrm{T}}\left(\boldsymbol{P}_{k / k-1}^{*}\right)^{-1}\left(\hat{\boldsymbol{X}}_{k}^{*}-\hat{\boldsymbol{X}}_{k / k-1}^{*}\right) X^k−1/k=X^k−1+Pk−1(Φk/k−1∗)T(Pk/k−1∗)−1(X^k∗−X^k/k−1∗)
重做状态一步预测: X ^ k − 1 / k \hat{\boldsymbol{X}}_{k-1 / k} X^k−1/k 再做泰勒级数展开
X ^ k / k − 1 = f ( X ^ k − 1 ) = f ( X ^ k − 1 / k ) + f ( X ^ k − 1 ) − f ( X ^ k − 1 / k ) ≈ f ( X ^ k − 1 / k ) + J ( f ( X ^ k − 1 / k ) ) ( X ^ k − 1 − X ^ k − 1 / k ) \begin{aligned} \hat{\boldsymbol{X}}_{k / k-1} & =\boldsymbol{f}\left(\hat{\boldsymbol{X}}_{k-1}\right)=\boldsymbol{f}\left(\hat{\boldsymbol{X}}_{k-1 / k}\right)+\boldsymbol{f}\left(\hat{\boldsymbol{X}}_{k-1}\right)-\boldsymbol{f}\left(\hat{\boldsymbol{X}}_{k-1 / k}\right) \\ & \approx \boldsymbol{f}\left(\hat{\boldsymbol{X}}_{k-1 / k}\right)+\boldsymbol{J}\left(\boldsymbol{f}\left(\hat{\boldsymbol{X}}_{k-1 / k}\right)\right)\left(\hat{\boldsymbol{X}}_{k-1}-\hat{\boldsymbol{X}}_{k-1 / k}\right) \end{aligned} X^k/k−1=f(X^k−1)=f(X^k−1/k)+f(X^k−1)−f(X^k−1/k)≈f(X^k−1/k)+J(f(X^k−1/k))(X^k−1−X^k−1/k)
重做量测一步预测:
Z ^ k / k − 1 = h ( X ^ k / k − 1 ) = h ( X ^ k ∗ ) + h ( X ^ k / k − 1 ) − h ( X ^ k ∗ ) ≈ h ( X ^ k ∗ ) + J ( h ( X ^ k ∗ ) ) ( X ^ k / k − 1 − X ^ k ∗ ) \begin{aligned} \hat{\boldsymbol{Z}}_{k / k-1} & =\boldsymbol{h}\left(\hat{\boldsymbol{X}}_{k / k-1}\right)=\boldsymbol{h}\left(\hat{\boldsymbol{X}}_{k}^{*}\right)+\boldsymbol{h}\left(\hat{\boldsymbol{X}}_{k / k-1}\right)-\boldsymbol{h}\left(\hat{\boldsymbol{X}}_{k}^{*}\right) \\ & \approx \boldsymbol{h}\left(\hat{\boldsymbol{X}}_{k}^{*}\right)+\boldsymbol{J}\left(\boldsymbol{h}\left(\hat{\boldsymbol{X}}_{k}^{*}\right)\right)\left(\hat{\boldsymbol{X}}_{k / k-1}-\hat{\boldsymbol{X}}_{k}^{*}\right) \end{aligned} Z^k/k−1=h(X^k/k−1)=h(X^k∗)+h(X^k/k−1)−h(X^k∗)≈h(X^k∗)+J(h(X^k∗))(X^k/k−1−X^k∗)
迭代滤波:在此基础上做Kalman滤波
{ X ^ k / k − 1 = f ( X ^ k − 1 / k ) + Φ k / k − 1 ( X ^ k − 1 − X ^ k − 1 / k ) P k / k − 1 = Φ k / k − 1 P k − 1 Φ k / k − 1 T + Γ k − 1 Q k − 1 Γ k − 1 T Φ k / k − 1 = J ( f ( X ^ k − 1 / k ) ) K k = P k / k − 1 H k T ( H k P k / k − 1 H k T + R k ) − 1 H k = J ( h ( X ^ k ∗ ) ) X ^ k = X ^ k / k − 1 + K k [ Z k − h ( X ^ k ∗ ) − H k ( X ^ k / k − 1 − X ^ k ∗ ) ] P k = ( I − K k H k ) P k / k − 1 \left\{\begin{array}{ll} \hat{\boldsymbol{X}}_{k / k-1}=\boldsymbol{f}\left(\hat{\boldsymbol{X}}_{k-1 / k}\right)+\boldsymbol{\Phi}_{k / k-1}\left(\hat{\boldsymbol{X}}_{k-1}-\hat{\boldsymbol{X}}_{k-1 / k}\right) & \\ \boldsymbol{P}_{k / k-1}=\boldsymbol{\Phi}_{k / k-1} \boldsymbol{P}_{k-1} \boldsymbol{\Phi}_{k / k-1}^{\mathrm{T}}+\boldsymbol{\Gamma}_{k-1} \boldsymbol{Q}_{k-1} \boldsymbol{\Gamma}_{k-1}^{\mathrm{T}} & \boldsymbol{\Phi}_{k / k-1}=\boldsymbol{J}\left(\boldsymbol{f}\left(\hat{\boldsymbol{X}}_{k-1 / k}\right)\right) \\ \boldsymbol{K}_{k}=\boldsymbol{P}_{k / k-1} \boldsymbol{H}_{k}^{\mathrm{T}}\left(\boldsymbol{H}_{k} \boldsymbol{P}_{k / k-1} \boldsymbol{H}_{k}^{\mathrm{T}}+\boldsymbol{R}_{k}\right)^{-1} & \boldsymbol{H}_{k}=\boldsymbol{J}\left(\boldsymbol{h}\left(\hat{\boldsymbol{X}}_{k}^{*}\right)\right) \\ \hat{\boldsymbol{X}}_{k}=\hat{\boldsymbol{X}}_{k / k-1}+\boldsymbol{K}_{k}\left[\boldsymbol{Z}_{k}-\boldsymbol{h}\left(\hat{\boldsymbol{X}}_{k}^{*}\right)-\boldsymbol{H}_{k}\left(\hat{\boldsymbol{X}}_{k / k-1}-\hat{\boldsymbol{X}}_{k}^{*}\right)\right] \\ \boldsymbol{P}_{k}=\left(\boldsymbol{I}-\boldsymbol{K}_{k} \boldsymbol{H}_{k}\right) \boldsymbol{P}_{k / k-1} & \end{array}\right. ⎩ ⎨ ⎧X^k/k−1=f(X^k−1/k)+Φk/k−1(X^k−1−X^k−1/k)Pk/k−1=Φk/k−1Pk−1Φk/k−1T+Γk−1Qk−1Γk−1TKk=Pk/k−1HkT(HkPk/k−1HkT+Rk)−1X^k=X^k/k−1+Kk[Zk−h(X^k∗)−Hk(X^k/k−1−X^k∗)]Pk=(I−KkHk)Pk/k−1Φk/k−1=J(f(X^k−1/k))Hk=J(h(X^k∗))
还可以多次迭代,但收益小
相关文章:

卡尔曼滤波与组合导航原理(十二)扩展卡尔曼滤波:EKF、二阶EKF、迭代EKF
文章目录 一、多元向量的泰勒级数展开二、扩展Kalman滤波三、二阶滤波四、迭代EKF滤波 一、多元向量的泰勒级数展开 { y 1 f 1 ( X ) f 1 ( x 1 , x 2 , ⋯ x n ) y 2 f 2 ( X ) f 2 ( x 1 , x 2 , ⋯ x n ) ⋮ y m f m ( X ) f m ( x 1 , x 2 , ⋯ x n ) \left\{\begin{…...
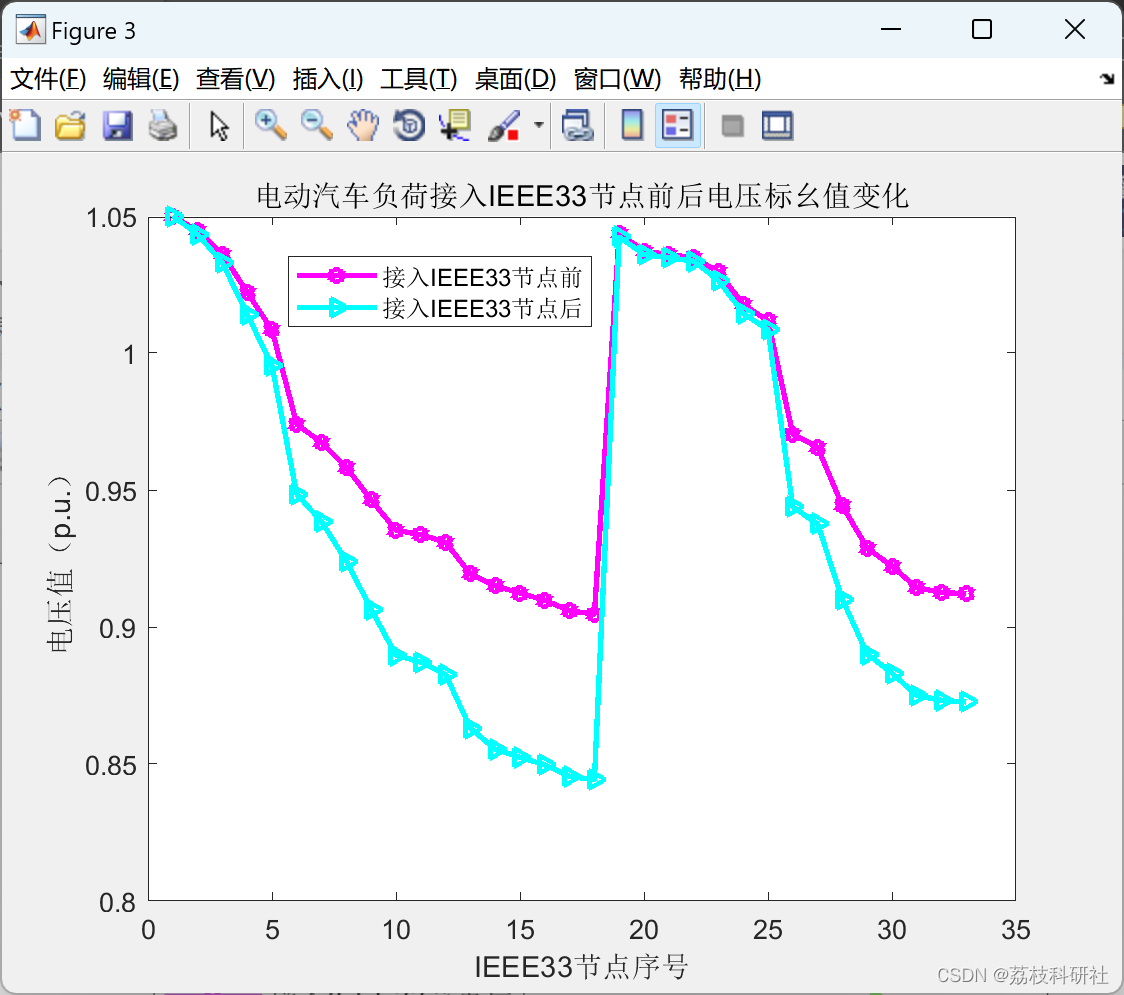
基于蒙特卡洛模拟法的电动汽车充电负荷研究(Matlab代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...
自学黑客【网络安全】,一般人我劝你还是算了吧
一、自学网络安全学习的误区和陷阱 1.不要试图先成为一名程序员(以编程为基础的学习)再开始学习 我在之前的回答中,我都一再强调不要以编程为基础再开始学习网络安全,一般来说,学习编程不但学习周期长,而…...

编程中的心理策略:如何从错误中学习并实现自我成长
在日复一日的工作中,我们免不了会产生一些失误,会因此感到沮丧和失望。但如何正确地对待和处理这些失误才是最重要的,它直接影响到我们的工作表现和个人成长。 一、面对失误而带来的指责和沮丧的策略 在程序设计领域,我们经常面临…...
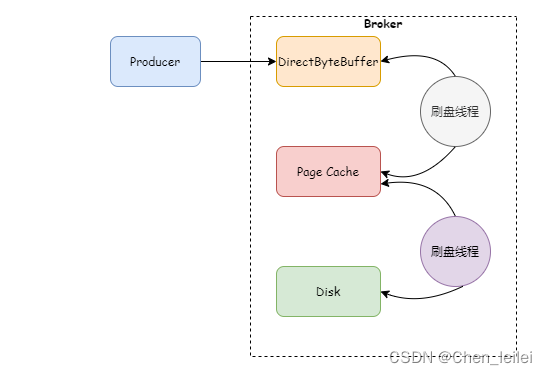
Rocket面试(五)Rocketmq发生流量控制的情况有哪些?
在使用rocketmq过程中总能看见一下异常 [TIMEOUT_CLEAN_QUEUE]broker busy, start flow control for a while, period in queue: 206ms, size of queue: 5这是因为Rocketmq出发了流量控制。 触发流量控制就是为了防止Broker压力过大挂掉。主要分为Broker流控,Consu…...

Tableau招聘信息数据可视化
获取的招聘信息数据为某招聘网站发布的大数据及数据分析相关岗位,对其他计算机相关岗位的招聘信息数据分析也有一定的参考价值。因为所获取的招聘信息数据数量只有1万左右,实际的招聘信息数量肯定不止1万,所以可能会与实际信息有一定的误差。…...
:合理应对异常)
游戏服务器开发指南(八):合理应对异常
大家好!我是长三月,一位在游戏行业工作多年的老程序员,专注于分享服务器开发相关的文章。 本文是通用程序设计主题下的第二篇。这个主题主要探讨如何编写高效、健壮、易读的游戏业务代码,每篇从一个小点切入。本次讨论的要点是&a…...

【g】聚类算法之K-means算法
聚类算法是一种无监督学习方法,它将相似的数据样本划分为一组,同时将不相似的数据样本划分为另一组。这个过程由计算机自动完成,不需要任何人为的干预。 K-means算法是一种经典的聚类算法,它的主要思想是把数据集分成k个簇&#…...
scala内建控制结构
一、条件表达式 (一)语法格式 - if (条件) 值1 else 值2(二)执行情况 条件为真,结果是值1;条件为假,结果是值2。如果if和else的返回结果同为某种类型,那么条件表达式结果也是那种类…...

Linux SSH命令实战教程,提升你的服务器管理基本功!
前言 大家好,又见面了,我是沐风晓月,本文是专栏【linux基本功-基础命令实战】的第62篇文章。 专栏地址:[linux基本功-基础命令专栏] , 此专栏是沐风晓月对Linux常用命令的汇总,希望能够加深自己的印象&am…...
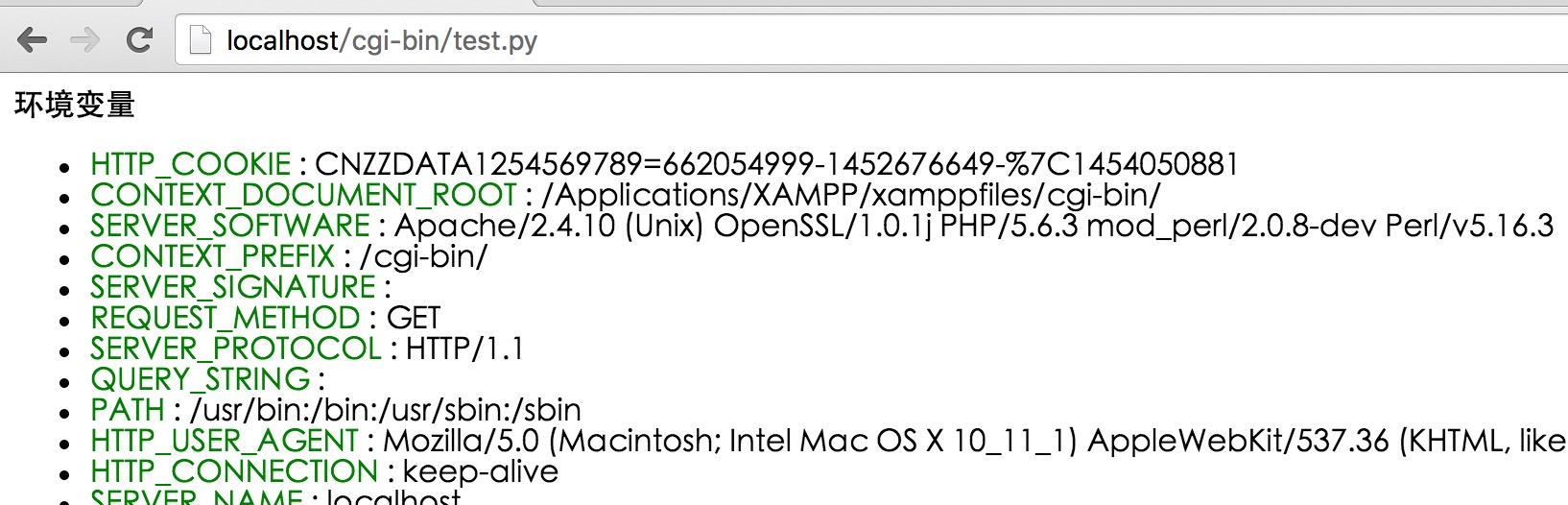
【Python】Python进阶系列教程-- Python3 CGI编程(二)
文章目录 前言什么是CGI网页浏览CGI架构图Web服务器支持及配置第一个CGI程序HTTP头部CGI环境变量GET和POST方法使用GET方法传输数据简单的表单实例:GET方法使用POST方法传递数据通过CGI程序传递checkbox数据通过CGI程序传递Radio数据通过CGI程序传递 Textarea 数据通…...

do..while、while、for循环反汇编剖析
1、循环语句重要特征提取 循环语句最重要的特点就是执行的过程中会往上跳!!! 箭头往上跳的一般都是循环语句,比如下面的for循环: 2、do..while语句反汇编 #include<iostream> using namespace std; #pragma …...

【代码随想录】刷题Day53
1.最长公共子序列 1143. 最长公共子序列 和之前的一道题目的区别就是这个子序列不需要每个字符相邻。那么条件就变成两种了,一种是当前的字符相同,一种是不同。相同跟之前的条件一样;不同则需要继承上次比较的较大值。if (text1[i - 1] tex…...

MySQL 索引及查询优化总结
一个简单的对比测试 前面的案例中,c2c_zwdb.t_file_count表只有一个自增id,FFileName字段未加索引的sql执行情况如下: 在上图中,typeall,keynull,rows33777。该sql未使用索引,是一个效率非常低…...
什么是AJAX?
AJAX是一种基于Web的技术,它允许Web应用程序在不刷新整个页面的情况下与服务器进行交互。通过AJAX,Web应用程序可以使用JavaScript向服务器发送异步请求并在不干扰用户的情况下更新页面的部分内容。 AJAX是Asynchronous JavaScript and XML的缩写。尽管…...

报表生成器FastReport .Net用户指南:显示数据列、HTML标签
FastReport .Net是一款全功能的Windows Forms、ASP.NET和MVC报表分析解决方案,使用FastReport .NET可以创建独立于应用程序的.NET报表,同时FastReport .Net支持中文、英语等14种语言,可以让你的产品保证真正的国际性。 FastReport.NET官方版…...

bootstrap-dialog弹框,去掉遮盖层,可移动
1.去掉遮盖层的设置data-backdrop"false" <div class"modal fade" id"modal" aria-modal"true" role"dialog" data-backdrop"false" style"width:50%"><div class"modal-dialog modal-l…...

7. user-Agent破解反爬机制
文章目录 1. 为什么要设置反爬机制2. 服务器如何区分浏览器访问和爬虫访问3. 反爬虫机制4. User-Agent是什么5. 如何查询网页的User-Agent6. user-agent信息解析7. 爬虫程序user-agent和浏览器user-agent的区别8. 代码查看爬虫程序的user-agent9. 在代码中加入请求头信息 1. 为…...

3.Nginx+Tomcat负载均衡和动静分离群集
文章目录 NginxTomcat负载均衡和动静分离群集Nginx作用实验七层反向代理nginx动静分离四层反向代理负载均衡 NginxTomcat负载均衡和动静分离群集 Nginx是-款非常优秀的HTTP服务器软件 支持高达50 000个并发连接数的响应拥有强大的静态资源处理能力运行稳定内存、CPU等系统资源…...
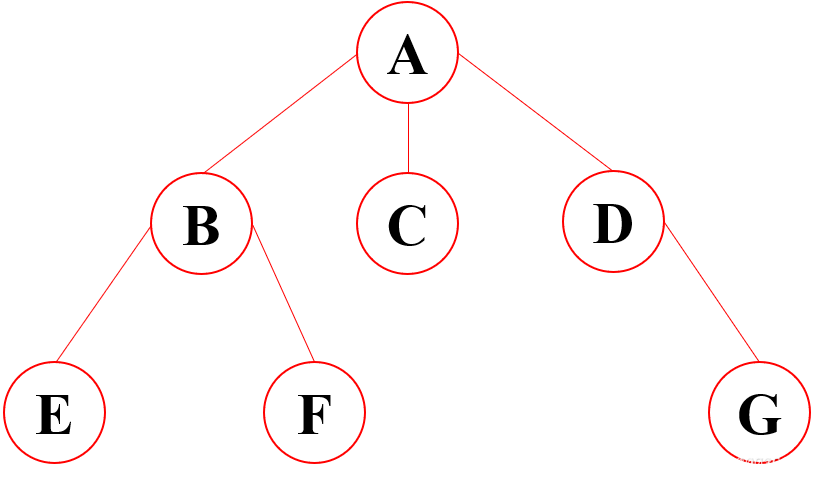
数据结构与算法之树结构
目录 为什么要使用树结构树结构基本概念树的种类树的存储与表示常见的一些树的应用场景为什么要使用树结构 线性结构中不论是数组还是链表,他们都存在着诟病;比如查找某个数必须从头开始查,消耗较多的时间。使用树结构,在插入和查找的性能上相对都会比线性结构要好 树结构…...

Vim 调用外部命令学习笔记
Vim 外部命令集成完全指南 文章目录 Vim 外部命令集成完全指南核心概念理解命令语法解析语法对比 常用外部命令详解文本排序与去重文本筛选与搜索高级 grep 搜索技巧文本替换与编辑字符处理高级文本处理编程语言处理其他实用命令 范围操作示例指定行范围处理复合命令示例 实用技…...

日语AI面试高效通关秘籍:专业解读与青柚面试智能助攻
在如今就业市场竞争日益激烈的背景下,越来越多的求职者将目光投向了日本及中日双语岗位。但是,一场日语面试往往让许多人感到步履维艰。你是否也曾因为面试官抛出的“刁钻问题”而心生畏惧?面对生疏的日语交流环境,即便提前恶补了…...

基于FPGA的PID算法学习———实现PID比例控制算法
基于FPGA的PID算法学习 前言一、PID算法分析二、PID仿真分析1. PID代码2.PI代码3.P代码4.顶层5.测试文件6.仿真波形 总结 前言 学习内容:参考网站: PID算法控制 PID即:Proportional(比例)、Integral(积分&…...

【力扣数据库知识手册笔记】索引
索引 索引的优缺点 优点1. 通过创建唯一性索引,可以保证数据库表中每一行数据的唯一性。2. 可以加快数据的检索速度(创建索引的主要原因)。3. 可以加速表和表之间的连接,实现数据的参考完整性。4. 可以在查询过程中,…...

阿里云ACP云计算备考笔记 (5)——弹性伸缩
目录 第一章 概述 第二章 弹性伸缩简介 1、弹性伸缩 2、垂直伸缩 3、优势 4、应用场景 ① 无规律的业务量波动 ② 有规律的业务量波动 ③ 无明显业务量波动 ④ 混合型业务 ⑤ 消息通知 ⑥ 生命周期挂钩 ⑦ 自定义方式 ⑧ 滚的升级 5、使用限制 第三章 主要定义 …...

TRS收益互换:跨境资本流动的金融创新工具与系统化解决方案
一、TRS收益互换的本质与业务逻辑 (一)概念解析 TRS(Total Return Swap)收益互换是一种金融衍生工具,指交易双方约定在未来一定期限内,基于特定资产或指数的表现进行现金流交换的协议。其核心特征包括&am…...
)
Java入门学习详细版(一)
大家好,Java 学习是一个系统学习的过程,核心原则就是“理论 实践 坚持”,并且需循序渐进,不可过于着急,本篇文章推出的这份详细入门学习资料将带大家从零基础开始,逐步掌握 Java 的核心概念和编程技能。 …...

select、poll、epoll 与 Reactor 模式
在高并发网络编程领域,高效处理大量连接和 I/O 事件是系统性能的关键。select、poll、epoll 作为 I/O 多路复用技术的代表,以及基于它们实现的 Reactor 模式,为开发者提供了强大的工具。本文将深入探讨这些技术的底层原理、优缺点。 一、I…...

【Oracle】分区表
个人主页:Guiat 归属专栏:Oracle 文章目录 1. 分区表基础概述1.1 分区表的概念与优势1.2 分区类型概览1.3 分区表的工作原理 2. 范围分区 (RANGE Partitioning)2.1 基础范围分区2.1.1 按日期范围分区2.1.2 按数值范围分区 2.2 间隔分区 (INTERVAL Partit…...

CMake控制VS2022项目文件分组
我们可以通过 CMake 控制源文件的组织结构,使它们在 VS 解决方案资源管理器中以“组”(Filter)的形式进行分类展示。 🎯 目标 通过 CMake 脚本将 .cpp、.h 等源文件分组显示在 Visual Studio 2022 的解决方案资源管理器中。 ✅ 支持的方法汇总(共4种) 方法描述是否推荐…...
