三十六、数学知识——组合数(递推法 + 预处理法 + 卢卡斯定理 + 分解质因数求解组合数 + 卡特兰数)
组合数算法主要内容
- 一、基本思路
- 1、组合数基本概念
- 2、递推法——询问次数多 + a b 值较小 + 模处理(%mod)
- 3、预处理阶乘方法——询问次数较多 + a b 值很大 + 模处理(%mod)
- 4、卢卡斯定理——询问次数较少 + (a b 值很大) + mod模也很大
- 5、分解质因数法(无模直接求解)——没有模运算 + 大数运算求解
- 6、卡特兰数——多问题可转化为此问题 + 组合数求解
- 二、Java、C语言模板实现
- 三、例题题解
一、基本思路
1、组合数基本概念
- 组合数:排列组合中的组合数,即给了a个人,从中选b个,问有多少种排列方方式: C b a C\begin{matrix} b \\ a \end{matrix} Cba
- 公式如下:

2、递推法——询问次数多 + a b 值较小 + 模处理(%mod)
- 使用条件:
-
- 1 - 10万组询问
-
- 1 ≤ b ≤ a ≤ 2000
- 公式如下:

- 如何理解:
-
-
- 在进行选择的时候,包含需要的的一个(已选一个) C b − 1 a − 1 C\begin{matrix} b-1 \\ a-1 \end{matrix} Cb−1a−1
-
-
-
- 在进行选择的时候,不包含需要选的那个(1个未选) C b a − 1 C\begin{matrix} b \\ a-1\end{matrix} Cba−1
-
-
- 两种情况相加即为递推公式,即为所需内容。
3、预处理阶乘方法——询问次数较多 + a b 值很大 + 模处理(%mod)
- 条件:
-
- 1万次问询
-
- 1 ≤ b ≤ a ≤ 10^5
- 公式:

- 分部求解:
-
- a!阶乘求解 :

-
- 1/((a-b)! * b!):
-
- 已知:

- 已知:
-
- 求解:

-
- 注意此处如果 mod 是质数则可以使用快速幂进行逆元求解,不是质数则需要使用扩展欧几里得算法进行逆元求解。
-
- 组合求解:

- 总结:

4、卢卡斯定理——询问次数较少 + (a b 值很大) + mod模也很大
- 条件:
-
- 20次询问;
-
- 1 ≤ b ≤ a ≤ 10^18
-
- 1 ≤ p ≤ 10^5
- 定理:

- 推导过程:(说实话没看懂,感觉可以直接背过模板进行计算)

5、分解质因数法(无模直接求解)——没有模运算 + 大数运算求解
- 公式:

- 原理——分解质因数 + 大数运算求解

-
步骤:
-
当我们需要求出组合数的真实值,而非对某个数的余数时,分解质因数的方式比较好用:
- 筛法求出范围内的所有质数
- 通过 C(a, b) = a! / b! / (a - b)! 这个公式求出每个质因子的次数。 n! 中p的次数是 n / p + n / p^2 + n / p^3 + …
- 用高精度乘法将所有质因子相乘
-
注意:说实话没怎么看懂,我还是背模板吧
6、卡特兰数——多问题可转化为此问题 + 组合数求解
- 卡特兰数简介:
- 卡特兰数是组合数学中一个常出现于各种计数问题中的数列。以中国蒙古族数学家明安图和比利时的数学家欧仁·查理·卡特兰的名字来命名,其前几项为(从第0项开始):1, 1, 2, 5, 14, 42, 132, 429, 1430, 4862, 16796, 58786, 208012, 742900, 2674440, 9694845, 35357670, 129644790, 477638700, 1767263190, 6564120420, 24466267020, 91482563640, 343059613650, 1289904147324, 4861946401452, …

- 卡特兰数结论:

- 卡特兰数推导(来自csdn作者:你好世界wxx):
-
- 首先我们需要将上述问题转换成一个等价的问题:在一个二维平面内,从(0, 0)出发到达(n, n),每次可以向上或者向右走一格,0代表向右走一个,1代表向上走一格,则每条路径都会代表一个01序列,则满足任意前缀中0的个数不少于1个数序列对应的路径则右下侧,如下图:

-
- 符合要求的路径必须严格在上图中红色线的下面(不可以碰到图中的红线,可以碰到绿线)。则我们考虑任意一条不合法路径,例如下图:


-
- 补充:

- 举例:
- 给定 n 个 0和 n 个 1,它们将按照某种顺序排成长度为 2n 的序列,求它们能排列成的所有序列中,能够满足任意前缀序列中 0的个数都不少于 1 的个数的序列有多少个。输出的答案对 10^9+7取模。


- 注意:
-
- mod为质数进行逆元求解:快速幂
-
- mod非质数求解逆元:扩展欧几里得算法
二、Java、C语言模板实现
- 递推法:
// java 模板
static long[][] c = new long[N][N];static void init(){ // 直接进行预处理,不用每次进行产生,就会减小时间复杂度for(int i = 0; i < N; i++){for(int j = 0; j <= i; j++){if(j == 0){c[i][j] = 1;}else{c[i][j] = (c[i - 1][j] + c[i - 1][j - 1]) % Mod; // c[i][j]实际上i是底数,j是选取的数,即 i = a, j = b;}}}}
- 预处理方法:
// java 模板
static int mod = (int)(1e9 + 7);
static long[] fact = new long[N]; // 使用 long 是为了防止爆 int
static long[] infact = new long[N];static long qmi(long a, long k, long p){ // 快速幂求解逆元,其中k = mod - 2 使用费马定理求解逆元long res = 1; while((k != 0)){if((k & 1) == 1){res = res * a % p;}k >>= 1;a = a * a % p;} return res;}static void init(){ // 对fact[] infact[] 两个数组进行预处理,后面只需要简单计算即可以求出 fact[0] = 1;infact[0] = 1;for(int i = 1; i < N; i++){fact[i] = fact[i - 1] * i % mod; // a! 阶乘求解infact[i] = infact[i - 1] * qmi(i, mod - 2, mod) % mod; // 1/(b!) 阶乘倒数求解}}// 组合数求解
long result = (fact[a] * infact[b] % mod) * infact[a - b] % mod;
- 卢卡斯定理:
// java 模板
static long p;static long qmi(long a, long k){ // 快速幂求解long res = 1;while(k != 0){if((k & 1) == 1){res = res * a % p;} k >>=1;a = a * a % p;}return res;}static long C(long a, long b){
// 计算Cab,用的是预处理阶乘的方法————此处后面还会常用,一定要熟记,是进行Cab求解重要方法long res = 1;for(long i = 1,j = a; i <= b; i++,j--){res = res * j % p;res = res * qmi(i , p - 2)% p; // qmi快速幂进行其中的逆元求解}return res;
}static long lucas(long a, long b){ // 卢卡斯定理求解 Cabif(a < p && b < p){return C(a, b); // 不需要进行模处理,直接就可以计算}return C(a % p, b % p) * lucas(a/p, b/p) % p; // 卢卡斯公式
}- 分解质因数法(无模直接求解):
// java 模板
static int[] sum = new int[N];
static int[] primes = new int[N];
static boolean[] st = new boolean[N];
static int cnt;//线性筛筛质数
static void get_primes(int x){for(int i=2; i<=x; i++){if(!st[i]) primes[cnt++] = i;for(int j=0; primes[j]<=x/i; j++){st[primes[j]*i] = true;if(i%primes[j]==0) break;}}
}//获得n!中某个质数的个数
static int get(int n, int p){int res = 0;while(n!=0){res+=n/p;n/=p;}return res;
}// 主函数
get_primes(a);
for(int i=0; i<cnt; i++){int p = primes[i];sum[i] = get(a, p) - get(b, p) - get(a-b, p); // 最终得到质数个数
}BigInteger res = new BigInteger("1"); // 大数
for(int i=0; i < cnt; i++){ // 质数个数int p = primes[i];for(int j=0; j<sum[i]; j++){res = res.multiply(new BigInteger(String.valueOf(p))); // 阶乘求解}
}- 卡特兰数:
// Java模板
static long qmi(long a, long k){ // 快速幂求解质数逆元long res = 1;while(k != 0){if((k & 1) == 1){res = res * a % mod;} k >>= 1;a = a * a % mod;} return res;}static long C(long a, long b){
// 此处求解 ab 范围不是很大的————组合数 % mod
// 假如ab范围更大的话,则需要使用卢卡斯定理long res = 1;for(long i = 1, j = a; i <= b;i++, j--){res = res * j % mod;res = res * qmi(i , mod - 2) % mod;}return res;}// 主函数
// !!!!!!可以用逆元来表示 (1/(n + 1)!)
long result = C(2 * n, n) * qmi(n + 1, mod - 2) % mod ; // 此处用逆元来表示(1/(n + 1)!)
- 扩展欧几里得算法:
import java.util.*;
public class Main{static int m = (int) 1e9 + 7;public static int exgcd(int a,int b,int[] x,int[] y){ // 扩展欧几里得算法if(b == 0){x[0] = 1; y[0] = 0;return a;}int d = exgcd(b,a % b,y,x);y[0] -= (a / b) * x[0] % m;return d;}public static void main(String[] args){Scanner scan = new Scanner(System.in);int n = scan.nextInt();//卡特兰数公式;c[2n][n] - c[2n][n-1] = c[2n][n] / ( n + 1)int a = 2 * n;int b = n;int[] x = new int[1];int[] y = new int[1];long res = 1;for(int i = a ;i > a - b; i --) res = res * i % m;for(int i = 1 ; i <= n ; i ++ ){exgcd(i,m,x,y);res =( res * x[0] % m + m )% m;//同下}exgcd(n + 1, m,x,y);//这里是因为有可能x[0]是系数所以有可能是负数,所以模之后在加上一个m在模,就可以得到正res = (res * x[0] % m + m) % m;System.out.println(res);}
}- C++模板
// C++ 模板,由yxc实现
1、递推法求组合数 —— 模板题 AcWing 885. 求组合数 I
// c[a][b] 表示从a个苹果中选b个的方案数
for (int i = 0; i < N; i ++ )for (int j = 0; j <= i; j ++ )if (!j) c[i][j] = 1;else c[i][j] = (c[i - 1][j] + c[i - 1][j - 1]) % mod;2、通过预处理逆元的方式求组合数 —— 模板题 AcWing 886. 求组合数 II
首先预处理出所有阶乘取模的余数fact[N],以及所有阶乘取模的逆元infact[N]
如果取模的数是质数,可以用费马小定理求逆元
int qmi(int a, int k, int p) // 快速幂模板
{int res = 1;while (k){if (k & 1) res = (LL)res * a % p;a = (LL)a * a % p;k >>= 1;}return res;
}// 预处理阶乘的余数和阶乘逆元的余数
fact[0] = infact[0] = 1;
for (int i = 1; i < N; i ++ )
{fact[i] = (LL)fact[i - 1] * i % mod;infact[i] = (LL)infact[i - 1] * qmi(i, mod - 2, mod) % mod;
}3、Lucas定理 —— 模板题 AcWing 887. 求组合数 III
若p是质数,则对于任意整数 1 <= m <= n,有:C(n, m) = C(n % p, m % p) * C(n / p, m / p) (mod p)int qmi(int a, int k, int p) // 快速幂模板
{int res = 1 % p;while (k){if (k & 1) res = (LL)res * a % p;a = (LL)a * a % p;k >>= 1;}return res;
}int C(int a, int b, int p) // 通过定理求组合数C(a, b)
{if (a < b) return 0;LL x = 1, y = 1; // x是分子,y是分母for (int i = a, j = 1; j <= b; i --, j ++ ){x = (LL)x * i % p;y = (LL) y * j % p;}return x * (LL)qmi(y, p - 2, p) % p;
}int lucas(LL a, LL b, int p)
{if (a < p && b < p) return C(a, b, p);return (LL)C(a % p, b % p, p) * lucas(a / p, b / p, p) % p;
}4、分解质因数法求组合数 —— 模板题 AcWing 888. 求组合数 IV
当我们需要求出组合数的真实值,而非对某个数的余数时,分解质因数的方式比较好用:1. 筛法求出范围内的所有质数2. 通过 C(a, b) = a! / b! / (a - b)! 这个公式求出每个质因子的次数。 n! 中p的次数是 n / p + n / p^2 + n / p^3 + ...3. 用高精度乘法将所有质因子相乘int primes[N], cnt; // 存储所有质数
int sum[N]; // 存储每个质数的次数
bool st[N]; // 存储每个数是否已被筛掉void get_primes(int n) // 线性筛法求素数
{for (int i = 2; i <= n; i ++ ){if (!st[i]) primes[cnt ++ ] = i;for (int j = 0; primes[j] <= n / i; j ++ ){st[primes[j] * i] = true;if (i % primes[j] == 0) break;}}
}int get(int n, int p) // 求n!中的次数
{int res = 0;while (n){res += n / p;n /= p;}return res;
}vector<int> mul(vector<int> a, int b) // 高精度乘低精度模板
{vector<int> c;int t = 0;for (int i = 0; i < a.size(); i ++ ){t += a[i] * b;c.push_back(t % 10);t /= 10;}while (t){c.push_back(t % 10);t /= 10;}return c;
}get_primes(a); // 预处理范围内的所有质数for (int i = 0; i < cnt; i ++ ) // 求每个质因数的次数
{int p = primes[i];sum[i] = get(a, p) - get(b, p) - get(a - b, p);
}vector<int> res;
res.push_back(1);for (int i = 0; i < cnt; i ++ ) // 用高精度乘法将所有质因子相乘for (int j = 0; j < sum[i]; j ++ )res = mul(res, primes[i]);5、卡特兰数 —— 模板题 AcWing 889. 满足条件的01序列
给定n个0和n个1,它们按照某种顺序排成长度为2n的序列,满足任意前缀中0的个数都不少于1的个数的序列的数量为: Cat(n) = C(2n, n) / (n + 1)
三、例题题解

// java题解实现
// 递推法
import java.util.*;
import java.io.*;
public class Main{static int Mod = (int)(1e9 + 7); // 此处的高次方值+7要用括号括起来static int N = 2010;static long[][] c = new long[N][N];static void init(){ // 直接进行预处理,不用每次进行产生,就会减小时间复杂度for(int i = 0; i < N; i++){for(int j = 0; j <= i; j++){if(j == 0){c[i][j] = 1;}else{c[i][j] = (c[i - 1][j] + c[i - 1][j - 1]) % Mod; // c[i][j]实际上i是底数,j是选取的数}}}}public static void main(String[] args) throws IOException {init();BufferedReader in = new BufferedReader(new InputStreamReader(System.in));String str1 = in.readLine();int n = Integer.parseInt(str1);for(int i = 0; i < n; i++){String[] str2 = in.readLine().split(" ");int a = Integer.parseInt(str2[0]);int b = Integer.parseInt(str2[1]);System.out.println(c[a][b]);}}
}
// 预处理方法求解组合数
import java.util.*;
import java.io.*;public class Main{static int N = 100010; // 数据比较大使用此方法static int mod = (int)(1e9 + 7);static long[] fact = new long[N]; // 使用 long 是为了防止爆 intstatic long[] infact = new long[N];static long qmi(long a, long k, long p){ // 快速幂求解逆元,其中k = mod - 2 使用费马定理求解逆元long res = 1;while((k != 0)){if((k & 1) == 1){res = res * a % p;}k >>= 1;a = a * a % p;}return res;}static void init(){ // 对fact[] infact[] 两个数组进行预处理,后面只需要简单计算即可以求出 fact[0] = 1;infact[0] = 1;for(int i = 1; i < N; i++){fact[i] = fact[i - 1] * i % mod; // a! 阶乘求解infact[i] = infact[i - 1] * qmi(i, mod - 2, mod) % mod; // 1/(b!) 阶乘倒数求解}}public static void main(String[] args) throws IOException {BufferedReader in = new BufferedReader(new InputStreamReader(System.in));String str1 = in.readLine();int n = Integer.parseInt(str1);init(); // 预处理阶乘数组while(n-- != 0){String[] str2 = in.readLine().split(" ");int a = Integer.parseInt(str2[0]);int b = Integer.parseInt(str2[1]);System.out.println((fact[a] * infact[b] % mod) * infact[a - b] % mod); // 组合数求解,组合数公式得来}}
}
// 卢卡斯定理需要解决的问题:
// 1、问询次数很小
// 2、组合数中的a,b,p范围很大
import java.util.*;
import java.io.*;public class Main{static long p;static long qmi(long a, long k){ // 快速幂求解long res = 1;while(k != 0){if((k & 1) == 1){res = res * a % p;}k >>=1;a = a * a % p;}return res;}static long C(long a, long b){ // 计算Cab,用的是预处理阶乘的方法long res = 1;for(long i = 1,j = a; i <= b; i++,j--){res = res * j % p;res = res * qmi(i , p - 2)% p; // qmi快速幂进行其中的逆元求解}return res;}static long lucas(long a, long b){ // 卢卡斯定理if(a < p && b < p){return C(a, b); // 不需要进行模处理,直接就可以计算}return C(a % p, b % p) * lucas(a/p, b/p) % p; // 卢卡斯公式}public static void main(String[] args) throws IOException {BufferedReader in = new BufferedReader(new InputStreamReader(System.in));String str1 = in.readLine();int n = Integer.parseInt(str1);while(n-- != 0){String[] str2 = in.readLine().split(" ");long a = Long.parseLong(str2[0]); // 此处是将String转换成long类型long b = Long.parseLong(str2[1]);p = Long.parseLong(str2[2]);System.out.println(lucas(a, b));}}
}
// 分解质因数求解
import java.io.*;
import java.math.BigInteger;
import java.util.*;class Main{static int N = 100010;static int[] sum = new int[N];static int[] primes = new int[N];static boolean[] st = new boolean[N];static int cnt;//线性筛筛质数static void get_primes(int x){for(int i=2; i<=x; i++){if(!st[i]) primes[cnt++] = i;for(int j=0; primes[j]<=x/i; j++){st[primes[j]*i] = true;if(i%primes[j]==0) break;}}}//获得n!中某个质数的个数static int get(int n, int p){int res = 0;while(n!=0){res+=n/p;n/=p;}return res;}public static void main(String[]args)throws IOException{BufferedReader in=new BufferedReader(new InputStreamReader(System.in));String[]arr=in.readLine().split(" ");int a=Integer.parseInt(arr[0]);int b=Integer.parseInt(arr[1]);get_primes(a);for(int i=0; i<cnt; i++){int p = primes[i];sum[i] = get(a, p) - get(b, p) - get(a-b, p); // 最终得到质数个数}BigInteger res = new BigInteger("1"); // 大数for(int i=0; i < cnt; i++){ // 质数个数int p = primes[i];for(int j=0; j<sum[i]; j++){res = res.multiply(new BigInteger(String.valueOf(p))); // 阶乘求解}}System.out.println(res);}
}
// 卡特兰数求解
import java.util.*;
import java.io.*;public class Main{static int mod = (int)(1e9 + 7);static long qmi(long a, long k){ // 快速幂求解质数逆元long res = 1;while(k != 0){if((k & 1) == 1){res = res * a % mod;}k >>= 1;a = a * a % mod;}return res;}static long C(long a, long b){ // 此处求解 ab 范围不是很大的————组合数 % mod// 假如ab范围更大的话,则需要使用卢卡斯定理long res = 1;for(long i = 1, j = a; i <= b;i++, j--){res = res * j % mod;res = res * qmi(i , mod - 2) % mod;}return res;}public static void main(String[] args) throws IOException {BufferedReader in = new BufferedReader(new InputStreamReader(System.in));int n = Integer.parseInt(in.readLine());long result = C(2 * n, n) * qmi(n + 1, mod - 2) % mod ; // 此处用逆元来表示(1/(n + 1))System.out.println(result);}
}
相关文章:

三十六、数学知识——组合数(递推法 + 预处理法 + 卢卡斯定理 + 分解质因数求解组合数 + 卡特兰数)
组合数算法主要内容 一、基本思路1、组合数基本概念2、递推法——询问次数多 a b 值较小 模处理(%mod)3、预处理阶乘方法——询问次数较多 a b 值很大 模处理(%mod)4、卢卡斯定理——询问次数较少 (a b 值很大&am…...

LinuxC编程——高级文件操作
目录 一、查询文件信息1、stat2、stat fstat lstat区别 二、目录操作2.1 opendir2.2 readdir2.3 closedir例练习:实现ls操作 三、库3.1 库的定义3.2 库的分类3.2.1 静态库3.2.2 动态库 3.3 创建库3.3.1 静态库制作3.3.2 动态库制作 一、查询文件信息 1、stat int …...
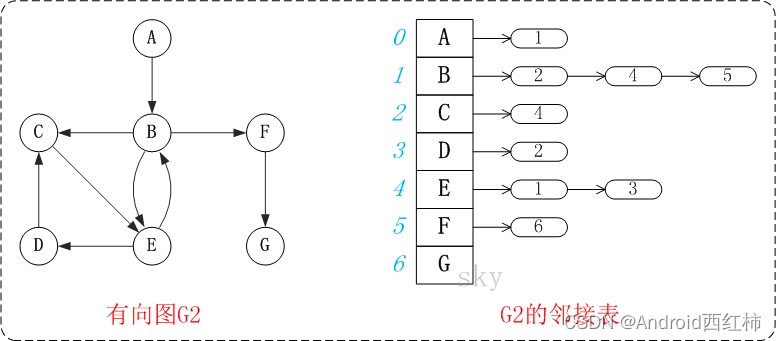
【基础知识整理】图的基本概念 邻接矩阵 邻接表
一、图概述 定义: 图(graph)是由一些点(vertex)和这些点之间的连线(edge)所组成的; 其中,点通常被成为"顶点(vertex)“,而点与点之间的连线则被成为"边或弧”(edege)。 通常记为,G(V,E)。 图是一种重要的…...

5.程序控制结构|Java学习笔记
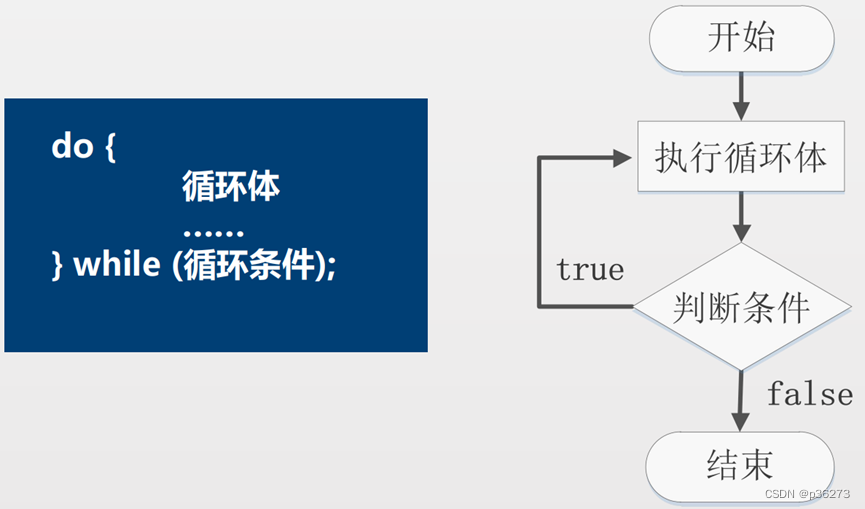
文章目录 程序流程控制介绍顺序控制分支控制分支控制if elseswitch分支结构 循环控制for循环控制while循环控制do...while循环控制跳转控制语句breakcontinuereturn 程序流程控制介绍 顺序控制分支控制循环控制 顺序控制 程序从上到下逐行地执行,中间没有任何判断…...
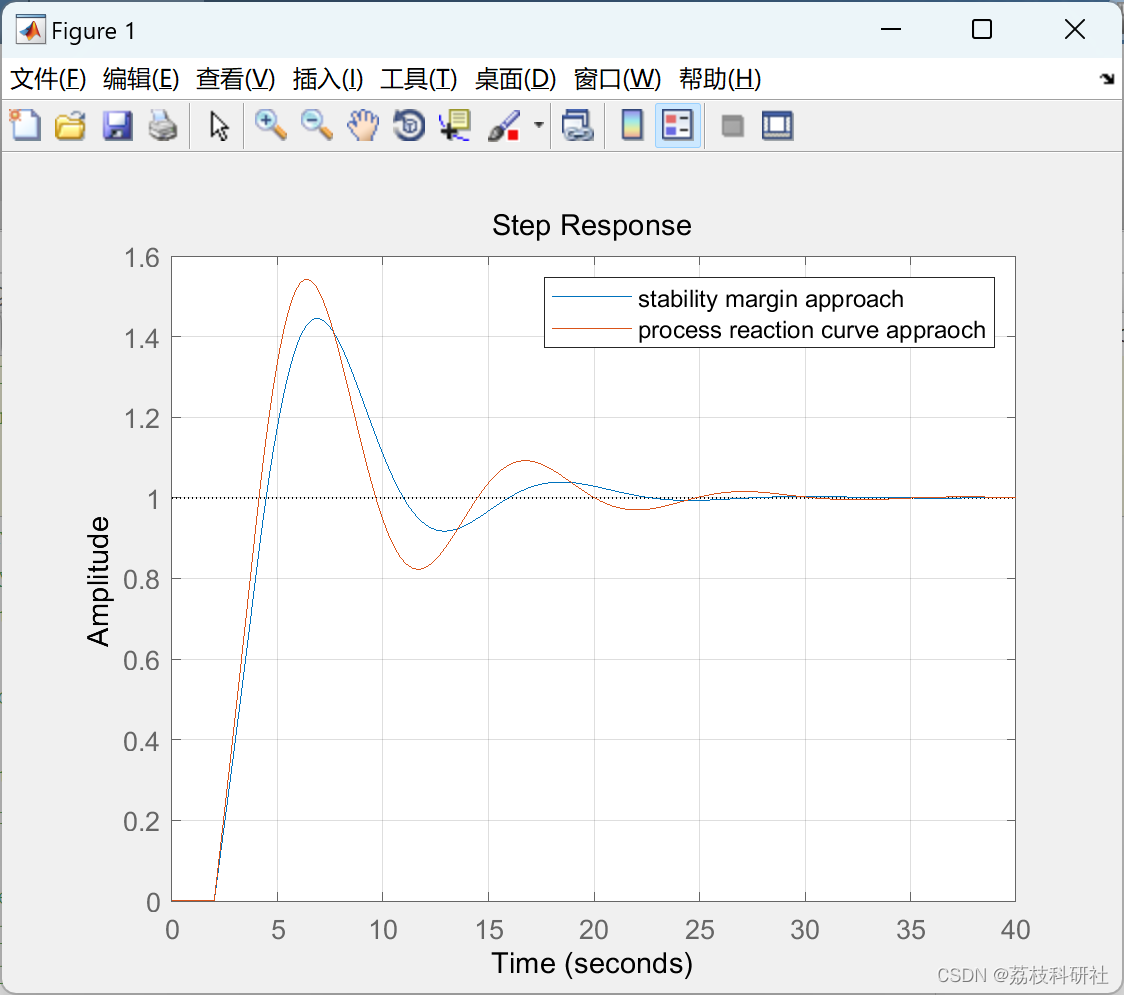
【最优PID 整定】PID性能指标(ISE,IAE,ITSE和ITAE)优化、稳定性裕量(Matlab代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...
Linux内核中断和Linux内核定时器
目录 Linux内核中断 Linux内核定时器 Linux内核中断 int request_irq(unsigned int irq, irq_handler_t handler, unsigned long flags,const char *name, void *dev) 功能:注册中断 参数: irq : 软中断号 gpio的软中断号 软中断号 gpio_to_i…...

OMG--IDL(Interface Definition Language)
OMG--IDL(Interface Definition Language) 1 概述2 内容缩写IDL 语法和语义概述词法约定ISO Latin-1的字母字符如下表十进制数字字符图形字符格式化字符Tokens注释标识符冲突规则转义标识符关键字IDL识别的其他字符字面量 预处理IDL 语法构建块核心数据类…...

英语学习:M开头
machine 机器 mad 发疯的,生气的 madam 女士,夫人 madame 夫人 magazine 杂志 magic 有魔力的 maid 女仆,侍女 mail 邮递 mailbox 邮箱 mainland 大陆 major 较大的,主要的 majority 大多数 male 雄的 man 人类 man…...
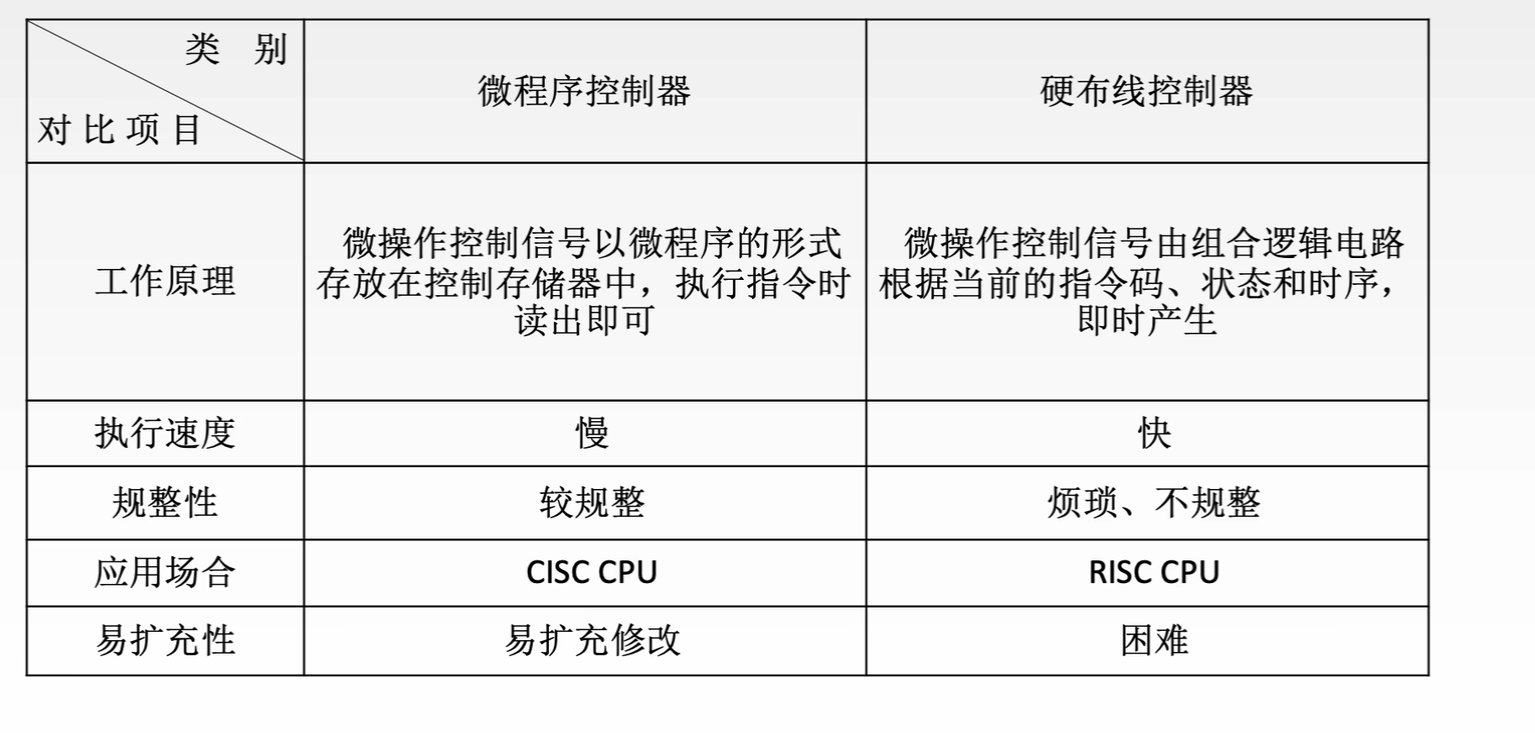
【计算机组成原理与体系结构】控制器
目录 一、CPU的功能与基本结构 二、指令周期的数据流 三、数据通路 四、硬布线控制器 五、微程序控制器 六、微指令 一、CPU的功能与基本结构 运算器基本结构 控制器基本结构 CPU的基本结构 二、指令周期的数据流 取址周期 间址周期 中断周期 指令周期流程 三、数据通路 …...

结构化命令
章节目录: 一、使用 if-then 语句二、if-then-else 语句三、嵌套 if 语句四、test 命令4.1 数值比较4.2 字符串比较4.3 文件比较 五、复合条件测试六、if-then 的高级特性6.1 使用单括号6.2 使用双括号6.3 使用双方括号 七、case 命令八、结束语 本章内容࿱…...
Java Web实训项目:西蒙购物网
文章目录 一、创建数据库和表1、创建数据库2、创建用户表3、创建类别表4、创建商品表5、创建订单表 二、创建Simonshop项目1、创建web项目2、修改Artifacts名称:simonshop3、重新部署项目4、编辑首页5、启动应用,查看效果 三、创建实体类1、用户实体类2、…...

ChatGPT Prompt 提示词设计技巧必知必会
本文内容整理自图灵社区直播《朱立成:ChatGPT Prompt提示词技巧必知必会》。 朱立成,图灵社区《ChatGPT即学即用》视频课程作者,软件工程师,对新事物充满好奇,关注ChatGPT应用。2001年毕业于浙江大学,从事软…...
尚硅谷-云尚办公-项目复盘
尚硅谷-云尚办公-项目复盘 资料地址本文介绍问题汇总问题1.knife4j无法下载 视频4问题2.dev等含义 视频5问题3.wrapper继承/实现图 视频8问题4.修改统一返回结果 视频11问题5.修改后新增也变修改 视频29问题6.redis中key值乱码 视频55-60问题7.RangeError: Maximum call stack …...
nacos升级到2.0.3(单机模式)
前提:https://github.com/alibaba/spring-cloud-alibaba/wiki/版本说明 Spring Cloud AlibabaSpring CloudSpring BootNacos2.2.7.RELEASESpring Cloud Hoxton.SR122.3.12.RELEASE2.0.3 一、pom.xml文件 <parent><groupId>org.springframework.boot&…...
Koa学习3:用户添加、错误处理
模型 在src目录下创建model目录,用来存放模型 创建用户模型 user.model.js 注意: UUID类型是无法自增的,将id设置为UUID类型时只需要为其指定默认值即可 // 数据类型 const { DataTypes } require(sequelize); // 导入已经连接了数据库…...
网络安全入门学习第十五课——PHP基础
文章目录 一、WEB技术1、什么是web2、B/S架构3、C/S架构 二、PHP概述1、PHP是什么2、PHP受欢迎的原因3、基于MVC模式的PHP框架4、常用编译工具5、PHP环境搭建6、开发工具 三、PHP基本语法格式1、标记2、输出语句3、注释4、标识符 四、数据与运算1、常量1.1、常量定义1.2、预定义…...
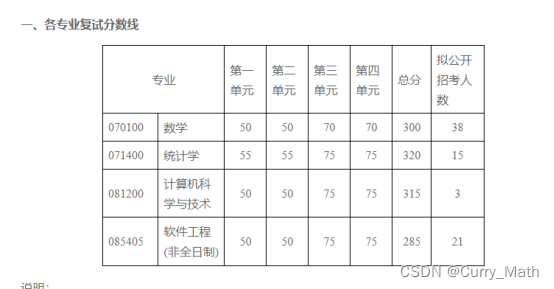
电子科技大学 数学专业-功不唐捐,玉汝于成
电子科技大学 数学专业 功不唐捐,玉汝于成 1.本科背景 本科是坐落于湖南湘潭的湖南科技大学,专业为网络工程专业,因热爱数学专业,所以决定跨考数学专业。 本科专业课平均成绩85,排名10/104。CET 4 474分,…...

Android10.0 iptables用IOemNetd实现删除子链功能的实现
1.前言 在10.0的系统rom定制化开发中,在system中netd网络这块的产品需要中,会要求设置屏蔽ip地址之内的功能, liunx中iptables命令也是比较重要的,接下来就来在IOemNetd这块实现删除创建子链的相关功能 2. iptables用IOemNetd实现删除创建子链功能的实现的核心类 syste…...

OpenGL光照之光照贴图
文章目录 漫反射贴图镜面光贴图放射光贴图代码 每个物体都拥有自己独特的材质从而对光照做出不同的反应的方法。这样子能够很容易在一个光照的场景中给每个物体一个独特的外观,但是这仍不能对一个物体的视觉输出提供足够多的灵活性。 我们将整个物体的材质定义为一个…...

2018~2019 学年第二学期《信息安全》考试试题(B 卷)
北京信息科技大学 2018 ~2019 学年第 2 学期 《信息安全》课程期末考试试卷 B 课程所在学院:计算机学院 适用专业班级:计科 1601-06,重修 考试形式:(闭卷) 一. 选择题(本题满分 10 分,共含 10 道小题,每小题 1 分) 网络中存在的安全漏洞主…...

日语AI面试高效通关秘籍:专业解读与青柚面试智能助攻
在如今就业市场竞争日益激烈的背景下,越来越多的求职者将目光投向了日本及中日双语岗位。但是,一场日语面试往往让许多人感到步履维艰。你是否也曾因为面试官抛出的“刁钻问题”而心生畏惧?面对生疏的日语交流环境,即便提前恶补了…...

oracle与MySQL数据库之间数据同步的技术要点
Oracle与MySQL数据库之间的数据同步是一个涉及多个技术要点的复杂任务。由于Oracle和MySQL的架构差异,它们的数据同步要求既要保持数据的准确性和一致性,又要处理好性能问题。以下是一些主要的技术要点: 数据结构差异 数据类型差异ÿ…...

2021-03-15 iview一些问题
1.iview 在使用tree组件时,发现没有set类的方法,只有get,那么要改变tree值,只能遍历treeData,递归修改treeData的checked,发现无法更改,原因在于check模式下,子元素的勾选状态跟父节…...

现代密码学 | 椭圆曲线密码学—附py代码
Elliptic Curve Cryptography 椭圆曲线密码学(ECC)是一种基于有限域上椭圆曲线数学特性的公钥加密技术。其核心原理涉及椭圆曲线的代数性质、离散对数问题以及有限域上的运算。 椭圆曲线密码学是多种数字签名算法的基础,例如椭圆曲线数字签…...

Module Federation 和 Native Federation 的比较
前言 Module Federation 是 Webpack 5 引入的微前端架构方案,允许不同独立构建的应用在运行时动态共享模块。 Native Federation 是 Angular 官方基于 Module Federation 理念实现的专为 Angular 优化的微前端方案。 概念解析 Module Federation (模块联邦) Modul…...
)
【服务器压力测试】本地PC电脑作为服务器运行时出现卡顿和资源紧张(Windows/Linux)
要让本地PC电脑作为服务器运行时出现卡顿和资源紧张的情况,可以通过以下几种方式模拟或触发: 1. 增加CPU负载 运行大量计算密集型任务,例如: 使用多线程循环执行复杂计算(如数学运算、加密解密等)。运行图…...

零基础设计模式——行为型模式 - 责任链模式
第四部分:行为型模式 - 责任链模式 (Chain of Responsibility Pattern) 欢迎来到行为型模式的学习!行为型模式关注对象之间的职责分配、算法封装和对象间的交互。我们将学习的第一个行为型模式是责任链模式。 核心思想:使多个对象都有机会处…...

06 Deep learning神经网络编程基础 激活函数 --吴恩达
深度学习激活函数详解 一、核心作用 引入非线性:使神经网络可学习复杂模式控制输出范围:如Sigmoid将输出限制在(0,1)梯度传递:影响反向传播的稳定性二、常见类型及数学表达 Sigmoid σ ( x ) = 1 1 +...

网络编程(UDP编程)
思维导图 UDP基础编程(单播) 1.流程图 服务器:短信的接收方 创建套接字 (socket)-----------------------------------------》有手机指定网络信息-----------------------------------------------》有号码绑定套接字 (bind)--------------…...

OPENCV形态学基础之二腐蚀
一.腐蚀的原理 (图1) 数学表达式:dst(x,y) erode(src(x,y)) min(x,y)src(xx,yy) 腐蚀也是图像形态学的基本功能之一,腐蚀跟膨胀属于反向操作,膨胀是把图像图像变大,而腐蚀就是把图像变小。腐蚀后的图像变小变暗淡。 腐蚀…...
