【深蓝学院】手写VIO第3章--基于优化的 IMU 与视觉信息融合--作业
0. 题目

1. T1
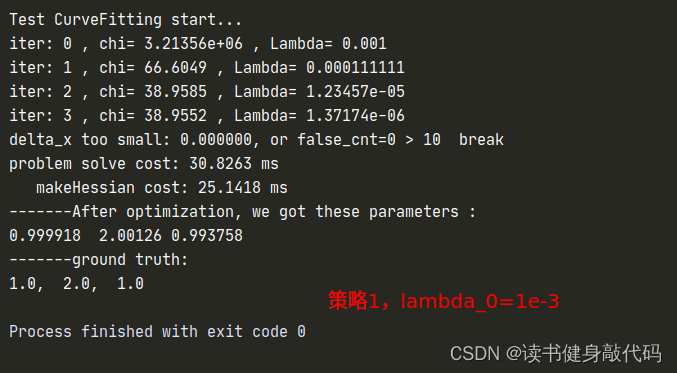
T1.1 绘制阻尼因子曲线
将尝试次数和lambda保存为csv,绘制成曲线如下图
iter, lambda
1, 0.002000
2, 0.008000
3, 0.064000
4, 1.024000
5, 32.768000
6, 2097.152000
7, 699.050667
8, 1398.101333
9, 5592.405333
10, 1864.135111
11, 1242.756741
12, 414.252247
13, 138.084082
14, 46.028027
15, 15.342676
16, 5.114225
17, 1.704742
18, 0.568247
19, 0.378832
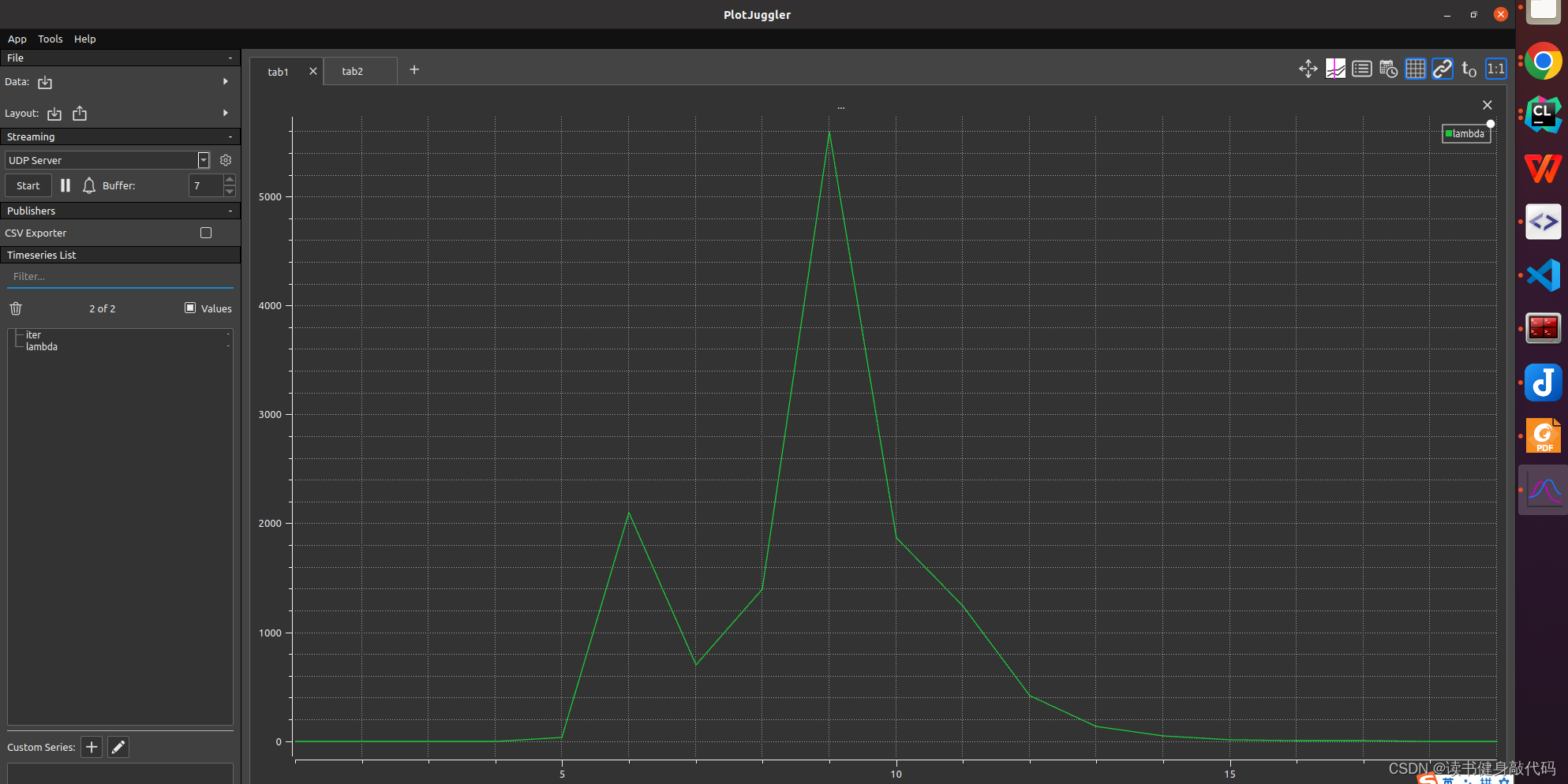
发现起始时刻的 μ \mu μ较小,步长 Δ x \Delta x Δx较大,导致cost上升,并未收敛,根据Nielsen策略,迅速调大 μ \mu μ,在求解 H Δ X = b H \Delta X=b HΔX=b时减小步长,不断迭代,在迭代过程中逐渐减小 μ \mu μ以增大步长加快收敛速度,满足优化终止条件之后停止优化(本题停止条件之一是误差下降超过1e6倍则停止优化)。
T1.2 更改目标函数
3处修改:
- 修改函数:
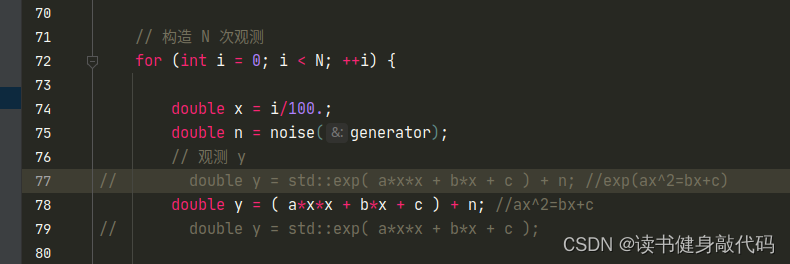
- 修改residual

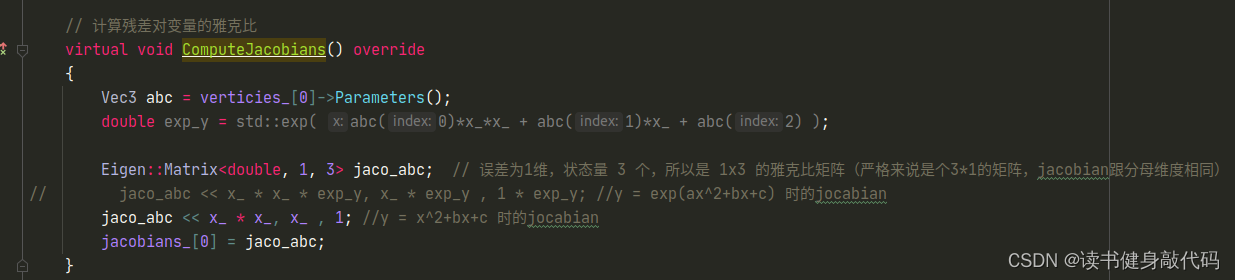
- 修改Jocabian
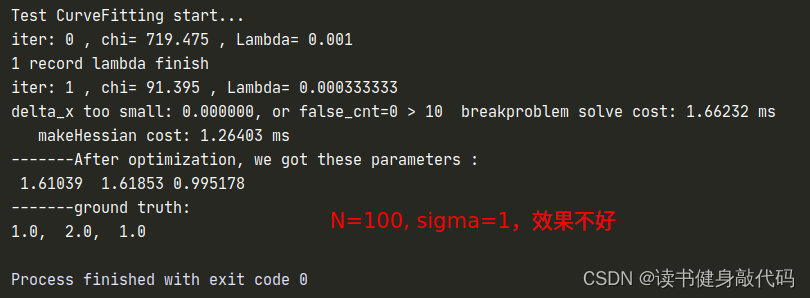
但是修改完之后发现拟合效果并不好,原观测数据服从 N ( 0 , 1 ) N(0,1) N(0,1)的正态分布,但是从 e x p ( a x 2 + b x + c ) exp(ax^2+bx+c) exp(ax2+bx+c)修改为 a x 2 + b x + c ax^2+bx+c ax2+bx+c之后, σ = 1 \sigma=1 σ=1显得有些大了(这个应该能从exp和二次函数的曲线分析出来,x正半轴二次函数比exp上升更快,真值相对于噪声观测值的误差也变得越大),所以要想获得更好的曲线拟合效果:1. 增加数据量;2. 减小噪声的variance以下是一些对比:
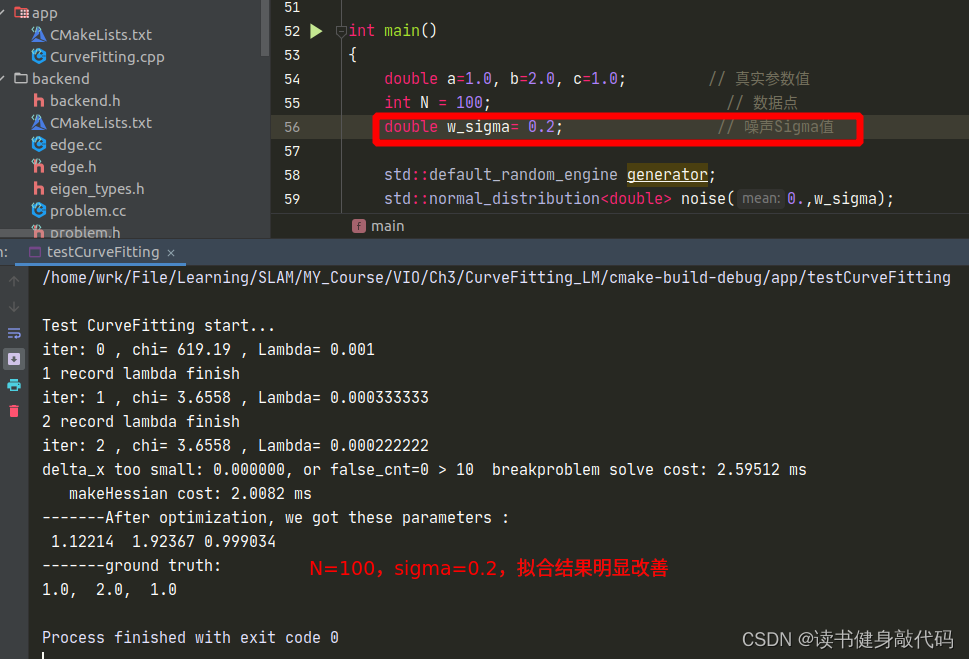
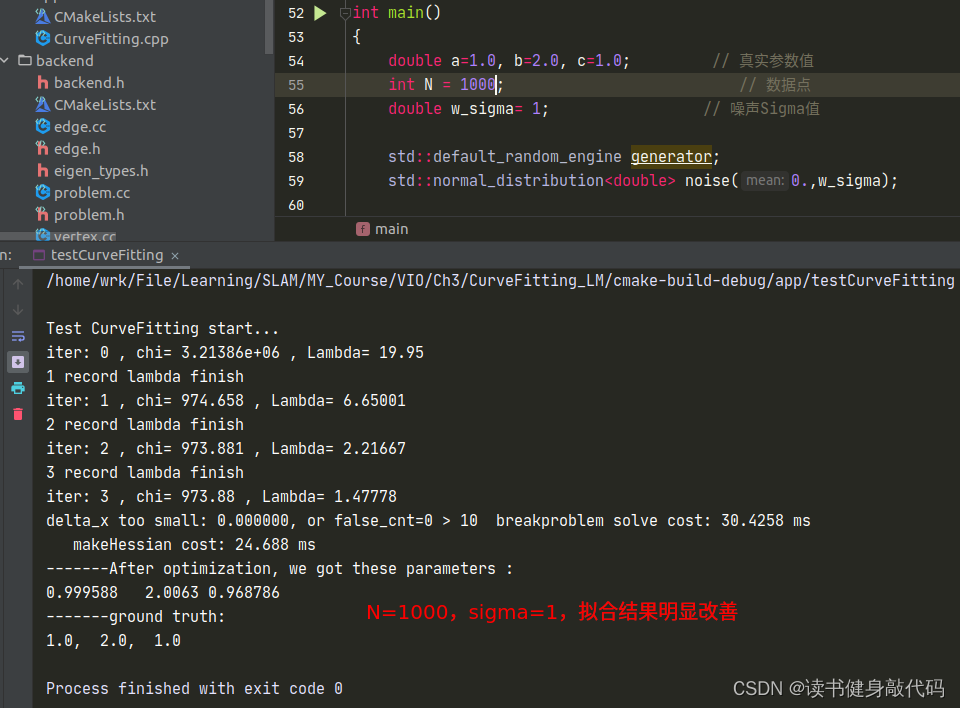
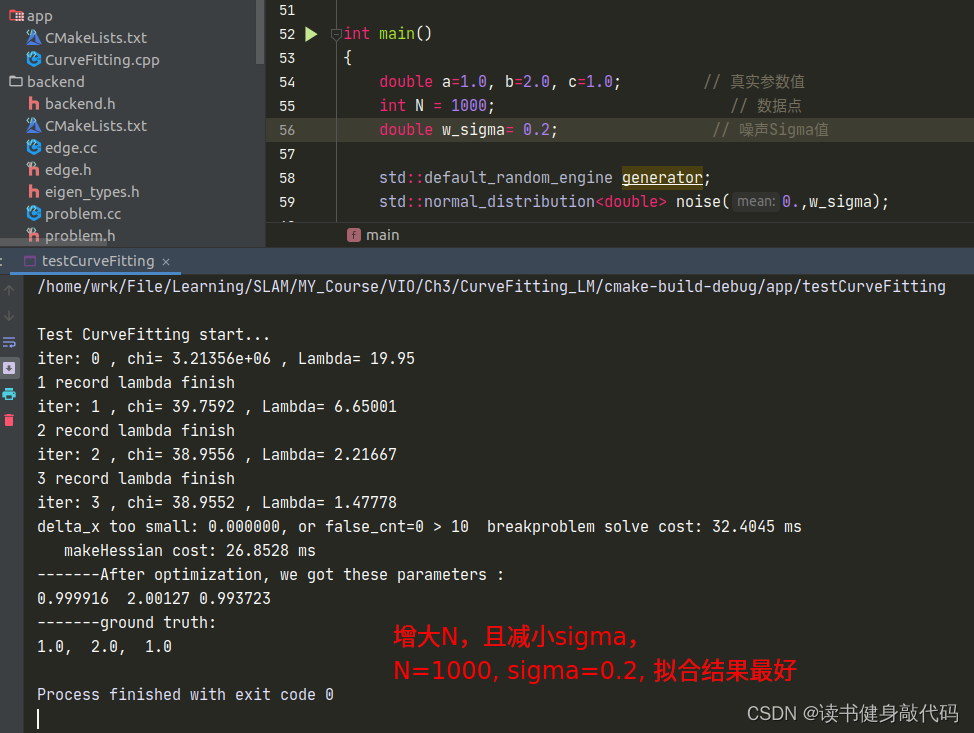
T1.3 不同的LM阻尼因子μ设置策略
参考论文 Henri Gavin. “The Levenberg-Marquardt method for nonlinear least squares curve-fitting problems”. In:Department of Civil and Environmental Engineering, Duke University (2011), pp. 1–15. 的4.1.1节:

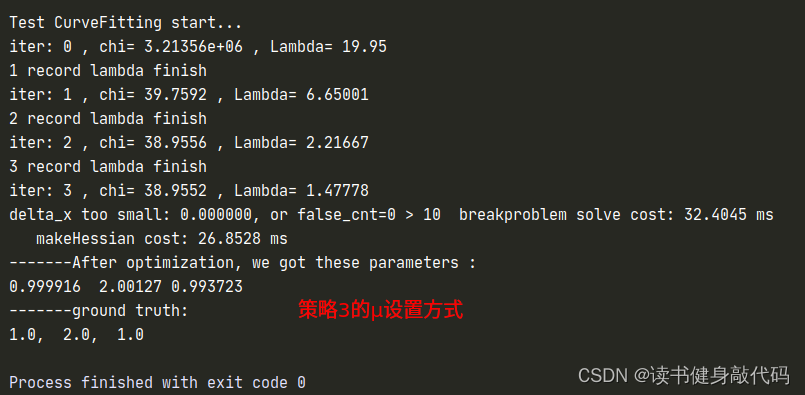
使用T1.2中的N=1000, σ = 0.2 \sigma=0.2 σ=0.2的参数进行实验。
1.3.1 策略3
第三种方法显然是Nelsion的设置方法,
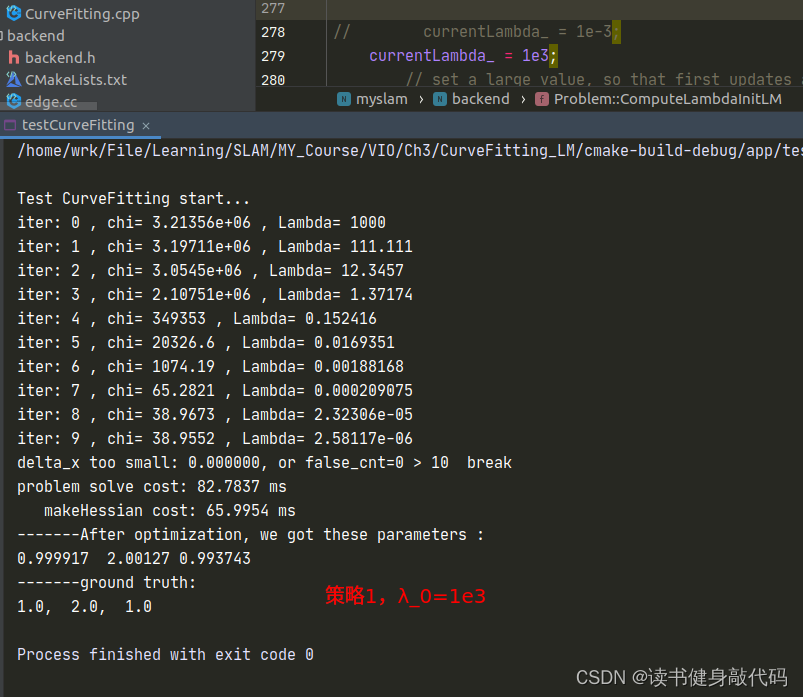
1.3.2 策略1
函数ComputeLambdaInitLM()
currentLambda_ = 1e-3; //选择不同的初值来实验
// currentLambda_ = 1e3;// set a large value, so that first updates are small steps in the steepest-descent direction
增减 λ \lambda λ:
void Problem::AddLambdatoHessianLM() {ulong size = Hessian_.cols();assert(Hessian_.rows() == Hessian_.cols() && "Hessian is not square");for (ulong i = 0; i < size; ++i) {
// Hessian_(i, i) += currentLambda_;Hessian_(i, i) += currentLambda_ * Hessian_(i, i); //理解: H(k+1) = H(k) + λ H(k) = (1+λ) H(k)}
}void Problem::RemoveLambdaHessianLM() {ulong size = Hessian_.cols();assert(Hessian_.rows() == Hessian_.cols() && "Hessian is not square");// TODO:: 这里不应该减去一个,数值的反复加减容易造成数值精度出问题?而应该保存叠加lambda前的值,在这里直接赋值for (ulong i = 0; i < size; ++i) {
// Hessian_(i, i) -= currentLambda_;Hessian_(i, i) /= 1.0 + currentLambda_;//H回退: H(k) = 1/(1+λ) * H(k+1)}
}
判断 λ \lambda λ是否好:
bool Problem::IsGoodStepInLM() {// 统计所有的残差double tempChi = 0.0;for (auto edge: edges_) {edge.second->ComputeResidual();tempChi += edge.second->Chi2();//计算cost}assert(Hessian_.rows() == Hessian_.cols() && "Hessian is not square");ulong size = Hessian_.cols();MatXX diag_hessian(MatXX::Zero(size, size));for(ulong i = 0; i < size; ++i) {diag_hessian(i, i) = Hessian_(i, i);}double scale = delta_x_.transpose() * (currentLambda_ * diag_hessian * delta_x_ + b_);//scale就是rho的分母double rho = (currentChi_ - tempChi) / scale;//计算rho// update currentLambda_double epsilon = 0.75;double L_down = 9.0;double L_up = 11.0;if(rho > epsilon && isfinite(tempChi)) {currentLambda_ = std::max(currentLambda_ / L_down, 1e-7);currentChi_ = tempChi;return true;} else {currentLambda_ = std::min(currentLambda_ * L_up, 1e7);return false;}
}
以上对比实验参考:https://note.youdao.com/ynoteshare/index.html?id=15a9ff86fedeb41d92f182e5cb3bace7&type=notebook&_time=1686390423162#/WEBbbb1c7ce04945f67a58c304455a56eda
但是得到了相反的结果,所以其结论我认为并不完全可信。而且原文中的时间相差并不大,不能说明什么问题,这只能说明lambda初值的设置对于收敛速度是有影响的。
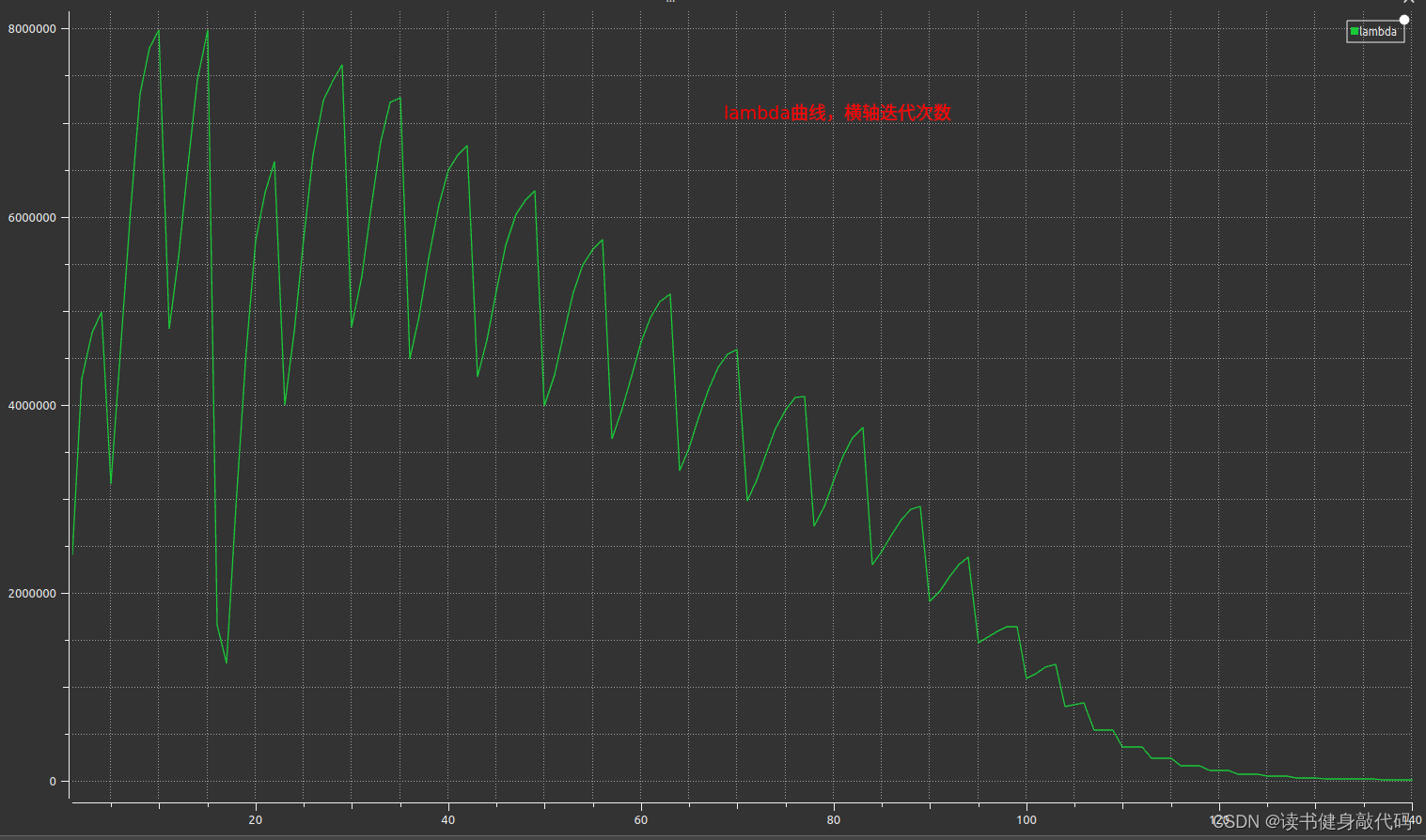
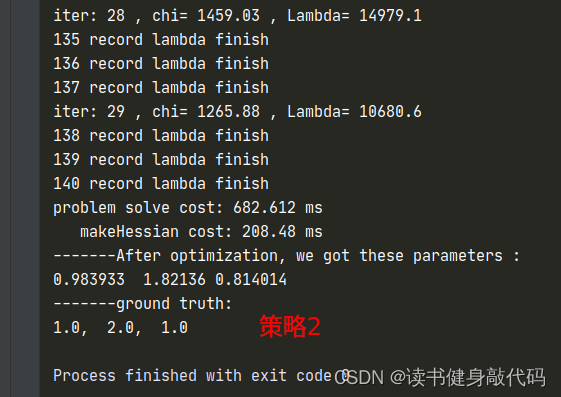
1.3.2 策略2
λ , Δ x , ρ \lambda, \Delta x,\rho λ,Δx,ρ计算同初值设置同策略3
只是计算cost时需要考虑 Δ x \Delta x Δx的系数,需要重新计算临时的cost,在满足更新x的条件之后在更新 α \alpha α和 x x x,自己实现了一版,但是这个运行时间让我感觉是有些问题的,放上代码和 λ \lambda λ的曲线,如果有大佬实现出来了告诉我一下~:
整个problem.cc文件
#include <iostream>
#include <fstream>
#include <eigen3/Eigen/Dense>
#include <glog/logging.h>
#include "backend/problem.h"
#include "utils/tic_toc.h"#ifdef USE_OPENMP#include <omp.h>#endifusing namespace std;//problem edge等构造函数后面第6讲会再讲,现在只先熟悉即可。namespace myslam {
namespace backend {
void Problem::LogoutVectorSize() {// LOG(INFO) <<// "1 problem::LogoutVectorSize verticies_:" << verticies_.size() <<// " edges:" << edges_.size();
}Problem::Problem(ProblemType problemType) :problemType_(problemType) {LogoutVectorSize();verticies_marg_.clear();
}Problem::~Problem() {}bool Problem::AddVertex(std::shared_ptr<Vertex> vertex) {if (verticies_.find(vertex->Id()) != verticies_.end()) {// LOG(WARNING) << "Vertex " << vertex->Id() << " has been added before";return false;} else {verticies_.insert(pair<unsigned long, shared_ptr<Vertex>>(vertex->Id(), vertex));}return true;
}bool Problem::AddEdge(shared_ptr<Edge> edge) {if (edges_.find(edge->Id()) == edges_.end()) {edges_.insert(pair<ulong, std::shared_ptr<Edge>>(edge->Id(), edge));} else {// LOG(WARNING) << "Edge " << edge->Id() << " has been added before!";return false;}for (auto &vertex: edge->Verticies()) {vertexToEdge_.insert(pair<ulong, shared_ptr<Edge>>(vertex->Id(), edge));//由vertex id查询edge}return true;
}bool Problem::Solve(int iterations) {if (edges_.size() == 0 || verticies_.size() == 0) {std::cerr << "\nCannot solve problem without edges or verticies" << std::endl;return false;}TicToc t_solve;// 统计优化变量的维数,为构建 H 矩阵做准备SetOrdering();// 遍历edge, 构建 H = J^T * J 矩阵MakeHessian();// LM 初始化ComputeLambdaInitLM();// LM 算法迭代求解bool stop = false;int iter = 0;//尝试的lambda次数try_iter_ = 0;//保存LM阻尼阻尼系数lambdafile_name_ = "./lambda.csv";FILE *tmp_fp = fopen(file_name_.data(), "w");fprintf(tmp_fp, "iter, lambda\n");fflush(tmp_fp);fclose(tmp_fp);while (!stop && (iter < iterations)) {std::cout << "iter: " << iter << " , chi= " << currentChi_ << " , Lambda= " << currentLambda_<< std::endl;bool oneStepSuccess = false;int false_cnt = 0;while (!oneStepSuccess) // 不断尝试 Lambda, 直到成功迭代一步{++try_iter_;// setLambdaAddLambdatoHessianLM();// 第四步,解线性方程 H X = BSolveLinearSystem();//RemoveLambdaHessianLM();// 优化退出条件1: delta_x_ 很小则退出if (delta_x_.squaredNorm() <= 1e-6 || false_cnt > 10) {stop = true;printf("delta_x too small: %f, or false_cnt=%d > 10 break\n", delta_x_.squaredNorm(), false_cnt);break;}// 更新状态量 X = X+ delta_xUpdateStates();// 判断当前步是否可行以及 LM 的 lambda 怎么更新oneStepSuccess = IsGoodStepInLM();//误差是否下降// 后续处理,if (oneStepSuccess) {// 在新线性化点 构建 hessianalpha_ = alpha_tmp_;MakeHessian();// TODO:: 这个判断条件可以丢掉,条件 b_max <= 1e-12 很难达到,这里的阈值条件不应该用绝对值,而是相对值
// double b_max = 0.0;
// for (int i = 0; i < b_.size(); ++i) {
// b_max = max(fabs(b_(i)), b_max);
// }
// // 优化退出条件2: 如果残差 b_max 已经很小了,那就退出
// stop = (b_max <= 1e-12);false_cnt = 0;} else {false_cnt++;RollbackStates(); // 误差没下降,回滚}}iter++;// 优化退出条件3: currentChi_ 跟第一次的chi2相比,下降了 1e6 倍则退出if (sqrt(currentChi_) <= stopThresholdLM_) {printf("currentChi_ decrease matched break condition");stop = true;}}std::cout << "problem solve cost: " << t_solve.toc() << " ms" << std::endl;std::cout << " makeHessian cost: " << t_hessian_cost_ << " ms" << std::endl;return true;
}void Problem::SetOrdering() {// 每次重新计数ordering_poses_ = 0;ordering_generic_ = 0;ordering_landmarks_ = 0;// Note:: verticies_ 是 map 类型的, 顺序是按照 id 号排序的// 统计带估计的所有变量的总维度for (auto vertex: verticies_) {ordering_generic_ += vertex.second->LocalDimension(); // 所有的优化变量总维数}
}//可以暂时不看,后面会再讲
void Problem::MakeHessian() {TicToc t_h;// 直接构造大的 H 矩阵ulong size = ordering_generic_;MatXX H(MatXX::Zero(size, size));VecX b(VecX::Zero(size));// TODO:: accelate, accelate, accelate
//#ifdef USE_OPENMP
//#pragma omp parallel for
//#endif// 遍历每个残差,并计算他们的雅克比,得到最后的 H = J^T * Jfor (auto &edge: edges_) {edge.second->ComputeResidual();edge.second->ComputeJacobians();auto jacobians = edge.second->Jacobians();auto verticies = edge.second->Verticies();assert(jacobians.size() == verticies.size());for (size_t i = 0; i < verticies.size(); ++i) {auto v_i = verticies[i];if (v_i->IsFixed()) continue; // Hessian 里不需要添加它的信息,也就是它的雅克比为 0auto jacobian_i = jacobians[i];ulong index_i = v_i->OrderingId();ulong dim_i = v_i->LocalDimension();MatXX JtW = jacobian_i.transpose() * edge.second->Information();for (size_t j = i; j < verticies.size(); ++j) {auto v_j = verticies[j];if (v_j->IsFixed()) continue;auto jacobian_j = jacobians[j];ulong index_j = v_j->OrderingId();ulong dim_j = v_j->LocalDimension();assert(v_j->OrderingId() != -1);MatXX hessian = JtW * jacobian_j;// 所有的信息矩阵叠加起来H.block(index_i, index_j, dim_i, dim_j).noalias() += hessian;if (j != i) {// 对称的下三角H.block(index_j, index_i, dim_j, dim_i).noalias() += hessian.transpose();}}b.segment(index_i, dim_i).noalias() -= JtW * edge.second->Residual();}}Hessian_ = H;b_ = b;t_hessian_cost_ += t_h.toc();delta_x_ = VecX::Zero(size); // initial delta_x = 0_n;}/*
* Solve Hx = b, we can use PCG iterative method or use sparse Cholesky
*/
void Problem::SolveLinearSystem() {delta_x_ = Hessian_.inverse() * b_;
// delta_x_ = H.ldlt().solve(b_);}void Problem::UpdateStates() {for (auto vertex: verticies_) {ulong idx = vertex.second->OrderingId();ulong dim = vertex.second->LocalDimension();VecX delta = delta_x_.segment(idx, dim);// 所有的参数 x 叠加一个增量 x_{k+1} = x_{k} + delta_xvertex.second->Plus( alpha_ * delta);}
}void Problem::RollbackStates() {for (auto vertex: verticies_) {ulong idx = vertex.second->OrderingId();ulong dim = vertex.second->LocalDimension();VecX delta = delta_x_.segment(idx, dim);// 之前的增量加了后使得损失函数增加了,我们应该不要这次迭代结果,所以把之前加上的量减去。vertex.second->Plus(alpha_ * (-delta));}
}/// LM
void Problem::ComputeLambdaInitLM() {ni_ = 2.;
// currentLambda_ = -1.;currentChi_ = 0.0;// TODO:: robust cost chi2for (auto edge: edges_) {currentChi_ += edge.second->Chi2();}if (err_prior_.rows() > 0)currentChi_ += err_prior_.norm();stopThresholdLM_ = 1e-6 * currentChi_; // 迭代条件为 误差下降 1e-6 倍double maxDiagonal = 0;ulong size = Hessian_.cols();assert(Hessian_.rows() == Hessian_.cols() && "Hessian is not square");for (ulong i = 0; i < size; ++i) {maxDiagonal = std::max(fabs(Hessian_(i, i)), maxDiagonal);//取H矩阵的最大值,然后*涛}double tau = 1e-5;currentLambda_ = tau * maxDiagonal;// currentLambda_ = 1e-3;
// currentLambda_ = 1e3;// set a large value, so that first updates are small steps in the steepest-descent direction}//这个关于Hessian矩阵的我还搞不懂
void Problem::AddLambdatoHessianLM() {ulong size = Hessian_.cols();assert(Hessian_.rows() == Hessian_.cols() && "Hessian is not square");for (ulong i = 0; i < size; ++i) {Hessian_(i, i) += currentLambda_; //策略2,3
// Hessian_(i, i) += currentLambda_ * Hessian_(i, i); //理解: H(k+1) = H(k) + λ H(k) = (1+λ) H(k) 策略1}
}void Problem::RemoveLambdaHessianLM() {ulong size = Hessian_.cols();assert(Hessian_.rows() == Hessian_.cols() && "Hessian is not square");// TODO:: 这里不应该减去一个,数值的反复加减容易造成数值精度出问题?而应该保存叠加lambda前的值,在这里直接赋值for (ulong i = 0; i < size; ++i) {Hessian_(i, i) -= currentLambda_; //策略2,3
// Hessian_(i, i) /= 1.0 + currentLambda_;//H回退: H(k) = 1/(1+λ) * H(k+1),策略1}
}//Nielsen的方法,分母直接为L,判断\rho的符号
bool Problem::IsGoodStepInLM() {bool ret = false;/*策略2更新策略*/
// double scale = 0;
// scale = delta_x_.transpose() * (currentLambda_ * delta_x_ + b_);
// scale += 1e-3; // make sure it's non-zero :)// recompute residuals after update state// 统计所有的残差double tempChi_p_h = 0.0, tempChi_p_alpha_h = 0.0;for (auto edge: edges_) {edge.second->ComputeResidual();tempChi_p_h += edge.second->Chi2();//计算cost}double alpha_up = b_.transpose() * delta_x_;double alpha_down = (tempChi_p_h - currentChi_) / 2. + 2. * alpha_up;alpha_tmp_ = alpha_up / alpha_down;double scale = 0;scale = alpha_tmp_ * delta_x_.transpose() * (currentLambda_ * alpha_tmp_ * delta_x_ + b_);scale += 1e-3; // make sure it's non-zero :)HashEdge tmp_edges = edges_;HashVertex tmp_vertecies = verticies_;//更新x以计算新的costfor (auto vertex: tmp_vertecies) {ulong idx = vertex.second->OrderingId();ulong dim = vertex.second->LocalDimension();VecX delta = delta_x_.segment(idx, dim);// 所有的参数 x 叠加一个增量 x_{k+1} = x_{k} + delta_xvertex.second->Plus(alpha_tmp_ * delta);}for (auto edge: tmp_edges) {edge.second->ComputeResidual();tempChi_p_alpha_h += edge.second->Chi2();//计算cost}double rho_alpha_h = (tempChi_p_alpha_h - currentChi_) / scale; //tempChi的计算中的alpha*delta_x已经在x = x + alpha*delta_x更新的时候算上了if (rho_alpha_h > 0 && isfinite(tempChi_p_alpha_h)) { // last step was good, 误差在下降currentLambda_ = std::max(currentLambda_ / (1 + alpha_tmp_), 1e-7);currentChi_ = tempChi_p_h; //这里应该是用现在的,而不是临时更新出来的,在外面更新ret = true;} else {currentLambda_ = currentLambda_ + fabs(tempChi_p_alpha_h - currentChi_) / (2 * alpha_tmp_);ret = false;}/*策略2更新策略*/FILE *fp_lambda = fopen(file_name_.data(), "a");fprintf(fp_lambda, "%d, %f\n", try_iter_, currentLambda_);fflush(fp_lambda);fclose(fp_lambda);printf("%d record lambda finish\n", try_iter_);return ret;
}/** @brief conjugate gradient with perconditioning
*
* the jacobi PCG method
*
*/
VecX Problem::PCGSolver(const MatXX &A, const VecX &b, int maxIter = -1) {assert(A.rows() == A.cols() && "PCG solver ERROR: A is not a square matrix");int rows = b.rows();int n = maxIter < 0 ? rows : maxIter;VecX x(VecX::Zero(rows));MatXX M_inv = A.diagonal().asDiagonal().inverse();VecX r0(b); // initial r = b - A*0 = bVecX z0 = M_inv * r0;VecX p(z0);VecX w = A * p;double r0z0 = r0.dot(z0);double alpha = r0z0 / p.dot(w);VecX r1 = r0 - alpha * w;int i = 0;double threshold = 1e-6 * r0.norm();while (r1.norm() > threshold && i < n) {i++;VecX z1 = M_inv * r1;double r1z1 = r1.dot(z1);double belta = r1z1 / r0z0;z0 = z1;r0z0 = r1z1;r0 = r1;p = belta * p + z1;w = A * p;alpha = r1z1 / p.dot(w);x += alpha * p;r1 -= alpha * w;}return x;
}}
}
2. 推导公式
2.2 f 15 f_{15} f15
同样地, α b i b k + 1 \alpha_{b_ib_{k+1}} αbibk+1将a带入之后也只与下图的红色部分有关

于是剩下的为:(其实不明白为什么最后有的项还会有 ω \omega ω)
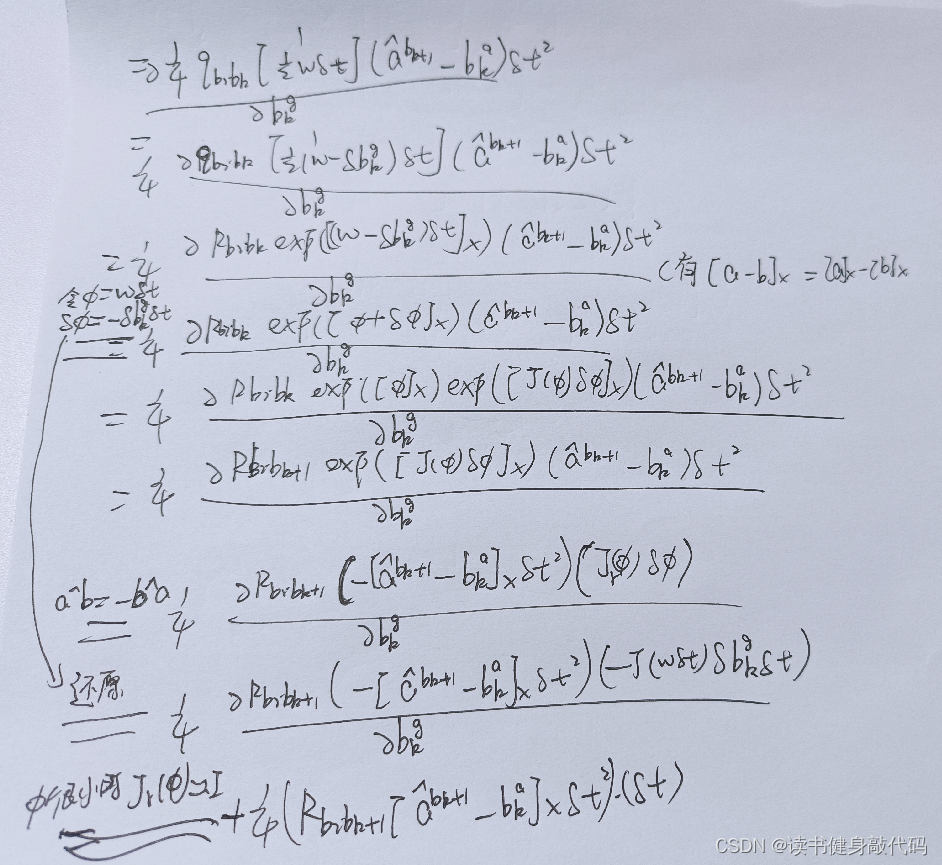
其中令 ϕ = ω δ t , δ ϕ = − δ b k g δ t \phi=\omega\delta t,\delta\phi=-\delta b_k^g\delta t ϕ=ωδt,δϕ=−δbkgδt很关键,并用了下述公式:

2.2 g 12 g_{12} g12

所以刚才的疑问,为什么有的会有 ω \omega ω,那是在那一项将 ω \omega ω展开之后也跟被导量无关的时候才会不展开 ω \omega ω,比如 f 22 f_{22} f22中, ω \omega ω的展开量对角度 θ \theta θ是无关的,所以可以保留 ω \omega ω。
2.3 推导总结
针对被导量,将分母展开,取与被导量有关的项进行求导,无关的都扔掉,比如大多数导数都对 n k g , n k a n_k^g,n_k^a nkg,nka无关,所以有时候干脆不写,直接扔掉了,但是像2.2节中的与n_k^g有关,所以就反而只与 n k g n_k^g nkg有关,把握这个原则就能推出其它。
3. T3
式(9)来源:
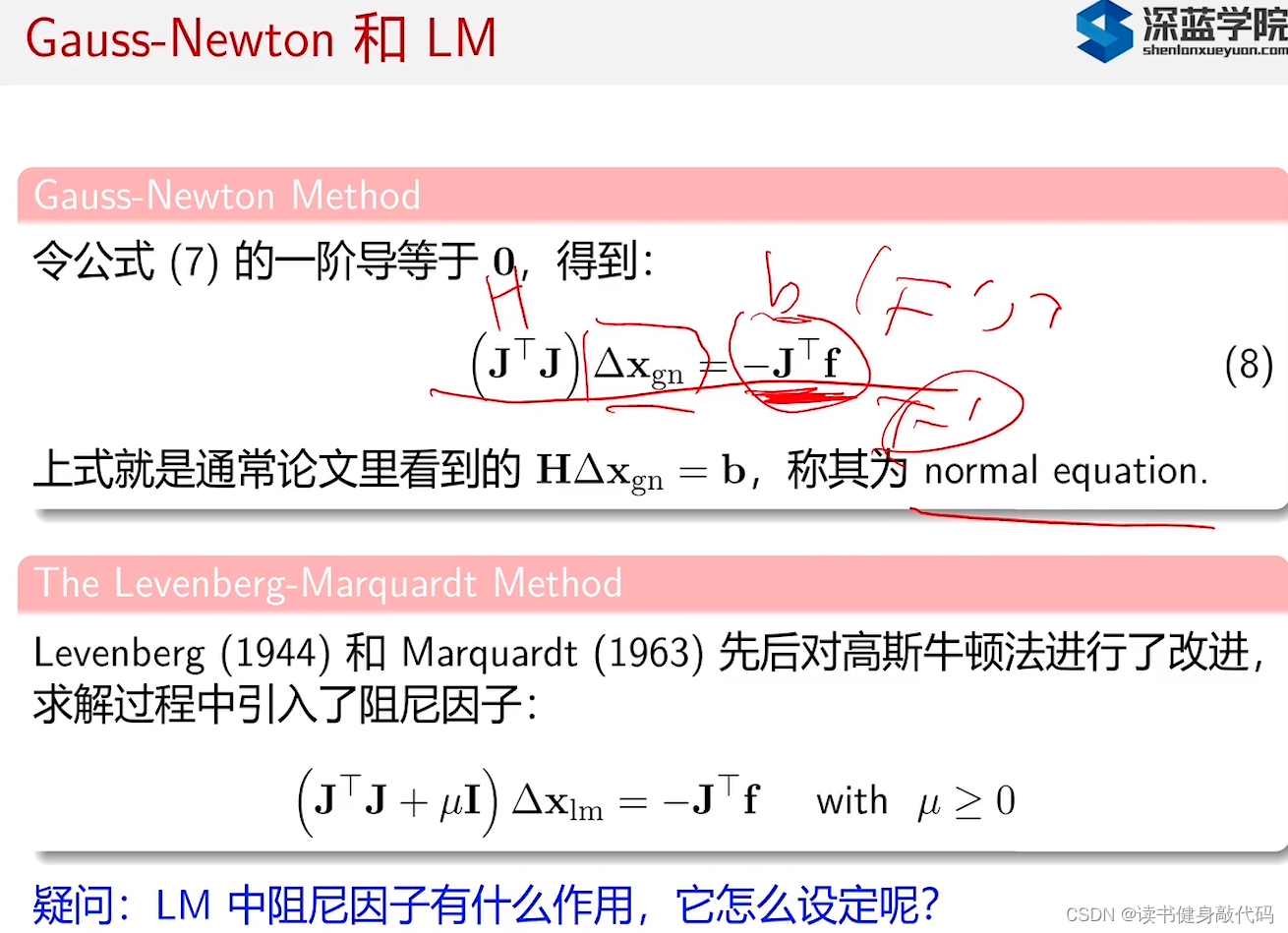

图片来自(不想去水印了):博客
数学基础太差,有些看不懂怎么把前面系数项移到右边的。

助教给的答案也看不太懂:
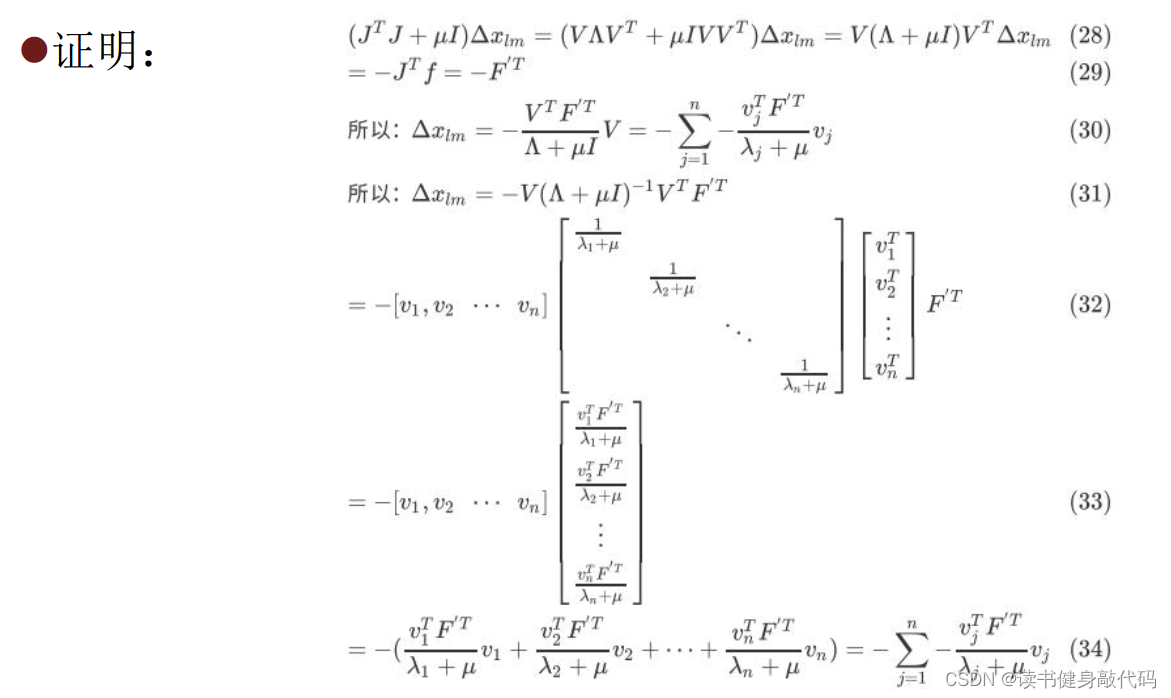
本章完。
相关文章:

【深蓝学院】手写VIO第3章--基于优化的 IMU 与视觉信息融合--作业
0. 题目 1. T1 T1.1 绘制阻尼因子曲线 将尝试次数和lambda保存为csv,绘制成曲线如下图 iter, lambda 1, 0.002000 2, 0.008000 3, 0.064000 4, 1.024000 5, 32.768000 6, 2097.152000 7, 699.050667 8, 1398.101333 9, 5592.405333 10, 1864.135111 11, 1242.7567…...

企业级信息系统开发讲课笔记4.11 Spring Boot中Spring MVC的整合支持
文章目录 零、学习目标一、Spring MVC 自动配置(一)自动配置概述(二)Spring Boot整合Spring MVC 的自动化配置功能特性 二、Spring MVC 功能拓展实现(一)创建Spring Boot项目 - SpringMvcDemo2021ÿ…...

chatgpt赋能python:Python安装EGG——一个简单的指南
Python安装EGG——一个简单的指南 如果你使用Python有一段时间了,你可能会遇到需要安装扩展包(Package)的情况。在Python中,这些扩展包的文件格式通常是.egg(Easy Installable GZip)。在本文中,…...

Web前端-React学习
React基础 React 概述 React 是一个用于构建用户界面的JavaScript库。 用户界面: HTML页面(前端) React主要用来写HTML页面, 或构建Web应用 如果从MVC的角度来看,React仅仅是视图层(V),也就…...

【Rust项目实战】sensleak,扫描 Git 仓库中的敏感信息
github仓库:https://github.com/open-rust-initiative/sensleak-rs Rust是一门神奇的编程语言,它提供了内存安全、零成本抽象、并发安全等特性,使开发人员能够编写高性能、高抽象和安全的代码。 这是我用rust开发的第一个工作,希望…...

搭建一个定制版New Bing吧
项目介绍 项目地址:https://github.com/adams549659584/go-proxy-bingai 引用项目简介:用 Vue3 和 Go 搭建的微软 New Bing 演示站点,拥有一致的 UI 体验,支持 ChatGPT 提示词,国内可用,国内可用ÿ…...

使用AIGC工具提升论文阅读效率
大家好,我是herosunly。985院校硕士毕业,现担任算法研究员一职,热衷于机器学习算法研究与应用。曾获得阿里云天池比赛第一名,CCF比赛第二名,科大讯飞比赛第三名。拥有多项发明专利。对机器学习和深度学习拥有自己独到的见解。曾经辅导过若干个非计算机专业的学生进入到算法…...

本周大新闻|Vision Pro头显重磅发布;苹果收购AR厂商Mira
本周XR大新闻,上周Quest 3发布之后,本周苹果MR头显Vision Pro正式发布,也是本周AR/VR新闻的重头戏。 AR方面,苹果发布VST头显Vision Pro(虽然本质是台VR,但以AR场景为核心)以及visionOS&…...

在Spring Boot微服务使用JedisCluster操作Redis集群String字符串
记录:449 场景:在Spring Boot微服务使用JedisCluster操作Redis集群的String字符串数据类型。 版本:JDK 1.8,Spring Boot 2.6.3,redis-6.2.5,jedis-3.7.1。 1.微服务中配置Redis信息 1.1在pom.xml添加依赖 pom.xml文件: <…...
5.1 合并数据
5.1 合并数据 5.1.1 堆叠合并数据1、横向堆叠 concat()2、纵向堆叠 concat()和append() 5.1.2 主键合并数据 merge()和join()5.1.3 重叠合并数据 combine_first() 5.1.1 堆叠合并数据 堆叠就是简单地把两个表拼在一起,也被称作轴向连接、绑定或连接。依照连接轴的方…...

华为OD机试真题 JavaScript 实现【求解立方根】【牛客练习题】
一、题目描述 计算一个浮点数的立方根,不使用库函数。保留一位小数。 数据范围:∣val∣≤20 。 二、输入描述 待求解参数,为double类型(一个实数) 三、输出描述 输出参数的立方根。保留一位小数。 四、解题思路…...
初探BERTPre-trainSelf-supervise
初探Bert 因为一次偶然的原因,自己有再次对Bert有了一个更深层地了解,特别是对预训练这个概念,首先说明,自己是看了李宏毅老师的讲解,这里只是尝试进行简单的总结复述并加一些自己的看法。 说Bert之前不得不说现在的…...

Ficus 第二弹,突破限制器的 Markdown 编辑管理软件!
大家好,我们是 ggG 团队,我们开发的 markdown 笔记管理软件 Ficus Beta 版本正式发布了。详情可以见我们官网,也可以来我们仓库查看。 相对于 Alpha 版本(可以在我们之前的博客中查看),主要有 3 点明显的提…...
基于Springboot+vue+协同过滤+前后端分离+鲜花商城推荐系统(用户,多商户,管理员)+全套视频教程
基于Springbootvue协同过滤前后端分离鲜花商城推荐系统(用户,多商户,管理员)(毕业论文11000字以上,共33页,程序代码,MySQL数据库) 代码下载: 链接:https://pan.baidu.com/s/1mf2rsB_g1DutFEXH0bPCdA 提取码:8888 【运行环境】Idea JDK1.8 Maven MySQL…...
MixQuery系列(一):多数据源混合查询引擎调研
背景 存储情况 当前的存储引擎可谓百花齐放,层出不穷。为什么会这样了?因为不存在One for all的存储,不同的存储总有不同的存储的优劣和适用场景。因此,在实际的业务场景中,不同特点的数据会存储到不同的存储引擎里。 业务挑战 然而异构的存储和数据源,却给分析查询带…...
d2l学习——第一章Introduction
x.0 环境配置 使用d2l库,安装如下: conda create --name d2l python3.9 -y conda activate d2lpip install torch1.12.0 torchvision0.13.0 pip install d2l1.0.0b0mkdir d2l-en && cd d2l-en curl https://d2l.ai/d2l-en.zip -o d2l-en.zip u…...
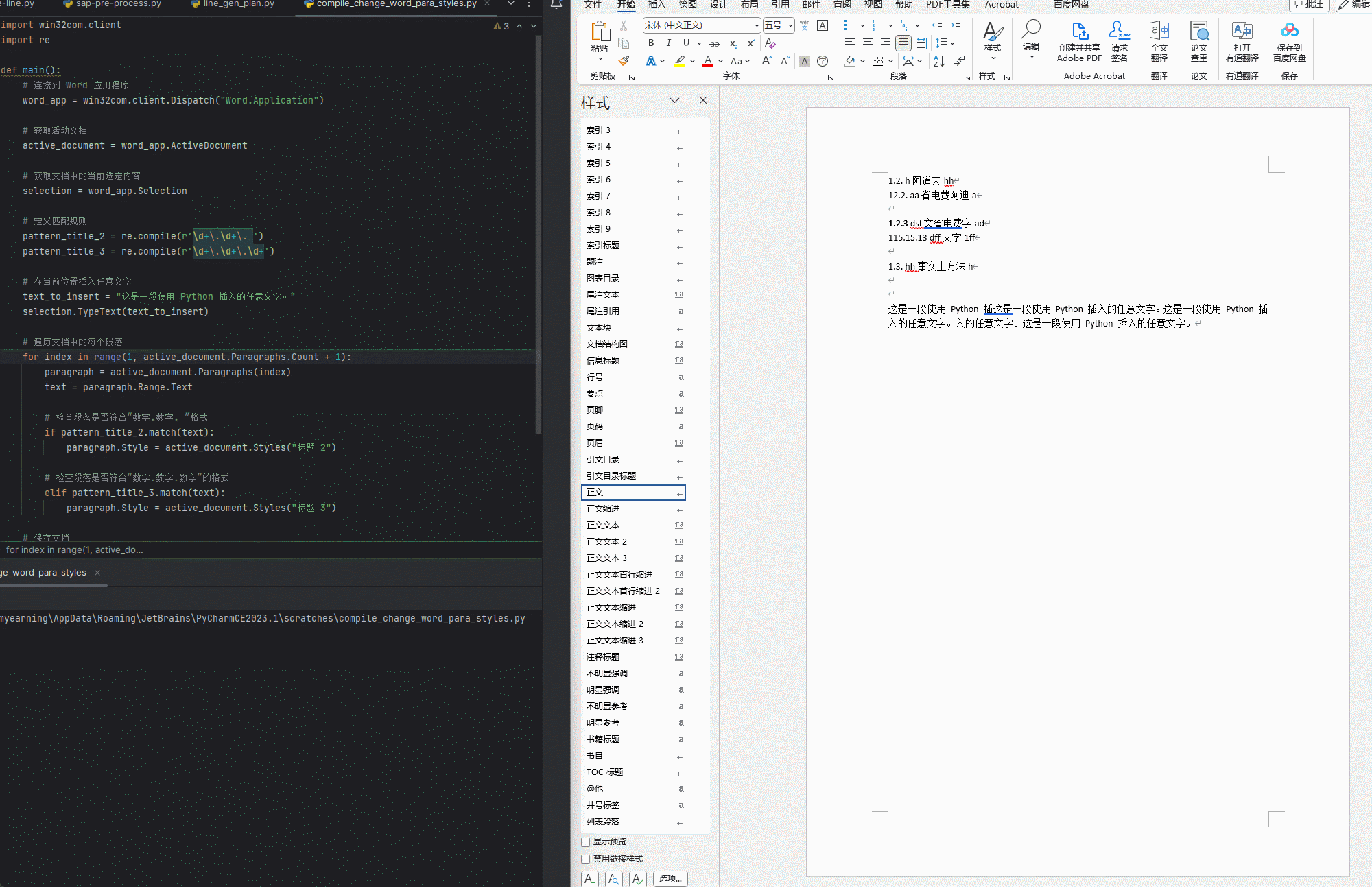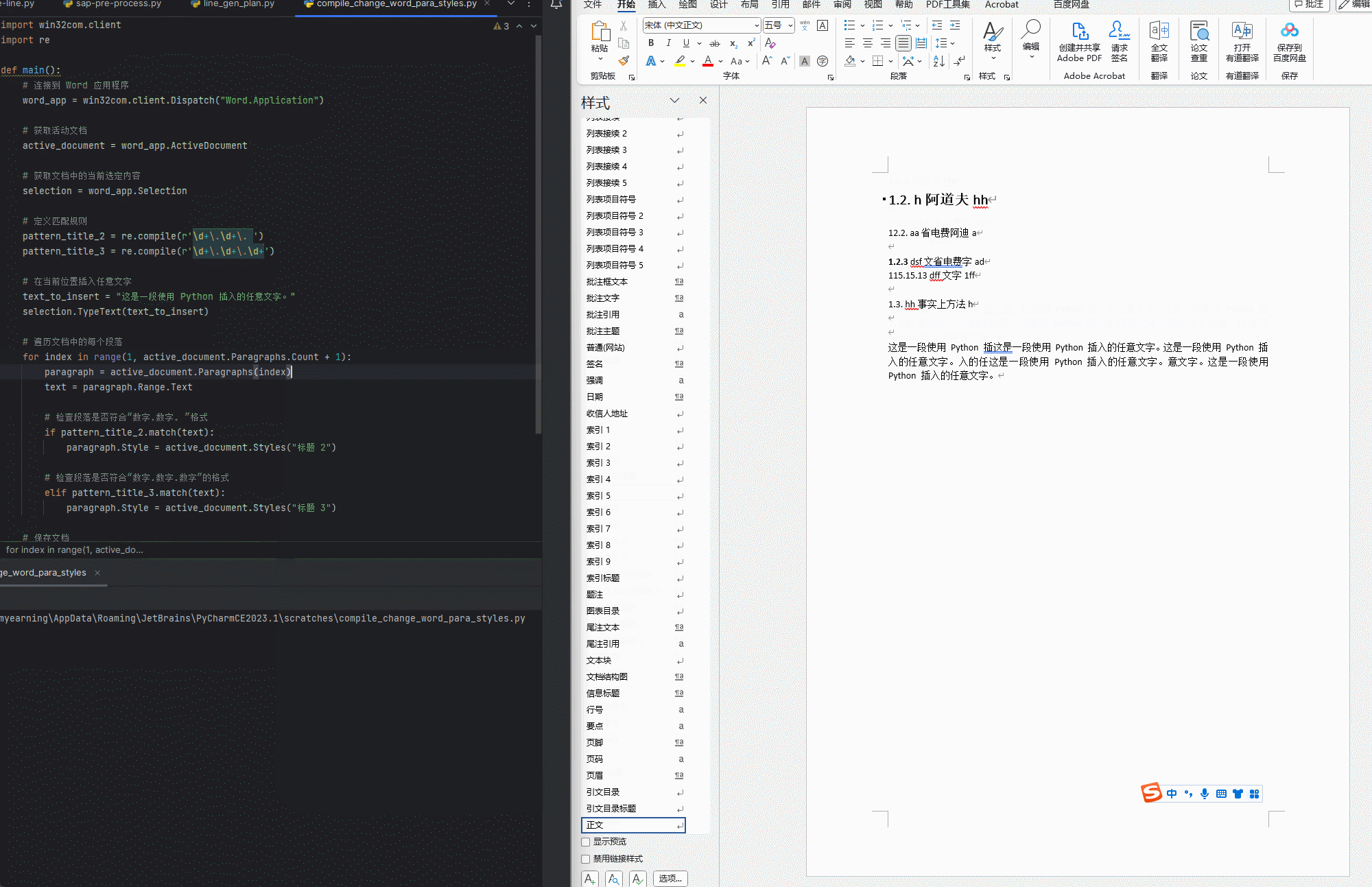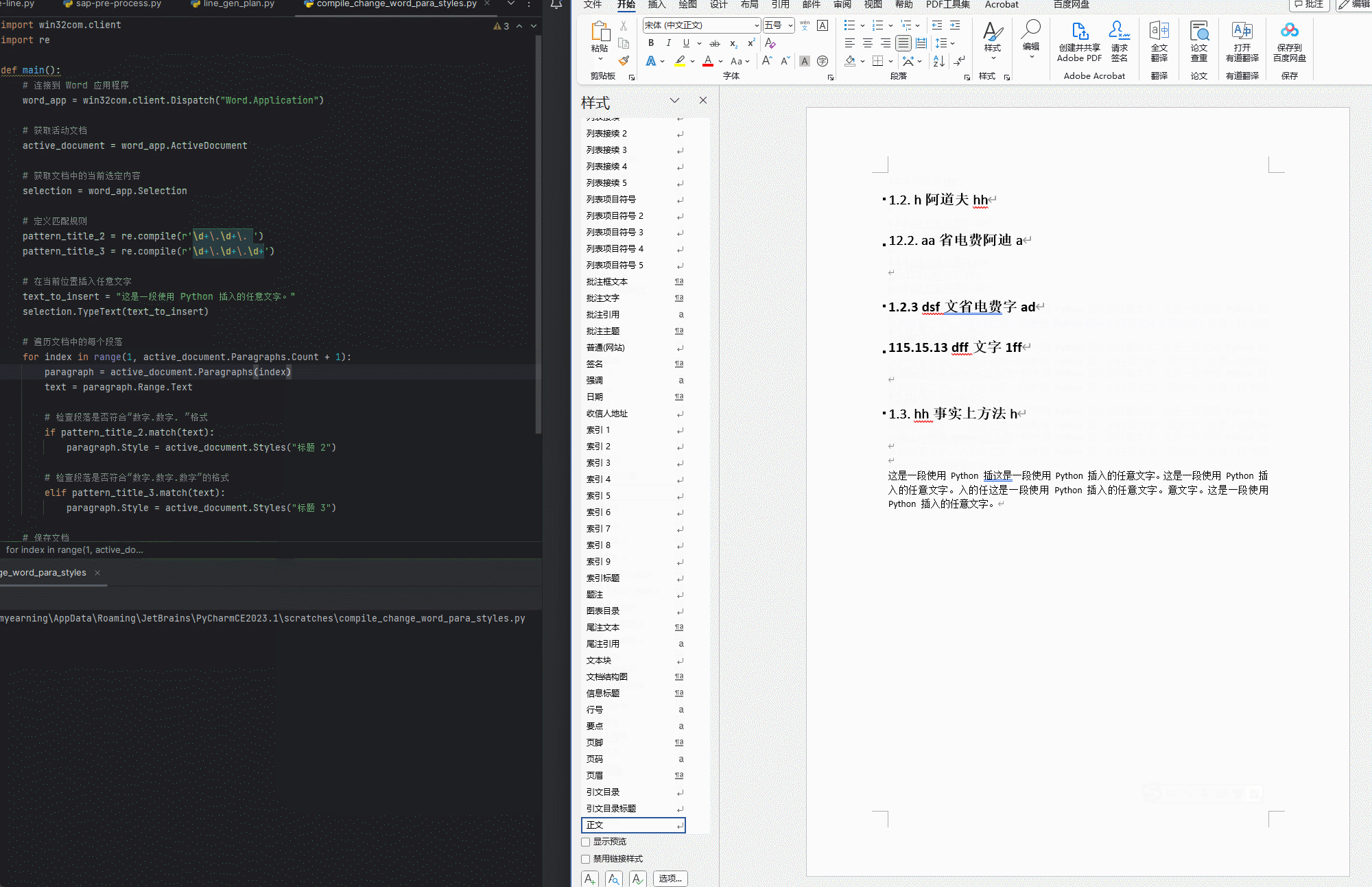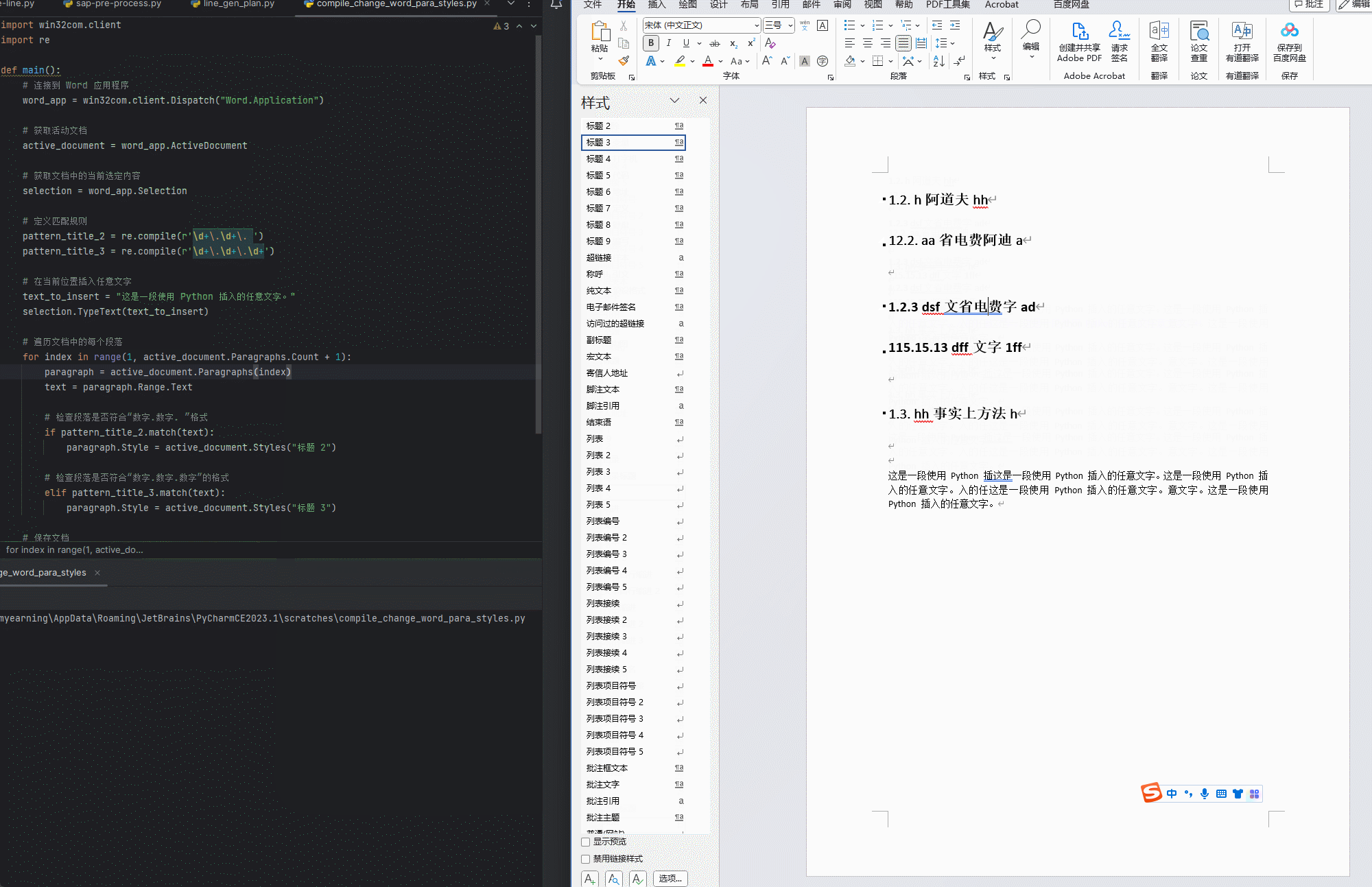
【python】【Word】用正则表达式匹配正文中的标题(未使用样式)并通过win32com指定相应样式
标题的格式 二级标题: 数字.数字. 文字 三级标题:数字.数字.数字 文字 python代码 使用方法 只保留一个需要应用的WORD文档运行程序,逐行匹配 使用效果 代码 import win32com.client import redef compile_change_Word_titlestyle():#…...
)
Matlab实现光伏仿真(附上完整仿真源码)
光伏发电电池模型是描述光伏电池在不同条件下产生电能的数学模型。该模型可以用于预测光伏电池的输出功率,并为优化光伏电池系统设计和控制提供基础。本文将介绍如何使用Matlab实现光伏发电电池模型。 文章目录 1、光伏发电电池模型2、使用Matlab实现光伏发电电池模…...

JVM零基础到高级实战之Java内存区域方法区
JVM零基础到高级实战之Java内存区域方法区 JVM零基础到高级实战之Java内存区域方法区 文章目录 JVM零基础到高级实战之Java内存区域方法区前言JVM内存模型之JAVA方法区总结 前言 JVM零基础到高级实战之Java内存区域方法区 JVM内存模型之JAVA方法区 JAVA方法区是什么…...

SpringCloud-stream一体化MQ解决方案-消费者组
参考资料: 参考demo 参考视频1 参考视频2 官方文档(推荐) 官方文档中文版 关于Kafka和rabbitMQ的安装教程,见本人之前的博客 rocketMq的安装教程 rocketMq仪表盘安装教程 重!!!...

RocketMQ延迟消息机制
两种延迟消息 RocketMQ中提供了两种延迟消息机制 指定固定的延迟级别 通过在Message中设定一个MessageDelayLevel参数,对应18个预设的延迟级别指定时间点的延迟级别 通过在Message中设定一个DeliverTimeMS指定一个Long类型表示的具体时间点。到了时间点后…...

【Java学习笔记】Arrays类
Arrays 类 1. 导入包:import java.util.Arrays 2. 常用方法一览表 方法描述Arrays.toString()返回数组的字符串形式Arrays.sort()排序(自然排序和定制排序)Arrays.binarySearch()通过二分搜索法进行查找(前提:数组是…...

在WSL2的Ubuntu镜像中安装Docker
Docker官网链接: https://docs.docker.com/engine/install/ubuntu/ 1、运行以下命令卸载所有冲突的软件包: for pkg in docker.io docker-doc docker-compose docker-compose-v2 podman-docker containerd runc; do sudo apt-get remove $pkg; done2、设置Docker…...

Spring AI与Spring Modulith核心技术解析
Spring AI核心架构解析 Spring AI(https://spring.io/projects/spring-ai)作为Spring生态中的AI集成框架,其核心设计理念是通过模块化架构降低AI应用的开发复杂度。与Python生态中的LangChain/LlamaIndex等工具类似,但特别为多语…...
)
.Net Framework 4/C# 关键字(非常用,持续更新...)
一、is 关键字 is 关键字用于检查对象是否于给定类型兼容,如果兼容将返回 true,如果不兼容则返回 false,在进行类型转换前,可以先使用 is 关键字判断对象是否与指定类型兼容,如果兼容才进行转换,这样的转换是安全的。 例如有:首先创建一个字符串对象,然后将字符串对象隐…...
)
安卓基础(aar)
重新设置java21的环境,临时设置 $env:JAVA_HOME "D:\Android Studio\jbr" 查看当前环境变量 JAVA_HOME 的值 echo $env:JAVA_HOME 构建ARR文件 ./gradlew :private-lib:assembleRelease 目录是这样的: MyApp/ ├── app/ …...

Go语言多线程问题
打印零与奇偶数(leetcode 1116) 方法1:使用互斥锁和条件变量 package mainimport ("fmt""sync" )type ZeroEvenOdd struct {n intzeroMutex sync.MutexevenMutex sync.MutexoddMutex sync.Mutexcurrent int…...

从 GreenPlum 到镜舟数据库:杭银消费金融湖仓一体转型实践
作者:吴岐诗,杭银消费金融大数据应用开发工程师 本文整理自杭银消费金融大数据应用开发工程师在StarRocks Summit Asia 2024的分享 引言:融合数据湖与数仓的创新之路 在数字金融时代,数据已成为金融机构的核心竞争力。杭银消费金…...

云原生周刊:k0s 成为 CNCF 沙箱项目
开源项目推荐 HAMi HAMi(原名 k8s‑vGPU‑scheduler)是一款 CNCF Sandbox 级别的开源 K8s 中间件,通过虚拟化 GPU/NPU 等异构设备并支持内存、计算核心时间片隔离及共享调度,为容器提供统一接口,实现细粒度资源配额…...

加密通信 + 行为分析:运营商行业安全防御体系重构
在数字经济蓬勃发展的时代,运营商作为信息通信网络的核心枢纽,承载着海量用户数据与关键业务传输,其安全防御体系的可靠性直接关乎国家安全、社会稳定与企业发展。随着网络攻击手段的不断升级,传统安全防护体系逐渐暴露出局限性&a…...
