Day05 04-MySQL分库分表介绍
文章目录
- 第十七章 MySQL分库分表
- 17.1 什么是分库分表
- 17.2 为什么要分库分表
- 17.3 垂直切分
- 17.3.1 垂直分库
- 17.3.2 垂直分表
- 17.4 水平切分
- 17.4.1 水平分库
- 17.4.2 水平分表
- 17.4.3 常见的水平切分规则
第十七章 MySQL分库分表
17.1 什么是分库分表
MySQL数据库常见的优化方案中,有一种方案就是“分库分表”。那么什么叫“分库分表”呢?其实“分库分表”,从名字上就可以理解是什么意思:
-
分库:将一个数据库拆分成若干数据库,其中的表分布到不同的数据库中。
-
分表:将一个表拆分成若干的小表,其中的数据分布在多张表中。
一个大的数据库可以拆分成为小个数据库,一个大的表也可以拆分成为若干个小的表。拆分之后得到的小的数据库、小的表中的数据量肯定会变少,这样就可以在一定程度上提升查询时候的效率。
17.2 为什么要分库分表
在企业中,随着时间的积累和用户的积累,数据库中的数据量会变得越来越大。如果一张表中的数据量变得非常的庞大了,例如有数千万行数据,此时在这张表中查询数据的时候,将会变得非常的慢。而且,如果这个时候涉及到了多表的联合查询,将会更加耗时,甚至对于性能不高的机器来说,可能还会直接卡死。
因此,我们就需要对这些数据表“减负”,将一个数据库中的数据,分布到多个数据库中存储;将一张表中的数据,分布到多张表中存储。这样可以有效地减少单个表中的数据量,从而达到提高查询效率的目的。
在进行库表切分的时候,常见的有两种方式来实现:垂直切分 和 水平切分。
17.3 垂直切分
17.3.1 垂直分库
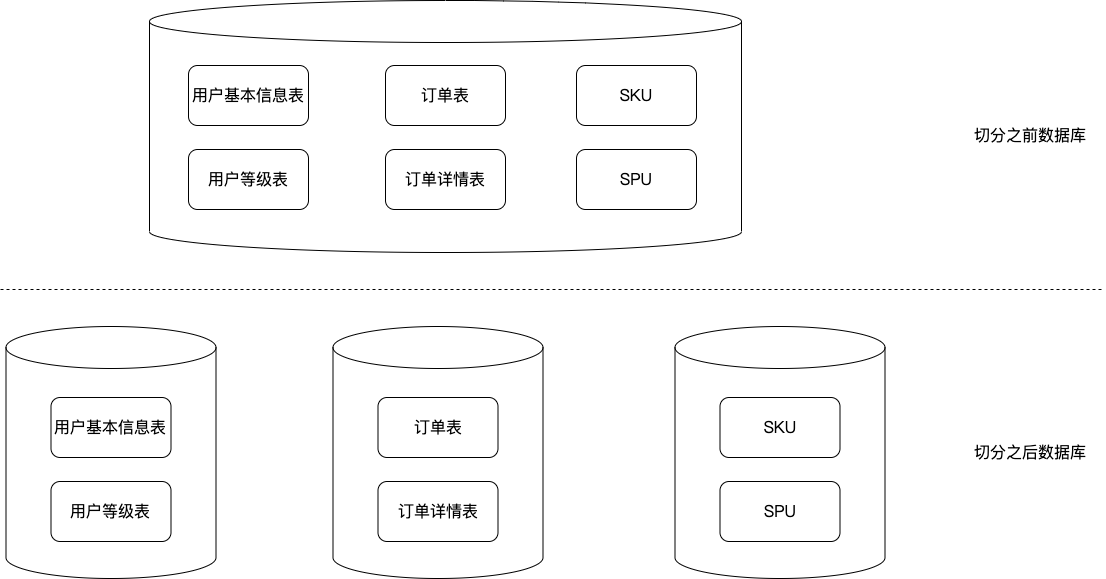
垂直分库就是将一个数据库中的表,拆分到多个切分之后的数据库中。在拆分的时候,需要以表为切分的依据,按照不同的业务场景,将数据表拆分到不同的数据库中。
如下图所示:
切分之前的数据库中,涵盖的数据太多、太复杂,一个电商系统中很多的业务场景下用到的数据表,都在一个数据库中。如果需要对这样的数据库进行垂直切分,需要首先提炼出不同的业务场景,例如用户信息的数据库、商品信息的数据库、订单信息的数据库。然后将原来数据库中的表,根据业务场景,拆分到不同的数据库中即可。
例如:订单表、订单详情表,这些都是与订单相关联的数据,就可以将它们拆分到订单数据库中。
17.3.2 垂直分表
垂直分表就是将一个数据表中的数据,拆分到多个切分之后的数据表中。在拆分的时候,需要以字段为切分的依据,将不同属性的字段拆分到不同的数据表中。
如下图所示:
原来的学生表中的字段非常的多,涵盖的学生的信息也非常的全面。但是这些字段其实是可以分为不同的属性的,在需要垂直分表的时候,就可以将这样的数据表,按照不同的字段属性,对表进行拆分。
例如:sid、sname、age、gender都是属于学生的基本信息的,可以将其拆分到学生基本信息表中。

17.4 水平切分
17.4.1 水平分库
水平分库就是将一个数据库中的表,拆分到多个切分之后的数据库中。在拆分的时候,需要以某字段的值为依据,按照一定的切分规则,将数据拆分到不同的数据库中。切分之后的数据库中每个表的结构都是一样的,但是数据是完全不同的。
17.4.2 水平分表
水平分表就是将一个数据表中的数据,拆分到多个切分之后的数据库中。在拆分的时候,需要以某字段的值为依据,按照一定的切分规则,将数据拆分到不同的数据表中。切分之后每一个表的结构是完全相同的,但是表中的数据是完全不同的。
17.4.3 常见的水平切分规则
-
范围切分:根据指定的字段,切分若干范围,将不同范围的数据切分到不同的表中。
例如:学生表中,主键为sid,且单调递增。
在范围切分的规则中,可以将 [0, 100] 的学生切分到一个表中,[101, 200]的学生切分到一个表中,以此类推。
-
哈希切分:根据指定的字段,根据哈希值,将不同范围的数据切分到不同的表中。
例如:学生表中,主键为sid,且单调递增。
在哈希切分的时候,可以提前制定好需要分的表的数量,用哈希值求模的方式,将数据拆分到不同的表中。
相关文章:

Day05 04-MySQL分库分表介绍
文章目录 第十七章 MySQL分库分表17.1 什么是分库分表17.2 为什么要分库分表17.3 垂直切分17.3.1 垂直分库17.3.2 垂直分表 17.4 水平切分17.4.1 水平分库17.4.2 水平分表17.4.3 常见的水平切分规则 第十七章 MySQL分库分表 17.1 什么是分库分表 MySQL数据库常见的优化方案中…...

基于SpringBoot+vue的毕业生信息招聘平台设计和实现
博主介绍: 大家好,我是一名在Java圈混迹十余年的程序员,精通Java编程语言,同时也熟练掌握微信小程序、Python和Android等技术,能够为大家提供全方位的技术支持和交流。 我擅长在JavaWeb、SSH、SSM、SpringBoot等框架下…...

git一定要学会,加油
gitgit文档http://file:///F:/%E8%B5%84%E6%96%99%E5%A4%8D%E4%B9%A0/Git%E4%BC%98%E7%A7%80%E5%BC%80%E6%BA%90%E4%B9%A6%E7%B1%8D/Git%E5%BC%80%E6%BA%90%E4%B9%A6%E7%B1%8D/Pro%20Git%E4%B8%AD%E6%96%87PDF%E7%89%88.pdf init 初始化仓库 这个命令在当前目录下初始化一个 G…...

TVM面试题
1、TVM中的调度器(Scheduler)是什么?请简要解释TVM调度器的作用和工作原理。 TVM中的调度器(Scheduler)是负责将计算图映射到特定硬件目标上的组件。调度器在TVM中起着关键的作用,它决定了计算图的执行方式、并行化策略以及内存布局等,以优化…...

CSS相关面试题
1、标准盒子模型和IE怪异盒子模型? 标准盒子模型就是指的元素的宽度和高度仅包括的内容区域,不包括边框和内边距,也就是说,元素的实际宽度和高度等于内容区域的宽度和高度IE怪异盒子是指元素的高度和宽度,包括内容区域…...

6.11总结
这周准备了蓝桥杯,主要看了一些以前学过的东西,看了二分,树状数组,树状数组二分,复习了利用倍增相关的算法。 周六去打的蓝桥杯,总体来说也就一般吧,出了考场突然想起来我b题中间的称号写成了加…...
Hazel游戏引擎(008-009)事件系统
文中若有代码、术语等错误,欢迎指正 文章目录 008、事件系统-设计009、事件系统-自定义事件前言自定义事件类与使用声明与定义类代码包含头文件使用事件 事件调度器代码 C知识:FunctionBind用法function基本使用 012、事件系统-DemoLayer用EventDispache…...
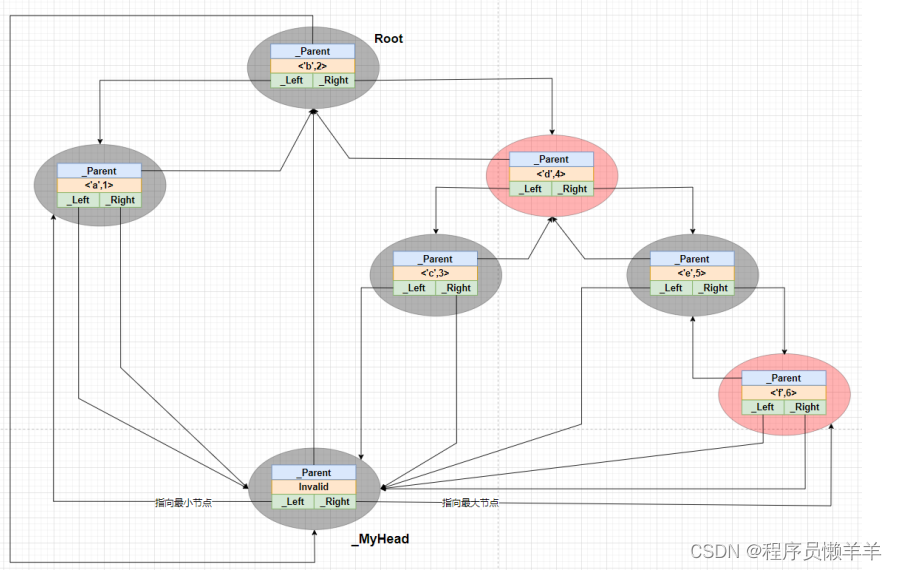
【C++】 STL(上)STL简述、STL容器
文章目录 简述STL容器list链表vector向量deque双端队列map映射表set集合hash_map哈希表 简述 STL是“Standard Template Library”的缩写,中文译为“标准模板库”。STL是C标准库的一部分,位与各个C的头文件中,即他并非以二进制代码的形式提供…...

【002 基础知识】什么是原子操作?
一、原子操作 原子操作就是指不能再进一步分割的操作。 二、为了实现一个互斥,自己定义一个变量作为标记来作为一个资源只有一个使用者行不行? 不行。如果在一个线程正持有锁时(2处),线程上下文发生切换,…...

English Learning - L3 作业打卡 Lesson5 Day32 2023.6.5 周一
English Learning - L3 作业打卡 Lesson5 Day32 2023.6.5 周一 引言🍉句1: What do you read when you are travelling by train or bus?成分划分弱读爆破语调 🍉句2: What are other passengers reading?成分划分弱读连读语调 🍉句3: Perh…...

深度学习应用篇-自然语言处理-命名实体识别[9]:BiLSTM+CRF实现命名实体识别、实体、关系、属性抽取实战项目合集(含智能标注)【上篇】
【深度学习入门到进阶】必看系列,含激活函数、优化策略、损失函数、模型调优、归一化算法、卷积模型、序列模型、预训练模型、对抗神经网络等 专栏详细介绍:【深度学习入门到进阶】必看系列,含激活函数、优化策略、损失函数、模型调优、归一化…...
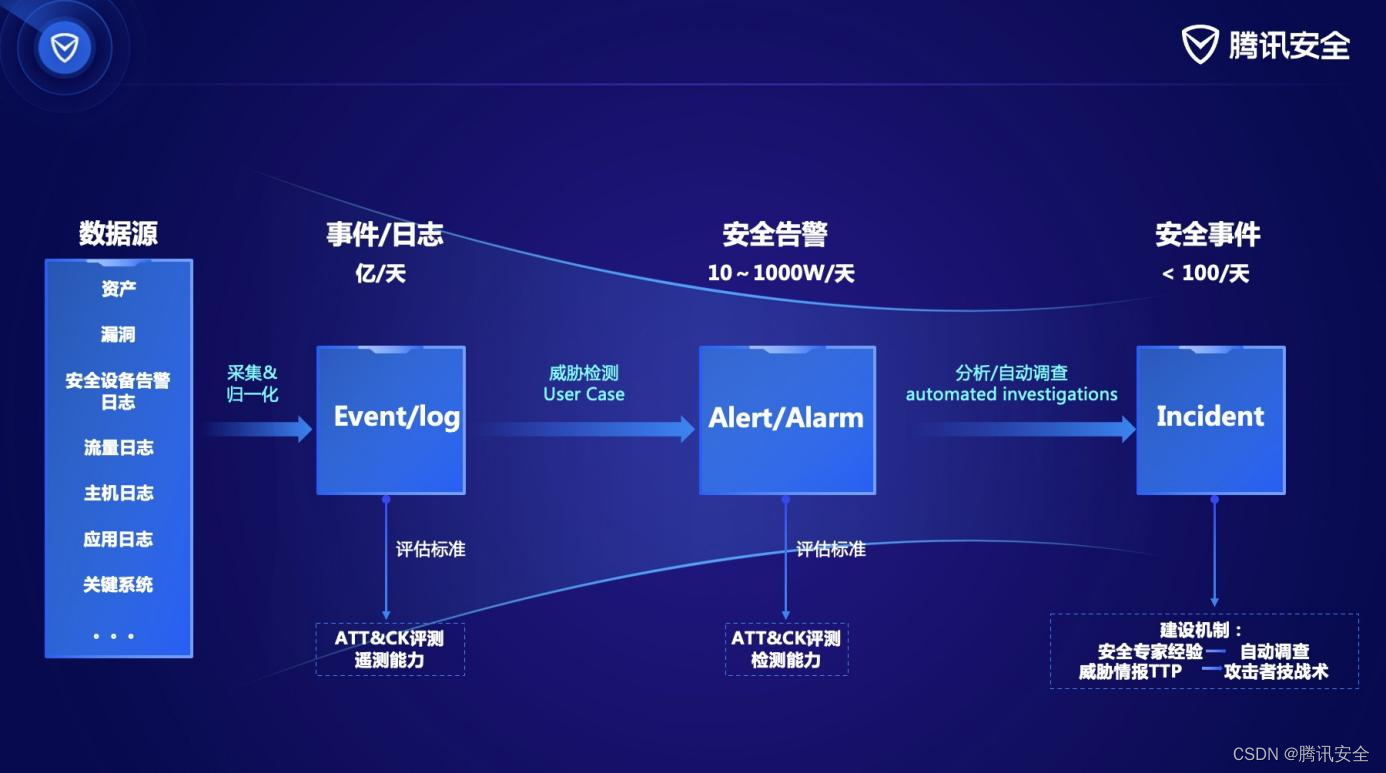
腾讯安全SOC+荣获“鑫智奖”,助力金融业数智化转型
近日,由金科创新社主办,全球金融专业人士协会支持的“2023鑫智奖第五届金融数据智能优秀解决方案评选”榜单正式发布。腾讯安全申报的“SOC基于新一代安全日志大数据平台架构的高级威胁安全治理解决方案”获评“鑫智奖网络信息安全创新优秀解决方案”。 …...

Python绘制气泡图示例
部分数据来源:ChatGPT 引言 在数据可视化领域中,气泡图是一种能够同时展示三维信息的图表类型,常用于表示数据集中的两个变量之间的关系。Python中提供了许多用于绘制气泡图的可视化库,比如pyecharts。在本篇文章中,我们将介绍如何使用pyecharts库绘制一个简单的气泡图,…...

数学建模经历-程序人生
引言 即将大四毕业(现在大三末),闲来无事(为了冲粽子)就写一篇记录数学建模经历的博客吧。其实经常看到一些大佬的博客里会有什么"程序人生"、"人生感想"之类的专栏,但是由于我只是一个小趴菜没什么阅历因此也就没有写过类似的博客…...

数字电子电路绪论
博主介绍:一个爱打游戏的计算机专业学生 博主主页:夏驰和徐策 所属专栏:程序猿之数字电路 1.科技革命促生互联网时代 科技革命对互联网时代的兴起产生了巨大的推动作用。以下是一些科技革命对互联网时代的促进因素: 1. 计算机技…...

电脑丢失dll文件一键修复需要什么软件?快速修复dll文件的方法
在使用电脑的过程中,我们经常会遇到程序无法正常运行的情况,提示“XXX.dll文件丢失”的错误。这时候,很多人会感到困惑,不知道该如何解决。本文将详细介绍dll文件丢失的各种原因、如何使用dll修复工具进行一键修复dll丢失问题以及…...
你知道微信的转账是可以退回的吗
微信作为当今最受欢迎的即时通讯软件之一,其转账功能得到了广泛的应用。在使用微信转账时,我们可能会遇到一些问题,例如误操作、支付失败或者需要退款等等。 首先需要注意的是,微信转账退回的操作只能在“一天内未确认”时进行。如…...
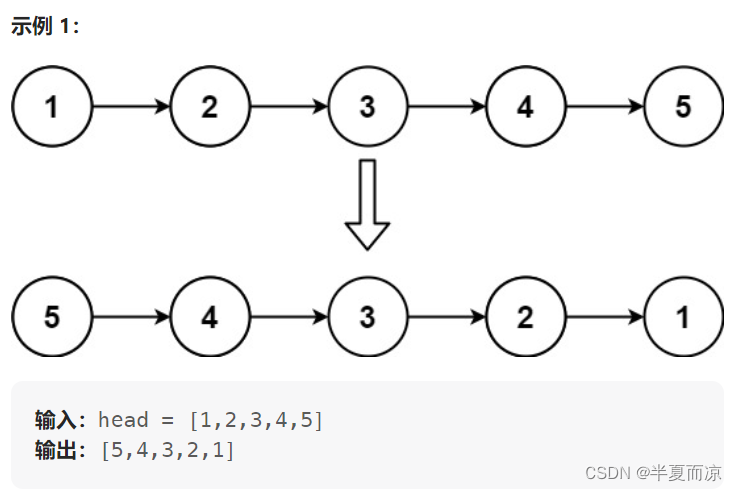
【链表Part01】| 203.移除链表元素、707.设计链表、206.反转链表
目录 ✿LeetCode203.移除链表元素❀ ✿LeetCode707.设计链表❀ ✿LeetCode206.反转链表❀ ✿LeetCode203.移除链表元素❀ 链接:203.移除链表元素 给你一个链表的头节点 head 和一个整数 val ,请你删除链表中所有满足 Node.val val 的节点ÿ…...

如何使用Postman生成curl?
生成在Lunix系统调接口的curl 直接看图操作 点击</>即可!...

CSS灯光效果,背景黑金效果
先看效果 再看代码: <!DOCTYPE html> <html lang"en"> <head><meta charset"UTF-8"><title>灯光效果</title><link href"https://fonts.googleapis.com/css2?familyCinzel:wght700&dis…...

装饰模式(Decorator Pattern)重构java邮件发奖系统实战
前言 现在我们有个如下的需求,设计一个邮件发奖的小系统, 需求 1.数据验证 → 2. 敏感信息加密 → 3. 日志记录 → 4. 实际发送邮件 装饰器模式(Decorator Pattern)允许向一个现有的对象添加新的功能,同时又不改变其…...

C++_核心编程_多态案例二-制作饮品
#include <iostream> #include <string> using namespace std;/*制作饮品的大致流程为:煮水 - 冲泡 - 倒入杯中 - 加入辅料 利用多态技术实现本案例,提供抽象制作饮品基类,提供子类制作咖啡和茶叶*//*基类*/ class AbstractDr…...

【Oracle APEX开发小技巧12】
有如下需求: 有一个问题反馈页面,要实现在apex页面展示能直观看到反馈时间超过7天未处理的数据,方便管理员及时处理反馈。 我的方法:直接将逻辑写在SQL中,这样可以直接在页面展示 完整代码: SELECTSF.FE…...

oracle与MySQL数据库之间数据同步的技术要点
Oracle与MySQL数据库之间的数据同步是一个涉及多个技术要点的复杂任务。由于Oracle和MySQL的架构差异,它们的数据同步要求既要保持数据的准确性和一致性,又要处理好性能问题。以下是一些主要的技术要点: 数据结构差异 数据类型差异ÿ…...

DeepSeek 技术赋能无人农场协同作业:用 AI 重构农田管理 “神经网”
目录 一、引言二、DeepSeek 技术大揭秘2.1 核心架构解析2.2 关键技术剖析 三、智能农业无人农场协同作业现状3.1 发展现状概述3.2 协同作业模式介绍 四、DeepSeek 的 “农场奇妙游”4.1 数据处理与分析4.2 作物生长监测与预测4.3 病虫害防治4.4 农机协同作业调度 五、实际案例大…...

【数据分析】R版IntelliGenes用于生物标志物发现的可解释机器学习
禁止商业或二改转载,仅供自学使用,侵权必究,如需截取部分内容请后台联系作者! 文章目录 介绍流程步骤1. 输入数据2. 特征选择3. 模型训练4. I-Genes 评分计算5. 输出结果 IntelliGenesR 安装包1. 特征选择2. 模型训练和评估3. I-Genes 评分计…...

【分享】推荐一些办公小工具
1、PDF 在线转换 https://smallpdf.com/cn/pdf-tools 推荐理由:大部分的转换软件需要收费,要么功能不齐全,而开会员又用不了几次浪费钱,借用别人的又不安全。 这个网站它不需要登录或下载安装。而且提供的免费功能就能满足日常…...

C/C++ 中附加包含目录、附加库目录与附加依赖项详解
在 C/C 编程的编译和链接过程中,附加包含目录、附加库目录和附加依赖项是三个至关重要的设置,它们相互配合,确保程序能够正确引用外部资源并顺利构建。虽然在学习过程中,这些概念容易让人混淆,但深入理解它们的作用和联…...

Mysql8 忘记密码重置,以及问题解决
1.使用免密登录 找到配置MySQL文件,我的文件路径是/etc/mysql/my.cnf,有的人的是/etc/mysql/mysql.cnf 在里最后加入 skip-grant-tables重启MySQL服务 service mysql restartShutting down MySQL… SUCCESS! Starting MySQL… SUCCESS! 重启成功 2.登…...
免费数学几何作图web平台
光锐软件免费数学工具,maths,数学制图,数学作图,几何作图,几何,AR开发,AR教育,增强现实,软件公司,XR,MR,VR,虚拟仿真,虚拟现实,混合现实,教育科技产品,职业模拟培训,高保真VR场景,结构互动课件,元宇宙http://xaglare.c…...
