找到距离最近的点,性能最好的方法
要找到距离最近的点并且性能最好,一种常用的方法是使用空间数据结构来加速搜索过程。以下是两个常见的数据结构和它们的应用:
- KD树(KD-Tree):KD树是一种二叉树数据结构,用于对k维空间中的点进行分割和组织。它可以有效地支持最近邻搜索。在构建KD树时,将点递归地划分为左右子树,使每个节点代表一个超矩形区域。在搜索时,可以根据目标点的位置逐级向下搜索树的分支,从而减少搜索的次数和范围。KD树的构建和搜索操作的时间复杂度为O(log n),其中n是点的数量。
- 四叉树(Quadtree):四叉树是一种分割二维空间的树形数据结构。它将空间划分为四个象限,并递归地划分每个象限,直到达到终止条件。在每个节点上存储点的引用或密度信息。通过四叉树,可以将空间划分为不同的层级,从而快速定位和搜索最近的点。四叉树的构建和搜索操作的时间复杂度为O(log n),其中n是点的数量。
这些空间数据结构可以根据实际需求选择和实现。构建数据结构的时间复杂度可能较高,但在之后的最近邻搜索过程中可以快速找到最近的点,从而提高性能。请注意,对于非常大的数据集,您可能还需要考虑使用更高级的数据结构或算法来进一步优化搜索效率。
另外,如果点的数量不是非常大,你也可以使用简单的遍历方法,在遍历过程中计算并更新最近的点。这种方法的时间复杂度为O(n),其中n是点的数量。虽然这种方法的性能较差,但对于小规模的数据集可能是足够的。
怎么实现KD树
实现KD树可以是一个复杂的任务,涉及到树的构建、插入和搜索等操作。下面是一个简单的KD树的实现示例,展示了构建、插入和最近邻搜索的基本思路:
using UnityEngine;
using System.Collections.Generic;public class KdTree
{private class KdTreeNode{public Vector3 position;public KdTreeNode left;public KdTreeNode right;public KdTreeNode(Vector3 position){this.position = position;left = null;right = null;}}private KdTreeNode root;public void Insert(Vector3 position){root = InsertRecursive(root, position, 0);}private KdTreeNode InsertRecursive(KdTreeNode node, Vector3 position, int depth){if (node == null){return new KdTreeNode(position);}int axis = depth % 3; // 3维空间,根据深度选择切分轴if (position[axis] < node.position[axis]){node.left = InsertRecursive(node.left, position, depth + 1);}else{node.right = InsertRecursive(node.right, position, depth + 1);}return node;}public KdTreeNode FindNearest(Vector3 targetPosition){if (root == null){return null;}KdTreeNode nearestNode = null;float nearestDistance = float.MaxValue;FindNearestRecursive(root, targetPosition, 0, ref nearestNode, ref nearestDistance);return nearestNode;}private void FindNearestRecursive(KdTreeNode node, Vector3 targetPosition, int depth, ref KdTreeNode nearestNode, ref float nearestDistance){if (node == null){return;}float distance = Vector3.Distance(node.position, targetPosition);if (distance < nearestDistance){nearestNode = node;nearestDistance = distance;}int axis = depth % 3; // 3维空间,根据深度选择切分轴if (targetPosition[axis] < node.position[axis]){FindNearestRecursive(node.left, targetPosition, depth + 1, ref nearestNode, ref nearestDistance);// 检查是否需要在另一个子树搜索if (Mathf.Abs(targetPosition[axis] - node.position[axis]) < nearestDistance){FindNearestRecursive(node.right, targetPosition, depth + 1, ref nearestNode, ref nearestDistance);}}else{FindNearestRecursive(node.right, targetPosition, depth + 1, ref nearestNode, ref nearestDistance);// 检查是否需要在另一个子树搜索if (Mathf.Abs(targetPosition[axis] - node.position[axis]) < nearestDistance){FindNearestRecursive(node.left, targetPosition, depth + 1, ref nearestNode, ref nearestDistance);}}}
}
在上述代码中,我们定义了一个内部类KdTreeNode来表示KD树的节点,每个节点包含一个位置position、左子节点left和右子节点right。
构建KD树的过程通过递归的方式实现,使用InsertRecursive函数在树中插入新的节点。在每个节点上,我们根据当前的深度选择切分轴,并根据切分轴的值将新的节点插入到左子树或右子树中。
最近邻搜索的过程也是通过递归实现的,使用FindNearestRecursive函数来查找最近的节点。在每个节点上,我们计算目标位置与当前节点位置的距离,并更新最近节点和最近距离。然后,根据当前深度和切分轴的值,选择在左子树或右子树中进一步搜索,同时根据距离当前切分轴的距离,确定是否需要在另一个子树中搜索。
请注意,上述代码是一个简化的KD树实现,仅展示了基本的构建、插入和最近邻搜索的思路。对于更复杂的应用,可能需要考虑更多的细节和优化。此外,这里的KD树实现是针对3维空间的情况,如果需要处理其他维度的数据,需要进行相应的调整。
如果你希望使用更完整和高性能的KD树实现,建议查找现有的KD树库或参考更详细的教程和文档来实现。
相关文章:

找到距离最近的点,性能最好的方法
要找到距离最近的点并且性能最好,一种常用的方法是使用空间数据结构来加速搜索过程。以下是两个常见的数据结构和它们的应用: KD树(KD-Tree):KD树是一种二叉树数据结构,用于对k维空间中的点进行分割和组织…...

vue基础--重点
!1、vue的特性 !2、v-model 双向数据绑定指令 (data数据源变化,页面变化; 页面变化,data数据源也变化) 1、v-model 会感知到 框中数据变化 2、v-model 只有在表单元素中使用,才能…...

HarmonyOS元服务端云一体化开发快速入门(上)
一、前提条件 您已使用已实名认证的华为开发者帐号登录DevEco Studio。 请确保您的华为开发者帐号余额充足,账户欠费将导致云存储服务开通失败。 二、选择云开发模板 1.选择以下任一种方式,打开工程创建向导界面。 如果当前未打开任何工程,…...
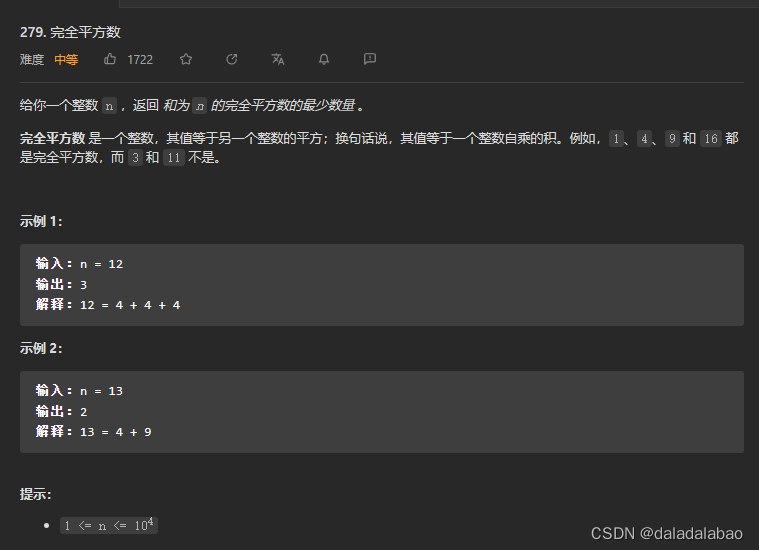
leetcode 279.完全平方数
题目描述 给你一个整数 n ,返回 和为 n 的完全平方数的最少数量 。 完全平方数 是一个整数,其值等于另一个整数的平方;换句话说,其值等于一个整数自乘的积。例如,1、4、9 和 16 都是完全平方数,而 3 和 11 …...

Spring boot ApplicationContext
https://www.geeksforgeeks.org/spring-applicationcontext/ AnnotationConfigApplicationContext container 对象直接标注annotation: Configuration, Component ApplicationContext context new AnnotationConfigApplicationContext(AppConfig.class, AppConf…...

【Python实战】Python采集王者皮肤图片
前言 我们上一篇介绍了,如何采集王者最低战力,本文就来给大家介绍如何采集王者皮肤,买不起皮肤,当个桌面壁纸挺好的。下面,我和大家介绍如何获取数据。 环境使用 python 3.9pycharm 模块使用 requests 模块介绍 re…...
很详细的Django开发入门详解(图文并茂)
1.Django概述 Django是一个开放源代码的Web应用框架,由Python写成。采用了MTV的框架模式,即模型M,视图V和模版T。 Django 框架的核心组件有: 用于创建模型的对象关系映射;为最终用户设计较好的管理界面;…...

Ansible 部署
ansible 自动化运维工具,可以实现批量管理多台(成百上千)主机,应用级别的跨主机编排工具 特性: 无agent的存在,不要在被控制节点上安装客户端应用 通过ssh协议与被控制节点通信 基于模块工作的,…...
【操作系统】计算机操作系统知识点总结
文章目录 前言一、操作系统的概念与发展二、操作系统的结构与功能1、操作系统的结构2、操作系统的功能 三、进程管理1、进程2、进程的创建3、进程管理的实现4、进程控制块 四、内存管理1、内存2、内存管理3、内存管理的实现 五、文件系统1、文件系统2、文件系统的主要任务3、文…...

springmvc整合thymeleaf
概述 Thymeleaf提供了一组Spring集成,使您可以将其用作Spring MVC应用程序中JSP的全功能替代品。 这些集成将使您能够: Controller像使用JSP一样,将Spring MVC 对象中的映射方法转发到Thymeleaf管理的模板。在模板中使用Spring表达式语言&…...

Redis 内存管理机制
Redis作为一个内存数据库,内存资源非常珍贵。因此,Redis引入了3种内存管理机制来释放不必要的内存,包括定期删除、惰性删除和内存淘汰机制。 定期删除 定期删除是Redis内存管理机制的一种,它用于删除过期的键值对。Redis每隔 10…...
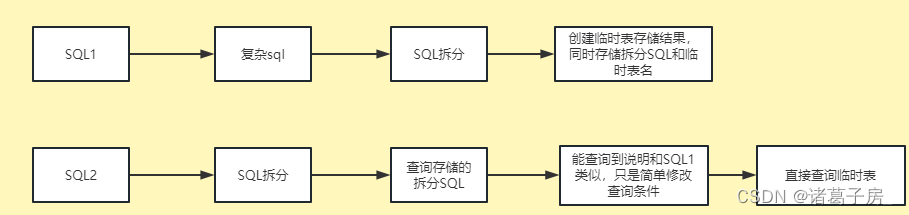
Apache Zeppelin系列教程第九篇——Zeppelin NoteBook数据缓存
背景 在使用Zeppelin JDBC Intercepter 对于Hive 数据进行查询过程中,如果遇到非常复杂的sql,查询效率是非常慢 比如: select dt,count(*) from table group by dt做过数据开发的同学都知道,在hive sql查询过程中,hive…...

用代码实现一个简单计算器
作者主页:paper jie的博客_CSDN博客-C语言,算法详解领域博主 本文作者:大家好,我是paper jie,感谢你阅读本文,欢迎一建三连哦。 本文录入于《C语言》专栏,本专栏是针对于大学生,编程小白精心打造…...

运维圣经:挖矿木马应急响应指南
目录 挖矿木马简介 挖矿流程 挖矿木马应急响应 一. 隔离被感染主机 二. 确定挖矿进程 三. 挖矿木马清除 1、阻断矿池地址的连接 2、清除挖矿定时任务、启动项等 3、禁用可疑用户 4、定位挖矿木马文件的位置并删除 5、全盘杀毒、加固 挖矿木马简介 挖矿:…...
【Flutter】Flutter 如何获取安装来源信息
文章目录 一、 前言二、 安装来源信息的基本概念1. 什么是安装来源信息2. 为什么我们需要获取安装来源信息 三、 如何在 Flutter 中获取安装来源信息1. 准备工作2. 安装必要的依赖库3. 编写代码获取安装来源信息 四、 完整示例代码五、总结 一、 前言 在这篇文章中,…...
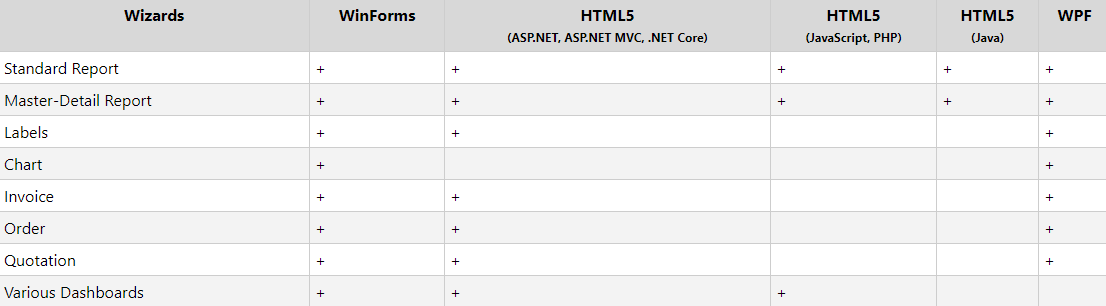
Stimulsoft Reports用户手册:Report Designer介绍
Stimulsoft Reports.Net是一个基于.NET框架的报表生成器,能够帮助你创建结构、功能丰富的报表。StimulReport.Net 的报表设计器不仅界面友好,而且使用便捷,能够让你轻松创建所有报表;该报表设计器在报表设计过程中以及报表运行的过…...
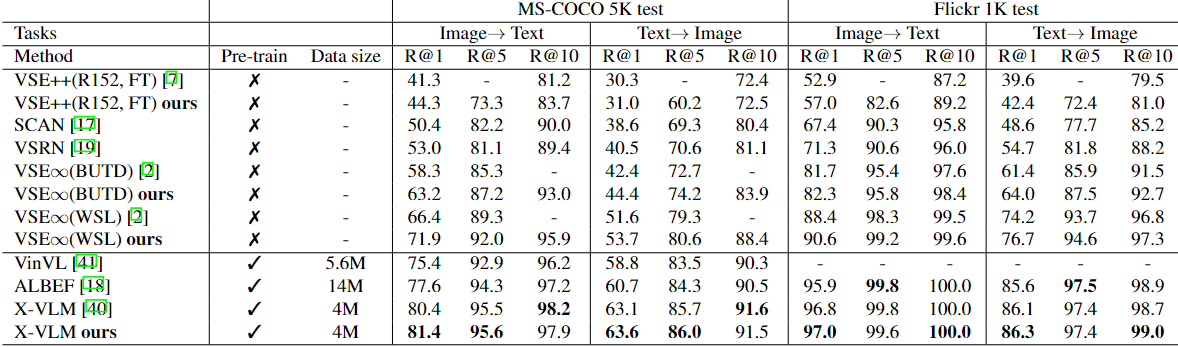
跨模态检索论文阅读:Dissecting Deep Metric Learning Losses for Image-Text Retrieval(GOAL)
Dissecting Deep Metric Learning Losses for Image-Text Retrieval 剖析图像文本检索中的深度度量学习损失 2022.10 视觉语义嵌入(VSE)是图像-文本检索中的一种流行的应用方法,它通过学习图像和语言模式之间的联合嵌入空间来保留语义的相似性…...

贪心算法part5 | ● 435. 无重叠区间 ● 763.划分字母区间 ● 56. 合并区间
文章目录 435. 无重叠区间思路思路代码困难 763.划分字母区间思路官方题解代码困难 56. 合并区间思路思路代码 今日收获 435. 无重叠区间 思路 重叠问题都需要先排好序,再贪心 思路代码 func eraseOverlapIntervals(intervals [][]int) int {sort.Slice(interva…...
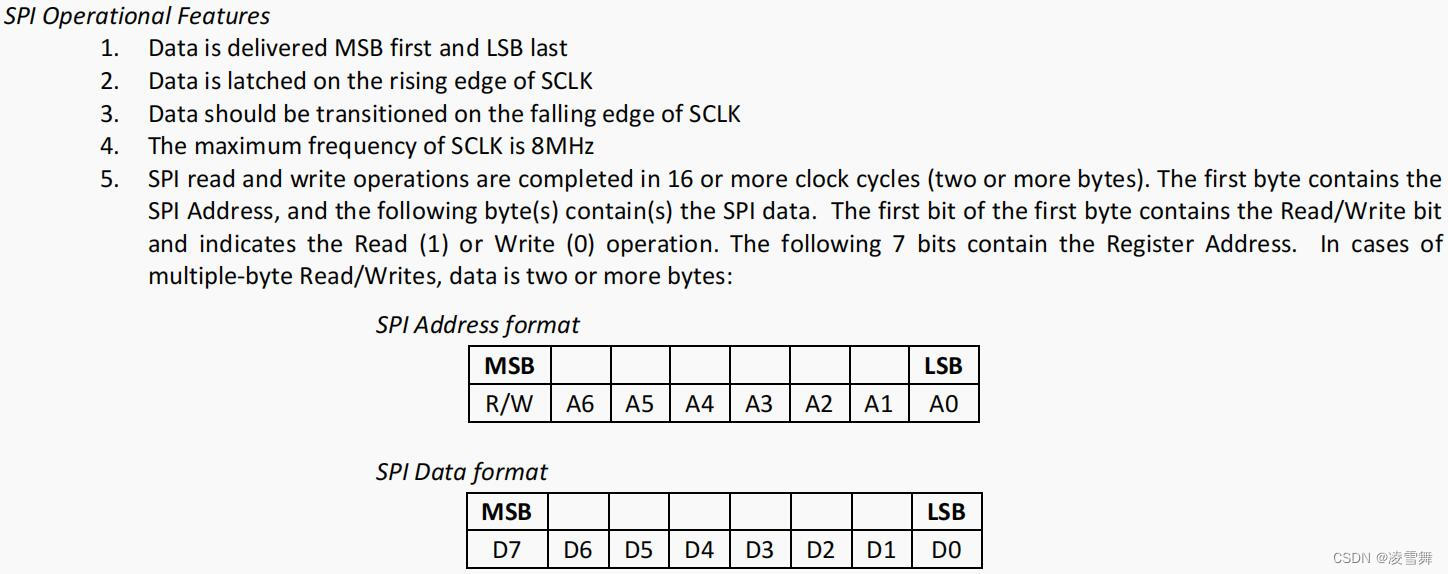
IMX6ULL裸机篇之SPI实验-ICM20608代码实现
一. SPI 实验 SPI实验:学习如何使用 I.MX6U 的 SPI 接口来驱动 ICM-20608,读取 ICM-20608 的六轴数据。 本文学习 SPI通信实验中,涉及从设备的 SPI代码编写。 之前学习了 SPI 主控芯片代码的编写,如下所示: IMX6ULL…...

51单片机读取DS18B20温度传感器
1.首先我们知道DS18B20是单总线协议,只有一根数据线。所以Data数据线即使发送端又是接收端,同时DS18B20内部接了弱上拉电阻(如图一所示),数据线默认为高电平。有了这些概念,我们就能进行下一步。 图一&…...

未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?
编辑:陈萍萍的公主一点人工一点智能 未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?RWM通过双自回归机制有效解决了复合误差、部分可观测性和随机动力学等关键挑战,在不依赖领域特定归纳偏见的条件下实现了卓越的预测准…...

ESP32读取DHT11温湿度数据
芯片:ESP32 环境:Arduino 一、安装DHT11传感器库 红框的库,别安装错了 二、代码 注意,DATA口要连接在D15上 #include "DHT.h" // 包含DHT库#define DHTPIN 15 // 定义DHT11数据引脚连接到ESP32的GPIO15 #define D…...

Python 包管理器 uv 介绍
Python 包管理器 uv 全面介绍 uv 是由 Astral(热门工具 Ruff 的开发者)推出的下一代高性能 Python 包管理器和构建工具,用 Rust 编写。它旨在解决传统工具(如 pip、virtualenv、pip-tools)的性能瓶颈,同时…...

九天毕昇深度学习平台 | 如何安装库?
pip install 库名 -i https://pypi.tuna.tsinghua.edu.cn/simple --user 举个例子: 报错 ModuleNotFoundError: No module named torch 那么我需要安装 torch pip install torch -i https://pypi.tuna.tsinghua.edu.cn/simple --user pip install 库名&#x…...

使用Spring AI和MCP协议构建图片搜索服务
目录 使用Spring AI和MCP协议构建图片搜索服务 引言 技术栈概览 项目架构设计 架构图 服务端开发 1. 创建Spring Boot项目 2. 实现图片搜索工具 3. 配置传输模式 Stdio模式(本地调用) SSE模式(远程调用) 4. 注册工具提…...

uniapp手机号一键登录保姆级教程(包含前端和后端)
目录 前置条件创建uniapp项目并关联uniClound云空间开启一键登录模块并开通一键登录服务编写云函数并上传部署获取手机号流程(第一种) 前端直接调用云函数获取手机号(第三种)后台调用云函数获取手机号 错误码常见问题 前置条件 手机安装有sim卡手机开启…...

并发编程 - go版
1.并发编程基础概念 进程和线程 A. 进程是程序在操作系统中的一次执行过程,系统进行资源分配和调度的一个独立单位。B. 线程是进程的一个执行实体,是CPU调度和分派的基本单位,它是比进程更小的能独立运行的基本单位。C.一个进程可以创建和撤销多个线程;同一个进程中…...

c++第七天 继承与派生2
这一篇文章主要内容是 派生类构造函数与析构函数 在派生类中重写基类成员 以及多继承 第一部分:派生类构造函数与析构函数 当创建一个派生类对象时,基类成员是如何初始化的? 1.当派生类对象创建的时候,基类成员的初始化顺序 …...

WebRTC从入门到实践 - 零基础教程
WebRTC从入门到实践 - 零基础教程 目录 WebRTC简介 基础概念 工作原理 开发环境搭建 基础实践 三个实战案例 常见问题解答 1. WebRTC简介 1.1 什么是WebRTC? WebRTC(Web Real-Time Communication)是一个支持网页浏览器进行实时语音…...

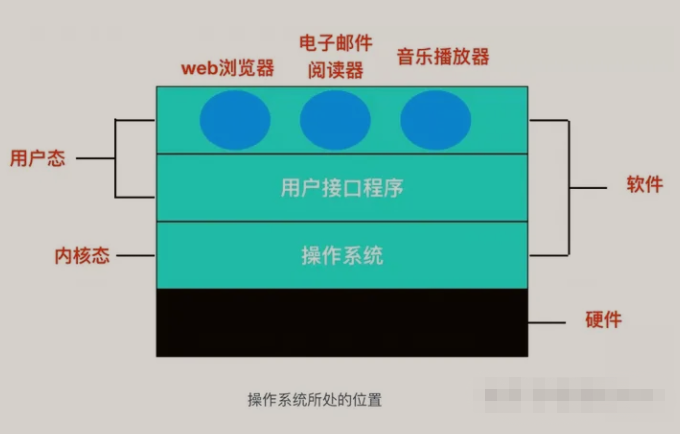
【Linux手册】探秘系统世界:从用户交互到硬件底层的全链路工作之旅
目录 前言 操作系统与驱动程序 是什么,为什么 怎么做 system call 用户操作接口 总结 前言 日常生活中,我们在使用电子设备时,我们所输入执行的每一条指令最终大多都会作用到硬件上,比如下载一款软件最终会下载到硬盘上&am…...
