数据结构练习题1:基本概念
练习题1:基本概念
- 1 抽象数据类型概念分析
- 2. 逻辑结构与存储结构概念分析
- 3.综合选择题
- 4.综合判断题
- 5.时间复杂度相关习题
- 6 时间复杂度计算方法(一、二、三层循环)
1 抽象数据类型概念分析
1.可以用(抽象数据类型)定义一个完整的数据结构。
分析:
1)抽象数据类型(ADT)描述了数据的逻辑结构和抽象运算,通常用数据对象、数据关系和基本操作集这样的三元组来表示,从而构成一个完整的数据结构定义。
2)抽象数据类型的两个重要特征:数据抽象和数据封装。
①数据抽象:用ADT描述程序处理的实体时,强调的是其本质的特征、其所能完成的功能以及它和外部用户的接口。(即外界使用它的方法)
②数据封装:将实体的外部特性和其内部实现细节分离,并且对外部用户隐藏其内部实现细节。
抽象数据类型的理解
2. 逻辑结构与存储结构概念分析
1.数据的逻辑结构独立于其存储结构。
分析:数据的逻辑结构从实际问题出发,只采用抽象表达方式,独立于存储结构,数据的存储方式有多种选择。而数据的存储结构是逻辑结构在计算机上的映射,它不能独立于逻辑结构而存在。
2.数据结构的三要素:逻辑结构、存储结构和运算。
问题:逻辑结构的存储方式有多种选择什么意思?
是指既能顺序存储又能链式存储。
3.下面属于逻辑结构的是
A 顺序表 B 哈希表 C 有序表 D 单链表
4.以下与数据的存储结构有关的术语是
A.有序表 B.线性表 C.有向图 D.顺序表
5.以下与数据的存储结构无关的术语是
A 循环队列 B 链表 C 哈希表 D 栈
逻辑结构与存储结构: 3-5 CDD
有序表、线性表、有向图既能顺序存储,又能链式存储,是逻辑结构。
顺序表、循环队列、顺序栈为顺序存储。
属于逻辑结构 = 与存储结构无关 = 既能顺序存储又能链式存储
与存储结构有关 = 只能顺序存储或只能链式存储
栈逻辑结构对应的顺序存储结构为顺序栈,对应的链式存储结构为链栈。
队列的顺序存储结构是循环队列,链式存储结构是链队列,又叫做单链表。
线性表逻辑结构对应的顺序存储结构为顺序表,对应的链式存储结构为链表。
特殊案例:
有序表是指关键字有序的线性表,仅描述元素之间的逻辑关系,既可以顺序存储(使用数组)也可以链式存储(使用指针),不受存储结构制约,由于有序受到逻辑制约,属于逻辑结构。
哈希表,是个大数组,顺序存储。
问题1:如何区分数据结构和数据类型?
数据类型的运算主要是算数运算、逻辑运算等。
而数据结构运算主要是对数据的增删改查等。
数据类型和数据结构的区别
问题2:抽象数据类型有哪些?
栈、队列、树、图、集合、映射。
问题3:哈希表是散列存储,为什么做题时不考虑这种存储方式?
6.存储数据时存储的是数据元素的值和数据元素之间的关系。
7.链式存储设计时,各个不同结点存储空间可以不连续,但结点内的存储单元地址必须连续。
结点内什么意思? 是value值域与next域结合,称这个结点为内部。typedef struct LNode {
int value; // value中存放结点值域,默认是int型
struct Lnode *next;//指向后继结点的指针
}LNode; // 定义单链表结点类型
上述定义了一个结构体,包括两部分,一是值域,二是指针域;每当定义一个结点都会产生这两个区域。如下图:
| value | next |
|---|
这个value与next域必须是挨着的,称这个结点为内部。
结点内部一定是连续的。若第一个结点占用两个地址,那么value域的起始地址是1,则指针域的地址就是2。同理若第二个结点的value地址是10,则next域就是11。
参考:链式存储设计时,链表结点内的存储单元地址是如何分布的
3.综合选择题
1.下列叙述中正确的是
A)算法的效率只与问题的规模有关,而与数据的存储结构无关
B)算法的时间复杂度是指执行算法所需要的计算工作量
C)数据的逻辑结构与存储结构是一一对应的
D)算法的时间复杂度与空间复杂度一定相关
2.算法的有穷性是指
A)算法程序的运行时间是有限的 B)算法程序所处理的数据量是有限的
C)算法程序的长度是有限的 D)算法只能被有限的用户使用
3.下列叙述中正确的是
A)一个逻辑数据结构只能有一种存储结构
B)数据的逻辑结构属于线性结构,存储结构属于非线性结构
C)一个逻辑数据结构可以有多种存储结构,且各种存储结构不影响数据处理的效率
D)一个逻辑数据结构可以有多种存储结构,且各种存储结构影响数据处理的效率
4.算法的空间复杂度是指
A)算法程序的长度 B)算法程序中的指令条数
C)执行算法程序所占的存储空间 D)算法执行过程中所需要的存储空间
5.在下列选项中,哪个不是一个算法一般应该具有的基本特征
A、确定性 B、可行性 C、无穷性 D、拥有足够的情报
6.被计算机加工的数据元素不是孤立的,它们彼此之间一般存在某种关系,通常把数i元素之间的这种关系称为
A 规则 B 结构 C 集合 D 运算
7.设有如下遗产继承规则:丈夫和妻子可以互相继承遗产,子女可以继承父亲和母亲的遗产,子女间不能相互继承,则表示该遗产继承关系最合适的数据结构应该是
A 树 B 图 C 线性表 D 集合
8.下面关于抽象数据类型的描述错误的是
A.数据封装 B.用例驱动
C.信息隐藏 D.使用与实现分离
9.数据结构中,与所使用的计算机无关的是数据的
A 存储结构 B 物理结构 C 逻辑结构 D 物理和存储结构
10.下列关于算法的时间复杂度陈述正确的是
A 算法的时间复杂度是指执行算法程序所需要的时间
B 算法的时间复杂度是指算法程序的长度
C 算法的时间复杂度是指算法执行过程中所需要的基本运算次数
D 算法的时间复杂度是指算法程序中的指令条数
综合选择题:1-5 BADCC 6-10 BBBCC
4.综合判断题
1…在数据元素内数据项之间也有关系,在讨论数据的逻辑结构时应考虑。 × 逻辑结构看的是数据元素之间的关系
2.同一个算法,实现语言级别越高,算法执行的效率越低。√ 级别越高,需要额外执行的条件就越多,效率也就越低。
3.集合中任何两个数据元素之间都没有逻辑关系,而且组织形式松散。√ 除同属于一个集合外,没有其他任何关系。
5.时间复杂度相关习题
O(1)<O(log2n)<O(n)<O(nlog2n)<O( n 2 n^2 n2)<O( n 3 n^3 n3)<O( 2 n 2^n 2n)<O(n!)<O( n n n^n nn)
1.下面时间复杂度较小的是 A
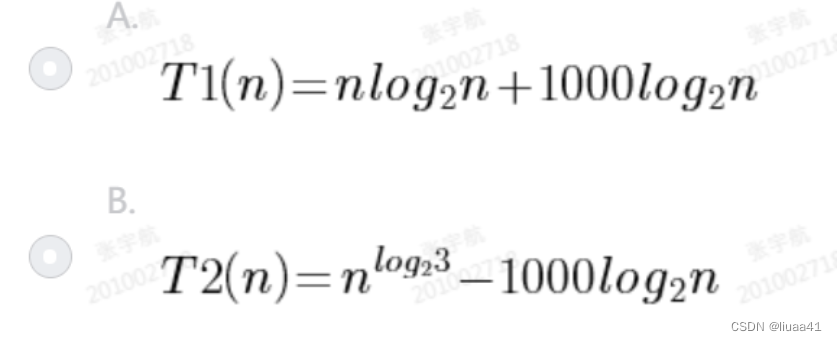
2.以下程序段中语句"m++;"的语句频度为 C
int m=0,i,j;
for(i=1;i<=n;i++)
for(j=1;j<=2*ij++)m++;
A n B n+1 C n(n+1) D n 2 n^2 n2
2+4+6+…+2n = n(n+1)
3.下列函数的时间复杂度是() 。
int func(int n){
int i=0,sum=O;
while(sum<n) sum+=++i;
return i;
}
设语句频度为f(n)
1+2+3+…+f(n)<n
(1+f(n))f(n)/2<n
解得时间复杂度为O(n^(1/2) )
a=i++,这个运算的意思是先把i的值赋予a,然后在执行i=i+1;
a=++i,这个的意思是先执行i=i+1,然后在把i的值赋予a;
4.下面说法错误的是 D
A 某算法的时间复杂度为O( n 2 n^2 n2),表明该算法的执行时间与 n 2 n^2 n2成正比
B 在相同的规模n下,复杂度O(n)的算法在时间上总是优于复杂度O( n 2 n^2 n2)算法
C 所谓时间复杂度是指最坏情况下,估算算法执行时间的一个上界
D 算法原地工作的含义是指不需要任何额外的辅助空间
时间复杂度:一般总是考虑在最坏情况下的时间复杂度,以保证算法的运行时间不会比它更长,即它是最坏情况下估算算法执行时间的一个上界。
算法的时间复杂度只与规模相关吗?
算法的时间复杂度不仅与问题的规模相关,还与输入实例中的初始状态有关。但在最坏的情况下,其时间复杂度就是只与求解问题的规模相关的。我们在讨论时间复杂度时,一般就是以最坏情况下的时间复
杂度为准的。
算法原地工作是指算法所需的辅助空间是常量。
5.下面算法将一维数组a中的n个数逆序存放到原数组中,空间复杂度为()。
for(i=0;i<n/2;i++){
t=a[i];
a[i]=a[n-i-1];
a[n-i-1]=t}
该算法仅需要借助一个变量t,与问题规模n的大小无关,所以其空间复杂度为O(1)
很值得看的理解:
时间复杂度和空间复杂度计算
时间复杂度分析(含王道绪论习题)
6.以下关系式中,错误的是 D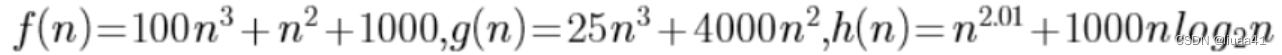
A f(n) =O(g(n))
B g(n) = O(f(n))
C h(n) = O( n 2 n^2 n2)
D h(n) = O(nlog2n)
已知f(n)=O(g(n)),则必能推出g(n)=O(f(n))
7.
A.O(1) B.O(n) C.O( n − 1 n^{-1} n−1) D.O( n 2 n^2 n2)
答案选B n趋与无穷,f(n)/n为常数
8.设n是描述问题规模的非负整数,下列程序段的时间复杂度是 B
x=0;
while(n>=(x+1)*(x+1))
x=x+1;
A.O(logn) B.O( n 1 / 2 n^1/2 n1/2) C.O(n) D.O( n 2 n^2 n2)
9.下列程序段的时间复杂度是
int sum = 0;
for(int i=1;i<n;i*=2)for (int j=0;j<i;j++)sum++;
A.O(logn) B.O(n) C.O(nlogn) D.O( n 2 n^2 n2)
i = 1,2,4,8,…, 2 k − 1 2^{k-1} 2k−1( 2 k − 1 2^{k-1} 2k−1<n)
T = 1+2+4+8+…+ 2 k − 1 2^{k-1} 2k−1= 2 k 2^k 2k-1
n<T<2n,时间复杂度为O(n)
6 时间复杂度计算方法(一、二、三层循环)



相关文章:

数据结构练习题1:基本概念
练习题1:基本概念 1 抽象数据类型概念分析2. 逻辑结构与存储结构概念分析3.综合选择题4.综合判断题5.时间复杂度相关习题6 时间复杂度计算方法(一、二、三层循环) 1 抽象数据类型概念分析 1.可以用(抽象数据类型)定义…...

如何消除Msxml2.XMLHTTP组件的缓存
之前使用这个组件,是每隔十分钟取数据,没有遇到这个缓存问题, 这次使用它是频繁访问接口,就出现了一直不变的问题。觉得是缓存没有清除的问题。 网上搜了一些方案。最好的方案就是给url地址末尾给一个随机参数。用于让组件觉得是…...
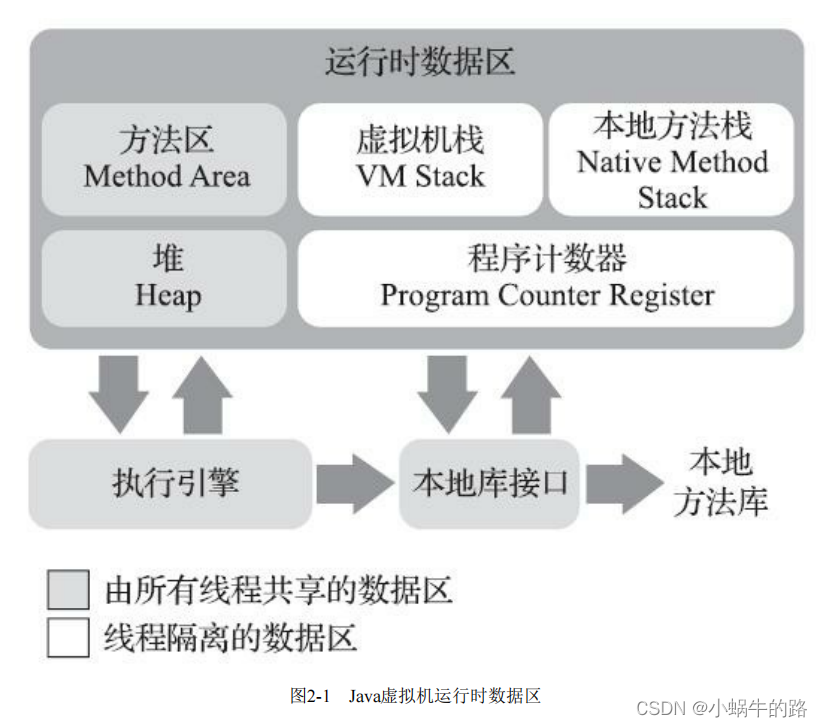
深入理解Java虚拟机jvm-运行时数据区域(基于OpenJDK12)
运行时数据区域 运行时数据区域程序计数器Java虚拟机栈本地方法栈Java堆方法区运行时常量池直接内存 运行时数据区域 Java虚拟机在执行Java程序的过程中会把它所管理的内存划分为若干个不同的数据区域。这些区域有各自的用途,以及创建和销毁的时间,有的…...
 基础demo)
(OpenCV) 基础demo
文章目录 前言Demo图片录制播放人脸识别 END 前言 OpenCV - Open Computer Vision Library OpenCV的名声想必不用多说了。 本文介绍4个基础使用demo。分别为,显示图片,录制视频,播放视频和一个基于开源算法库的人脸识别小demo。 只要环境…...

using 的使用
作者: 苏丙榅 链接: https://subingwen.cn/cpp/using/ 在 C 中 using 用于声明命名空间,使用命名空间也可以防止命名冲突。在程序中声明了命名空间之后,就可以直接使用命名空间中的定义的类了。在 C11 中赋予了 using 新的功能,让C变得更年轻…...

Websocket、Socket、HTTP之间的关系
Websocket、Socket、HTTP之间的关系 ★ Websocket是什么?★ Websocket的原理★ websocket具有以下特点:★ webSocket可以用来做什么?★ websocket与socket区别:★ WebSocket与HTTP区别 ★ Websocket是什么? ● Websocket是HTML5下…...

hustoj LiveCD版系统在局域网虚拟机安装和配置
root权限 打开terminal命令行输入sudo su输入初始密码freeproblemsetmysql数据库的密码的位置,如何登陆数据库 数据库账号密码存放在两个配置文件中: /home/judge/etc/judge.conf/home/judge/src/web/include/db_info.inc.php 新版本中,快…...

读书-代码整洁之道10-14
类 类的三大特性:封装、继承、多态;类应该短小;单一权责原则认为,类或模块应有且只有一条加以修改的理由;当类丧失了内聚性,就拆分它;隔离修改 系统 构造和使用是非常不一样的过程。每个应用…...

UDP 广播/组播
广播UDP与单播UDP的区别就是IP地址不同,广播使用广播地址xxx.xxx.xxx.255,将消息发送到在同一广播网络上的每个主机,广播/组播只能用udp进行实现 函数:int setsockopt(int sockfd, int level, int optname, const void *optval, socklen_topt…...

高效创作助手:ChatGPT最新版实现批量撰写聚合文章的全新水平
随着人工智能技术的不断发展,ChatGPT最新版作为一款智能创作助手,实现了批量撰写聚合文章的全新水平。它能够在短时间内生成高质量的文章,极大地提高了创作效率。本文将从随机8-20个方面对ChatGPT最新版进行详细的阐述,让我们一起…...

Python中的包是什么,如何创建和使用包?
在Python中,包是一种将相关模块分组在一起的方式。它可以让我们更好地组织和重用代码。 一个Python包实际上是一个文件夹,其中包含该包的Python模块和其他资源文件(例如配置文件、数据文件等)。包的根目录通常包含一个名为__init…...
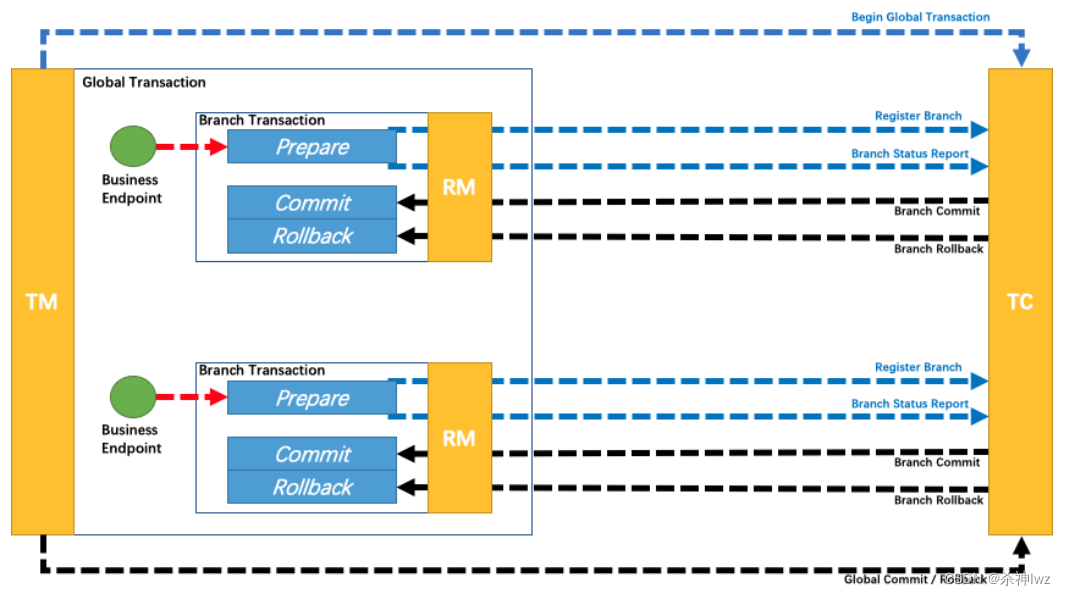
Spring Cloud Alibaba Seata(二)
目录 一、Seata 1、Seata-AT模式 1.1、具体案例 1.2、通过Seata的AT模式解决分布式事务 2、Seata-XA模式 3、Seata-TCC模式 4、Seata-SAGA模式 一、Seata 1、Seata-AT模式 概念:AT模式是一种无侵入的分布式事务解决方案,在 AT 模式下,…...

如何在 MySQL 中使用 COALESCE 函数
1. 简介 在 MySQL 中,COALESCE 函数可以用来返回参数列表中的第一个非空值。如果所有参数都为空,则返回 NULL。本文将介绍 COALESCE 函数的语法和用法,并通过示例演示其效果。 2. 语法 COALESCE 函数的语法如下所示: COALESCE(…...
——初识分布式爬虫scrapy_redis)
Python爬虫之Scrapy框架系列(22)——初识分布式爬虫scrapy_redis
目录: 分布式爬虫(Scrapy\_redis):1.简单介绍:2.Scrapy_redis的安装:分布式爬虫(Scrapy_redis): 官方文档:https://scrapy-redis.readthedocs.io/en/stable/1.简单介绍: scrapy_redis是一个基于Redis的Scrapy组件,用于scrapy项目的分布式部署和开发。 特点: 分布…...
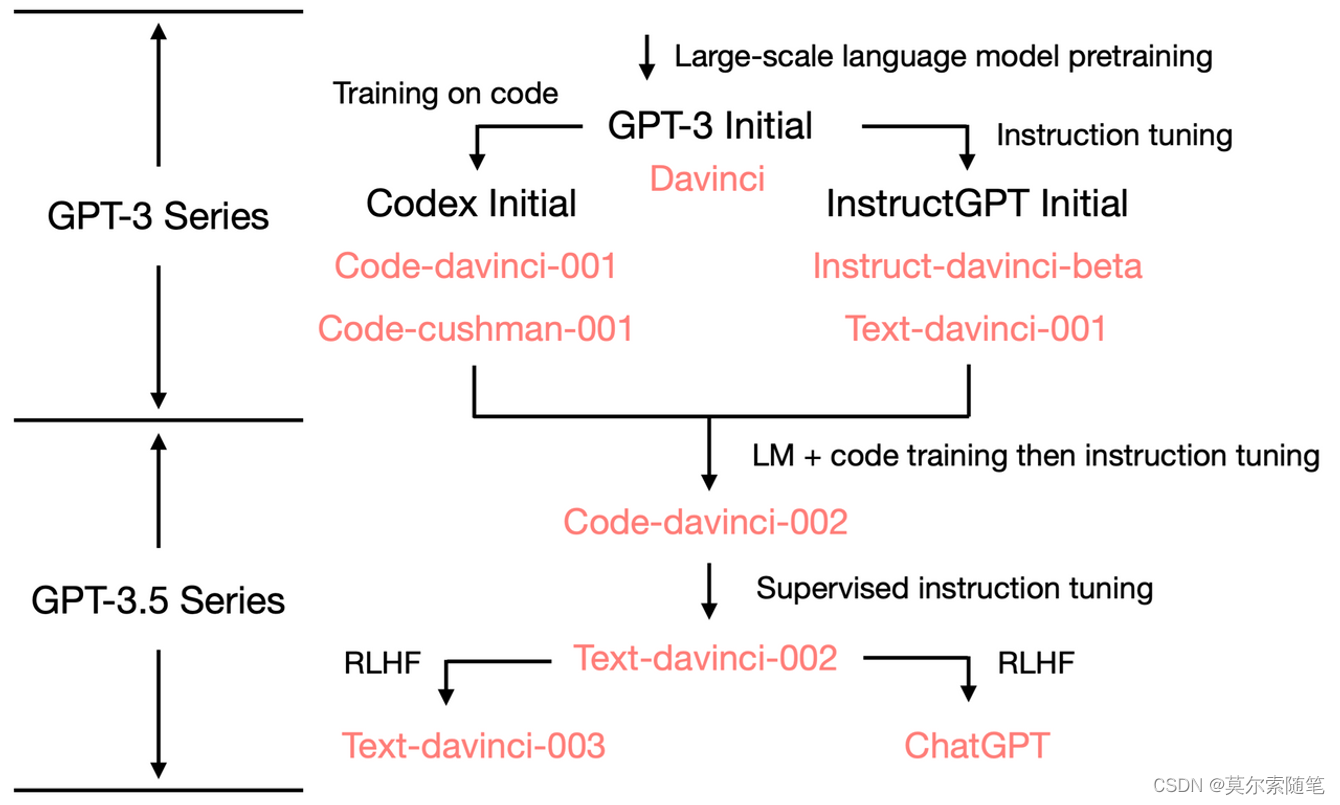
ChatGPT的前世今生
原文首发于博客文章ChatGPT发展概览 ChatGPT 是OpenAI开发的人工智能聊天机器人程序,于2022年11月推出。该程序使用基于 GPT-3.5、GPT-4 架构的大语言模型并以强化学习训练。ChatGPT目前仍以文字方式交互,而除了可以用人类自然对话方式来交互,…...
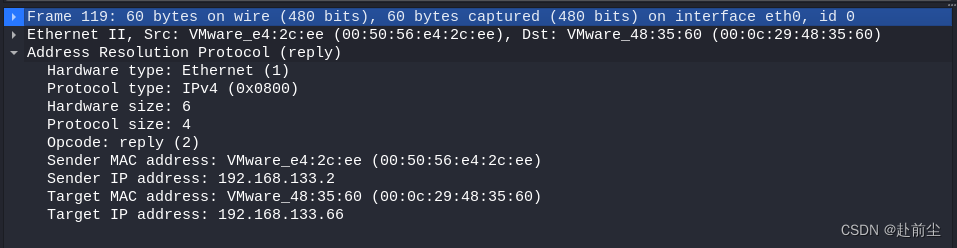
WireShark常用协议抓包与原理分析
1.ARP协议(地址解析协议) nmap 发现网关nmap -sn 192.168.133.2wireshark 抓请求包和响应包 arp请求包内容 arp响应包内容 总结:请求包包含包类型(request),源IP地址,源MAC地址,目标IP地址,目标MAC地址(未知,此处为全0);响应包包含包类型(reply),源IP地址,源…...
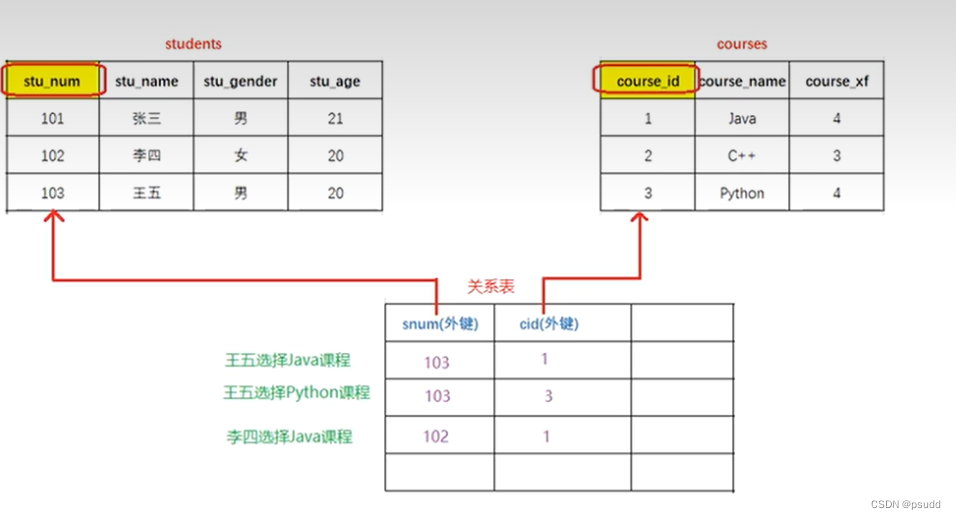
Mysql数据库操作总结
文章目录 1. DDL(Data Definition Language - 数据定义语言)1.1 数据库1.2 数据表(创建查询删除)1.3 数据表(修改) 2. 数据类型2.1 数值2.2 字符2.3 日期 3. 字段约束3.1 约束3.2 主键约束修改3.3 主键自增 联合主键 4. DML(Data Manipulation Language - 数据操作语言)4.1 添…...

在 ZBrush、Substance 3D Painter 和 UE5 中创作警探角色(P2)
大家好,下篇分享咱们继续来说警探角色的重新拓扑、UV、材质贴图和渲染处理。 重新拓扑/UV 这是对我来说最不有趣的部分——重新拓扑。它显然是实时角色中非常重要的一部分,不容忽视,因为它会影响大量的 UV、绑定和后期渲染,这里…...
如何在大规模服务中迁移缓存
当您启动初始服务时,通常会过度设计以考虑大量流量。但是,当您的服务达到爆炸式增长阶段,或者如果您的服务请求和处理大量流量时,您将需要重新考虑您的架构以适应它。糟糕的系统设计导致难以扩展或无法满足处理大量流量的需求&…...
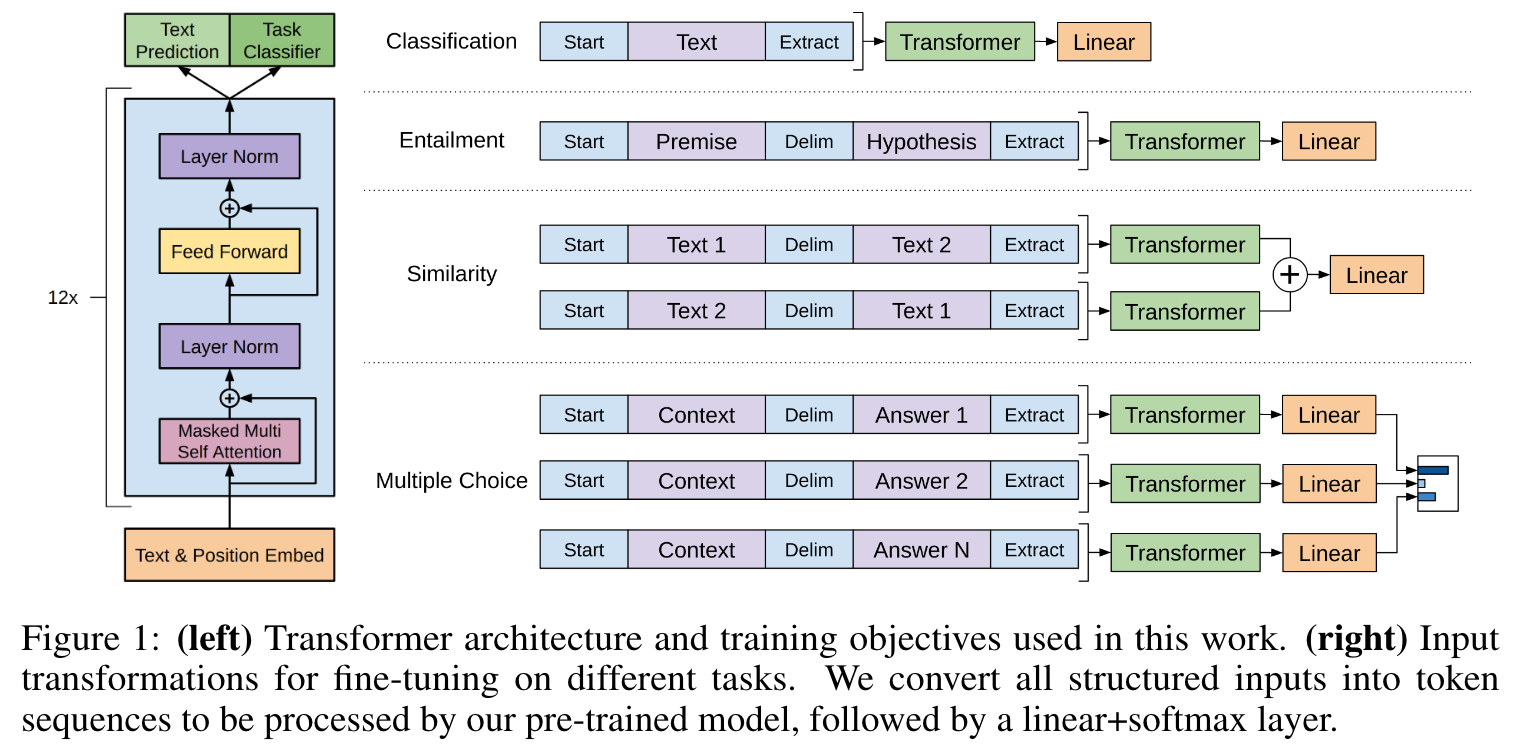
【GPT LLM】跟着论文学习gpt
GPT1开山之作:Improving language understanding by generative pre-training 本文提出了gpt1,即使用无标签的数据对模型先进行训练,让模型学习能够适应各个任务的通用表示;后使用小部分 task-aware的数据对模型进行微调ÿ…...

(十)学生端搭建
本次旨在将之前的已完成的部分功能进行拼装到学生端,同时完善学生端的构建。本次工作主要包括: 1.学生端整体界面布局 2.模拟考场与部分个人画像流程的串联 3.整体学生端逻辑 一、学生端 在主界面可以选择自己的用户角色 选择学生则进入学生登录界面…...

Xshell远程连接Kali(默认 | 私钥)Note版
前言:xshell远程连接,私钥连接和常规默认连接 任务一 开启ssh服务 service ssh status //查看ssh服务状态 service ssh start //开启ssh服务 update-rc.d ssh enable //开启自启动ssh服务 任务二 修改配置文件 vi /etc/ssh/ssh_config //第一…...

DockerHub与私有镜像仓库在容器化中的应用与管理
哈喽,大家好,我是左手python! Docker Hub的应用与管理 Docker Hub的基本概念与使用方法 Docker Hub是Docker官方提供的一个公共镜像仓库,用户可以在其中找到各种操作系统、软件和应用的镜像。开发者可以通过Docker Hub轻松获取所…...

安宝特方案丨XRSOP人员作业标准化管理平台:AR智慧点检验收套件
在选煤厂、化工厂、钢铁厂等过程生产型企业,其生产设备的运行效率和非计划停机对工业制造效益有较大影响。 随着企业自动化和智能化建设的推进,需提前预防假检、错检、漏检,推动智慧生产运维系统数据的流动和现场赋能应用。同时,…...

Mybatis逆向工程,动态创建实体类、条件扩展类、Mapper接口、Mapper.xml映射文件
今天呢,博主的学习进度也是步入了Java Mybatis 框架,目前正在逐步杨帆旗航。 那么接下来就给大家出一期有关 Mybatis 逆向工程的教学,希望能对大家有所帮助,也特别欢迎大家指点不足之处,小生很乐意接受正确的建议&…...
【机器视觉】单目测距——运动结构恢复
ps:图是随便找的,为了凑个封面 前言 在前面对光流法进行进一步改进,希望将2D光流推广至3D场景流时,发现2D转3D过程中存在尺度歧义问题,需要补全摄像头拍摄图像中缺失的深度信息,否则解空间不收敛…...

Springcloud:Eureka 高可用集群搭建实战(服务注册与发现的底层原理与避坑指南)
引言:为什么 Eureka 依然是存量系统的核心? 尽管 Nacos 等新注册中心崛起,但金融、电力等保守行业仍有大量系统运行在 Eureka 上。理解其高可用设计与自我保护机制,是保障分布式系统稳定的必修课。本文将手把手带你搭建生产级 Eur…...

网络编程(UDP编程)
思维导图 UDP基础编程(单播) 1.流程图 服务器:短信的接收方 创建套接字 (socket)-----------------------------------------》有手机指定网络信息-----------------------------------------------》有号码绑定套接字 (bind)--------------…...

Python ROS2【机器人中间件框架】 简介
销量过万TEEIS德国护膝夏天用薄款 优惠券冠生园 百花蜂蜜428g 挤压瓶纯蜂蜜巨奇严选 鞋子除臭剂360ml 多芬身体磨砂膏280g健70%-75%酒精消毒棉片湿巾1418cm 80片/袋3袋大包清洁食品用消毒 优惠券AIMORNY52朵红玫瑰永生香皂花同城配送非鲜花七夕情人节生日礼物送女友 热卖妙洁棉…...

【C++特殊工具与技术】优化内存分配(一):C++中的内存分配
目录 一、C 内存的基本概念 1.1 内存的物理与逻辑结构 1.2 C 程序的内存区域划分 二、栈内存分配 2.1 栈内存的特点 2.2 栈内存分配示例 三、堆内存分配 3.1 new和delete操作符 4.2 内存泄漏与悬空指针问题 4.3 new和delete的重载 四、智能指针…...
