审批流、工作流、业务流
是业务流、工作流、审批流
业务流:即业务流程,指为了完成某项业务而进行的各种工作的有序组合
工作流:即工作流程,指为了完成某项工作而进行的各种动作的有序组合
审批流:即审批流程,是对某项工作的审批活动的有序组合
工作流详解
一项完整的工作流程,应包括流程定义、权限划分两个部分,见如下泳道图:
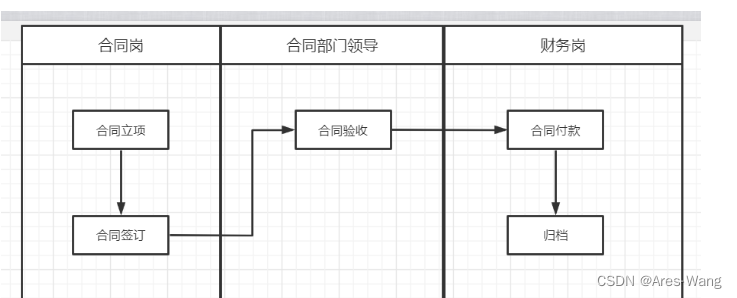
合同签订的流程从开始到结束,共需要经过5个环节,涉及三个岗位。
- 流程定义
流程定义的目的,是为了将工作分解并确定分解后的事项先后顺序。
1)工作流程
一个工作流具体包含哪些流程环节以及各环节之间的先后顺序。
比如上图的合同工作流程,包含合同立项-合同签订-合同验收-合同付款-归档五个环节。
合同立项的后置环节是合同签订,以此类推。
在具体开发时,各环节及顺序可以系统内写死也可以自由配置,具体视业务变动频率及开发资源确定。
2)表单设计
即本环节内,应该确定、处理什么内容。
比如合同立项环节,业务人员需要确定并填写合同的甲乙方、立项时间、立项金额等内容。
那么立项表单设计时,就要包含上述的字段信息。
简单的工作流:各环节之间无分支条件,无流程跨越
复杂的工作流:要考虑各环节之间的分支条件,比如满足条件A,走流程1,否则走流程2等,还有环节间的退回情况等
2. 权限的划分
权限划分的目的,是为了确定事项责任归属,即由谁做什么操作。
权限包含功能权限、数据权限、字段权限。
1)功能权限
即用户能看到哪些菜单,能进行什么操作(按钮)。
比如同是合同岗,员工A只有立项权限,无合同签订权限,员工B只有签订权限无立项权限。
2)数据权限
即用户能查看或操作的数据范围,只能查看或操作授权内的数据。
比如员工A只能查看本部门的合同,员工B可以查看全公司的合同。
3)字段权限
即用户能查看或操作的数据字段,只能查看或操作授权内的字段。
比如员工A不可查看合同的立项金额字段,员工B可以查看合同所有字段。
具体权限的设计,需要根据各业务特性及需求来确定。
权限设计参考RBAC权限模型,本文不再赘述。
四、审批流详解
审批流是属于工作流的一个组成部分,所以审批流的设计与工作流基本相似。
还是以合同流程讲解,如下流程:
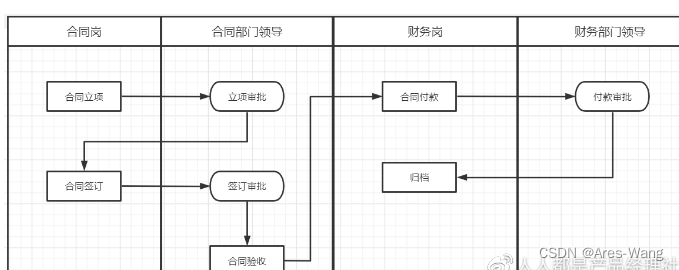
假设合同立项、合同签订、合同付款均需审批,审批通过后才可进入下一环节。
每个环节的审批人可以是多人,也可以是单人,可以是多人串行审批,也可以是多人并行审批等等。
- 审批流的触发条件
1)必须审批
指不管当前操作人的权限,环节提交后均需审批。
比如合同立项,提交后必须立项审批。
2)权限外审批
根据当前操作人的权限,若在其权限内,则无需审批并直接进入下一个环节,否则需审批。
比如合同立项,如果立项人员的立项权限是20万,合同立项金额低于20万则直接进入合同签订环节,否则进入立项审批环节。

2. 审批流的设置
关于审批流设置的文章比较多,本文不再赘述。
工作流最重要的点就是理清流程、确定权限,把好这两个要点,工作流设计便不是问题了。
相关文章:

审批流、工作流、业务流
是业务流、工作流、审批流 业务流:即业务流程,指为了完成某项业务而进行的各种工作的有序组合 工作流:即工作流程,指为了完成某项工作而进行的各种动作的有序组合 审批流:即审批流程,是对某项工作的审批活动…...
如何利用知识库加强内部管理?
许多公司都知道需要有一个面向客户的知识库,以加强客户服务,提供更好的客户体验。 但是很多企业没有意识到的是,拥有一个内部知识库软件对于员工改善沟通和促进知识共享的重要性。 协作是组织成功的关键部分,通过明确的远景和使…...

饕餮 NFT 作品集来袭!
饕餮 NFT 作品集包含 Chili Game 创作的体验《饕餮》第一章中的角色。可以在 The Sandbox 农历新年活动期间(01/18/23 至 02/28/23)体验。 饕餮的故事植根于中国古代神话,主要灵感来自《山海经》,一个关于捉妖人「青蛙侠」的故事。…...

C++中的内存分区、引用、函数
内存分区模型 代码区 存放CPU执行的机器指令代码区是共享的且具有只读性 全局区 全局变量和静态变量都存放在此处全局区还包括了常量区、字符串常量和其他常量也存放在此该区域的数据在程序结束后由操作系统释放const修饰的局部变量并不算在全局区 栈区 由编译器自动分配和释放…...

关于angular表格total模板中一直为0
哈喽 小伙伴们大家好昨天在用angular得antdesign组件得table表格 我用total模板 结果,total一直为0这可是愁坏我了 <ng-template #totalTemplate let-total>找到 {{ total }} 条结果</ng-template>[nzShowTotal]"totalTemplate"最后找到原因了…...
多线程事务怎么回滚
背景介绍1,最近有一个大数据量插入的操作入库的业务场景,需要先做一些其他修改操作,然后在执行插入操作,由于插入数据可能会很多,用到多线程去拆分数据并行处理来提高响应时间,如果有一个线程执行失败&…...
设计(五:基于Carry4的高精度TDC设计))
基于FPGA的时间数字转换(TDC)设计(五:基于Carry4的高精度TDC设计)
1.基于Carry4进位链设计原理 常见的基于FPGA开发的TDC有直接计数法,多相位时钟采样法,抽头延迟线法等,之前内容为基于多相位的TDC,本章节中,主要讲解基于抽头延迟线法。在Xilinx FPGA开发中,实现抽头延迟线法有很多种,如使用IODELAY构建延迟进位链,此处将介绍基于Carr…...

【C++】二叉搜索树的实现(递归和非递归实现)
文章目录1、二叉搜索树1.1 构建二叉搜索树1.2 二叉搜索树的插入1.3 二叉搜索树的删除1.4 二叉搜索树插入和删除的递归实现为了学习map和set的底层实现,需要知道红黑树,知道红黑树之前需要知道AVL树。 红黑树和AVL树都用到了二叉搜索树结构,所…...

春招来了,如何正确使用领英超高效招聘海外员工、挖掘人才?
金三银四到了,每年的这个时候都是企业招聘的好时机。而领英是目前全球最大的职场社交网络平台,基本上海外求职都是在使用它,所以很多企业涉及到海外招聘时,都会优先考虑领英,但是却经常缺乏一些经验技巧,今…...

Mysql中锁机制深入理解
Mysql中锁机制深入理解默认大家已经知道。分类性能悲观锁,乐观锁操作类型读锁,写锁,数据粒度表锁,行锁,页面锁更细粒度间隙锁,临键锁按使用来讲。由数据粒度出发。表锁,分为 共享锁,…...

去中心化社交网络协议除了Nostr还有哪些?
当下最火的去中心化社交软件Dmaus就是基于Nostr协议开发的,Nostr协议的基本情况之前的文章《一文了解去中心化社交网络协议Nostr》已经做了详细介绍,本文将介绍其他几个目前比较流行的去中心化社交协议。FarcasterFarcaster是由前Coinbase高管Dan Romero…...

【FT2000/4+X100】调试记录
订阅专栏 硬件环境FT2000/4+X100,单板结构,对外显示,运行银行麒麟操作系统。 一 生成UEFI.BIN,烧写在FT2000-4的QSPI Flash中 1 2 下载源文件 edk2-for-support.tar; 参考文件 ft2004c&D2000编译打包说明V1.0.5; 解压源文件; 根目录下 build2004C.sh为四核产品…...
我的Android启动优化—【黑白屏优化】
简述 在Android App使用过程中,对于应用的优化是一个加分项,举个例子,打开你的App需要2秒,人家0.5秒,这就是很大的用户体验上的优化。 问题的产生 在开发中,我们在启动app的时候,屏幕会出现一…...

TongWeb8编码设置说明
应用场景:在遇到中文问题时,常需要通过设置编码格式来解决问题。下面介绍TongWeb8的编码设置及优先级。一、web.xml中请求、响应编码的配置优先级最高在JavaEE8规范中web.xml增加了request, response编码配置,该配置优先级最高。<?xml ve…...

不同相机之间图片像素对应关系求解(单应性矩阵求解)
一、场景 相机1和相机2相对位置不变,相机拍摄图片有重叠,求他们交叠部分的一一对应关系。数学语言描述为已知相机1图片中P点像素(u1, v1),相机1中P点在相机2图片中像素值为(u2, v2),它们存在某种变换,求变换矩阵。 因为…...

远程管理时代,还得是智能化PDU才靠得住!
在如今这个信息技术高速发展的时代,数据中心IDC机房服务器数量与日俱增,提供DNS域名服务、主机托管服务、虚拟主机服务等服务的服务器是IDC最基本的功能之一。服务器需要7*24小时不间断持续工作,但当服务器数量很大,服务器工作、重…...
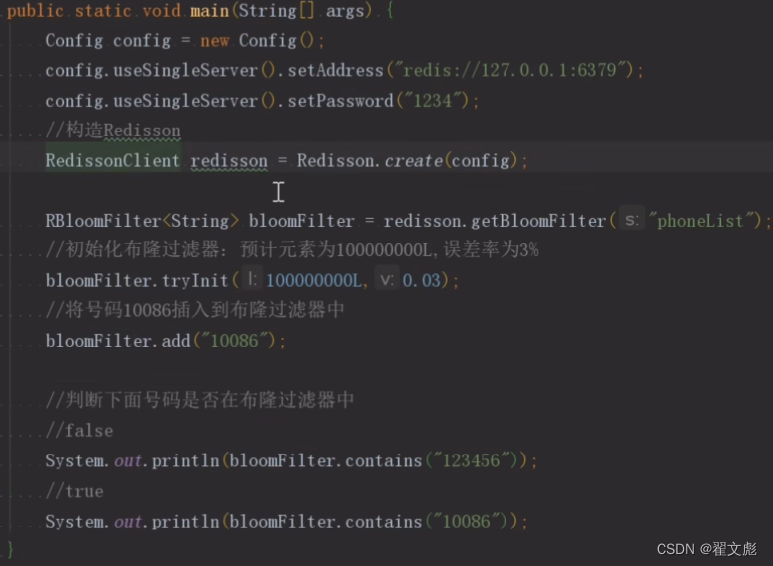
通俗易懂理解——布隆过滤器
文章目录概述本质优缺点优点:缺点:实际应用解决redis缓存穿透问题:概述 本质 本质:很长的二进制向量(数组) 主要作用:判断一个数据在这个数组中是否存在,如果不存在为0,…...

TypeScript 学习之类型推导
在一些情况下,代码上没有显性明确类型,typescript 可以隐形推断出类型。 基础 let x 3;变量x的类型被推断为数字。 类型推断发生在初始化变量和成员,设置默认参数值和决定函数返回值时 最佳通用类型 let x [0, 1, null]; // 类型为 numb…...

Android四大组件——Service详解
Service 为后台运行,不可见,没有界面。优先级高于Activity(内存不足时先杀掉Activity),运行在主线程且不能做耗时操作。 一、Service 启动方式 1、startService() 通过 startService 启动后,service会一直…...

svg转png
svg转png写了一个spring boot项目,支持传入svg文件转出png图片,并且自定义转出png的宽和高。主要代码如下:所需依赖如下:演示如下:首先,运行项目使用接口调用工具调用接口发送请求,提取文件1000…...

Flask RESTful 示例
目录 1. 环境准备2. 安装依赖3. 修改main.py4. 运行应用5. API使用示例获取所有任务获取单个任务创建新任务更新任务删除任务 中文乱码问题: 下面创建一个简单的Flask RESTful API示例。首先,我们需要创建环境,安装必要的依赖,然后…...

以下是对华为 HarmonyOS NETX 5属性动画(ArkTS)文档的结构化整理,通过层级标题、表格和代码块提升可读性:
一、属性动画概述NETX 作用:实现组件通用属性的渐变过渡效果,提升用户体验。支持属性:width、height、backgroundColor、opacity、scale、rotate、translate等。注意事项: 布局类属性(如宽高)变化时&#…...

YSYX学习记录(八)
C语言,练习0: 先创建一个文件夹,我用的是物理机: 安装build-essential 练习1: 我注释掉了 #include <stdio.h> 出现下面错误 在你的文本编辑器中打开ex1文件,随机修改或删除一部分,之后…...

React19源码系列之 事件插件系统
事件类别 事件类型 定义 文档 Event Event 接口表示在 EventTarget 上出现的事件。 Event - Web API | MDN UIEvent UIEvent 接口表示简单的用户界面事件。 UIEvent - Web API | MDN KeyboardEvent KeyboardEvent 对象描述了用户与键盘的交互。 KeyboardEvent - Web…...

2025盘古石杯决赛【手机取证】
前言 第三届盘古石杯国际电子数据取证大赛决赛 最后一题没有解出来,实在找不到,希望有大佬教一下我。 还有就会议时间,我感觉不是图片时间,因为在电脑看到是其他时间用老会议系统开的会。 手机取证 1、分析鸿蒙手机检材&#x…...

今日科技热点速览
🔥 今日科技热点速览 🎮 任天堂Switch 2 正式发售 任天堂新一代游戏主机 Switch 2 今日正式上线发售,主打更强图形性能与沉浸式体验,支持多模态交互,受到全球玩家热捧 。 🤖 人工智能持续突破 DeepSeek-R1&…...
 自用)
css3笔记 (1) 自用
outline: none 用于移除元素获得焦点时默认的轮廓线 broder:0 用于移除边框 font-size:0 用于设置字体不显示 list-style: none 消除<li> 标签默认样式 margin: xx auto 版心居中 width:100% 通栏 vertical-align 作用于行内元素 / 表格单元格ÿ…...

Device Mapper 机制
Device Mapper 机制详解 Device Mapper(简称 DM)是 Linux 内核中的一套通用块设备映射框架,为 LVM、加密磁盘、RAID 等提供底层支持。本文将详细介绍 Device Mapper 的原理、实现、内核配置、常用工具、操作测试流程,并配以详细的…...

Kafka主题运维全指南:从基础配置到故障处理
#作者:张桐瑞 文章目录 主题日常管理1. 修改主题分区。2. 修改主题级别参数。3. 变更副本数。4. 修改主题限速。5.主题分区迁移。6. 常见主题错误处理常见错误1:主题删除失败。常见错误2:__consumer_offsets占用太多的磁盘。 主题日常管理 …...

Elastic 获得 AWS 教育 ISV 合作伙伴资质,进一步增强教育解决方案产品组合
作者:来自 Elastic Udayasimha Theepireddy (Uday), Brian Bergholm, Marianna Jonsdottir 通过搜索 AI 和云创新推动教育领域的数字化转型。 我们非常高兴地宣布,Elastic 已获得 AWS 教育 ISV 合作伙伴资质。这一重要认证表明,Elastic 作为 …...
