【面试之闭包】前端面试那些事(2)三分钟深入理解闭包(附详解实例)
目录
- 1、什么是闭包,什么是作用域
- 1.1 变量作用域
- 1.2 闭包是啥?如何改变变量调用格局
- 1.3 闭包的特性
- 2、怎么用闭包,闭包实例应用
- 2.1 常见闭包实例
- 2.2 闭包异步函数的应用
- 2.3 柯里化的应用
- 3、闭包的优缺点
- 3.1 优点
- 3.2 缺点
- 4、片尾彩蛋
【写在前面】2023年确实想整理好一些前端的学习心得,另外也秉着不让后学习者少走弯路的原则,博主是日夜挑灯阅尽千篇才整理出来的,闭包一直是面试高频词汇,也是很多高级应用必不可缺的,下面务必给我三分钟,让我为您详细解答一下闭包的前世今生。希望能给您带来帮助。
涉及知识点:变量作用域;闭包;垃圾回收机制,;立即执行函数;闭包异步函数,柯里化
1、什么是闭包,什么是作用域
1.1 变量作用域
闭包理解的前提是我们应该先去理解变量作用域,正常也无外乎全局变量和局部变量;
全局变量能被所有的函数应用,局部变量的话只能在声明区域应用。
好比如下所示的函数:
var hdd = '黄大大';
function hddFunc(){
var kf = '黄小小';console.log(hdd+'好帅');
}
function kongfu(){console.log(kf+'好丑');
}
hddFunc(); //输出黄大大好帅
kongfu(); //输出报错,VM138:7 Uncaught ReferenceError kf is not defined
从上面的实例我们不难发现,全局变量谁都能动,局部变量只能在自己地盘使用。
1.2 闭包是啥?如何改变变量调用格局
要是我函数体内就要用外部的变量呢?也不是不可以,接下来看下面这个实例
var hdd = '黄大大';
function hddFunc(){
var kf = '黄小小';console.log(hdd+'好帅');
function kongfu(){console.log(kf+'好丑');
}
}
hddFunc(); //输出黄大大好帅
kongfu(); //输出报错,VM138:7 Uncaught ReferenceError kf is not defined
输出结果还是一样的。那么我将kongfu()调用放在hddFunc()体内呢?如下所示调整:
var hdd = '黄大大';
function hddFunc(){
var kf = '黄小小';console.log(hdd+'好帅');
function kongfu(){console.log(kf+'好丑');
}
kongfu();
}
hddFunc();
//输出黄大大好帅
//输出黄小小好丑
从这个实例不难发现只有在变量声明区内调用才有效,也确实是实现了kongfu()函数输出了非自身区域内变量的值。其实到这里我就讲完了闭包。
总之一句话:
闭包就是指内部函数有权访问到外层函数的作用域,能读取到外层函数作用域声明的变量,或者我们可以将变量kf和函数kongfu()之间的环境(桥梁)叫做闭包,特别要注意的是必须得在父函数内调用。
1.3 闭包的特性
从上面我们可以特别清楚的看的出来,首先是函数内声明函数,其次是函数内部调用外部参数,再者就是回收机制。
其实在上面的函数调用过程中hddFunc函数体内声明的变量kf因为有kongfu()函数的使用,所以永远不会销毁,正常函数体内的局部变量会随着函数执行完成后而销毁。因此在这里我总结一下闭包三大特性:
- 函数嵌套函数;
- 函数内部可调用外层函数声明的变量和参数;
- 闭包机制下的参数和变量是不会被垃圾回收机制回收(销毁);
2、怎么用闭包,闭包实例应用
2.1 常见闭包实例
function hdd() {var sq = 1 function haoshuai() { return ++sq}return haoshuai
}
var hddhs = hdd();
console.log(hddhs());
//输出 2
function hdd() {var sq = 1 function haoshuai() { return ++sq}return haoshuai
}
var hddhs = hdd();
hddhs();
console.log(hddhs());
//输出3
小记:从这里不难发现帅气值变量sq始终都是在的,调用一次就会存储一次加一,从这里就可以确定sq这个变量一直没有被回收。
2.2 闭包异步函数的应用
先用实例和大家介绍一下:
for (var i = 1; i < 5; i++) {setTimeout(function () {console.log(i+"-黄大大好帅");}, 50);
}
//输出:
5-黄大大好帅
5-黄大大好帅
5-黄大大好帅
5-黄大大好帅
但是我就是想让他在遍历里面按照正常顺序来输出。这个时候我们可以用到闭包的概念。我们创建了一个立即执行函数,将变量i放在立即执行函数内,其实也就相当于这里的i被setTimeout异步函数给引用了,从而实现i变量叠加后会保存原有的值。也验证了一点特性,函数嵌套函数的说法
for (var i = 1; i < 5; i++) {(function(i){setTimeout(function () {console.log(i+"-黄大大好帅");}, 50);})(i)
}
//输出:
1-黄大大好帅
2-黄大大好帅
3-黄大大好帅
4-黄大大好帅
其实最推崇的应该是下面这个方式,将变量i用let进行声明,因为let所声明的变量只在let命令所在的代码块内有效。如下所示:
for (let i = 1; i < 5; i++) { setTimeout(function () {console.log(i+"、黄大大好帅");}, 50);
}
//输出:
1-黄大大好帅
2-黄大大好帅
3-黄大大好帅
4-黄大大好帅
2.3 柯里化的应用
柯里化是函数的一种高阶技术,我们可以理解为函数的一种转换,如下:
//求和函数
function sum(a, b,c) { return a + b+c; }
//柯里化辅助函数curry()
//curry函数的实现(不知道多少入参,所以用了递归)
function curry(fn,arr=[]){let len = fn.length; //函数的长度是函数形参的个数return function (...args){let arrs = [...arr,...args];if(arrs.length < len){return curry.call(this,fn,arrs);}else{return fn(...arrs);}}}
let getSum = curry(sum);
console.log(getSum(1,2,3)) //輸出6
console.log(getSum(1)(2,3)) //輸出6
console.log(getSum(1)(2)(3)) //輸出6
我们不难发现里面函数嵌套函数,且应用函数体外的变量。
3、闭包的优缺点
3.1 优点
1.能读取函数外层的变量,从而避免全局变量被污染
2.外层变量会一直存在内存中,函数结束后不会被回收机制回收
3.2 缺点
1.正因为不被回收机制,所以会导致内存消耗过大,伸直引发溢出,所以慎用哦!
4、片尾彩蛋
如果觉得这篇文章对您有帮助的话,想支持博主的可以上皇榜看看哟,皇榜点击此处进入
相关文章:
三分钟深入理解闭包(附详解实例))
【面试之闭包】前端面试那些事(2)三分钟深入理解闭包(附详解实例)
目录1、什么是闭包,什么是作用域1.1 变量作用域1.2 闭包是啥?如何改变变量调用格局1.3 闭包的特性2、怎么用闭包,闭包实例应用2.1 常见闭包实例2.2 闭包异步函数的应用2.3 柯里化的应用3、闭包的优缺点3.1 优点3.2 缺点4、片尾彩蛋【写在前面…...

深入浅出带你学习WebSphere中间件漏洞
前言 上一篇文章给大家介绍了中间件glassfish的一些常见漏洞以及利用方法,今天我给大家带来的是WebSphere中间件的常见漏洞以及这些漏洞的利用方法,下面我们首先介绍一下WebSphere中间件是什么,然后展开来讲关于该中间件的漏洞。 WebSphere…...

如何一眼分辨是C还是C++
C语言的历史C语言是由贝尔实验室的Dennis Ritchie在20世纪70年代初开发的一种通用程序设计语言。在早期的计算机时代,许多计算机使用不同的汇编语言编写程序,这导致了程序的可移植性和代码的可重用性很低。因此,Dennis Ritchie在开发C语言时试…...
CMake系列:正确使用多配置编译系统
目录 常见错误 问题现象 正确做法 if指令应该什么时候使用 活学活用 把IF指令用于多配置编译系统是很多初学者容易犯下的错误。这篇文章启示性的教你如何正确理解、使用CMake的多配置编译系统。 常见错误 以Debug和Release配置有不同的宏定义为例,如下所示&a…...
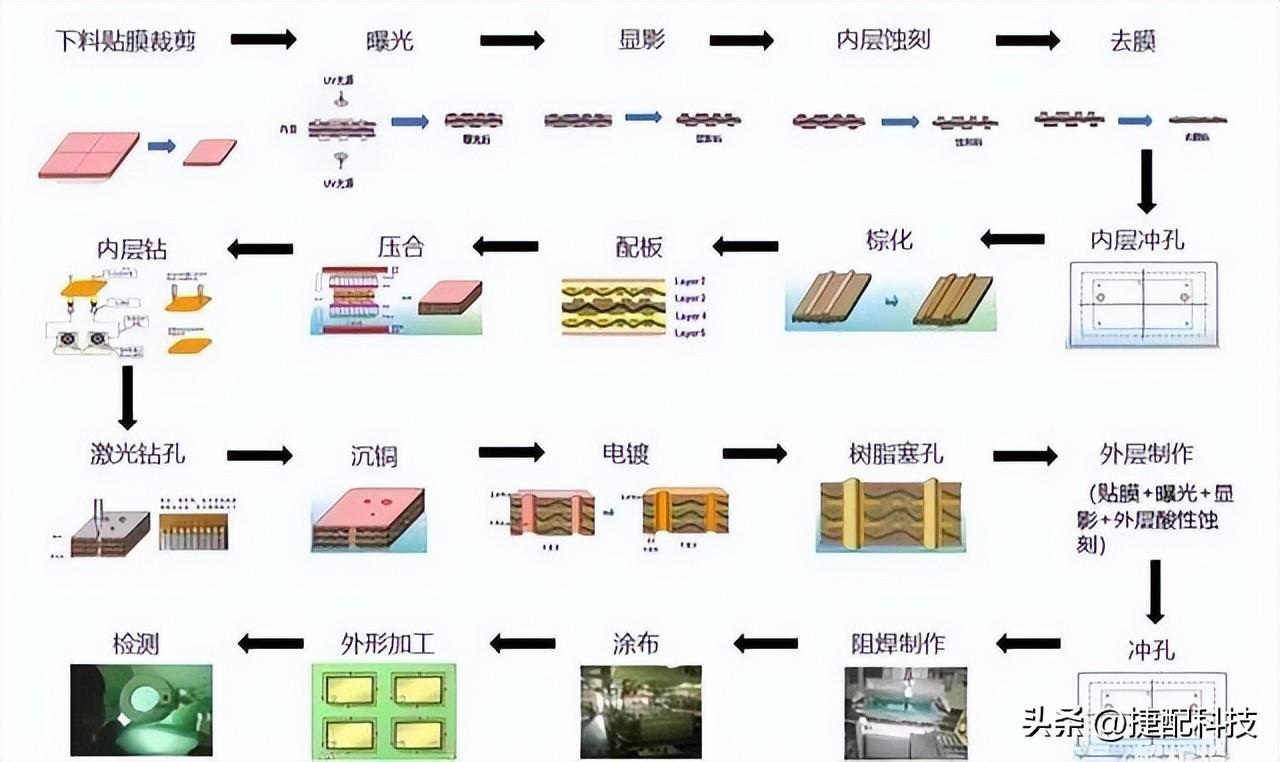
PCB中的HDI板生产中的变化
关键词:HDI概述 HDI发展演变 HDI生产难点如果把一整个电子产业比作浩瀚的宇宙,那些智能电子设备就像宇宙中闪耀的星光,当你以“上帝”的视角手持放大镜去观察时,这些闪烁的星光点点其实都是一个个由精密的“自然规律”所“设计”好…...

程序分析与神经网络后门
原文来自微信公众号“编程语言Lab”:程序分析与神经网络后门 搜索关注“编程语言Lab”公众号(HW-PLLab)获取更多技术内容! 欢迎加入编程语言社区 SIG-程序分析,了解更多程序分析相关的技术内容。 加入方式:…...

redis主从哨兵模式
一.为什么用redis主从模式 1.数据备份:主从复制实现数据的热备份。 2.故障恢复:当主节点出现问题时,由从节点提供服务,实现快速恢复。 3.负载均衡:读写分离,主节点提供写服务,从节点提供读服务。在写少读多时提高Redis的并发。 二.为什么使用哨兵模式 主要用于主节…...
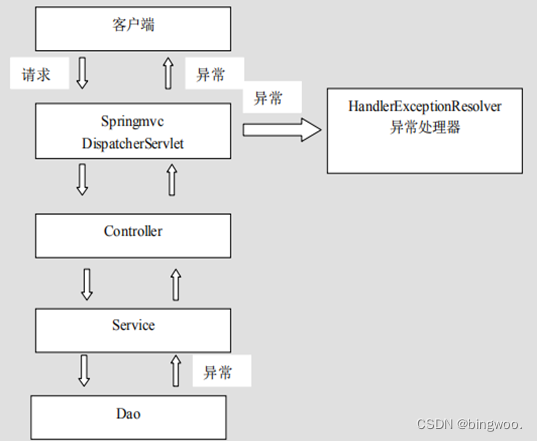
Spring 系列之 MVC
Spring 系列文章目录 文章目录Spring 系列文章目录前言一、介绍二、项目搭建1.创建空项目2.设置maven和lombok3.创建maven web module4. 配置Tomcat启动运行项目(选择local本地)5. 导入jar依赖包6.在web.xml中配置DispatcherServlet7. 加入SpringMVC的配…...
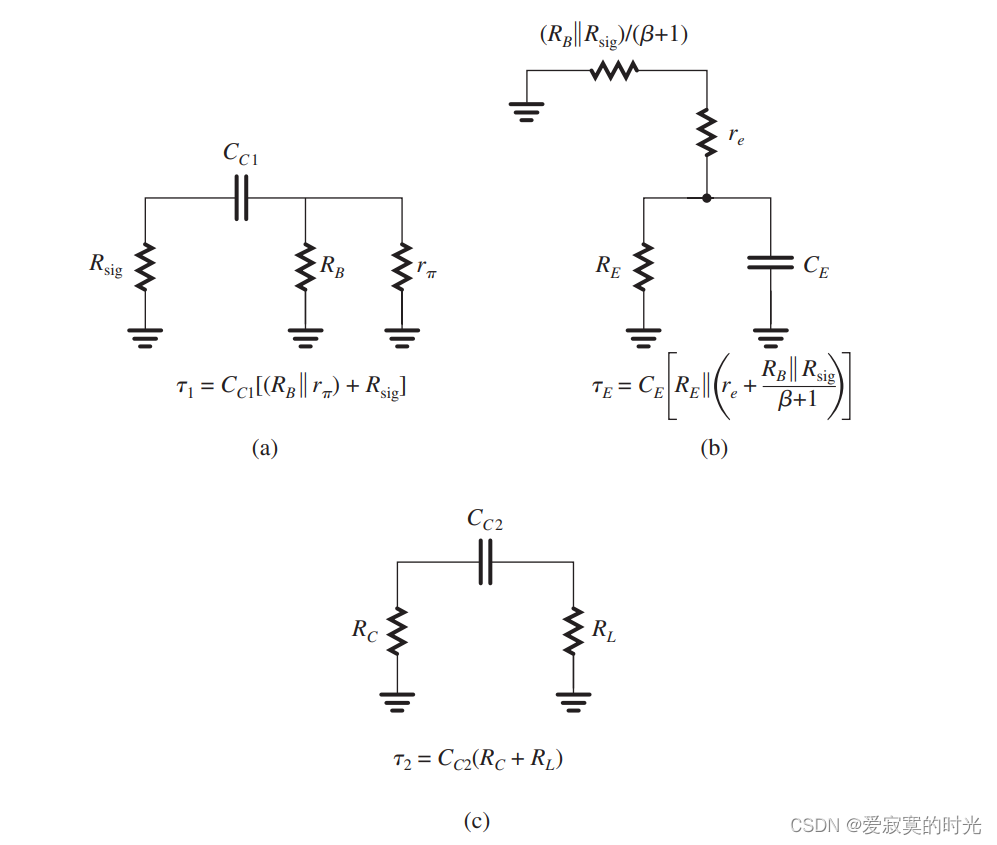
电子技术——分立CS和CE放大器的低频响应
电子技术——分立CS和CE放大器的低频响应 我们之前在学习放大器中从来没有关系过信号频率对放大器的影响,也就是说我们默认放大器具有无限的带宽,这当然不符合现实逻辑。为了说明这一点,我们使用下图: 上图描述了MOS或BJT分立电路…...

代码随想录【Day16】| 104. 二叉树的最大深度、111. 二叉树的最小深度、222. 完全二叉树的节点个数
104. 二叉树的最大深度 题目链接 题目描述: 给定一个二叉树,找出其最大深度。 二叉树的深度为根节点到最远叶子节点的最长路径上的节点数。 说明: 叶子节点是指没有子节点的节点。 示例: 给定二叉树 [3,9,20,null,null,15,7],…...

状态机图、通信图题
1.下列关于通信图与顺序图中的对象的相同点的叙述.正确的是(D)。A.两种图中都可以表示对象的创建和销毁B.对象在两种图中的位置都没有任何限制C.对象在两种图中的表示方式完全一致D.对象名在两种图中的表示完全一致2.下列关于通信图的说法错误的是(C)。A.通信图是对一次交互过程…...

分布式文件存储Minio学习入门
文章目录一、分布式文件系统应用场景1. Minio介绍Minio优点2. MinIO的基础概念、3. 纠删码ES(Erasure Code)4. 存储形式5. 存储方案二、Docker部署单机Minio三、minio纠删码模式部署四、分布式集群部署分布式存储可靠性常用方法冗余校验分布式Minio优势运行分布式minio使用dock…...
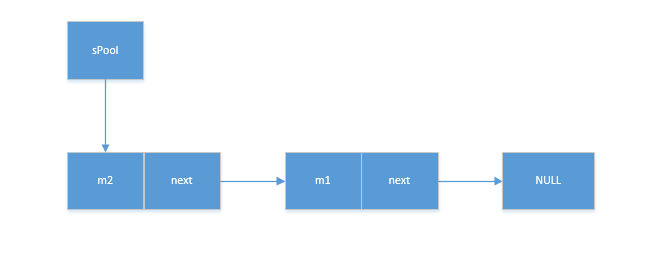
handler解析(4)-Message及Message回收机制
Message中可以携带的信息 Message中可以携带的数据比较丰富,下面对一些常用的数据进行了分析。 /*** 用户定义的消息代码,以便当接受到消息是关于什么的。其中每个Hanler都有自己的命名控件,不用担心会冲突*/ public int what; /*** 如果你…...

Linux使用定时任务监控java进程并拉起
需求描述: 设计一个脚本,通过Linux定时任务,每分钟执行一次,监控jar包进程是否存在,存在则不做动作,不存在则重新拉起jar包程序。 定时任务配置: */1 * * * * bash -x /root/myfile/jars/che…...
Win 10电脑摄像头提示错误代码0xa00f4244怎么办?
如果你的Windows 10电脑无法打开摄像头,提示“我们找不到你的摄像头”的错误消息,错误代码是0xA00F4244,原因可能是杀毒软件阻止了摄像头,或者是摄像头驱动程序有问题。 小编为你整理了摄像头错误代码0xA00F4244的解决方法&#…...
MFC消息机制
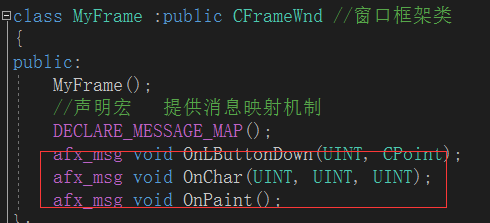
1.消息映射消息映射是一个将消息和成员函数相互关联的表。比如,框架窗口接收到一个鼠标左击消息,MFC将搜索该窗口的消息映射,如果存在一个处理WM_LBUTTTONDOWN消息的处理程序,然后就调用OnButtonDown。2.消息映射机制2.1 声明宏 写…...

全国计算机等级考试报名照片要求以及证件照制作教程
马上就全国计算机等级考试就要开始了,相信现在很多同学都在网上进行报名呢,报名的时候肯定需要用到个人证件照片,所以问题来了,我们怎么自己制作证件照片呢?计算机等级考试报名时对证件照都有哪些要求呢?该…...

SQLSERVER 临时表和表变量到底有什么区别?
一:背景 1. 讲故事 今天和大家聊一套面试中经常被问到的高频题,对,就是 临时表 和 表变量 这俩玩意,如果有朋友在面试中回答的不好,可以尝试看下这篇能不能帮你成功迈过。 二:到底有什么区别 1. 前置思…...

技术生态异军突起,昇思MindSpore进入AI框架第一梯队
ChatGPT掀起的新一轮人工智能狂欢下,隐藏在背后的“大模型”正进入越来越多开发者的视野。 诚如几年前开始流行的一种说法:数据是燃料、模型是引擎、算力是加速器。ChatGPT的出现,恰如其分地诠释了数据、模型和算力的“化学反应”。而在其中…...

审批流、工作流、业务流
是业务流、工作流、审批流 业务流:即业务流程,指为了完成某项业务而进行的各种工作的有序组合 工作流:即工作流程,指为了完成某项工作而进行的各种动作的有序组合 审批流:即审批流程,是对某项工作的审批活动…...
:手搓截屏和帧率控制)
Python|GIF 解析与构建(5):手搓截屏和帧率控制
目录 Python|GIF 解析与构建(5):手搓截屏和帧率控制 一、引言 二、技术实现:手搓截屏模块 2.1 核心原理 2.2 代码解析:ScreenshotData类 2.2.1 截图函数:capture_screen 三、技术实现&…...

华为云AI开发平台ModelArts
华为云ModelArts:重塑AI开发流程的“智能引擎”与“创新加速器”! 在人工智能浪潮席卷全球的2025年,企业拥抱AI的意愿空前高涨,但技术门槛高、流程复杂、资源投入巨大的现实,却让许多创新构想止步于实验室。数据科学家…...

docker详细操作--未完待续
docker介绍 docker官网: Docker:加速容器应用程序开发 harbor官网:Harbor - Harbor 中文 使用docker加速器: Docker镜像极速下载服务 - 毫秒镜像 是什么 Docker 是一种开源的容器化平台,用于将应用程序及其依赖项(如库、运行时环…...

[ICLR 2022]How Much Can CLIP Benefit Vision-and-Language Tasks?
论文网址:pdf 英文是纯手打的!论文原文的summarizing and paraphrasing。可能会出现难以避免的拼写错误和语法错误,若有发现欢迎评论指正!文章偏向于笔记,谨慎食用 目录 1. 心得 2. 论文逐段精读 2.1. Abstract 2…...

Springcloud:Eureka 高可用集群搭建实战(服务注册与发现的底层原理与避坑指南)
引言:为什么 Eureka 依然是存量系统的核心? 尽管 Nacos 等新注册中心崛起,但金融、电力等保守行业仍有大量系统运行在 Eureka 上。理解其高可用设计与自我保护机制,是保障分布式系统稳定的必修课。本文将手把手带你搭建生产级 Eur…...

Vue ③-生命周期 || 脚手架
生命周期 思考:什么时候可以发送初始化渲染请求?(越早越好) 什么时候可以开始操作dom?(至少dom得渲染出来) Vue生命周期: 一个Vue实例从 创建 到 销毁 的整个过程。 生命周期四个…...

FFmpeg avformat_open_input函数分析
函数内部的总体流程如下: avformat_open_input 精简后的代码如下: int avformat_open_input(AVFormatContext **ps, const char *filename,ff_const59 AVInputFormat *fmt, AVDictionary **options) {AVFormatContext *s *ps;int i, ret 0;AVDictio…...

ubuntu22.04 安装docker 和docker-compose
首先你要确保没有docker环境或者使用命令删掉docker sudo apt-get remove docker docker-engine docker.io containerd runc安装docker 更新软件环境 sudo apt update sudo apt upgrade下载docker依赖和GPG 密钥 # 依赖 apt-get install ca-certificates curl gnupg lsb-rel…...

若依登录用户名和密码加密
/*** 获取公钥:前端用来密码加密* return*/GetMapping("/getPublicKey")public RSAUtil.RSAKeyPair getPublicKey() {return RSAUtil.rsaKeyPair();}新建RSAUti.Java package com.ruoyi.common.utils;import org.apache.commons.codec.binary.Base64; im…...

第八部分:阶段项目 6:构建 React 前端应用
现在,是时候将你学到的 React 基础知识付诸实践,构建一个简单的前端应用来模拟与后端 API 的交互了。在这个阶段,你可以先使用模拟数据,或者如果你的后端 API(阶段项目 5)已经搭建好,可以直接连…...
