代码随想录【Day16】| 104. 二叉树的最大深度、111. 二叉树的最小深度、222. 完全二叉树的节点个数
104. 二叉树的最大深度
题目链接
题目描述:
给定一个二叉树,找出其最大深度。
二叉树的深度为根节点到最远叶子节点的最长路径上的节点数。
说明: 叶子节点是指没有子节点的节点。
示例: 给定二叉树 [3,9,20,null,null,15,7],

返回它的最大深度 3 。
难点:
思路:
递归法:递归地遍历左右子树,返回较大的深度值
迭代法:使用层序遍历,结果集中的层数就是二叉树最大的深度~
时间复杂度:O()
空间复杂度:O()
/*** Definition for a binary tree node.* public class TreeNode {* int val;* TreeNode left;* TreeNode right;* TreeNode() {}* TreeNode(int val) { this.val = val; }* TreeNode(int val, TreeNode left, TreeNode right) {* this.val = val;* this.left = left;* this.right = right;* }* }*///递归法
class Solution {public int maxDepth(TreeNode root) {if (root == null) return 0;return Math.max(maxDepth(root.left), maxDepth(root.right))+1;}
}//迭代法——使用层序遍历
class Solution {List<List<Integer>> resList = new ArrayList<>();public int maxDepth(TreeNode root) {if (root == null) return 0;Deque<TreeNode> que = new ArrayDeque<>();que.addLast(root);TreeNode cur;int len;while (!que.isEmpty()) {len = que.size();List<Integer> itemList = new ArrayList<>();for (int i = 0; i < len; i++) {cur = que.pollFirst();itemList.add(cur.val);if (cur.left != null) que.addLast(cur.left);if (cur.right != null) que.addLast(cur.right);}resList.add(itemList);}return resList.size();}
}
- 二叉树节点的深度:指从根节点到该节点的最长简单路径边的条数。
- 二叉树节点的高度:指从该节点到叶子节点的最长简单路径边的条数。

因为求深度可以从上到下去查 所以需要前序遍历(中左右),而高度只能从下到上去查,所以只能后序遍历(左右中)
有的同学一定疑惑,为什么104.二叉树的最大深度 (opens new window)中求的是二叉树的最大深度,也用的是后序遍历。
那是因为代码的逻辑其实是求的根节点的高度,而根节点的高度就是这棵树的最大深度,所以才可以使用后序遍历。
class Solution {
public:int result;void getDepth(TreeNode* node, int depth) {result = depth > result ? depth : result; // 中if (node->left == NULL && node->right == NULL) return ;if (node->left) { // 左getDepth(node->left, depth + 1);}if (node->right) { // 右getDepth(node->right, depth + 1);}return ;}int maxDepth(TreeNode* root) {result = 0;if (root == 0) return result;getDepth(root, 1);return result;}
};
可以看出使用了前序(中左右)的遍历顺序,这才是真正求深度的逻辑!
时长:
5min
收获:
可以一起做了如下两道题目:
- 104.二叉树的最大深度
- 559.n叉树的最大深度
111. 二叉树的最小深度
题目链接
题目描述:
给定一个二叉树,找出其最小深度。
最小深度是从根节点到最近叶子节点的最短路径上的节点数量。
说明: 叶子节点是指没有子节点的节点。
示例:
给定二叉树 [3,9,20,null,null,15,7],

返回它的最小深度 2。
难点:
递归法的单层递归逻辑
思路:
递归法:
特别注意,当左(右)子树为空,不能直接返回左右子树最小深度。

层序遍历:
逐层遍历二叉树,如果出现最小深度的叶子,那么必定是层序遍历所找到的第一个叶子。
时间复杂度:O()
空间复杂度:O()
//递归法
class Solution {public int minDepth(TreeNode root) {if (root == null) return 0;int leftDepth = minDepth(root.left);int rightDepth = minDepth(root.right);if (root.left == null) {return rightDepth+1;}if (root.right == null) {return leftDepth+1;}return Math.min(leftDepth, rightDepth)+1;}
}//层序遍历——优化:结果集可不用维护一个List,仅维护一个int即可
class Solution {List<List<Integer>> resList = new ArrayList<>();public int minDepth(TreeNode root) {if (root == null) return 0;Deque<TreeNode> que = new ArrayDeque<>();que.addLast(root);while(!que.isEmpty()) {int len = que.size();List<Integer> itemList = new ArrayList<>();for (int i = 0; i < len; i++) {TreeNode cur = que.pollFirst();if (cur.left == null && cur.right == null) {return resList.size()+1;}itemList.add(cur.val);if (cur.left != null) que.addLast(cur.left);if (cur.right != null) que.addLast(cur.right);}resList.add(itemList);}return resList.size();}
}
时长:
10min
收获:
强化递归练习
加深了层序遍历的理解
222. 完全二叉树的节点个数
题目链接
题目描述:
给出一个完全二叉树,求出该树的节点个数。
示例 1:
- 输入:root = [1,2,3,4,5,6]
- 输出:6
示例 2:
- 输入:root = []
- 输出:0
示例 3:
- 输入:root = [1]
- 输出:1
提示:
树中节点的数目范围是[0, 5 * 10^4]
0 <= Node.val <= 5 * 10^4
题目数据保证输入的树是 完全二叉树
难点:
层序遍历必能解决,换个思路。
刚开始的思路是想拿左下的结点,一直拿到倒数第二层,这样通过完全二叉树的性质,就可以直接计算出前n-1层的个数,然后遍历最后一层就行,但是问题是:仅仅拿到某一层的首个结点,并不能遍历这一层的所有节点,必须要用队列记录该层的上一层结点。
思路:
针对普通二叉树可以使用:
递归法、层序遍历
针对完全二叉树:
利用完全二叉树的性质
向左拿到leftDepth,向右拿到rightDepth
如果leftDepth、rightDepth一致,说明是满二叉树,直接返回结果
如果不一致,那递归地遍历左右子树(左右子树可能出现满二叉树)
时间复杂度:O(log n × log n)
空间复杂度:O(log n)
class Solution {/*** 针对完全二叉树的解法** 满二叉树的结点数为:2^depth - 1*/public int countNodes(TreeNode root) {if (root == null) return 0;TreeNode left = root.left;TreeNode right = root.right;int leftDepth = 0, rightDepth = 0; // 这里初始为0是有目的的,为了下面求指数方便while (left != null) { // 求左子树深度left = left.left;leftDepth++;}while (right != null) { // 求右子树深度right = right.right;rightDepth++;}if (leftDepth == rightDepth) {return (2 << leftDepth) - 1; // 注意(2<<1) 相当于2^2,所以leftDepth初始为0}return countNodes(root.left) + countNodes(root.right) + 1;}
}
时长:
20min
收获:
很有收获,再消化消化
相关文章:

代码随想录【Day16】| 104. 二叉树的最大深度、111. 二叉树的最小深度、222. 完全二叉树的节点个数
104. 二叉树的最大深度 题目链接 题目描述: 给定一个二叉树,找出其最大深度。 二叉树的深度为根节点到最远叶子节点的最长路径上的节点数。 说明: 叶子节点是指没有子节点的节点。 示例: 给定二叉树 [3,9,20,null,null,15,7],…...

状态机图、通信图题
1.下列关于通信图与顺序图中的对象的相同点的叙述.正确的是(D)。A.两种图中都可以表示对象的创建和销毁B.对象在两种图中的位置都没有任何限制C.对象在两种图中的表示方式完全一致D.对象名在两种图中的表示完全一致2.下列关于通信图的说法错误的是(C)。A.通信图是对一次交互过程…...

分布式文件存储Minio学习入门
文章目录一、分布式文件系统应用场景1. Minio介绍Minio优点2. MinIO的基础概念、3. 纠删码ES(Erasure Code)4. 存储形式5. 存储方案二、Docker部署单机Minio三、minio纠删码模式部署四、分布式集群部署分布式存储可靠性常用方法冗余校验分布式Minio优势运行分布式minio使用dock…...
handler解析(4)-Message及Message回收机制
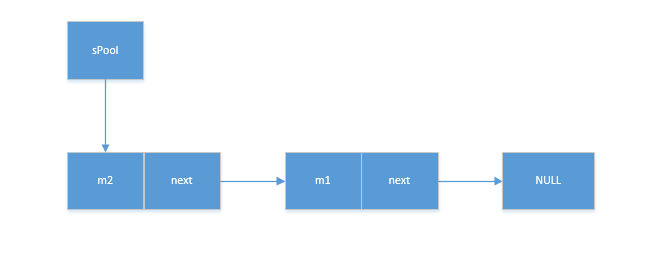
Message中可以携带的信息 Message中可以携带的数据比较丰富,下面对一些常用的数据进行了分析。 /*** 用户定义的消息代码,以便当接受到消息是关于什么的。其中每个Hanler都有自己的命名控件,不用担心会冲突*/ public int what; /*** 如果你…...

Linux使用定时任务监控java进程并拉起
需求描述: 设计一个脚本,通过Linux定时任务,每分钟执行一次,监控jar包进程是否存在,存在则不做动作,不存在则重新拉起jar包程序。 定时任务配置: */1 * * * * bash -x /root/myfile/jars/che…...
Win 10电脑摄像头提示错误代码0xa00f4244怎么办?
如果你的Windows 10电脑无法打开摄像头,提示“我们找不到你的摄像头”的错误消息,错误代码是0xA00F4244,原因可能是杀毒软件阻止了摄像头,或者是摄像头驱动程序有问题。 小编为你整理了摄像头错误代码0xA00F4244的解决方法&#…...
MFC消息机制
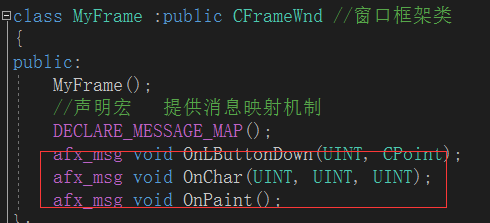
1.消息映射消息映射是一个将消息和成员函数相互关联的表。比如,框架窗口接收到一个鼠标左击消息,MFC将搜索该窗口的消息映射,如果存在一个处理WM_LBUTTTONDOWN消息的处理程序,然后就调用OnButtonDown。2.消息映射机制2.1 声明宏 写…...

全国计算机等级考试报名照片要求以及证件照制作教程
马上就全国计算机等级考试就要开始了,相信现在很多同学都在网上进行报名呢,报名的时候肯定需要用到个人证件照片,所以问题来了,我们怎么自己制作证件照片呢?计算机等级考试报名时对证件照都有哪些要求呢?该…...

SQLSERVER 临时表和表变量到底有什么区别?
一:背景 1. 讲故事 今天和大家聊一套面试中经常被问到的高频题,对,就是 临时表 和 表变量 这俩玩意,如果有朋友在面试中回答的不好,可以尝试看下这篇能不能帮你成功迈过。 二:到底有什么区别 1. 前置思…...

技术生态异军突起,昇思MindSpore进入AI框架第一梯队
ChatGPT掀起的新一轮人工智能狂欢下,隐藏在背后的“大模型”正进入越来越多开发者的视野。 诚如几年前开始流行的一种说法:数据是燃料、模型是引擎、算力是加速器。ChatGPT的出现,恰如其分地诠释了数据、模型和算力的“化学反应”。而在其中…...

审批流、工作流、业务流
是业务流、工作流、审批流 业务流:即业务流程,指为了完成某项业务而进行的各种工作的有序组合 工作流:即工作流程,指为了完成某项工作而进行的各种动作的有序组合 审批流:即审批流程,是对某项工作的审批活动…...
如何利用知识库加强内部管理?
许多公司都知道需要有一个面向客户的知识库,以加强客户服务,提供更好的客户体验。 但是很多企业没有意识到的是,拥有一个内部知识库软件对于员工改善沟通和促进知识共享的重要性。 协作是组织成功的关键部分,通过明确的远景和使…...

饕餮 NFT 作品集来袭!
饕餮 NFT 作品集包含 Chili Game 创作的体验《饕餮》第一章中的角色。可以在 The Sandbox 农历新年活动期间(01/18/23 至 02/28/23)体验。 饕餮的故事植根于中国古代神话,主要灵感来自《山海经》,一个关于捉妖人「青蛙侠」的故事。…...

C++中的内存分区、引用、函数
内存分区模型 代码区 存放CPU执行的机器指令代码区是共享的且具有只读性 全局区 全局变量和静态变量都存放在此处全局区还包括了常量区、字符串常量和其他常量也存放在此该区域的数据在程序结束后由操作系统释放const修饰的局部变量并不算在全局区 栈区 由编译器自动分配和释放…...

关于angular表格total模板中一直为0
哈喽 小伙伴们大家好昨天在用angular得antdesign组件得table表格 我用total模板 结果,total一直为0这可是愁坏我了 <ng-template #totalTemplate let-total>找到 {{ total }} 条结果</ng-template>[nzShowTotal]"totalTemplate"最后找到原因了…...
多线程事务怎么回滚
背景介绍1,最近有一个大数据量插入的操作入库的业务场景,需要先做一些其他修改操作,然后在执行插入操作,由于插入数据可能会很多,用到多线程去拆分数据并行处理来提高响应时间,如果有一个线程执行失败&…...
设计(五:基于Carry4的高精度TDC设计))
基于FPGA的时间数字转换(TDC)设计(五:基于Carry4的高精度TDC设计)
1.基于Carry4进位链设计原理 常见的基于FPGA开发的TDC有直接计数法,多相位时钟采样法,抽头延迟线法等,之前内容为基于多相位的TDC,本章节中,主要讲解基于抽头延迟线法。在Xilinx FPGA开发中,实现抽头延迟线法有很多种,如使用IODELAY构建延迟进位链,此处将介绍基于Carr…...

【C++】二叉搜索树的实现(递归和非递归实现)
文章目录1、二叉搜索树1.1 构建二叉搜索树1.2 二叉搜索树的插入1.3 二叉搜索树的删除1.4 二叉搜索树插入和删除的递归实现为了学习map和set的底层实现,需要知道红黑树,知道红黑树之前需要知道AVL树。 红黑树和AVL树都用到了二叉搜索树结构,所…...

春招来了,如何正确使用领英超高效招聘海外员工、挖掘人才?
金三银四到了,每年的这个时候都是企业招聘的好时机。而领英是目前全球最大的职场社交网络平台,基本上海外求职都是在使用它,所以很多企业涉及到海外招聘时,都会优先考虑领英,但是却经常缺乏一些经验技巧,今…...

Mysql中锁机制深入理解
Mysql中锁机制深入理解默认大家已经知道。分类性能悲观锁,乐观锁操作类型读锁,写锁,数据粒度表锁,行锁,页面锁更细粒度间隙锁,临键锁按使用来讲。由数据粒度出发。表锁,分为 共享锁,…...

docker详细操作--未完待续
docker介绍 docker官网: Docker:加速容器应用程序开发 harbor官网:Harbor - Harbor 中文 使用docker加速器: Docker镜像极速下载服务 - 毫秒镜像 是什么 Docker 是一种开源的容器化平台,用于将应用程序及其依赖项(如库、运行时环…...

java_网络服务相关_gateway_nacos_feign区别联系
1. spring-cloud-starter-gateway 作用:作为微服务架构的网关,统一入口,处理所有外部请求。 核心能力: 路由转发(基于路径、服务名等)过滤器(鉴权、限流、日志、Header 处理)支持负…...

1688商品列表API与其他数据源的对接思路
将1688商品列表API与其他数据源对接时,需结合业务场景设计数据流转链路,重点关注数据格式兼容性、接口调用频率控制及数据一致性维护。以下是具体对接思路及关键技术点: 一、核心对接场景与目标 商品数据同步 场景:将1688商品信息…...

[10-3]软件I2C读写MPU6050 江协科技学习笔记(16个知识点)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16...

mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包
文章目录 现象:mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包遇到 rpm 命令找不到已经安装的 MySQL 包时,可能是因为以下几个原因:1.MySQL 不是通过 RPM 包安装的2.RPM 数据库损坏3.使用了不同的包名或路径4.使用其他包…...

【C++进阶篇】智能指针
C内存管理终极指南:智能指针从入门到源码剖析 一. 智能指针1.1 auto_ptr1.2 unique_ptr1.3 shared_ptr1.4 make_shared 二. 原理三. shared_ptr循环引用问题三. 线程安全问题四. 内存泄漏4.1 什么是内存泄漏4.2 危害4.3 避免内存泄漏 五. 最后 一. 智能指针 智能指…...

TSN交换机正在重构工业网络,PROFINET和EtherCAT会被取代吗?
在工业自动化持续演进的今天,通信网络的角色正变得愈发关键。 2025年6月6日,为期三天的华南国际工业博览会在深圳国际会展中心(宝安)圆满落幕。作为国内工业通信领域的技术型企业,光路科技(Fiberroad&…...

Vue ③-生命周期 || 脚手架
生命周期 思考:什么时候可以发送初始化渲染请求?(越早越好) 什么时候可以开始操作dom?(至少dom得渲染出来) Vue生命周期: 一个Vue实例从 创建 到 销毁 的整个过程。 生命周期四个…...

永磁同步电机无速度算法--基于卡尔曼滤波器的滑模观测器
一、原理介绍 传统滑模观测器采用如下结构: 传统SMO中LPF会带来相位延迟和幅值衰减,并且需要额外的相位补偿。 采用扩展卡尔曼滤波器代替常用低通滤波器(LPF),可以去除高次谐波,并且不用相位补偿就可以获得一个误差较小的转子位…...

Python 训练营打卡 Day 47
注意力热力图可视化 在day 46代码的基础上,对比不同卷积层热力图可视化的结果 import torch import torch.nn as nn import torch.optim as optim from torchvision import datasets, transforms from torch.utils.data import DataLoader import matplotlib.pypl…...
