电子技术——分立CS和CE放大器的低频响应
电子技术——分立CS和CE放大器的低频响应

我们之前在学习放大器中从来没有关系过信号频率对放大器的影响,也就是说我们默认放大器具有无限的带宽,这当然不符合现实逻辑。为了说明这一点,我们使用下图:
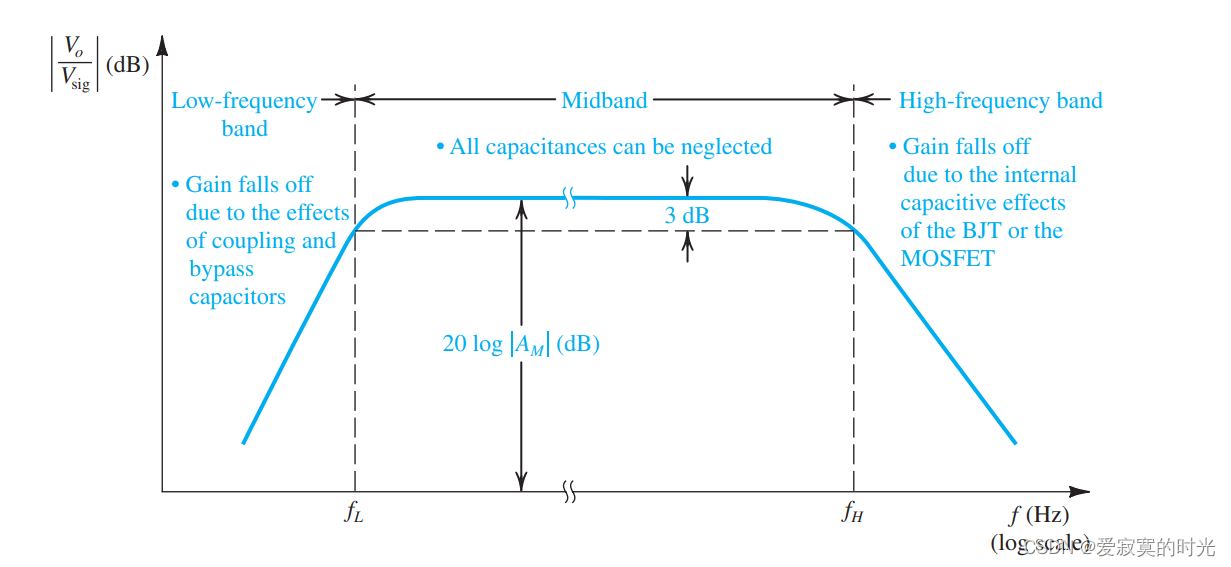
上图描述了MOS或BJT分立电路放大器的频率响应特性。我们发现存在中间一段区域,无论信号的频率怎么变化,放大器的增益都是一个常数。一般的放大器都工作在此区间,我们称这个区域为 中频带 。一个好的放大器设计应该让中频带处于我们想放大的信号频率上。如果不是这样,则放大器就会造成失真,因为不同频率的信号放大的倍数不同。
上图还展示了当信号频率较小的时候,放大器的增益就会下降。这是因为此时的耦合和旁路电容不在对信号具有低阻抗,回忆一下电容的阻抗为 1/jωC1/ j \omega C1/jωC 若信号频率越小,则阻抗越大。我们称 fLf_LfL 为中频带的低频结束点,经常被定义为中频带增益的 −3dB-3dB−3dB 下降点。我们本节将会讨论分立CS和CE放大器的低频响应。而对于集成电路来说,我们不使用耦合和旁路电容而是直接耦合,因此 fL=0f_L = 0fL=0 ,如图:
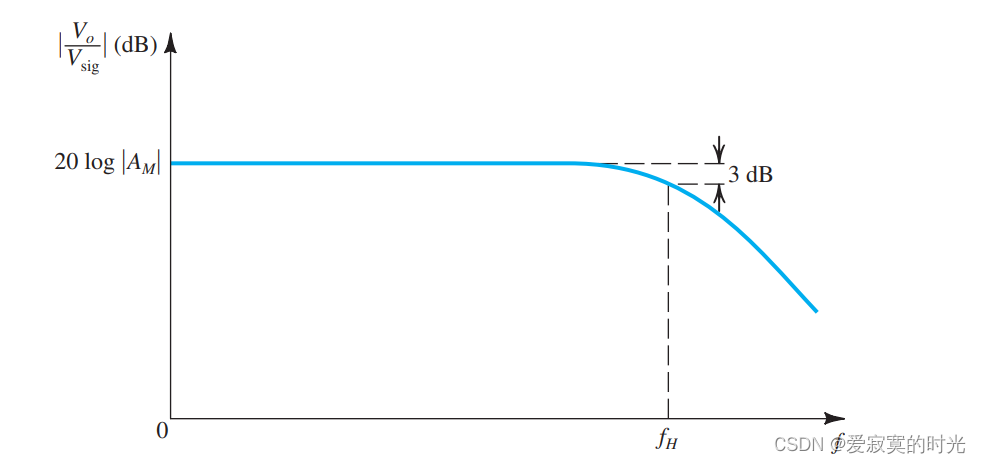
无论是分立电路放大器还是IC放大器都会存在一个中频带的高频结束点 fHf_HfH ,经常被定义为中频带增益的 −3dB-3dB−3dB 下降点,这是因为BJT和MOS的内部电容效应。我们将在后几个节学习如何在T模型或是混合 π\piπ 模型中模型化内部电容效应。
则放大器的 带宽 定义为:
BW=fH−fLBW = f_H - f_L BW=fH−fL
一个对于放大器非常重要的特性是 增益-带宽积 定义为:
GB=∣AM∣BWGB = |A_M|BW GB=∣AM∣BW
增益-带宽积通常被用来权衡一个放大器的增益和带宽。
在本节我们探究分立CS和CE放大器的低频响应。
CS放大器
下图展示了一个典型的分立CS放大器的完整结构:
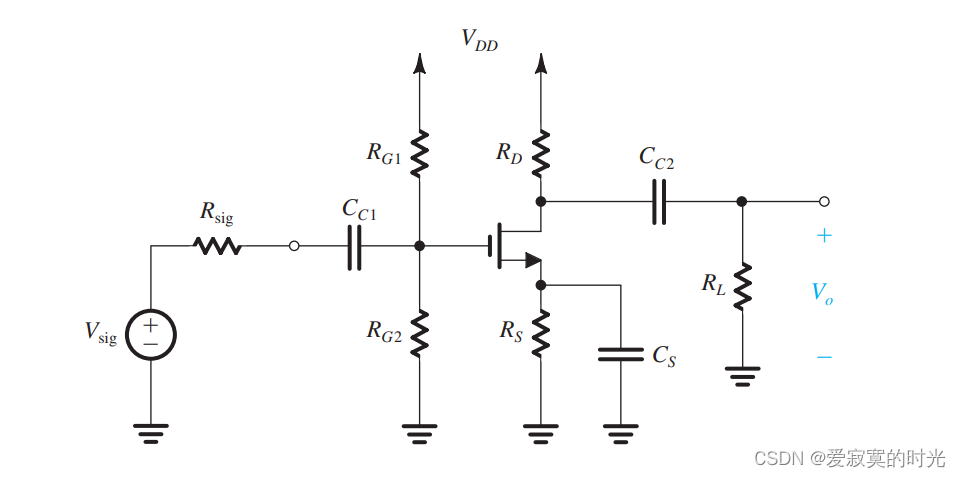
为了分析分立CS放大器在低频处的响应,我们使用下面的电路图进行研究:
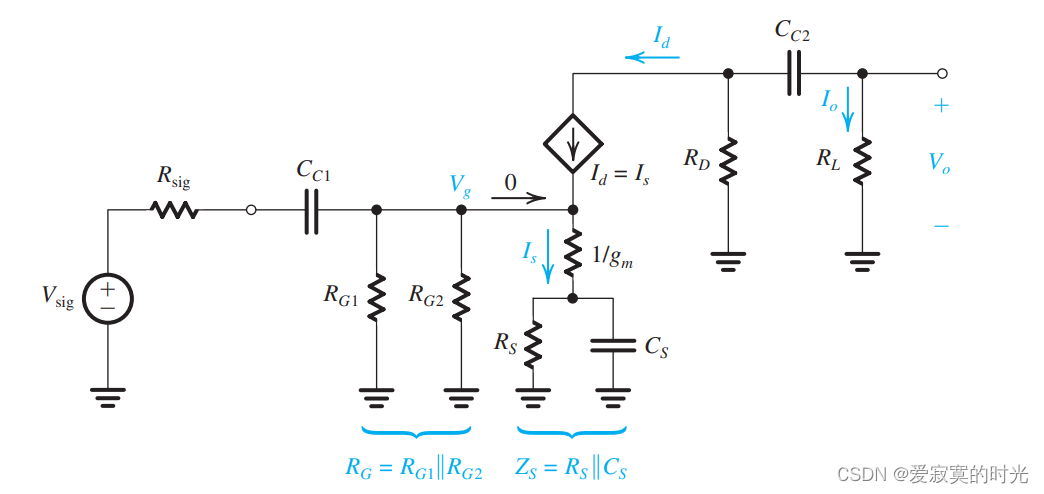
上图中,我们将 VDDV_{DD}VDD 短路,并且将MOS使用T模型替代。为了计算 Vo/VsigV_o / V_{sig}Vo/Vsig 我们使用下面的链式模型:
VoVsig=VgVsig×IdVg×VoId\frac{V_o}{V_{sig}} = \frac{V_g}{V_{sig}} \times \frac{I_d}{V_g} \times \frac{V_o}{I_d} VsigVo=VsigVg×VgId×IdVo
这里 VgV_gVg 是栅极电压, IdI_dId 是漏极电流。我们发现 VgV_gVg 可以通过分压定律计算:
Vg=VsigRGRG+1sCC1+RsigV_g = V_{sig} \frac{R_G}{R_G + \frac{1}{sC_{C1}} + R_{sig}} Vg=VsigRG+sCC11+RsigRG
这里的 RGR_GRG 是CS的输入阻抗为:
RG=RG1∣∣RG2R_G = R_{G1} || R_{G2} RG=RG1∣∣RG2
而 sss 是拉普拉斯变换中的复频率,以后我们都使用 sss 表示复频率:
s=jωs = j \omega s=jω
则重新排列:
VgVsig=RGRG+Rsigss+1CC1(RG+Rsig)\frac{V_g}{V_{sig}} = \frac{R_G}{R_G + R_{sig}} \frac{s}{s + \frac{1}{C_{C1}(R_G + R_{sig})}} VsigVg=RG+RsigRGs+CC1(RG+Rsig)1s
因此,我们发现 CC1C_{C1}CC1 在信号从信号源到MOS的栅极引入了频率相关因子。我们知道这个因子是单时间常数电路中高通型传递函数,具有极点频率:
ωP1=1CC1(RG+Rsig)\omega_{P1} = \frac{1}{C_{C1}(R_G + R_{sig})} ωP1=CC1(RG+Rsig)1
当 s=0s=0s=0 的时候, CC1C_{C1}CC1 引入了零因子。这是很显然的,因为电容具有阻直流的性质,下图描述了函数 ss+ωP1\frac{s}{s + \omega_{P1}}s+ωP1s 的频率响应波德图:
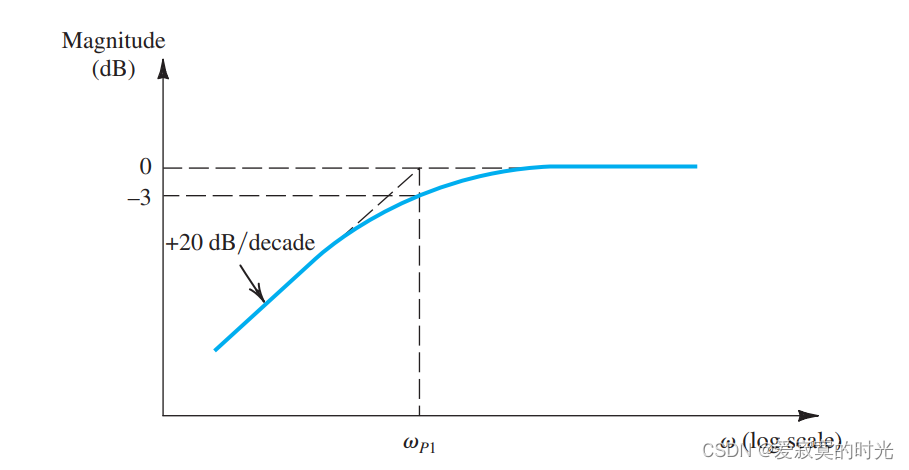
继续我们的 IdI_dId 分析,因为 Id=IsI_d = I_sId=Is 后者可以通过电压比源极阻抗算出来:
Id=Is=Vg1gm+ZS=gmVgYSgm+YSI_d = I_s = \frac{V_g}{\frac{1}{g_m} + Z_S} = g_mV_g \frac{Y_S}{g_m + Y_S} Id=Is=gm1+ZSVg=gmVggm+YSYS
这里:
YS=1ZS=1RS+sCSY_S = \frac{1}{Z_S} = \frac{1}{R_S} + sC_S YS=ZS1=RS1+sCS
写出多项式分式的形式:
IdVg=gms+1CSRSs+gm+1/RSCS\frac{I_d}{V_g} = g_m \frac{s + \frac{1}{C_SR_S}}{s + \frac{g_m + 1/R_S}{C_S}} VgId=gms+CSgm+1/RSs+CSRS1
也就是说,旁路电容引入了极点频率:
ωP2=gm+1/RSCS\omega_{P2} = \frac{g_m + 1/R_S}{C_S} ωP2=CSgm+1/RS
以及一个零点:
sZ=−1CSRSs_Z = -\frac{1}{C_SR_S} sZ=−CSRS1
对应的零点频率为:
ωZ=1CSRS\omega_Z = \frac{1}{C_SR_S} ωZ=CSRS1
下图展示了这个传递函数的频率响应图像:
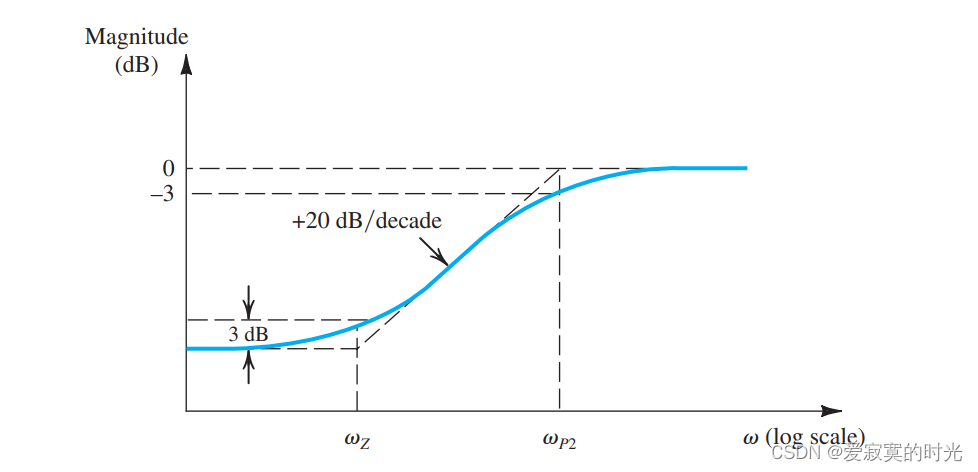
因为 gmg_mgm 很大,所以 ωP2>ωZ\omega_{P2} > \omega_ZωP2>ωZ 所以 ωP2\omega_{P2}ωP2 更加靠近中频带,对 ωL\omega_LωL 的影响比 ωZ\omega_ZωZ 大。
最后,计算:
VoId=−RDRLRD+RLss+1CC2(RD+RL)\frac{V_o}{I_d} = -\frac{R_DR_L}{R_D +R_L}\frac{s}{s + \frac{1}{C_{C2}(R_D+R_L)}} IdVo=−RD+RLRDRLs+CC2(RD+RL)1s
耦合电容 CC2C_{C2}CC2 引入极点频率:
ωP3=1CC2(RD+RL)\omega_{P3} = \frac{1}{C_{C2}(R_D+R_L)} ωP3=CC2(RD+RL)1
以及零点 s=0s=0s=0 (DC)。频率响应如下:
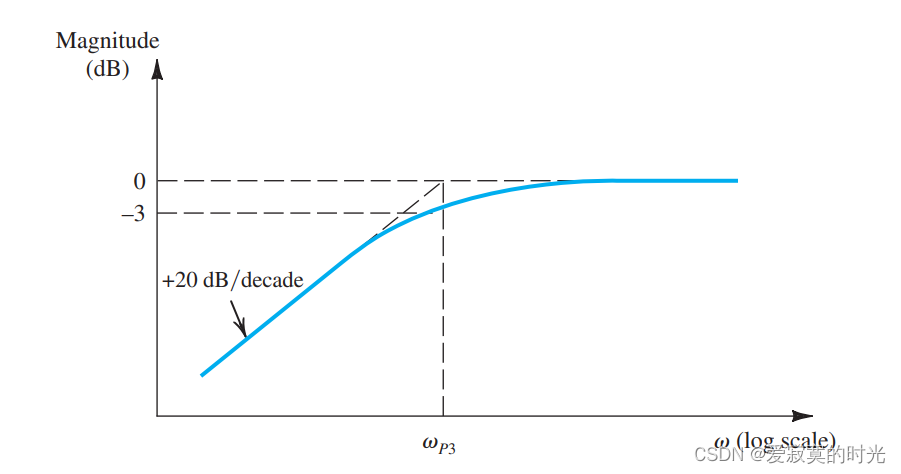
则整体低频响应函数为:
VoVsig=−RGRG+Rsiggm(RD∣∣RL)(ss+ωP1)(s+ωZs+ωP2)(ss+ωP3)\frac{V_o}{V_{sig}} = -\frac{R_G}{R_G + R_{sig}}g_m(R_D||R_L)(\frac{s}{s + \omega_{P1}})(\frac{s + \omega_Z}{s + \omega_{P2}})(\frac{s}{s + \omega_{P3}}) VsigVo=−RG+RsigRGgm(RD∣∣RL)(s+ωP1s)(s+ωP2s+ωZ)(s+ωP3s)
也就是:
VoVsig=AM(ss+ωP1)(s+ωZs+ωP2)(ss+ωP3)\frac{V_o}{V_{sig}} = A_M(\frac{s}{s + \omega_{P1}})(\frac{s + \omega_Z}{s + \omega_{P2}})(\frac{s}{s + \omega_{P3}}) VsigVo=AM(s+ωP1s)(s+ωP2s+ωZ)(s+ωP3s)
这里 AMA_MAM 为完美增益,即不考虑任何频率特性的增益系数,也是我们之前几章使用过的:
AM=−RGRG+Rsiggm(RD∣∣RL)A_M = -\frac{R_G}{R_G + R_{sig}}g_m(R_D||R_L) AM=−RG+RsigRGgm(RD∣∣RL)
当 s=jωs = j\omegas=jω 远大于 ωP1,ωP2,ωP3,ωZ\omega_{P1},\omega_{P2},\omega_{P3},\omega_ZωP1,ωP2,ωP3,ωZ 的时候,此时 Av≃AMA_v \simeq A_MAv≃AM 这个时候放大器进入中频带。
决定 3−dB3-dB3−dB 频率 fLf_LfL
有了上述推导出的公式,我们就可以确定CS放大器的中频带的低频结束点,当 ∣Vo/Vsig∣|V_o/V_{sig}|∣Vo/Vsig∣ 降至 ∣AM∣/2|A_M| / \sqrt{2}∣AM∣/2 的时候此时增益下降 3dB3dB3dB ,记为 fLf_LfL 。
有一个更简单的方式估算频率 fLf_LfL ,当所有的极点和零点分的足够开的时候,我们可以使用博德规则,整体博德图如下:
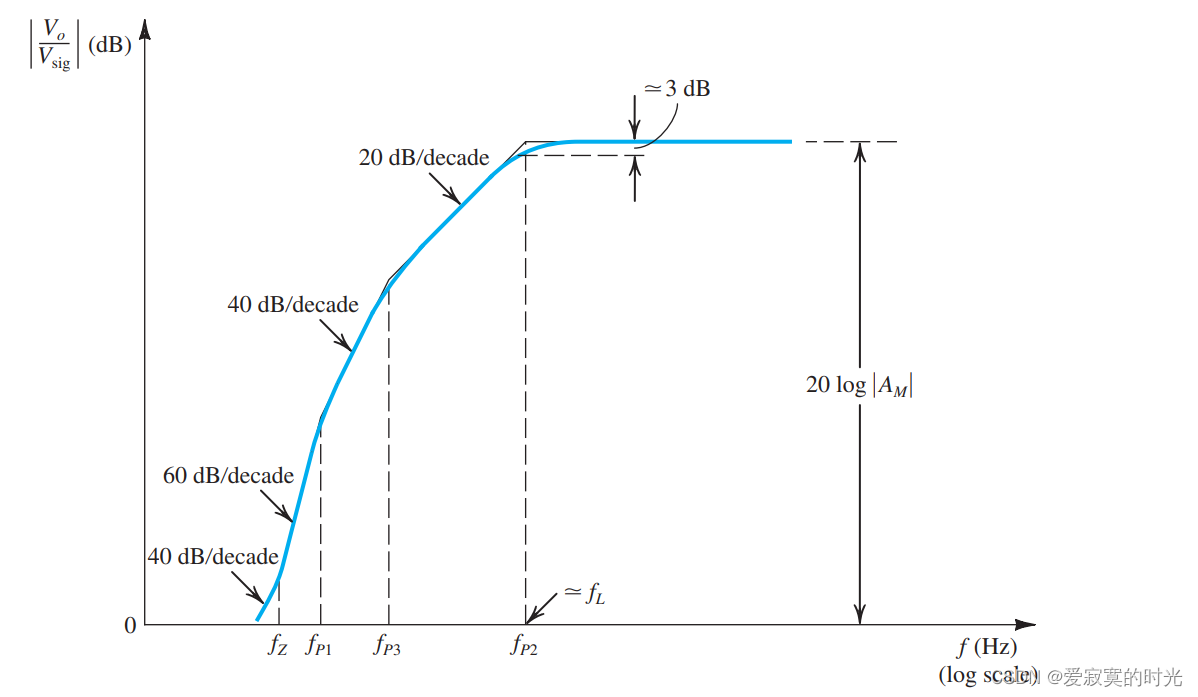
上图中,一般情况下都是 fP2f_{P2}fP2 最大。一个快速的估算方法为:若最高极点频率 fP2f_{P2}fP2 至少是最近的极点、零点频率 fP3f_{P3}fP3 的4倍(2个8度)。则 fLf_LfL 大约是最高极点频率。
fL=fP2f_L = f_{P2} fL=fP2
此时这种情况下,我们称最高极点频率为 主导极点 。
如果主导极点不存在,可以使用下面的表达式估算:
fL≃fP12+fP22+fP32−2fZ2f_L \simeq \sqrt{f_{P1}^2 + f_{P2}^2 + f_{P3}^2 - 2f_Z^2} fL≃fP12+fP22+fP32−2fZ2
通过观察决定极点和零点频率
因为在CS放大器中,各个电容是相互独立的,因此存在一个更简单的方法确定每一个电容的极点和零点频率。
首先是零点。传递函数的传输零点在 sss 使得 Vo=0V_o = 0Vo=0 的时候。在CS放大器中, CC1C_{C1}CC1 在 s=0s =0s=0 的时候具有无穷大阻抗因此引入了传输零点。
对于 CC2C_{C2}CC2 也具有相同的结论。然而,对于旁路电容 CSC_SCS 则具有不同的效果:根据定义传输零点在 sss 使得 ZS=∞Z_S = \inftyZS=∞ 的时候,此时 sZ=−1CSRSs_Z = -\frac{1}{C_SR_S}sZ=−CSRS1 。
对于极点,我们令 Vsig=0V_{sig} = 0Vsig=0 此时电路可以拆成下面三个电路:
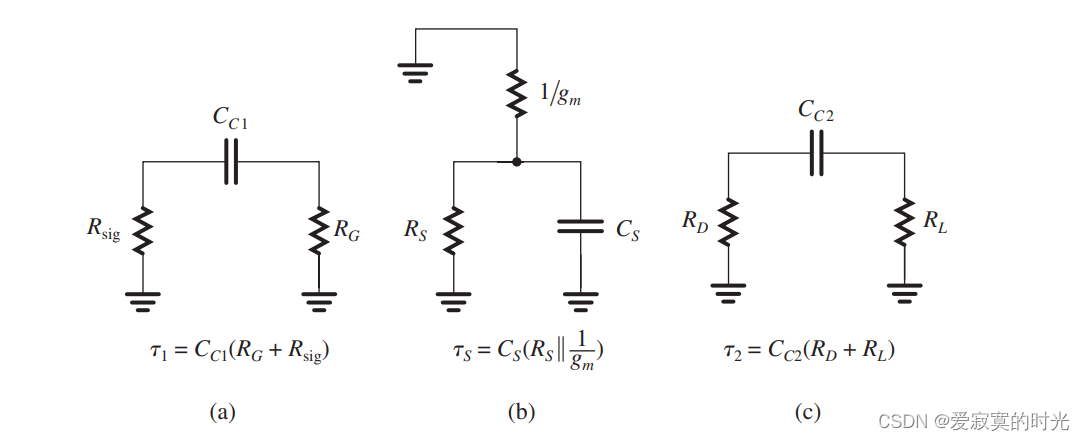
我们发现每一个电路都是单时间常数电路,时间常数为每个电容的容值乘以从该电容看过去的阻值,其对应的极点频率正好的每一个单时间常数的倒数。
耦合电容和旁路电容的选值
我们现在解决如何选择三个电容的容值,我们的最终目标是将 fLf_LfL 设定在我们想要的值上同时最小化三个电容的容值。因为从 CSC_SCS 看过去的阻值 1gm∣∣RS\frac{1}{g_m} || R_Sgm1∣∣RS 是三个里面最小的,总容抗可以通过选择 CSC_SCS 来提供一个最高的极点频率来最小化,也就是令 fP2=fLf_{P2} = f_LfP2=fL 。之后我们决定后两个极点频率,都是小于 fP2f_{P2}fP2 5到10倍的。然而,fP1f_{P1}fP1 和 fP3f_{P3}fP3 也不能设置的太小,因为这需要更大的 CC1,CC2C_{C1},C_{C2}CC1,CC2 。
短路时间常数法
在一些电路中,例如我们即将要讨论的CE放大器电路,电容并不是相互独立的,此时决定极点频率是比较困难的。幸好,存在一个简单的方法用来估算 fLf_LfL ,这个方法不需要计算极点频率。尽管这个方法需要建立在存在一个主导极点频率的前提下,但是在前提不是那么严格的情况下也能获得不错的结果。方法是:
- 令输入信号源 Vsig=0V_{sig} = 0Vsig=0 。
- 依次考虑每一个电容。就是说,当考虑电容 CiC_iCi 的时候,将其他电容看成是容值无穷大的电容,即短路状态。
- 对于每一个电容,计算从这个电容看过去的总阻值 RiR_iRi 这可以通过戴维南定理计算。
- 则 fL=∑i=1n1CiRif_L = \sum_{i = 1}^n \frac{1}{C_i R_i}fL=∑i=1nCiRi1
这个方法揭示了每个电容对 fLf_LfL 的贡献。
CE放大器
下图展示了一个完整的CE放大器的原理图:
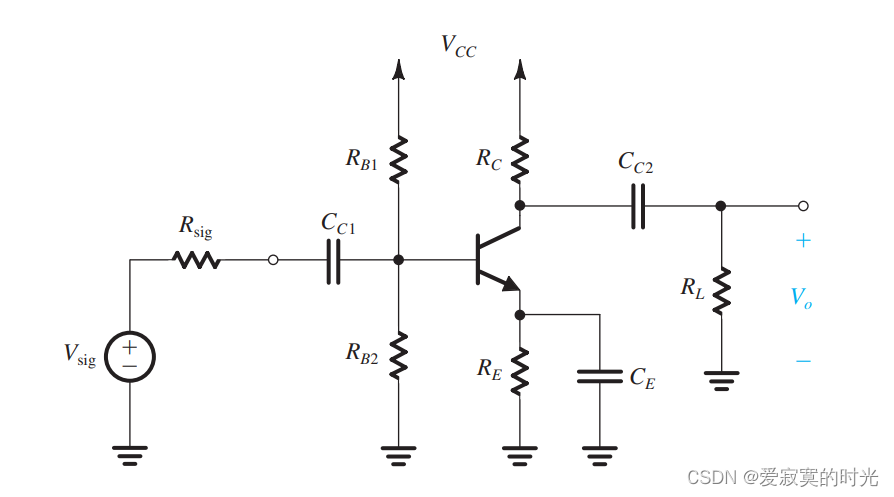
为了分析低频响应,我们使用下面的等效电路:
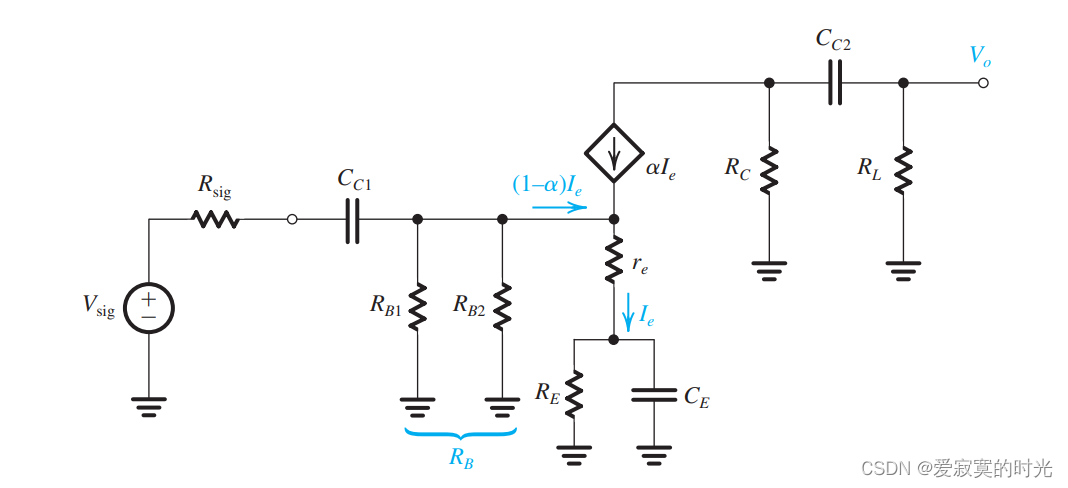
我们发现,因为存在有限的基极电流,电容 CC1C_{C1}CC1 和 CC2C_{C2}CC2 不是相互独立的。也就是说,不像CS放大器,每一个极点频率都和这两个电容有关,这给我们设计电路造成了不小的困难。因此,我们不想计算极点频率,而是转手使用短路时间常数法。
将信号输入源置地,然后依次考虑每个电容,如下图:
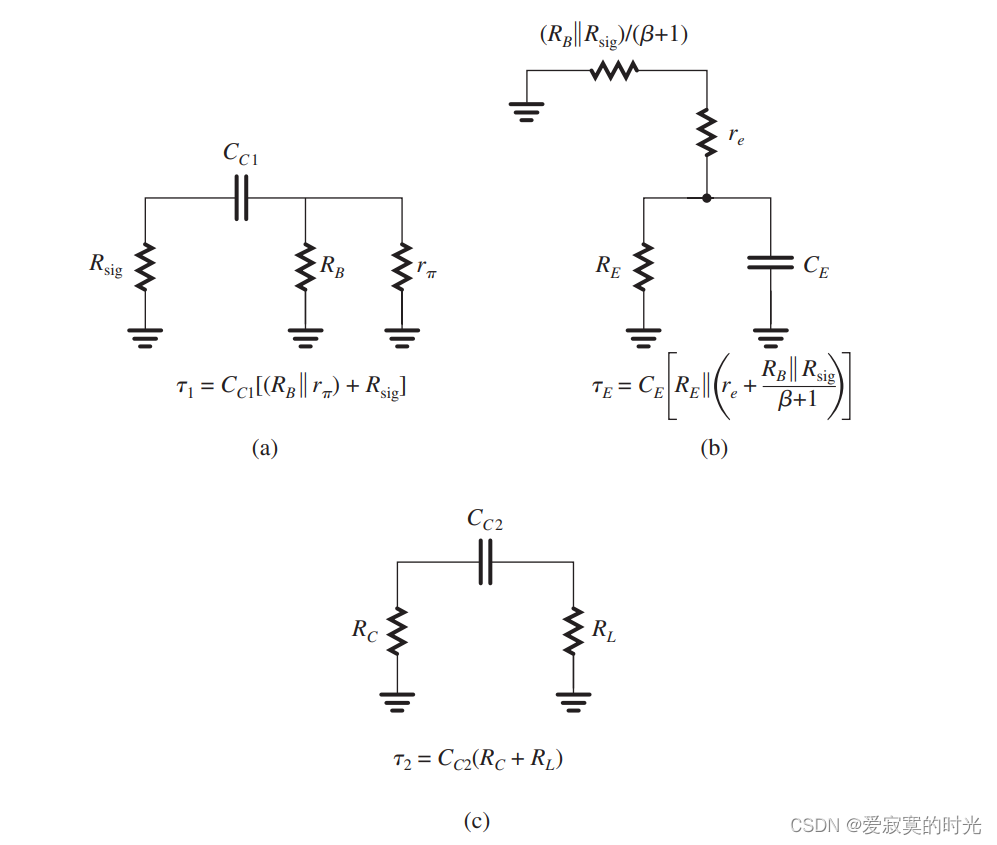
所有的时间常数我们都已经标在图中,因此估算的 fLf_LfL 为:
fL=12π[1CC1RC1+1CERE+1CC2RC2]f_L = \frac{1}{2 \pi}[\frac{1}{C_{C1} R_{C1}} + \frac{1}{C_E R_E} + \frac{1}{C_{C2} R_{C2}}] fL=2π1[CC1RC11+CERE1+CC2RC21]
这个式子揭示了每个电容对 fLf_LfL 的贡献。也就是具有最小时间常数的对 fLf_LfL 的贡献最大,换句话说,就是 CEC_ECE 贡献最大,因此 CEC_ECE 是我们的主导极点频率。通常计算我们都假设 CEC_ECE 对 fLf_LfL 贡献 80%80\%80% 而其他两项贡献 20%20\%20% 。
相关文章:

电子技术——分立CS和CE放大器的低频响应
电子技术——分立CS和CE放大器的低频响应 我们之前在学习放大器中从来没有关系过信号频率对放大器的影响,也就是说我们默认放大器具有无限的带宽,这当然不符合现实逻辑。为了说明这一点,我们使用下图: 上图描述了MOS或BJT分立电路…...

代码随想录【Day16】| 104. 二叉树的最大深度、111. 二叉树的最小深度、222. 完全二叉树的节点个数
104. 二叉树的最大深度 题目链接 题目描述: 给定一个二叉树,找出其最大深度。 二叉树的深度为根节点到最远叶子节点的最长路径上的节点数。 说明: 叶子节点是指没有子节点的节点。 示例: 给定二叉树 [3,9,20,null,null,15,7],…...

状态机图、通信图题
1.下列关于通信图与顺序图中的对象的相同点的叙述.正确的是(D)。A.两种图中都可以表示对象的创建和销毁B.对象在两种图中的位置都没有任何限制C.对象在两种图中的表示方式完全一致D.对象名在两种图中的表示完全一致2.下列关于通信图的说法错误的是(C)。A.通信图是对一次交互过程…...

分布式文件存储Minio学习入门
文章目录一、分布式文件系统应用场景1. Minio介绍Minio优点2. MinIO的基础概念、3. 纠删码ES(Erasure Code)4. 存储形式5. 存储方案二、Docker部署单机Minio三、minio纠删码模式部署四、分布式集群部署分布式存储可靠性常用方法冗余校验分布式Minio优势运行分布式minio使用dock…...
handler解析(4)-Message及Message回收机制
Message中可以携带的信息 Message中可以携带的数据比较丰富,下面对一些常用的数据进行了分析。 /*** 用户定义的消息代码,以便当接受到消息是关于什么的。其中每个Hanler都有自己的命名控件,不用担心会冲突*/ public int what; /*** 如果你…...

Linux使用定时任务监控java进程并拉起
需求描述: 设计一个脚本,通过Linux定时任务,每分钟执行一次,监控jar包进程是否存在,存在则不做动作,不存在则重新拉起jar包程序。 定时任务配置: */1 * * * * bash -x /root/myfile/jars/che…...
Win 10电脑摄像头提示错误代码0xa00f4244怎么办?
如果你的Windows 10电脑无法打开摄像头,提示“我们找不到你的摄像头”的错误消息,错误代码是0xA00F4244,原因可能是杀毒软件阻止了摄像头,或者是摄像头驱动程序有问题。 小编为你整理了摄像头错误代码0xA00F4244的解决方法&#…...
MFC消息机制
1.消息映射消息映射是一个将消息和成员函数相互关联的表。比如,框架窗口接收到一个鼠标左击消息,MFC将搜索该窗口的消息映射,如果存在一个处理WM_LBUTTTONDOWN消息的处理程序,然后就调用OnButtonDown。2.消息映射机制2.1 声明宏 写…...

全国计算机等级考试报名照片要求以及证件照制作教程
马上就全国计算机等级考试就要开始了,相信现在很多同学都在网上进行报名呢,报名的时候肯定需要用到个人证件照片,所以问题来了,我们怎么自己制作证件照片呢?计算机等级考试报名时对证件照都有哪些要求呢?该…...

SQLSERVER 临时表和表变量到底有什么区别?
一:背景 1. 讲故事 今天和大家聊一套面试中经常被问到的高频题,对,就是 临时表 和 表变量 这俩玩意,如果有朋友在面试中回答的不好,可以尝试看下这篇能不能帮你成功迈过。 二:到底有什么区别 1. 前置思…...

技术生态异军突起,昇思MindSpore进入AI框架第一梯队
ChatGPT掀起的新一轮人工智能狂欢下,隐藏在背后的“大模型”正进入越来越多开发者的视野。 诚如几年前开始流行的一种说法:数据是燃料、模型是引擎、算力是加速器。ChatGPT的出现,恰如其分地诠释了数据、模型和算力的“化学反应”。而在其中…...

审批流、工作流、业务流
是业务流、工作流、审批流 业务流:即业务流程,指为了完成某项业务而进行的各种工作的有序组合 工作流:即工作流程,指为了完成某项工作而进行的各种动作的有序组合 审批流:即审批流程,是对某项工作的审批活动…...
如何利用知识库加强内部管理?
许多公司都知道需要有一个面向客户的知识库,以加强客户服务,提供更好的客户体验。 但是很多企业没有意识到的是,拥有一个内部知识库软件对于员工改善沟通和促进知识共享的重要性。 协作是组织成功的关键部分,通过明确的远景和使…...

饕餮 NFT 作品集来袭!
饕餮 NFT 作品集包含 Chili Game 创作的体验《饕餮》第一章中的角色。可以在 The Sandbox 农历新年活动期间(01/18/23 至 02/28/23)体验。 饕餮的故事植根于中国古代神话,主要灵感来自《山海经》,一个关于捉妖人「青蛙侠」的故事。…...

C++中的内存分区、引用、函数
内存分区模型 代码区 存放CPU执行的机器指令代码区是共享的且具有只读性 全局区 全局变量和静态变量都存放在此处全局区还包括了常量区、字符串常量和其他常量也存放在此该区域的数据在程序结束后由操作系统释放const修饰的局部变量并不算在全局区 栈区 由编译器自动分配和释放…...

关于angular表格total模板中一直为0
哈喽 小伙伴们大家好昨天在用angular得antdesign组件得table表格 我用total模板 结果,total一直为0这可是愁坏我了 <ng-template #totalTemplate let-total>找到 {{ total }} 条结果</ng-template>[nzShowTotal]"totalTemplate"最后找到原因了…...
多线程事务怎么回滚
背景介绍1,最近有一个大数据量插入的操作入库的业务场景,需要先做一些其他修改操作,然后在执行插入操作,由于插入数据可能会很多,用到多线程去拆分数据并行处理来提高响应时间,如果有一个线程执行失败&…...
设计(五:基于Carry4的高精度TDC设计))
基于FPGA的时间数字转换(TDC)设计(五:基于Carry4的高精度TDC设计)
1.基于Carry4进位链设计原理 常见的基于FPGA开发的TDC有直接计数法,多相位时钟采样法,抽头延迟线法等,之前内容为基于多相位的TDC,本章节中,主要讲解基于抽头延迟线法。在Xilinx FPGA开发中,实现抽头延迟线法有很多种,如使用IODELAY构建延迟进位链,此处将介绍基于Carr…...

【C++】二叉搜索树的实现(递归和非递归实现)
文章目录1、二叉搜索树1.1 构建二叉搜索树1.2 二叉搜索树的插入1.3 二叉搜索树的删除1.4 二叉搜索树插入和删除的递归实现为了学习map和set的底层实现,需要知道红黑树,知道红黑树之前需要知道AVL树。 红黑树和AVL树都用到了二叉搜索树结构,所…...

春招来了,如何正确使用领英超高效招聘海外员工、挖掘人才?
金三银四到了,每年的这个时候都是企业招聘的好时机。而领英是目前全球最大的职场社交网络平台,基本上海外求职都是在使用它,所以很多企业涉及到海外招聘时,都会优先考虑领英,但是却经常缺乏一些经验技巧,今…...

HTML 语义化
目录 HTML 语义化HTML5 新特性HTML 语义化的好处语义化标签的使用场景最佳实践 HTML 语义化 HTML5 新特性 标准答案: 语义化标签: <header>:页头<nav>:导航<main>:主要内容<article>&#x…...

Docker 运行 Kafka 带 SASL 认证教程
Docker 运行 Kafka 带 SASL 认证教程 Docker 运行 Kafka 带 SASL 认证教程一、说明二、环境准备三、编写 Docker Compose 和 jaas文件docker-compose.yml代码说明:server_jaas.conf 四、启动服务五、验证服务六、连接kafka服务七、总结 Docker 运行 Kafka 带 SASL 认…...

【快手拥抱开源】通过快手团队开源的 KwaiCoder-AutoThink-preview 解锁大语言模型的潜力
引言: 在人工智能快速发展的浪潮中,快手Kwaipilot团队推出的 KwaiCoder-AutoThink-preview 具有里程碑意义——这是首个公开的AutoThink大语言模型(LLM)。该模型代表着该领域的重大突破,通过独特方式融合思考与非思考…...

Java 加密常用的各种算法及其选择
在数字化时代,数据安全至关重要,Java 作为广泛应用的编程语言,提供了丰富的加密算法来保障数据的保密性、完整性和真实性。了解这些常用加密算法及其适用场景,有助于开发者在不同的业务需求中做出正确的选择。 一、对称加密算法…...
)
Android第十三次面试总结(四大 组件基础)
Activity生命周期和四大启动模式详解 一、Activity 生命周期 Activity 的生命周期由一系列回调方法组成,用于管理其创建、可见性、焦点和销毁过程。以下是核心方法及其调用时机: onCreate() 调用时机:Activity 首次创建时调用。…...

在QWebEngineView上实现鼠标、触摸等事件捕获的解决方案
这个问题我看其他博主也写了,要么要会员、要么写的乱七八糟。这里我整理一下,把问题说清楚并且给出代码,拿去用就行,照着葫芦画瓢。 问题 在继承QWebEngineView后,重写mousePressEvent或event函数无法捕获鼠标按下事…...

NPOI Excel用OLE对象的形式插入文件附件以及插入图片
static void Main(string[] args) {XlsWithObjData();Console.WriteLine("输出完成"); }static void XlsWithObjData() {// 创建工作簿和单元格,只有HSSFWorkbook,XSSFWorkbook不可以HSSFWorkbook workbook new HSSFWorkbook();HSSFSheet sheet (HSSFSheet)workboo…...

HubSpot推出与ChatGPT的深度集成引发兴奋与担忧
上周三,HubSpot宣布已构建与ChatGPT的深度集成,这一消息在HubSpot用户和营销技术观察者中引发了极大的兴奋,但同时也存在一些关于数据安全的担忧。 许多网络声音声称,这对SaaS应用程序和人工智能而言是一场范式转变。 但向任何技…...

论文阅读:LLM4Drive: A Survey of Large Language Models for Autonomous Driving
地址:LLM4Drive: A Survey of Large Language Models for Autonomous Driving 摘要翻译 自动驾驶技术作为推动交通和城市出行变革的催化剂,正从基于规则的系统向数据驱动策略转变。传统的模块化系统受限于级联模块间的累积误差和缺乏灵活性的预设规则。…...

pycharm 设置环境出错
pycharm 设置环境出错 pycharm 新建项目,设置虚拟环境,出错 pycharm 出错 Cannot open Local Failed to start [powershell.exe, -NoExit, -ExecutionPolicy, Bypass, -File, C:\Program Files\JetBrains\PyCharm 2024.1.3\plugins\terminal\shell-int…...
