笔试题(十三):走迷宫
# 描述
# 定义一个二维数组 N*M ,如 5 × 5 数组下所示:
# int maze[5][5] = {
# 0, 1, 0, 0, 0,
# 0, 1, 1, 1, 0,
# 0, 0, 0, 0, 0,
# 0, 1, 1, 1, 0,
# 0, 0, 0, 1, 0,};
# 它表示一个迷宫,其中的1表示墙壁,0表示可以走的路,只能横着走或竖着走,不能斜着走,要求编程序找出从左上角到右下角的路线。入口点为[0,0],既第一格是可以走的路。
# 数据范围: 2≤n,m≤10 , 输入的内容只包含 0≤val≤1
# 输入描述:
# 输入两个整数,分别表示二维数组的行数,列数。再输入相应的数组,其中的1表示墙壁,0表示可以走的路。数据保证有唯一解,不考虑有多解的情况,即迷宫只有一条通道。
# 输出描述:
# 左上角到右下角的最短路径,格式如样例所示。
# 示例1
# 输入:
# 5 5
# 0 1 0 0 0
# 0 1 1 1 0
# 0 0 0 0 0
# 0 1 1 1 0
# 0 0 0 1 0
# 输出:
# (0,0)
# (1,0)
# (2,0)
# (2,1)
# (2,2)
# (2,3)
# (2,4)
# (3,4)
# (4,4)
def func(i, j, pos=[(0, 0)]):# 方法1if i == m - 1 and j == n - 1:for p in pos:print(p)return 1if j + 1 < n and a[i][j + 1] == 0: # 向右if (i, j + 1) not in pos:func(i, j + 1, pos + [(i, j + 1)])if j - 1 > 0 and a[i][j - 1] == 0: # 向左if (i, j - 1) not in pos:func(i, j - 1, pos + [(i, j - 1)])if i + 1 < m and a[i + 1][j] == 0: # 向下if (i + 1, j) not in pos:func(i + 1, j, pos + [(i + 1, j)])if i - 1 > 0 and a[i - 1][j] == 0: # 向上if (i - 1, j) not in pos:func(i - 1, j, pos + [(i - 1, j)])def dfs(i, j):# 方法2# 用dx和dy分别来表示:向左, 向右, 向上, 向下dx = [0, 0, -1, 1]dy = [-1, 1, 0, 0]if i == m - 1 and j == n - 1:for pos in route:print('(' + str(pos[0]) + ',' + str(pos[1]) + ')')returnfor k in range(4):x = i + dx[k]y = j + dy[k]if 0 <= x < m and 0 <= y < n and map1[x][y] == 0:map1[x][y] = 1route.append((x, y))dfs(x, y)# 如果我们无法到达指定终点,则需要沿原路返回,再把标记过的路去掉:map[x][y]=0,route.pop(),# 直到到达当初的分岔路口,进入下一次选择。map1[x][y] = 0route.pop()else:returnif __name__ == '__main__':m = 5n = 5a = [[0, 0, 0, 0, 1],[0, 1, 1, 0, 0],[0, 1, 0, 0, 1],[0, 0, 1, 0, 0],[0, 1, 0, 1, 0]]func(0, 0)map1 = a.copy()route = [(0, 0)]map1[0][0] = 1dfs(0, 0)
相关文章:
:走迷宫)
笔试题(十三):走迷宫
# 描述 # 定义一个二维数组 N*M ,如 5 5 数组下所示: # int maze[5][5] { # 0, 1, 0, 0, 0, # 0, 1, 1, 1, 0, # 0, 0, 0, 0, 0, # 0, 1, 1, 1, 0, # 0, 0, 0, 1, 0,}; # 它表示一个迷宫,其中的1表示墙壁,0表示可以走的路&#…...

Gradle相关的知识学习
这里有一套博客文章写的比较通俗易懂:https://www.jianshu.com/p/8e1ddd19083a...
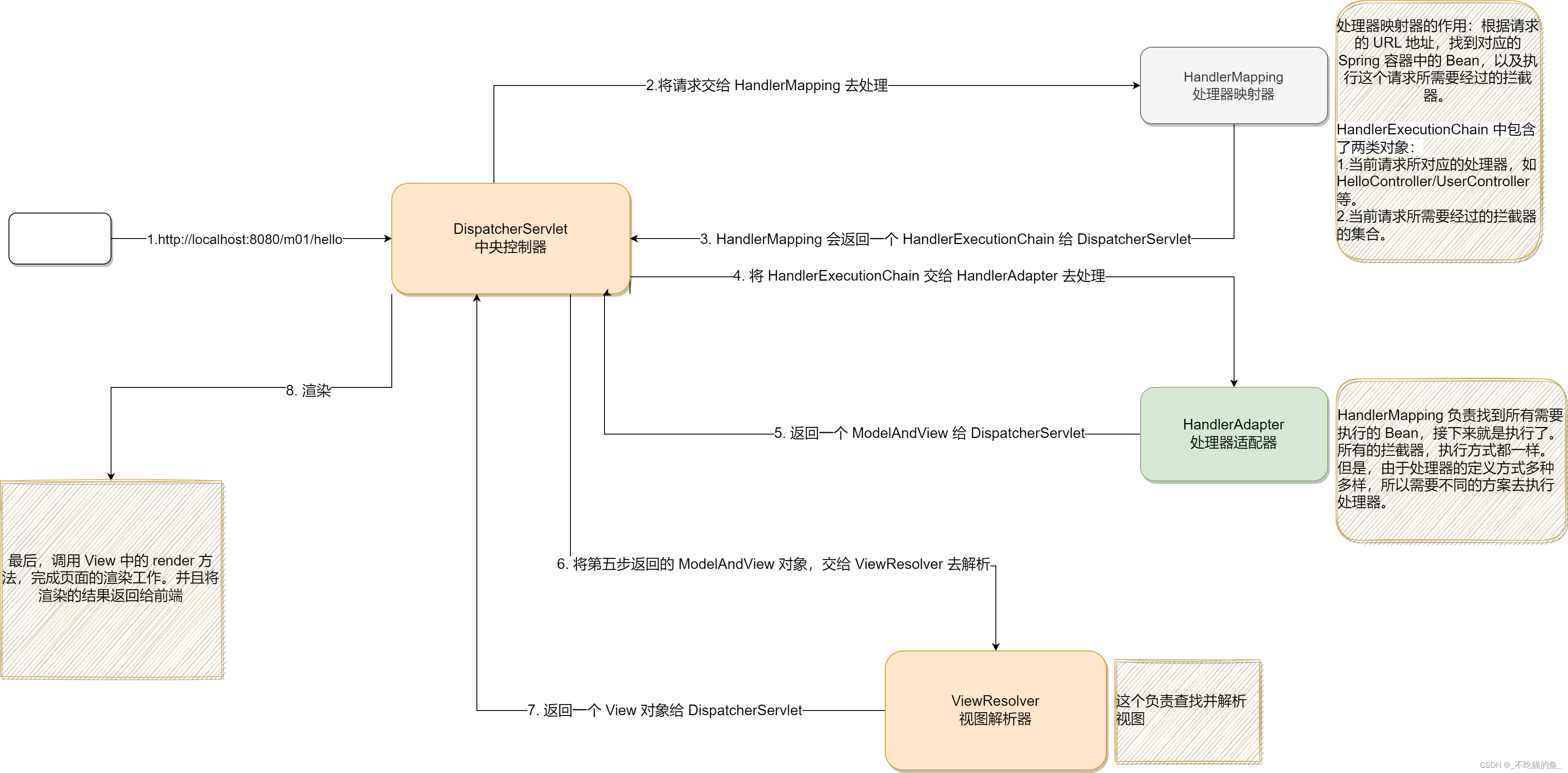
SpringMVC的工作原理
SpringMVC的工作原理流程图 SpringMVC流程 1、 用户发送请求至前端控制器DispatcherServlet。 2、 DispatcherServlet收到请求调用HandlerMapping处理器映射器。 3、 处理器映射器找到具体的处理器(可以根据xml配置、注解进行查找),生成处理器对象及处理器拦截…...
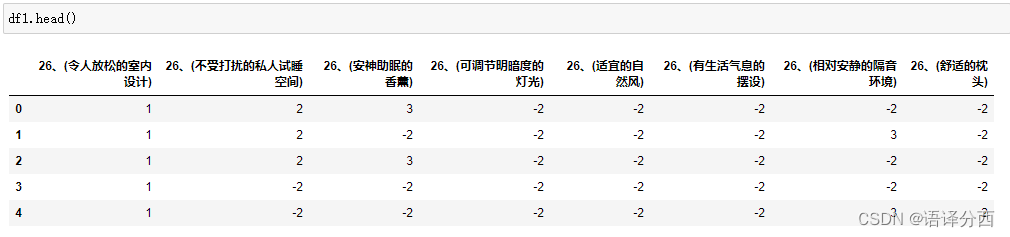
问卷数据分析流程
文章目录一、数据合并1. 读取数据2. 数据预览二、数据清洗1. 检验ID是否重复,剔除ID重复项2. 剔除填写时间小于xx分钟的值3.处理 量表题 一直选一个选项的问题三、数据清洗1.1 将问卷单选题的选项code解码,还原成原来的选项1.2 自动获取单选题旧的选项列…...

【观察】Solidigm P44 Pro SSD评测:原厂品质+软硬兼施=性能怪兽
众所周知,目前SSD(固态硬盘)已取代HDD(机械硬盘)成为电脑中常见的存储设备,特别是在技术创新的持续推动下,如今SSD的速度和效率都在不断地提高,从SATA2 3GB发展到SATA3 6GBÿ…...
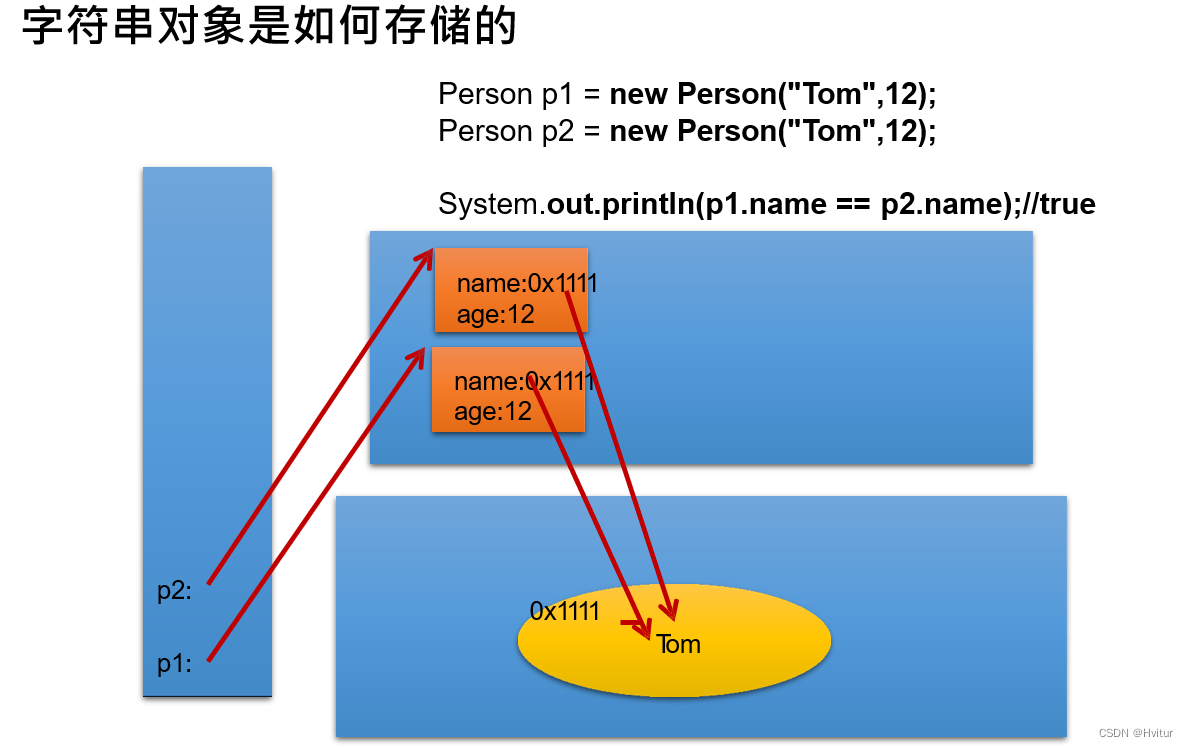
String对象的创建和比较
String类的概述 String类:代表字符串。 Java 程序中的所有字符串字面值(如 “abc” )都作 为此类的实例实现。 String是JDK中内置的一个类:java.lang.string 。 String表示字符串类型,属于引用数据类型,不…...
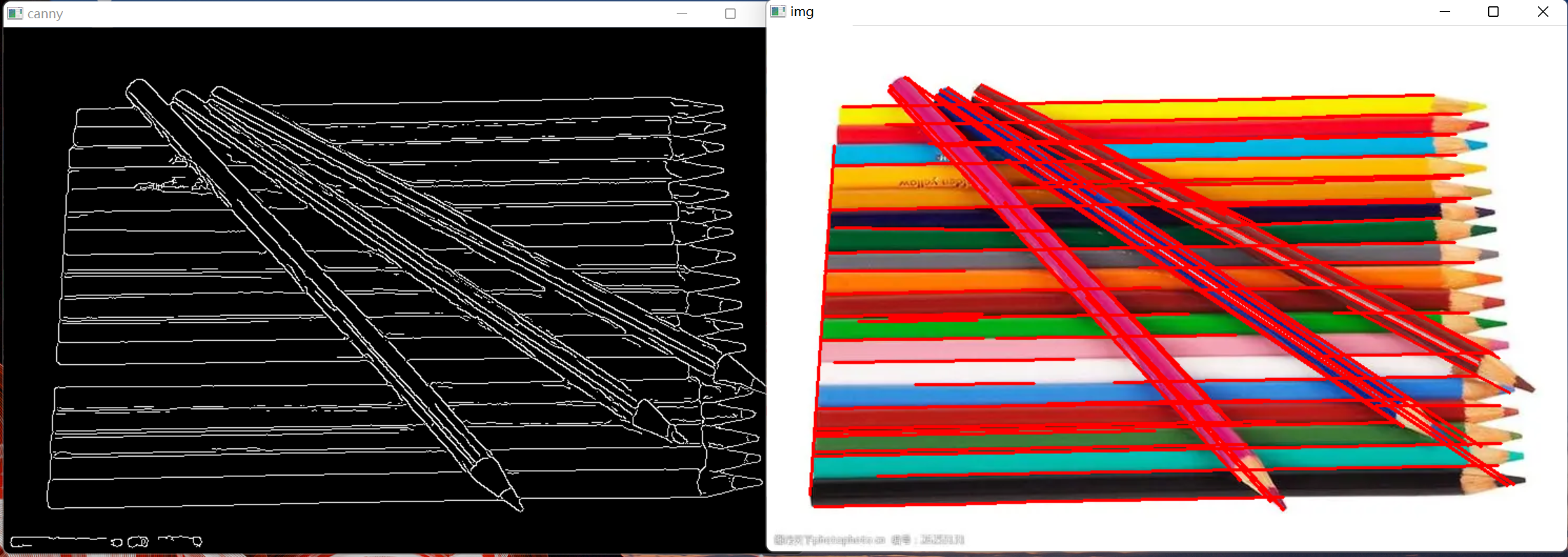
09 OpenCV图形检测
1 轮廓描边 cv2.findContours() 函数是OpenCV中用于寻找轮廓的函数之一。它可以用于在二值图像中查找并检测出所有的物体轮廓,以及计算出这些轮廓的各种属性,例如面积、周长、质心等。 cv2.findContours() 函数的语法如下: contours, hiera…...
解密Teradata与中国市场“分手”背后的原因!国产数据库能填补空白吗?
2月15日,西方的情人节刚刚过去一天,国内IT行业就爆出一个大瓜。 继Adobe、甲骨文、Tableau、Salesforce之后,又一个IT巨头要撤离中国市场。 Teradata天睿公司官宣与中国市场“分手”,结束在中国的直接运营。目前,多家…...

Bernstein-Vazirani算法
B-V算法 (1) 问题描述 给定布尔函数f:{0,1}n→0,1f:{\left\{ {0,1} \right\}^n} \to{0,1}f:{0,1}n→0,1, 函数fff的值是由输入比特串xxx和确定的比特串sss做模2意义下的内积:f(x)x⋅s(mod2),f\left( x \right) x \cdot s\left( {\bmod 2} \right),f(x)x⋅s(mod2),…...

华为OD机试 - 相对开音节 | 备考思路,刷题要点,答疑 【新解法】
最近更新的博客 【新解法】华为OD机试 - 关联子串 | 备考思路,刷题要点,答疑,od Base 提供【新解法】华为OD机试 - 停车场最大距离 | 备考思路,刷题要点,答疑,od Base 提供【新解法】华为OD机试 - 任务调度 | 备考思路,刷题要点,答疑,od Base 提供【新解法】华为OD机试…...
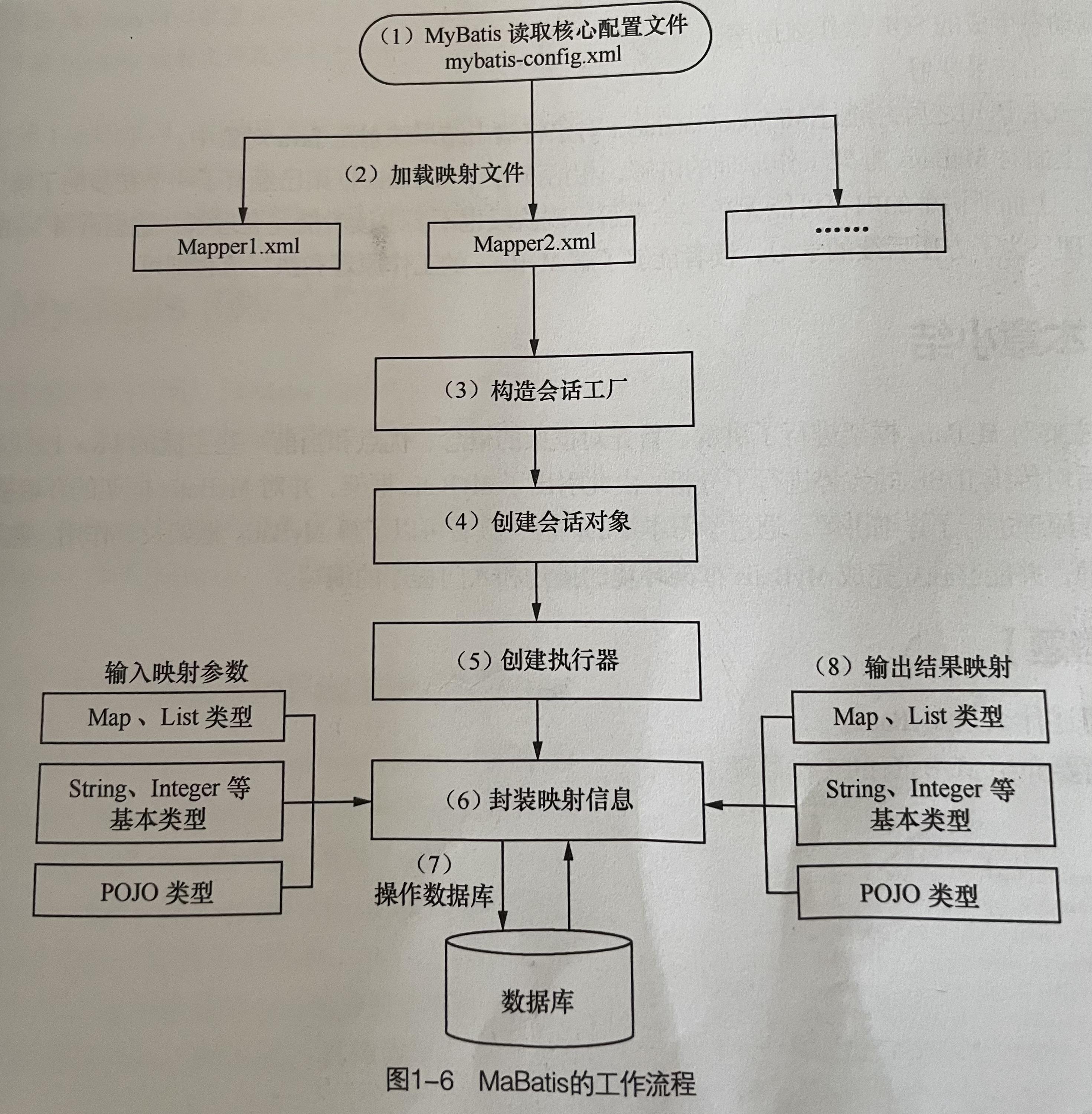
MyBatis
一、MyBatis环境搭建创建工程启动idea开发工具,选择工具栏中的“file”--“new”--“project”选项弹出“new project”对话框,编辑项目名称 选择maven项目,项目路径 单击 create 创建即可。引入相关依赖<dependencies><dependency&…...

良好的作息表
今天给大家带来“传说中”的“世界上最健康的作息时间表”(仅供参考),随时提醒自己吧,毕竟身体可是自己的哦。 7:30 起床:英国威斯敏斯特大学的研究人员发现,那些在早上5:22-7:21分起床的人,其血液中有一种能引起心脏病…...
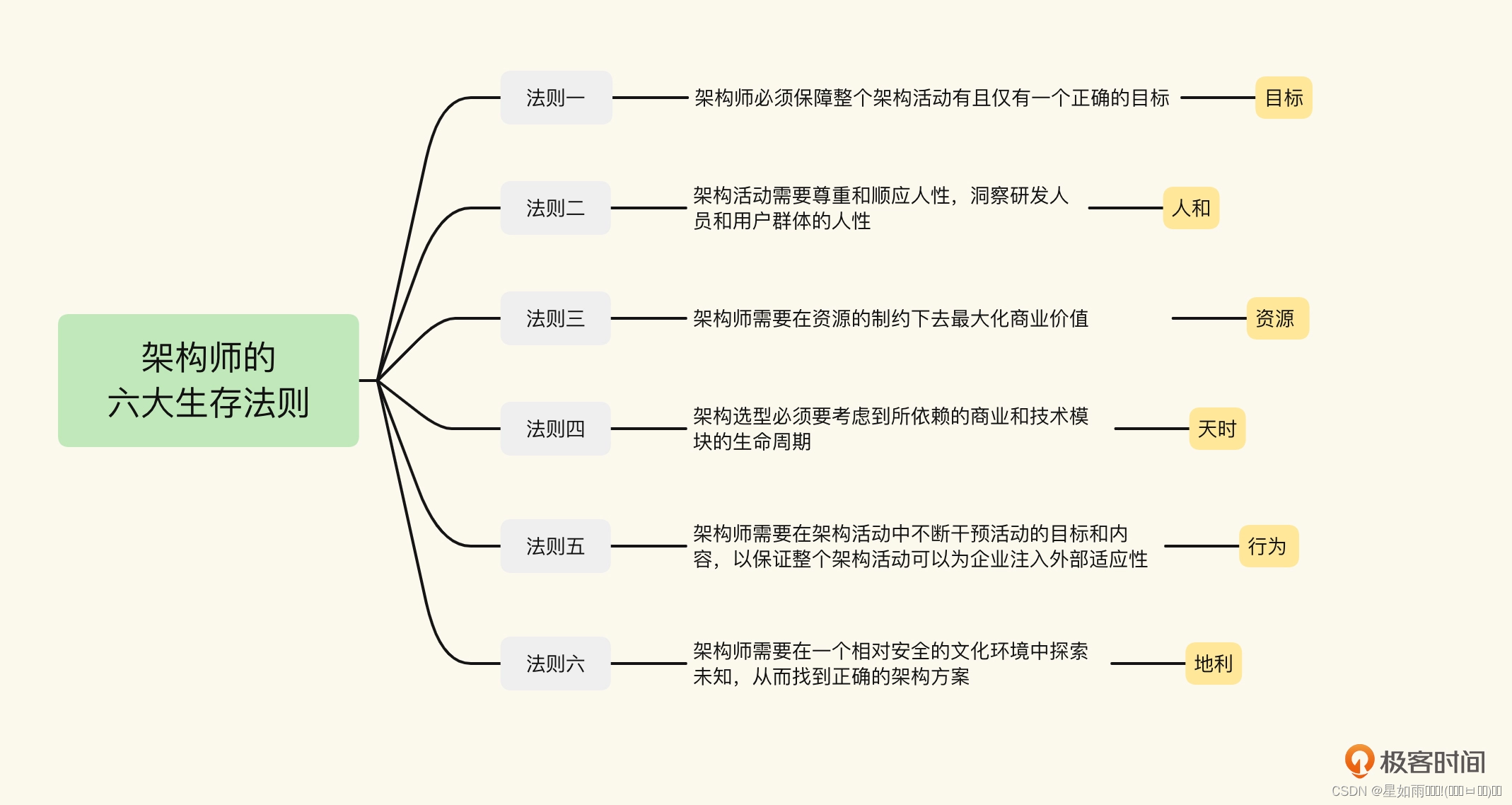
【郭东白架构课 模块一:生存法则】01|模块导学:是什么在影响架构活动的成败?
你好,我是郭东白。这节课是我们模块一的导入部分,我会先来介绍模块的主要内容,以及为什么我要讲生存法则这个话题。 一名软件架构师要为相对复杂的业务制定,并且引导实施一个结构化的软件方案。这个发现最终方案和推动实施的过程&…...

webshell免杀之函数与变量玩法
webshell免杀之函数与变量玩法 前言 前文列举了一些用符号免杀的例子,此篇文章就以函数和变量来尝试下免杀。 本文以PHP为例,用PHP中函数和变量及语法特性,在不隐藏函数关键字情况下进行免杀。 动态函数 PHP中支持一个功能叫 variable fu…...

【新解法】华为OD机试 - 去重求和 | 备考思路,刷题要点,答疑,od Base 提供
华为 OD 清单查看地址:blog.csdn.net/hihell/category_12199275.html 去重求和 | 备考思路,刷题要点,答疑,od Base 提供 给定一个数组,编写一个函数, 计算他的最大N个数和最小N个数的和, 需要对数组进行去重。 输入 第一行输入M,M表示数组大小 第二行输入M个数,表…...

MySQL 服务正在启动.MySQL 服务无法启动.服务没有报告任何错误。请键入 NET HELPMSG 3534 以获得更多的帮助。总结较全 (已解决)
输入以下命令启动mysql: net start mysql出现以下错误提示: MySQL 服务正在启动 .MySQL 服务无法启动。服务没有报告任何错误。请键入 NET HELPMSG 3534 以获得更多的帮助。 出现这个问题的话,一般有几个情况: 一、MySQL安装文…...

【数据结构与算法】数组2:双指针法 二分法(螺旋矩阵)
文章目录今日任务1.Leetcode977:有序数列的平方(1)题目(2)思路(3)暴力排序(4)双指针法2.Leetcode209:长度最小的子数组(1)题目&#x…...

librtmp优化
librtmp是一个RTMP的开源库,很多地方用它来做推流、拉流。它是RTMPDump开源软件里的一部分,librtmp的下载地址:RTMPDump,目前最新版是V2.3。本文重点介绍librtmp优化。 1、调整网络输出块大小。 RTMP_Connect0函数中LibRTMP是关…...

数据结构与算法(二):线性表
上一篇《数据结构与算法(一):概述》中介绍了数据结构的一些基本概念,并分别举例说明了算法的时间复杂度和空间复杂度的求解方法。这一篇主要介绍线性表。 一、基本概念 线性表是具有零个或多个数据元素的有限序列。线性表中数据…...
IOS安全区域适配
对于 iPhone 8 和以往的 iPhone,由于屏幕规规整整的矩形,安全区就是整块屏幕。但自从苹果手机 iphoneX 发布之后,前端人员在开发移动端Web页面时,得多注意一个对 IOS 所谓安全区域范围的适配。这其实说白了就是 iphoneX 之后的苹果…...

从零实现富文本编辑器#5-编辑器选区模型的状态结构表达
先前我们总结了浏览器选区模型的交互策略,并且实现了基本的选区操作,还调研了自绘选区的实现。那么相对的,我们还需要设计编辑器的选区表达,也可以称为模型选区。编辑器中应用变更时的操作范围,就是以模型选区为基准来…...

关于iview组件中使用 table , 绑定序号分页后序号从1开始的解决方案
问题描述:iview使用table 中type: "index",分页之后 ,索引还是从1开始,试过绑定后台返回数据的id, 这种方法可行,就是后台返回数据的每个页面id都不完全是按照从1开始的升序,因此百度了下,找到了…...

srs linux
下载编译运行 git clone https:///ossrs/srs.git ./configure --h265on make 编译完成后即可启动SRS # 启动 ./objs/srs -c conf/srs.conf # 查看日志 tail -n 30 -f ./objs/srs.log 开放端口 默认RTMP接收推流端口是1935,SRS管理页面端口是8080,可…...

智能仓储的未来:自动化、AI与数据分析如何重塑物流中心
当仓库学会“思考”,物流的终极形态正在诞生 想象这样的场景: 凌晨3点,某物流中心灯火通明却空无一人。AGV机器人集群根据实时订单动态规划路径;AI视觉系统在0.1秒内扫描包裹信息;数字孪生平台正模拟次日峰值流量压力…...
)
是否存在路径(FIFOBB算法)
题目描述 一个具有 n 个顶点e条边的无向图,该图顶点的编号依次为0到n-1且不存在顶点与自身相连的边。请使用FIFOBB算法编写程序,确定是否存在从顶点 source到顶点 destination的路径。 输入 第一行两个整数,分别表示n 和 e 的值(1…...

JAVA后端开发——多租户
数据隔离是多租户系统中的核心概念,确保一个租户(在这个系统中可能是一个公司或一个独立的客户)的数据对其他租户是不可见的。在 RuoYi 框架(您当前项目所使用的基础框架)中,这通常是通过在数据表中增加一个…...

视频行为标注工具BehaviLabel(源码+使用介绍+Windows.Exe版本)
前言: 最近在做行为检测相关的模型,用的是时空图卷积网络(STGCN),但原有kinetic-400数据集数据质量较低,需要进行细粒度的标注,同时粗略搜了下已有开源工具基本都集中于图像分割这块,…...

R语言速释制剂QBD解决方案之三
本文是《Quality by Design for ANDAs: An Example for Immediate-Release Dosage Forms》第一个处方的R语言解决方案。 第一个处方研究评估原料药粒径分布、MCC/Lactose比例、崩解剂用量对制剂CQAs的影响。 第二处方研究用于理解颗粒外加硬脂酸镁和滑石粉对片剂质量和可生产…...

安全突围:重塑内生安全体系:齐向东在2025年BCS大会的演讲
文章目录 前言第一部分:体系力量是突围之钥第一重困境是体系思想落地不畅。第二重困境是大小体系融合瓶颈。第三重困境是“小体系”运营梗阻。 第二部分:体系矛盾是突围之障一是数据孤岛的障碍。二是投入不足的障碍。三是新旧兼容难的障碍。 第三部分&am…...

打手机检测算法AI智能分析网关V4守护公共/工业/医疗等多场景安全应用
一、方案背景 在现代生产与生活场景中,如工厂高危作业区、医院手术室、公共场景等,人员违规打手机的行为潜藏着巨大风险。传统依靠人工巡查的监管方式,存在效率低、覆盖面不足、判断主观性强等问题,难以满足对人员打手机行为精…...
