领域搜索算法之经典The Lin-Kernighan algorithm
领域搜索算法之经典The Lin-Kernighan algorithm
- The Lin-Kernighan algorithm
- 关于算法性能提升的约束
- 参考文献
领域搜索算法是TSP问题中的三大经典搜索算法之一,另外两种分别是回路构造算法和组合算法。
而这篇文章要介绍的The Lin-Kernighan algorithm属于领域搜索算法。顾名思义,就是在已有的可行解的领域范围内进行搜索更好的解。
文章不是科普性的文章,专业性更强,开门见山。
LKH算法是对原有的3-opt算法的改进,速度更快,效率更高。
也是因为学习该算法,纠正了笔者之前对3-opt的错误理解,同时也作为学习笔记分享给大家
下面看算法的伪代码
The Lin-Kernighan algorithm
需要提前说明的是
问题背景是对称的TSP问题,图是无向完全图,距离矩阵是dij对称的
T是初始可行解,T=(t1,t2,t3,…,tn)
xi,表示T中边,yi表示不属于T中的边,i可取1-n
Gi表示,将xi替换成yi所得到的收益,即总花费是否减少

1.生成初始可行解T
2.置i=1,选择t1
3 选择x1为(t1,t2)且x1属于T,是T的边(注意算法中xi都属于T,yi都不属于T,xi是要从T中删除的边,
而yi是要加入T中以形成T‘的边)
这里的==选择==是穷举出所有可能的情况
4.同样选择y1不属于T,且G1>0(G1表示删去x1,加入y1所得到的收益为正,即花销减小了)
如果不满足则跳到12
5.令 i += 1
6.在T中选择xi=(t2i-1,t2i)且满足以下的条件
①t2i可以和t1直接相连,若是这样,就可直接构成新的T’,跳到2。②ys和以xi不相等
7.选择yi=(t2i,t2i+1)且不属于T,满足下面三个条件:
①Gi收益>0。②yi != xs(s为下标)。③xi+1是存在的
且又有,如果yi存在,跳到5
8.如果y2没有被穷举完,回到7
9.如果x2没有被穷举完,回到6
10.如果y1没有被穷举完,回到4
11.如果x1没有被穷举完,回到3
12.如果t1没有被穷举完,回到3
13.停止算法或者回到步骤1
以上是对算法的解释,下面对一些有疑难的地方进行重点输出自己的解释
该算法是逐步确定3-opt算法中的三天需要交换的边,顺序是x1,y1,x2,如果收益为正,则更新,否则找x1,y1,x3。如果收益为负,继续找x1,y2,x2,继续找x1,x2,y3.这是一层一层的像栈一样的顺序,所以才会有之后8-12的回溯操作,逐步回溯到问题的最开始,就像树的分支一样。
值得注意的是:LKH算法与原始的3-opt算法不一样的是,它参加交换的第三条边是不属于T的,即自己生成的。
随着时间和研究的推进,LKH的进一步改进也涌现出来,具体可以参看参考文献
关于算法性能提升的约束
用以上LKH算法寻优的过程中,还会遇到很多极端的情况,此时可以设置一些优化算法的约束,文献中用的语言比较抽象,笔者对其进行理解翻译和解释,当然还有其他约束有待发现和补充,要介绍的约束如下:
a 交换之后可以形成闭合回路
b T‘的收益为正
c 环路是闭合的(其实a和c很大一部分是重复的)
d 先前被取出的边不能加入,先前加入过的边不能被再删除
e yi=(t2i,t2i+1)的下一条边必须是和y2i的距离是最近的5个城市之一
f 对于i>=4时,xi中i下标较小的边不能再被拆分
g 寻优截止,当收益不再为正时
h 重新构成回路的时候,连接采用贪心的连接方法
参考文献
Helsgaun K. Version 1.2 (August 2001)[J].
相关文章:

领域搜索算法之经典The Lin-Kernighan algorithm
领域搜索算法之经典The Lin-Kernighan algorithmThe Lin-Kernighan algorithm关于算法性能提升的约束参考文献领域搜索算法是TSP问题中的三大经典搜索算法之一,另外两种分别是回路构造算法和组合算法。 而这篇文章要介绍的The Lin-Kernighan algorithm属于领域搜索算…...

深度学习基础-机器学习基本原理
本文大部分内容参考《深度学习》书籍,从中抽取重要的知识点,并对部分概念和原理加以自己的总结,适合当作原书的补充资料阅读,也可当作快速阅览机器学习原理基础知识的参考资料。 前言 深度学习是机器学习的一个特定分支。我们要想…...

C语言操作符详解 一针见血!
目录算数操作符移位操作符位操作符赋值操作符单目操作符关系操作符逻辑操作符条件操作符逗号表达式下标引用、函数调用和结构成员表达式求值11.1 隐式类型转换算数操作符💭 注意/ 除法 --得到的是商% 取模(取余)--得到的是余数如果除法操作符…...
前端面试题汇总
一:JavaScript 1、闭包是什么?利弊?如何解决弊端? 闭包是什么:JS中内层函数可以访问外层函数的变量,外层函数无法操作内存函数的变量的特性。我们把这个特性称作闭包。 闭包的好处: 隔离作用…...

以数据驱动管理场景,低代码助力转型下一站
数据驱动 数据驱动,是通过移动互联网或者其他的相关软件为手段采集海量的数据,将数据进行组织形成信息,之后对相关的信息讲行整合和提炼,在数据的基础上经过训练和拟合形成自动化的决策模型,简单来说,就是…...

2023年全国数据治理DAMA-CDGA/CDGP考试报名到弘博创新
弘博创新是DAMA中国授权的数据治理人才培养基地,贴合市场需求定制教学体系,采用行业资深名师授课,理论与实践案例相结合,快速全面提升个人/企业数据治理专业知识与实践经验,通过考试还能获得数据专业领域证书。 DAMA认…...

流程控制之循环
文章目录五、流程控制之循环5.1 步进循环语句for5.1.1 带列表的for循环语句5.1.2 不带列表的for循环语句5.1.3 类C风格的for循环语句5.2 while循环语句5.2.1 while循环读取文件5.2.2 while循环语句示例5.3 until循环语句5.4 select循环语句5.5 嵌套循环5.4 利用break和continue…...
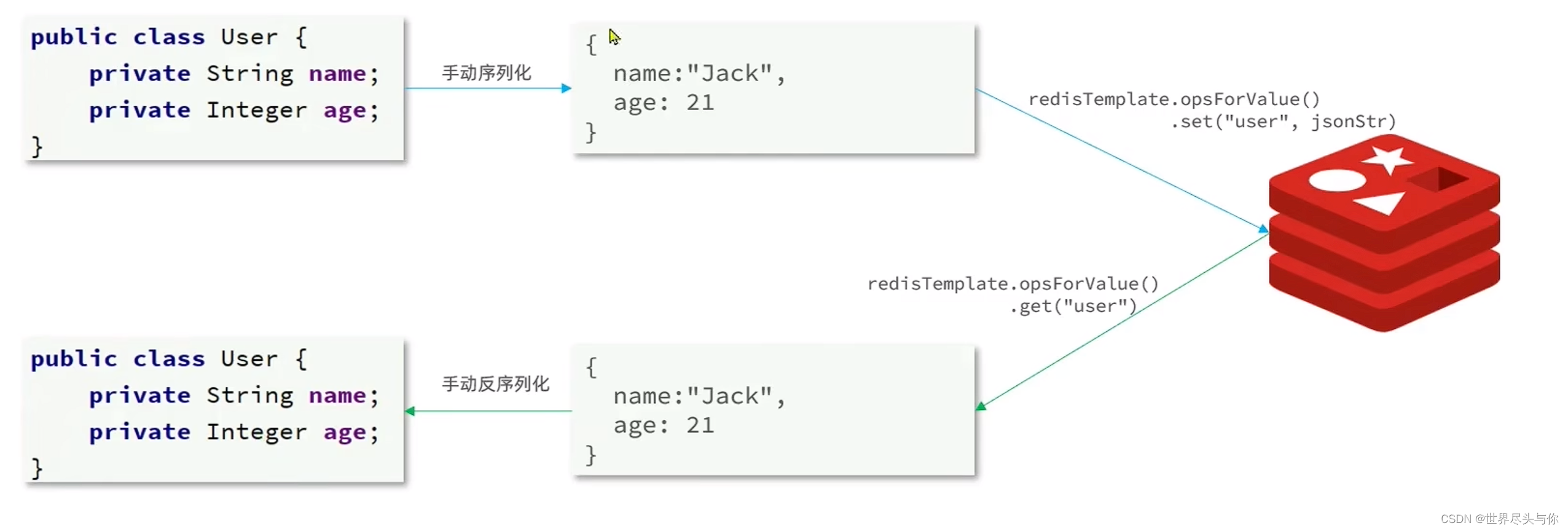
SpringDataRedis快速入门
SpringDataRedis快速入门1.SpringDataRedis简介2.RedisTemplate快速入门3.RedisSerializer4.StringRedisTemplate1.SpringDataRedis简介 SpringData是Spring中数据操作的模块,包含对各种数据库的集成,其中对Redis的集成模块就叫做SpringDataRedis Spri…...

MySQL 的执行计划 explain 详解
目录 什么是执行计划 执行计划的内容 select子句的类型 访问类型 索引的存在形式...
2023年网络安全比赛--Web综合渗透测试中职组(超详细)
一、竞赛时间 180分钟 共计3小时 二、竞赛阶段 1.通过URL访问http://靶机IP/1,对该页面进行渗透测试,将完成后返回的结果内容作为FLAG值提交; 2.通过URL访问http://靶机IP/2,对该页面进行渗透测试,将完成后返回的结果内容作为FLAG值提交; 3.通过URL访问http://靶机IP/3,对…...
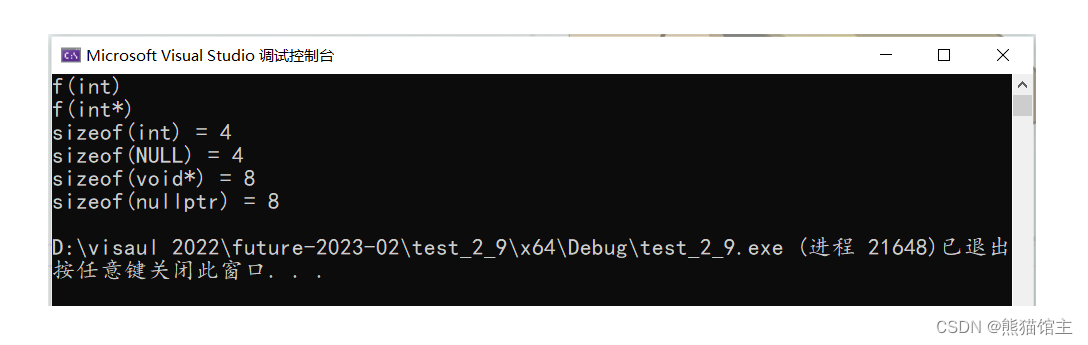
【c++之于c的优化 - 下】
前言 一、inline 概念 以inline修饰的函数叫做内联函数,编译时C编译器会在调用内联函数的地方展开,没有函数调用建立栈帧的开销,内联函数提升程序运行的效率。 如果在上述函数前增加inline关键字将其改成内联函数,在编译期间编译…...
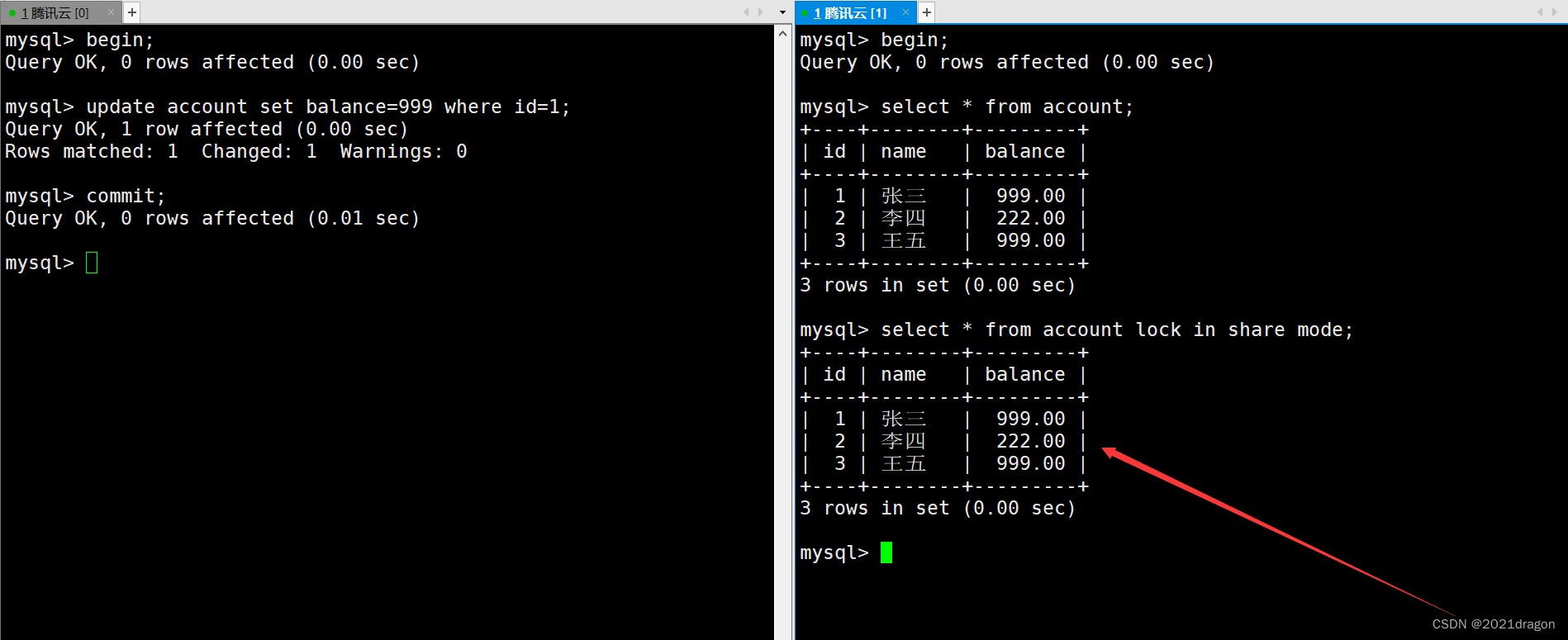
MySQL事务管理
文章目录MySQL事务管理事务的概念事务的版本支持事务的提交方式事务的相关演示事务的隔离级别查看与设置隔离级别读未提交(Read Uncommitted)读提交(Read Committed)可重复读(Repeatable Read)串行化&#…...

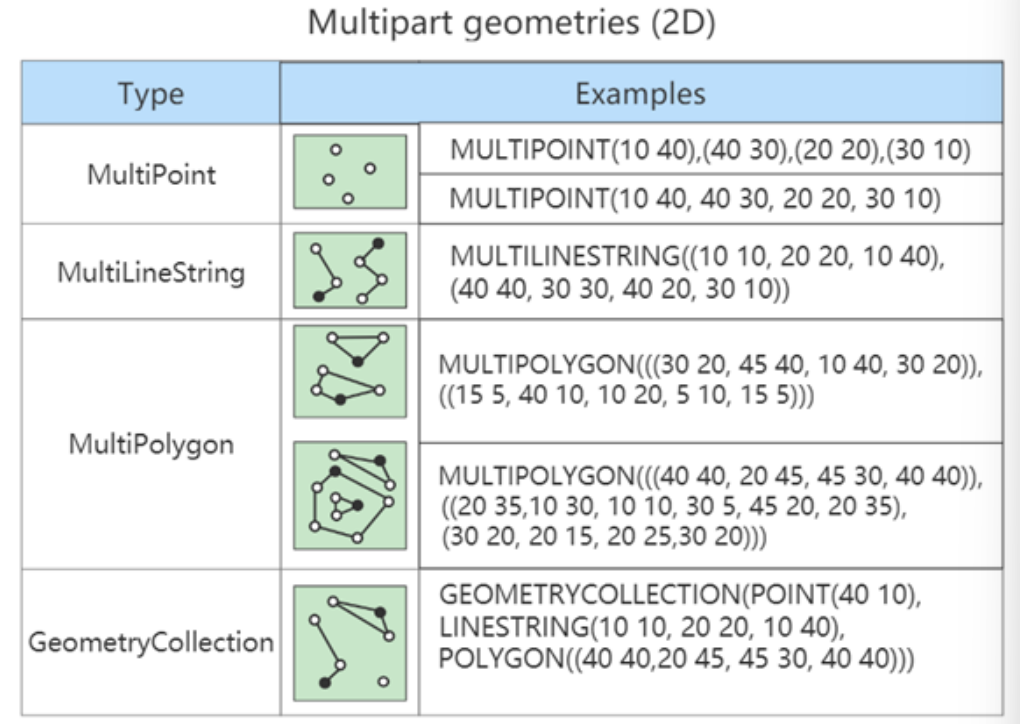
二维计算几何全家桶
参考文章:范神的神仙博客 前置芝士 一些高中数学 向量的叉积:向量的点积为 a⋅b∣a∣∣b∣cos<a,b>a\cdot b|a||b|\cos<a,b>a⋅b∣a∣∣b∣cos<a,b>,向量的叉积为 ab∣a∣∣b∣sin<a,b>a\times b|a||b|\sin<…...
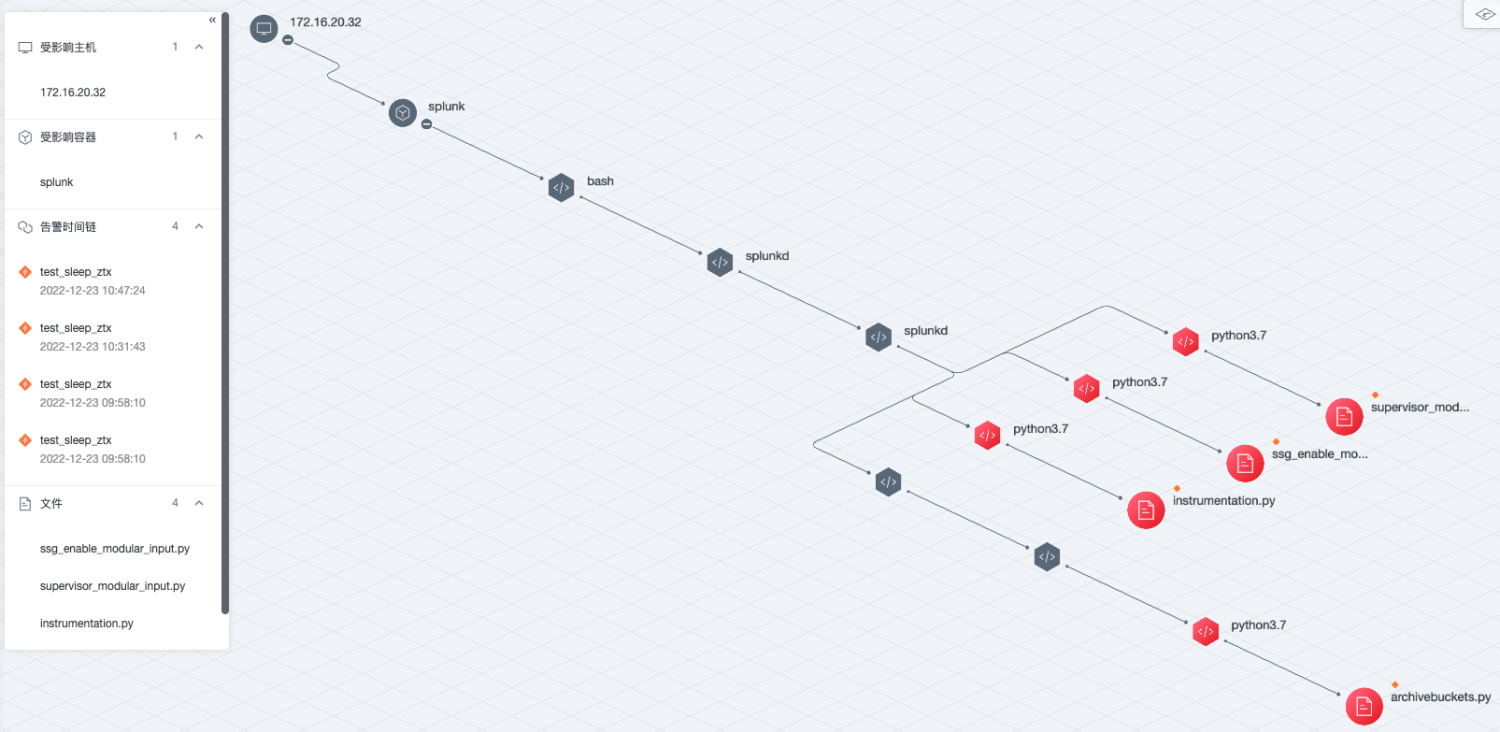
基于图的下一代入侵检测系统
青藤云安全是一家主机安全独角兽公司,看名字就知道当前很大一块方向专注云原生应用安全,目前主营的是主机万相/容器蜂巢产品,行业领先,累计支持 800万 Agent。当前公司基于 NebulaGraph 结合图技术开发的下一代实时入侵检测系统已…...

若依框架---树状层级部门数据库表
👏作者简介:大家好,我是小童,Java开发工程师,CSDN博客博主,Java领域新星创作者 📕系列专栏:前端、Java、Java中间件大全、微信小程序、微信支付、若依框架、Spring全家桶 Ǵ…...
【Mysql第十期 数据类型】
文章目录1. MySQL中的数据类型2.类型介绍2.2 可选属性2.2.2 UNSIGNED2.2.3 ZEROFILL2.3 适用场景2.4 如何选择?3. 浮点类型3.2 数据精度说明3.3 精度误差说明4. 定点数类型4.1 类型介绍4.2 开发中经验5. 位类型:BIT6. 日期与时间类型6.1 YEAR类型6.2 DAT…...

2023-2-9 刷题情况
删除子文件夹 题目描述 你是一位系统管理员,手里有一份文件夹列表 folder,你的任务是要删除该列表中的所有 子文件夹,并以 任意顺序 返回剩下的文件夹。 如果文件夹 folder[i] 位于另一个文件夹 folder[j] 下,那么 folder[i] 就…...
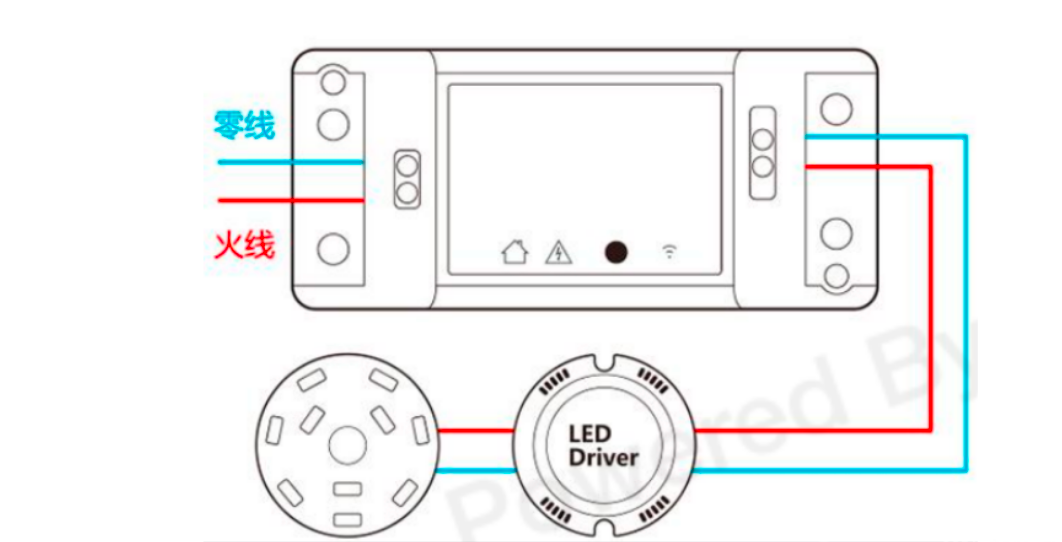
Homekit智能家居DIY设备-智能通断开关
智能通断器,也叫开关模块,可以非常方便地接入家中原有开关、插座、灯具、电器的线路中,通过手机App或者语音即可控制电路通断,轻松实现原有家居设备的智能化改造。 随着智能家居概念的普及,越来越多的人想将自己的家改…...
概述)
【java】EJB(Enterprise Java Bean)概述
EJB概述目录一、什么情况下需要企业Bean需要使用EJB的N个理由二、EJB的基本分类2.1、Enterprise Bean2.2、 Message Driven Bean(MDB)——消息驱动Bean,基于JMS三、定义客户端访问的接口3.1、 远程客户端——客户端与其调用的EJB对象不在同一个JVM进程中3.2、本地客户端——客户…...

Android 10.0 Launcher3桌面禁止左右滑动
1.1概述 在10.0的rom定制化开发中,由于Launcher3有一些功能需要定制,这样的需求也好多的,现在功能需求要求桌面固定在Launcher3的app列表页,不让左右移动,就是禁止左右移动的功能实现,所以需要禁止滑动分析页面滑动部分的功能,然后禁用 2.1Launcher3桌面禁止左右滑动的核…...

RestClient
什么是RestClient RestClient 是 Elasticsearch 官方提供的 Java 低级 REST 客户端,它允许HTTP与Elasticsearch 集群通信,而无需处理 JSON 序列化/反序列化等底层细节。它是 Elasticsearch Java API 客户端的基础。 RestClient 主要特点 轻量级ÿ…...

【Axure高保真原型】引导弹窗
今天和大家中分享引导弹窗的原型模板,载入页面后,会显示引导弹窗,适用于引导用户使用页面,点击完成后,会显示下一个引导弹窗,直至最后一个引导弹窗完成后进入首页。具体效果可以点击下方视频观看或打开下方…...

多云管理“拦路虎”:深入解析网络互联、身份同步与成本可视化的技术复杂度
一、引言:多云环境的技术复杂性本质 企业采用多云策略已从技术选型升维至生存刚需。当业务系统分散部署在多个云平台时,基础设施的技术债呈现指数级积累。网络连接、身份认证、成本管理这三大核心挑战相互嵌套:跨云网络构建数据…...

《从零掌握MIPI CSI-2: 协议精解与FPGA摄像头开发实战》-- CSI-2 协议详细解析 (一)
CSI-2 协议详细解析 (一) 1. CSI-2层定义(CSI-2 Layer Definitions) 分层结构 :CSI-2协议分为6层: 物理层(PHY Layer) : 定义电气特性、时钟机制和传输介质(导线&#…...

UDP(Echoserver)
网络命令 Ping 命令 检测网络是否连通 使用方法: ping -c 次数 网址ping -c 3 www.baidu.comnetstat 命令 netstat 是一个用来查看网络状态的重要工具. 语法:netstat [选项] 功能:查看网络状态 常用选项: n 拒绝显示别名&#…...

如何为服务器生成TLS证书
TLS(Transport Layer Security)证书是确保网络通信安全的重要手段,它通过加密技术保护传输的数据不被窃听和篡改。在服务器上配置TLS证书,可以使用户通过HTTPS协议安全地访问您的网站。本文将详细介绍如何在服务器上生成一个TLS证…...

PL0语法,分析器实现!
简介 PL/0 是一种简单的编程语言,通常用于教学编译原理。它的语法结构清晰,功能包括常量定义、变量声明、过程(子程序)定义以及基本的控制结构(如条件语句和循环语句)。 PL/0 语法规范 PL/0 是一种教学用的小型编程语言,由 Niklaus Wirth 设计,用于展示编译原理的核…...

Spring AI与Spring Modulith核心技术解析
Spring AI核心架构解析 Spring AI(https://spring.io/projects/spring-ai)作为Spring生态中的AI集成框架,其核心设计理念是通过模块化架构降低AI应用的开发复杂度。与Python生态中的LangChain/LlamaIndex等工具类似,但特别为多语…...

蓝桥杯 冶炼金属
原题目链接 🔧 冶炼金属转换率推测题解 📜 原题描述 小蓝有一个神奇的炉子用于将普通金属 O O O 冶炼成为一种特殊金属 X X X。这个炉子有一个属性叫转换率 V V V,是一个正整数,表示每 V V V 个普通金属 O O O 可以冶炼出 …...

作为测试我们应该关注redis哪些方面
1、功能测试 数据结构操作:验证字符串、列表、哈希、集合和有序的基本操作是否正确 持久化:测试aof和aof持久化机制,确保数据在开启后正确恢复。 事务:检查事务的原子性和回滚机制。 发布订阅:确保消息正确传递。 2、性…...
