数据结构时间空间复杂度笔记
🕺作者: 迷茫的启明星
本篇内容:数据结构时间空间复杂度笔记
😘欢迎关注:👍点赞🙌收藏✍️留言
🏇家人们,码字不易,你的👍点赞🙌收藏❤️关注对我真的很重要,有问题可在评论区提出,感谢阅读!!!
持续更新中~

文章目录
- 1.算法效率
- 1.1 如何衡量一个算法的好坏
- 1.2 算法的复杂度
- 1.3 复杂度在校招中的考察
- 2.时间复杂度
- 2.1 时间复杂度的概念
- 2.2 大O的渐进表示法
- 2.3常见时间复杂度计算举例
- 3.空间复杂度
- 4.常见时间复杂度
- 复杂度oj练习
1.算法效率
1.1 如何衡量一个算法的好坏
如何衡量一个算法的好坏呢?比如对于以下斐波那契数列:
long long Fib(int N) {if(N < 3)return 1;return Fib(N-1) + Fib(N-2); }斐波那契数列的递归实现方式非常简洁,但简洁一定好吗?那该如何衡量其好与坏呢?
1.2 算法的复杂度
算法在编写成可执行程序后,运行时需要耗费时间资源和空间(内存)资源 。因此衡量一个算法的好坏,一般是从时间和空间两个维度来衡量的,即时间复杂度和空间复杂度。
时间复杂度主要衡量一个算法的运行快慢,而空间复杂度主要衡量一个算法运行所需要的额外空间。在计算机发展的早期,计算机的存储容量很小。所以对空间复杂度很是在乎。但是经过计算机行业的迅速发展,计算机的存储容量已经达到了很高的程度。所以我们如今已经不需要再特别关注一个算法的空间复杂度。
1.3 复杂度在校招中的考察
2.时间复杂度
2.1 时间复杂度的概念
时间复杂度的定义:在计算机科学中,算法的时间复杂度是一个函数,它定量描述了该算法的运行时间。一个算法执行所耗费的时间,从理论上说,是不能算出来的,只有你把你的程序放在机器上跑起来,才能知
道。但是我们需要每个算法都上机测试吗?是可以都上机测试,但是这很麻烦,所以才有了时间复杂度这个分析方式。一个算法所花费的时间与其中语句的执行次数成正比例,算法中的基本操作的执行次数,为算法的时间复杂度。
即:找到某条基本语句与问题规模N之间的数学表达式,就是算出了该算法的时间复杂度。// 请计算一下Func1中++count语句总共执行了多少次? void Func1(int N) { int count = 0; for (int i = 0; i < N ; ++ i) { for (int j = 0; j < N ; ++ j) { ++count; } } for (int k = 0; k < 2 * N ; ++ k) { ++count; } int M = 10; while (M--) { ++count; } printf("%d\n", count); }Func1 执行的基本操作次数 :
- N = 10 F(N) = 130
- N = 100 F(N) = 10210
- N = 1000 F(N) = 1002010
实际中我们计算时间复杂度时,我们其实并不一定要计算精确的执行次数,而只需要大概执行次数,那么这
里我们使用大O的渐进表示法。
2.2 大O的渐进表示法
大O符号(Big O notation):是用于描述函数渐进行为的数学符号。
推导大O阶方法:
1、用常数1取代运行时间中的所有加法常数。
2、在修改后的运行次数函数中,只保留最高阶项。
3、如果最高阶项存在且不是1,则去除与这个项目相乘的常数。得到的结果就是大O阶。
使用大O的渐进表示法以后,Func1的时间复杂度为:O(N2)
- N = 10 F(N) = 100
- N = 100 F(N) = 10000
- N = 1000 F(N) = 1000000
通过上面我们会发现大O的渐进表示法去掉了那些对结果影响不大的项,简洁明了的表示出了执行次数。
另外有些算法的时间复杂度存在最好、平均和最坏情况:
最坏情况:任意输入规模的最大运行次数(上界)
平均情况:任意输入规模的期望运行次数
最好情况:任意输入规模的最小运行次数(下界)
例如:在一个长度为N数组中搜索一个数据x
最好情况:1次找到
最坏情况:N次找到
平均情况:N/2次找到
在实际中一般情况关注的是算法的最坏运行情况,所以数组中搜索数据时间复杂度为O(N)
2.3常见时间复杂度计算举例
实例1:
// 计算Func2的时间复杂度? void Func2(int N) {int count = 0;for (int k = 0; k < 2 * N ; ++ k){++count; }int M = 10;while (M--){++count;}printf("%d\n", count); }实例1基本操作执行了2N+10次
解析:第一个for循环次数为2N,第二个循环次数为10次
实例2:
// 计算Func3的时间复杂度? void Func3(int N, int M) {int count = 0;for (int k = 0; k < M; ++ k){++count;}for (int k = 0; k < N ; ++ k){++count;}printf("%d\n", count); }实例2基本操作执行了M+N次,有两个未知数M和N,时间复杂度为 O(N+M)
实例3:
// 计算Func4的时间复杂度? void Func4(int N) {int count = 0;for (int k = 0; k < 100; ++ k){++count;}printf("%d\n", count); }实例3基本操作执行了100次,通过推导大O阶方法,因为是常数项,时间复杂度为 O(1)
实例4:
// 计算strchr的时间复杂度? const char * strchr ( const char * str, int character );实例4基本操作执行最好1次,最坏N次,时间复杂度一般看最坏,时间复杂度为 O(N)
解析:strchr函数返回查找一个字符串中第一个出现character的位置的指针
实例5:
// 计算冒泡排序的时间复杂度? void BubbleSort(int* a, int n) {assert(a);for (size_t end = n; end > 0; --end){int exchange = 0;for (size_t i = 1; i < end; ++i){if (a[i-1] > a[i]){Swap(&a[i-1], &a[i]);exchange = 1;}}if (exchange == 0)break;} } //没有exchange就是最坏情况实例5基本操作执行最好N次,最坏执行了(N*(N+1)/2次,通过推导大O阶方法+时间复杂度一般看最坏,时间复杂度为 O(N^2)
实例6:
// 计算二分查找的时间复杂度? int BinarySearch(int* a, int n, int x) {assert(a);int begin = 0;int end = n-1;// [begin, end]:begin和end是左闭右闭区间,因此有=号while (begin <= end){int mid = begin + ((end-begin)>>1);if (a[mid] < x)begin = mid+1;else if (a[mid] > x)end = mid-1;elsereturn mid;}return -1; }实例6基本操作执行最好1次,最坏O(logN)次,时间复杂度为 O(logN) ps:logN在算法分析中表示是底数为2,对数为N。有些地方会写成lgN。
推导:
实例7:
// 计算阶乘递归Fac的时间复杂度? long long Fac(size_t N) { if(0 == N) return 1; return Fac(N-1)*N; }实例7通过计算分析发现基本操作递归了N次,时间复杂度为O(N)。
实例8:
// 计算斐波那契递归Fib的时间复杂度? long long Fib(size_t N) {if(N < 3)return 1;return Fib(N-1) + Fib(N-2); }实例8通过计算分析发现基本操作递归了2N次,时间复杂度为O(2N)。
3.空间复杂度
空间复杂度也是一个数学表达式,是对一个算法在运行过程中临时占用存储空间大小的量度 。
空间复杂度不是程序占用了多少bytes的空间,因为这个也没太大意义,所以空间复杂度算的是变量的个数。
空间复杂度计算规则基本跟实践复杂度类似,也使用大O渐进表示法。注意:函数运行时所需要的栈空间(存储参数、局部变量、一些寄存器信息等)在编译期间已经确定好了,因此空间复杂度主要通过函数在运行时候显式申请的额外空间来确定。
实例1:
// 计算BubbleSort的空间复杂度? void BubbleSort(int* a, int n) {assert(a);for (size_t end = n; end > 0; --end){int exchange = 0;for (size_t i = 1; i < end; ++i){if (a[i-1] > a[i]){Swap(&a[i-1], &a[i]);exchange = 1;}}if (exchange == 0)break;} }实例1中使用了常数个额外空间,所以空间复杂度为 O(1)
实例2:
// 计算Fibonacci的空间复杂度? // 返回斐波那契数列的前n项 long long* Fibonacci(size_t n) {if(n==0)return NULL;long long * fibArray = (long long *)malloc((n+1) * sizeof(long long));fibArray[0] = 0;fibArray[1] = 1;for (int i = 2; i <= n ; ++i){fibArray[i] = fibArray[i - 1] + fibArray [i - 2];}return fibArray; }实例2动态开辟了N个空间,空间复杂度为 O(N)
实例3:
// 计算阶乘递归Fac的空间复杂度? long long Fac(size_t N) {if(N == 0)return 1;return Fac(N-1)*N; }实例3递归调用了N次,开辟了N个栈帧,每个栈帧使用了常数个空间。空间复杂度为O(N)
4.常见时间复杂度
一般算法常见的复杂度如下:


复杂度oj练习
3.1消失的数字OJ链接:https://leetcode-cn.com/problems/missing-number-lcci/
int missingNumber(int* nums, int numsSize){int val=0;for(int i=0;i<numsSize;i++){val^=nums[i];}for(int i=0;i<numsSize+1;i++){val^=i;}return val;
}
使用异或的思想
3.2 旋转数组OJ链接:https://leetcode-cn.com/problems/rotate-array/

思路三:开辟新空间
void rotate(int* nums, int numsSize, int k){k=k%numsSize;int *c=(int *)malloc(sizeof(int)*numsSize);for(int i=0;i<k;i++){c[i]= nums[numsSize-k+i];}for(int i=k;i<numsSize;i++){c[i]=nums[i-k];}for(int i=0;i<numsSize;i++){nums[i]= c[i];}
}
相关文章:

数据结构时间空间复杂度笔记
🕺作者: 迷茫的启明星 本篇内容:数据结构时间空间复杂度笔记 😘欢迎关注:👍点赞🙌收藏✍️留言 🏇家人们,码字不易,你的👍点赞🙌收藏❤…...
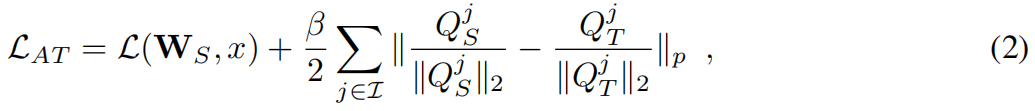
基于注意力的知识蒸馏Attention Transfer原理与代码解析
paper:Paying More Attention to Attention: Improving the Performance of Convolutional Neural Networks via Attention Transfercode:https://github.com/megvii-research/mdistiller/blob/master/mdistiller/distillers/AT.py背景一个流行的假设是存…...

利尔达在北交所上市:总市值突破29亿元,叶文光为董事长
2月17日,利尔达科技集团股份有限公司(下称“利尔达”,BJ:832149)在北京证券交易所上市。本次上市,利尔达的发行价格为5.00元/股,发行数量为1980万股,发行市盈率为12.29倍,募资总额为…...
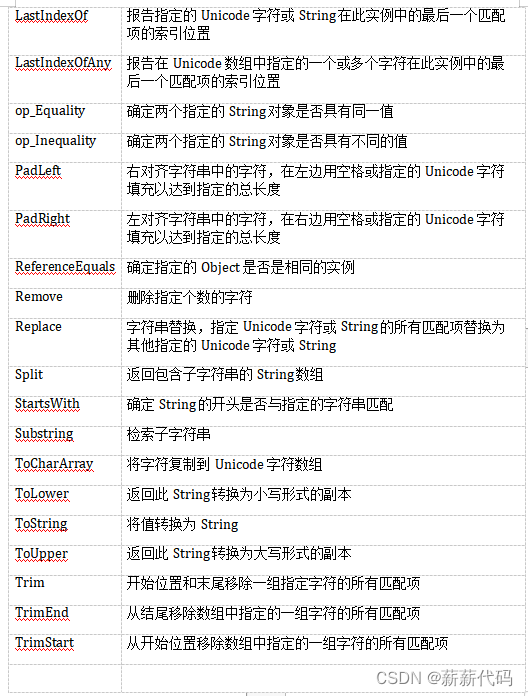
C#操作字符串方法 [万余字总结 · 详细]
C#操作字符串方法总结C#常用字符串函数大全C#常用字符串操作方法C#操作字符串方法总结C#常用字符串函数大全 Compare 比较字符串的内容,考虑文化背景(场所),确定某些字符是否相等 CompareOrdinal 与Compare一样,但不考虑文化背景 Format 格…...

极兔一面:10亿级ES海量搜索狂飙10倍,该怎么办?
背景说明: ES高性能全文索引,如果不会用,或者没有用过,在面试中,会非常吃亏。 所以ES的实操和底层原理,大家要好好准备。 另外,ES调优是一个非常、非常核心的面试知识点,大家要非…...
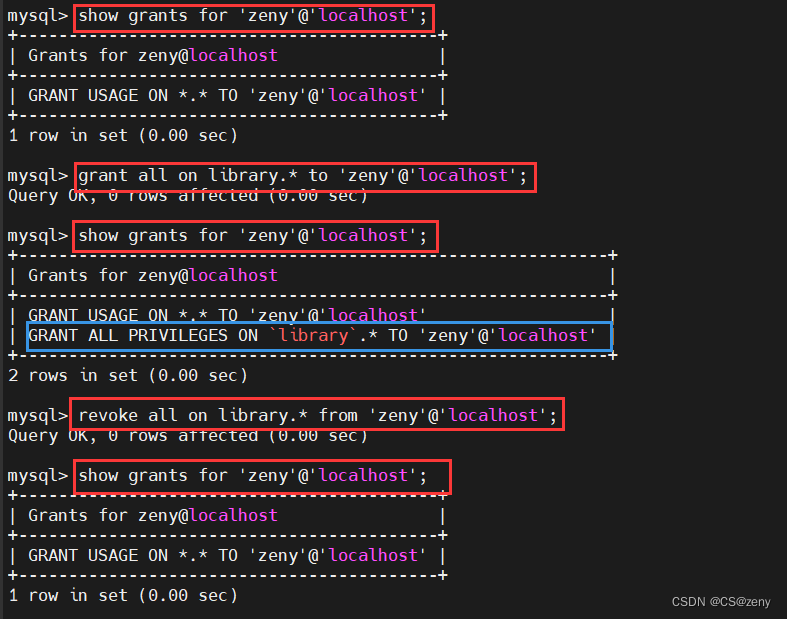
【Mysql基础 —— SQL语句(一)】
文章目录概述使用启动/停止mysql服务连接mysql客户端数据模型SQLSQL语句分类DDL数据库操作表操作查询创建数据类型修改删除DML添加数据修改数据删除数据DQL基础查询条件查询聚合函数分组查询排序查询分页查询执行顺序DCL管理用户权限控制概述 数据库(Database&#…...
 | 机试题算法思路)
华为OD机试 - 新员工座位安排系统(Python) | 机试题算法思路
最近更新的博客 华为OD机试 - 招聘(Python) | 备考思路,刷题要点,答疑 【新解法】华为OD机试 - 五键键盘 | 备考思路,刷题要点,答疑 【新解法】华为OD机试 - 热点网络统计 | 备考思路,刷题要点,答疑 【新解法】华为OD机试 - 路灯照明 | 备考思路,刷题要点,答疑 【新解…...

MySQL - 介绍
前言 本篇介绍认识MySQL,重装mysql操作 如有错误,请在评论区指正,让我们一起交流,共同进步! 本文开始 1.什么是数据库? 数据库: 一种通过SQL语言操作管理数据的软件; 重装数据库的卸载数据库步骤 : ① 停止MySQL服…...

ChatGPT国内镜像站初体验:聊天、Python代码生成等
ChatGPT国内镜像站初体验,聊天、Python代码生成。 (本文获得CSDN质量评分【92】)【学习的细节是欢悦的历程】Python 官网:https://www.python.org/ Free:大咖免费“圣经”教程《 python 完全自学教程》,不仅仅是基础那么简单………...
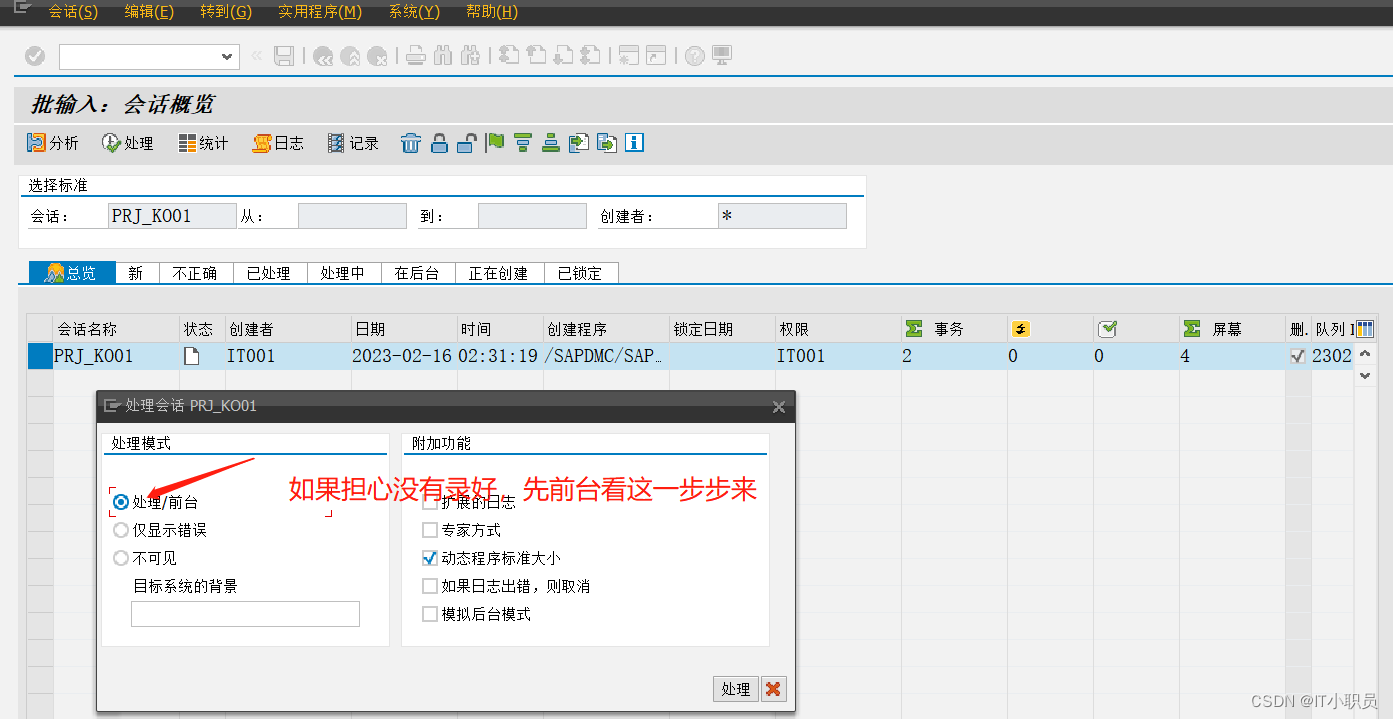
SAP数据导入工具(LSMW) 超级详细教程(批量导入内部订单)
目录 第一步:记录批导步骤编辑数据源对应字段 第二步:维护数据源 第三步:维护数据源对应字段(重要) 第四步:维护数据源关系。 第五步:维护数据源与导入字段的对应关系。 第六步࿰…...
第9天-商品服务(电商核心概念,属性分组开发及分类和品牌的级联更新)
1.电商核心概念 1.1.SPU与SKU SPU:Standard Product Unit(标准化产品单元) 是商品信息聚合的最小单位,是一组可复用、易检索的标准化信息的集合,该集合描述了一个 产品的特性。 决定商品属性的值 SKU:Stock…...

动漫人物眼睛画法
本期的动漫绘画课程教大家来学习动漫人物眼睛画法,结合板绘软件从草稿开始一步步教你画出动漫人物眼睛,不用报动漫培训班也能学会,快来跟着本期的动漫人物眼睛画法教程试试吧! 动漫人物眼睛画法步骤教程: 注意&#x…...

张晨光-JAVA零基础保姆式JDBC技术教程
JDBC文档 JDBC概述 JDBC概述 Java DataBase Connectivity Java 数据库连接技术 JDBC的作用 通过Java语言操作数据库,操作表中的数据 SUN公司为**了简化、**统一对数据库的操作,定义了一套Java操作数据库的规范,称之为JDBC JDBC的本质 是官方…...
)
华为OD机试 - 最多提取子串数目(Python)
最多提取子串数目 题目 给定由 [a-z] 26 个英文小写字母组成的字符串 A 和 B,其中 A 中可能存在重复字母,B 中不会存在重复字母 现从字符串 A 中按规则挑选一些字母,可以组成字符串 B。 挑选规则如下: 1) 同一个位置的字母只能被挑选一次 2) 被挑选字母的相对先后顺序不…...

LeetCode-1237. 找出给定方程的正整数解【双指针,二分查找】
LeetCode-1237. 找出给定方程的正整数解【双指针,二分查找】题目描述:解题思路一:双指针。首先我们不管f是什么,即function_id等于什么不管。但是我们可以调用customfunction中的f函数,然后我们遍历x,y(1 < x, y &l…...

广度优先搜索算法 - 迷宫找路
广度优先搜索算法1 思考问题1.1 这个迷宫需不需要指定入口和出口?2 先粗略实现2.1 源码2.2 源码解释3 优化代码3.1 优化读取文件部分3.2 增加错误处理4 再优化-让程序变得更加灵活4.1 用户外部可以循环输入入口和出口5 完整代码这是一个提问者的提出的问题ÿ…...

泡脚材料简记
文章目录一般条件中药包(药粉)泡脚丸中药包(药材)艾叶生姜益母草藏红花食盐花椒白醋柠檬藿香泡脚私方紫苏叶、白术、白芍、黄芪、青皮、柴胡、夜交藤、丹参、当归,每种各10g艾叶、花椒、肉桂、桂枝、红花干姜30克、小茴…...
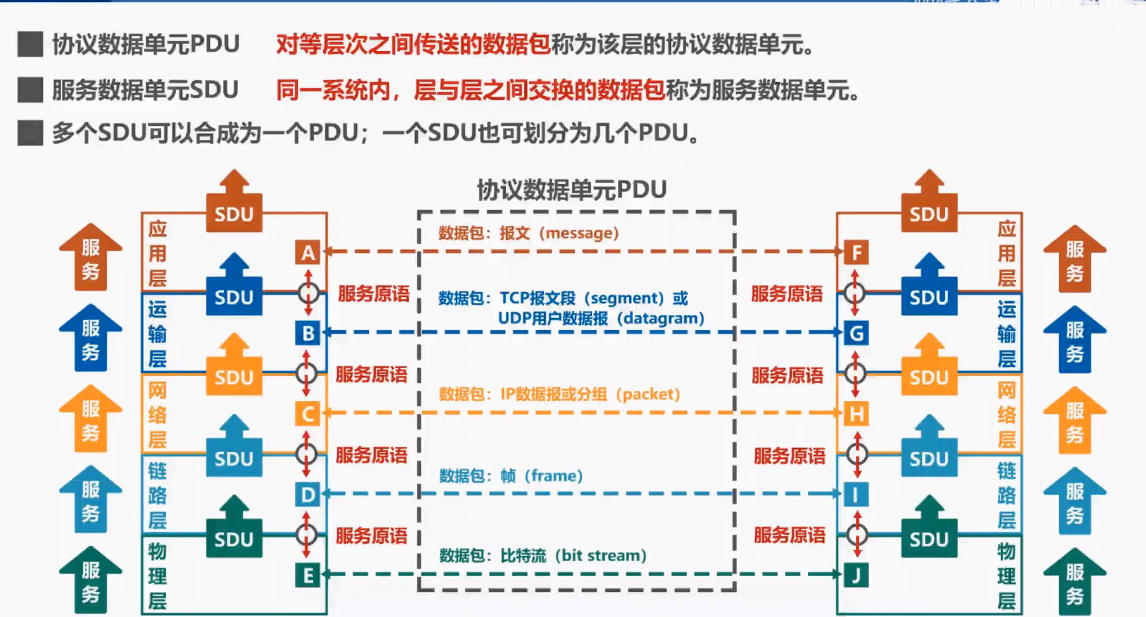
【计算机网络】因特网概述
文章目录因特网概述网络、互联网和因特网互联网历史与ISP标准化与RFC因特网的组成三种交换方式电路交换分组交换和报文交换三种交换方式的对比与总结计算机网络的定义和分类计算机网络的定义计算机网络的分类计算机网络的性能指标速率带宽吞吐量时延时延带宽积往返时间利用率丢…...

STC单片机 VS/HX1838红外接收和发送实验
STC单片机 VS/HX1838红外接收和发送实验 📌相关篇《STC单片机获取红外解码从串口输出》🔨所使用的红外接收头VS1838 📋VS1838引脚定义🌿5MM发射头,940nm红外发射二极管 红外遥控发射头。(外观看起来和普通的发光二极管没有什么差异,购买时需要注意确认)。 🔰采用的…...

前端开发常用案例(一)
前端开发常用案例1.实现三角形百度热榜样式分页效果小米商城自动轮播图效果二级下拉菜单效果时间轴效果展示音乐排行榜效果鼠标移入文字加载动画鼠标悬停缩放效果1.实现三角形 <!DOCTYPE html> <html lang"en"> <head><meta charset"UTF-8…...

XML Group端口详解
在XML数据映射过程中,经常需要对数据进行分组聚合操作。例如,当处理包含多个物料明细的XML文件时,可能需要将相同物料号的明细归为一组,或对相同物料号的数量进行求和计算。传统实现方式通常需要编写脚本代码,增加了开…...

【第二十一章 SDIO接口(SDIO)】
第二十一章 SDIO接口 目录 第二十一章 SDIO接口(SDIO) 1 SDIO 主要功能 2 SDIO 总线拓扑 3 SDIO 功能描述 3.1 SDIO 适配器 3.2 SDIOAHB 接口 4 卡功能描述 4.1 卡识别模式 4.2 卡复位 4.3 操作电压范围确认 4.4 卡识别过程 4.5 写数据块 4.6 读数据块 4.7 数据流…...

条件运算符
C中的三目运算符(也称条件运算符,英文:ternary operator)是一种简洁的条件选择语句,语法如下: 条件表达式 ? 表达式1 : 表达式2• 如果“条件表达式”为true,则整个表达式的结果为“表达式1”…...

Java-41 深入浅出 Spring - 声明式事务的支持 事务配置 XML模式 XML+注解模式
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

相机从app启动流程
一、流程框架图 二、具体流程分析 1、得到cameralist和对应的静态信息 目录如下: 重点代码分析: 启动相机前,先要通过getCameraIdList获取camera的个数以及id,然后可以通过getCameraCharacteristics获取对应id camera的capabilities(静态信息)进行一些openCamera前的…...

Unit 1 深度强化学习简介
Deep RL Course ——Unit 1 Introduction 从理论和实践层面深入学习深度强化学习。学会使用知名的深度强化学习库,例如 Stable Baselines3、RL Baselines3 Zoo、Sample Factory 和 CleanRL。在独特的环境中训练智能体,比如 SnowballFight、Huggy the Do…...

【碎碎念】宝可梦 Mesh GO : 基于MESH网络的口袋妖怪 宝可梦GO游戏自组网系统
目录 游戏说明《宝可梦 Mesh GO》 —— 局域宝可梦探索Pokmon GO 类游戏核心理念应用场景Mesh 特性 宝可梦玩法融合设计游戏构想要素1. 地图探索(基于物理空间 广播范围)2. 野生宝可梦生成与广播3. 对战系统4. 道具与通信5. 延伸玩法 安全性设计 技术选…...

sipsak:SIP瑞士军刀!全参数详细教程!Kali Linux教程!
简介 sipsak 是一个面向会话初始协议 (SIP) 应用程序开发人员和管理员的小型命令行工具。它可以用于对 SIP 应用程序和设备进行一些简单的测试。 sipsak 是一款 SIP 压力和诊断实用程序。它通过 sip-uri 向服务器发送 SIP 请求,并检查收到的响应。它以以下模式之一…...

【网络安全】开源系统getshell漏洞挖掘
审计过程: 在入口文件admin/index.php中: 用户可以通过m,c,a等参数控制加载的文件和方法,在app/system/entrance.php中存在重点代码: 当M_TYPE system并且M_MODULE include时,会设置常量PATH_OWN_FILE为PATH_APP.M_T…...

【Linux手册】探秘系统世界:从用户交互到硬件底层的全链路工作之旅
目录 前言 操作系统与驱动程序 是什么,为什么 怎么做 system call 用户操作接口 总结 前言 日常生活中,我们在使用电子设备时,我们所输入执行的每一条指令最终大多都会作用到硬件上,比如下载一款软件最终会下载到硬盘上&am…...





