机器学习笔记之优化算法(十一)凸函数铺垫:梯度与方向导数
机器学习笔记之优化算法——凸函数铺垫:梯度与方向导数
- 引言
- 回顾:偏导数
- 方向余弦
- 方向导数
- 方向导数的几何意义
- 方向导数的定义
- 方向导数与偏导数之间的关联关系
- 证明过程
- 梯度 ( Gradient ) (\text{Gradient}) (Gradient)
引言
本节作为介绍凸函数的铺垫,简单介绍方向导数与梯度。
回顾:偏导数
以二元函数 f ( x , y ) f(x,y) f(x,y)为例,其关于变量的偏导数表示:三维空间中,曲面上某一点沿着 x x x轴方向或 y y y轴方向变化的速率。也就是说:
在梯度下降法——铺垫中解释过,下图中描述斜率的红色切线不是方向;真正描述方向的是红色箭头。
- ∂ f ( x , y ) ∂ x = f x ( x , y ) \begin{aligned}\frac{\partial f(x,y)}{\partial x} = f_x(x,y)\end{aligned} ∂x∂f(x,y)=fx(x,y)表示函数 f ( x , y ) f(x,y) f(x,y)沿着 x x x轴方向的斜率;
下图中P \mathcal P P点沿着 x x x轴方向的红色直线所描述的斜率; - 同理, ∂ f ( x , y ) ∂ y = f y ( x , y ) \begin{aligned}\frac{\partial f(x,y)}{\partial y} = f_y(x,y)\end{aligned} ∂y∂f(x,y)=fy(x,y)表示函数 f ( x , y ) f(x,y) f(x,y)沿着 y y y轴方向的斜率。
下图中P \mathcal P P点沿着 y y y轴方向的红色直线所描述的斜率。

f ( x , y ) f(x,y) f(x,y)在点 P ( x 0 , y 0 ) \mathcal P(x_0,y_0) P(x0,y0)关于 x , y x,y x,y的偏导数分别表示如下:
第一个公式即: y = y 0 y=y_0 y=y0不变,观察变量 x x x的斜率; x x x同理。
{ f x ( x 0 , y 0 ) = lim Δ x ⇒ 0 f ( x 0 + Δ x , y 0 ) − f ( x 0 , y 0 ) Δ x f y ( x 0 , y 0 ) = lim Δ y ⇒ 0 f ( x 0 , y + Δ y ) − f ( x 0 , y 0 ) Δ y \begin{cases} \begin{aligned} & f_x(x_0,y_0) = \mathop{\lim}\limits_{\Delta x \Rightarrow 0} \frac{f(x_0 + \Delta x,y_0) - f(x_0,y_0)}{\Delta x} \\ & f_y(x_0,y_0) = \mathop{\lim}\limits_{\Delta y \Rightarrow 0} \frac{f(x_0,y+\Delta y) - f(x_0,y_0)}{\Delta y} \end{aligned} \end{cases} ⎩ ⎨ ⎧fx(x0,y0)=Δx⇒0limΔxf(x0+Δx,y0)−f(x0,y0)fy(x0,y0)=Δy⇒0limΔyf(x0,y+Δy)−f(x0,y0)
观察上图中的 P \mathcal P P点,它仅仅在 x , y x,y x,y两个方向(红色箭头)上有导数吗 ? ? ?并不是,在其他方向同样可以存在导数。由此,引出方向导数 ( Directional Derivative ) (\text{Directional Derivative}) (Directional Derivative)的概念。
例如下图中 P \mathcal P P点,其导数方向可以有很多。例如黄色箭头描述的方向。

方向余弦
关于某向量 l ⃗ \vec l l在坐标系中表示如下:

在坐标系中记作 l ⃗ = ( a , b ) \vec l =(a,b) l=(a,b);如果要将 l ⃗ \vec l l单位化,得到单位向量 l ⃗ o \vec l^{o} lo,则执行:
l ⃗ o = 1 a 2 + b 2 ( a , b ) = ( a a 2 + b 2 , b a 2 + b 2 ) \begin{aligned} \vec l^{o} & = \frac{1}{\sqrt{a^2 + b^2}} (a,b) \\ & = \left(\frac{a}{\sqrt{a^2 + b^2}},\frac{b}{\sqrt{a^2 + b^2}}\right) \end{aligned} lo=a2+b21(a,b)=(a2+b2a,a2+b2b)
观察上图,可以将 a a 2 + b 2 = cos α , b a 2 + b 2 = sin α = cos β \begin{aligned}\frac{a}{\sqrt{a^2 + b^2}} = \cos \alpha,\frac{b}{\sqrt{a^2 + b^2}} = \sin \alpha = \cos \beta\end{aligned} a2+b2a=cosα,a2+b2b=sinα=cosβ,最终 l ⃗ o \vec l^{o} lo可表示为: ( cos α , cos β ) (\cos \alpha,\cos \beta) (cosα,cosβ)
也就是说,单位向量可以表示成这种方向余弦的形式。
方向导数
方向导数的几何意义
依然以上述图形示例:可能存在各种各样(黄色箭头)的方向,这里以黄色直线箭头为例,该方向的在函数图像中的投影会呈现一条轨迹(黄色实线):
实际上这条轨迹就是过 P \mathcal P P点,在该方向朝向的、与坐标平面 X O Y \mathcal X\mathcal O\mathcal Y XOY垂直的平面把 f ( x , y ) f(x,y) f(x,y)截断产生的图像

去掉其他多余的箭头,过 P ( x 0 , y 0 ) \mathcal P(x_0,y_0) P(x0,y0)对应的函数结果位置做一条切线,而切线的斜率即函数在 P \mathcal P P点处的斜率(黑色直线):
其中黄色菱形表示截断平面中间由实线与虚线组成的类似梯形的区域表示截面,只不过虚线部分的轨迹并不是当前方向对应的轨迹,不是我们我们关注的对象。

由此可见:在 P \mathcal P P点的 36 0 o 360^o 360o方向上,每一个方向都存在一个截面,随着方向的变化,对应的函数结果 f ( x 0 , y 0 ) f(x_0,y_0) f(x0,y0)在截面上的位置得到不同的切线(斜率)结果。
准确来说是截线而不是截面,因为函数 f ( ⋅ ) f(\cdot) f(⋅)是空心的。
方向导数的定义
如何定义方向导数 ? ? ?见下图:

上述图像描述 X O Y \mathcal X\mathcal O\mathcal Y XOY平面上, P ( x 0 , y 0 ) \mathcal P(x_0,y_0) P(x0,y0)点沿着 l ⃗ \vec l l方向前进了一个极小的长度 t t t并到达 A \mathcal A A点,对应 P \mathcal P P在函数上的映射结果 z 0 = f ( x 0 , y 0 ) z_0= f(x_0,y_0) z0=f(x0,y0)也会沿着对应的轨迹移动一个距离,并达到新的位置 z 0 ′ z_0' z0′;假设 Δ Z = ∣ z 0 − z 0 ′ ∣ \Delta \mathcal Z = |z_0 - z_0'| ΔZ=∣z0−z0′∣,对应的方向导数可表示为:
lim t ⇒ 0 Δ Z t \mathop{\lim}\limits_{t \Rightarrow 0} \frac{\Delta \mathcal Z}{t} t⇒0limtΔZ
已知 P \mathcal P P点坐标是 ( x 0 , y 0 ) (x_0,y_0) (x0,y0),并且已知距离 t t t以及对应的 α , β \alpha,\beta α,β夹角,因而可以得到 A \mathcal A A的坐标: A ( x 0 + t ⋅ cos α , y 0 + t ⋅ cos β ) \mathcal A (x_0 + t \cdot \cos \alpha,y_0 + t \cdot \cos \beta) A(x0+t⋅cosα,y0+t⋅cosβ)。最终可以将 ( x 0 , y 0 ) (x_0,y_0) (x0,y0)处关于向量 l ⃗ \vec l l的方向导数 ∂ Z ∂ l ⃗ ∣ ( x 0 , y 0 ) \begin{aligned}\frac{\partial \mathcal Z}{\partial {\vec l}}|_{(x_0,y_0)}\end{aligned} ∂l∂Z∣(x0,y0)表达为如下形式:
∂ Z ∂ l ⃗ ∣ ( x 0 , y 0 ) = lim t ⇒ 0 f ( x 0 + t ⋅ cos α , y 0 + t ⋅ cos β ) − f ( x 0 , y 0 ) t \frac{\partial \mathcal Z}{\partial {\vec l}}|_{(x_0,y_0)} = \mathop{\lim}\limits_{t \Rightarrow 0} \frac{f(x_0 + t \cdot \cos \alpha,y_0 + t \cdot \cos \beta) - f(x_0,y_0)}{t} ∂l∂Z∣(x0,y0)=t⇒0limtf(x0+t⋅cosα,y0+t⋅cosβ)−f(x0,y0)
基于方向导数重新观察偏导数,可以发现:方向导数就是偏导数的一种特例。以 ∂ f ( x , y ) ∂ x \begin{aligned}\frac{\partial f(x,y)}{\partial x}\end{aligned} ∂x∂f(x,y)为例。它等价于: l ⃗ \vec l l的方向是 x x x轴的正方向:

此时: α = 0 , β = π 2 ⇒ cos α = 1 , cos β = 0 \begin{aligned}\alpha = 0,\beta = \frac{\pi}{2} \Rightarrow \cos \alpha = 1,\cos \beta = 0\end{aligned} α=0,β=2π⇒cosα=1,cosβ=0从而有:
此时的方向导数退化成了偏导数, ∂ f ( x , y ) ∂ y \begin{aligned}\frac{\partial f(x,y)}{\partial y}\end{aligned} ∂y∂f(x,y)同理,这里不再赘述。
∂ Z ∂ l ⃗ = lim t ⇒ 0 f ( x 0 + t , y 0 ) − f ( x 0 , y 0 ) t = f x ( x 0 , y 0 ) = ∂ f ( x , y ) ∂ x ∣ ( x 0 , y 0 ) \begin{aligned} \frac{\partial \mathcal Z}{\partial \vec l} = \mathop{\lim}\limits_{t \Rightarrow 0} \frac{f(x_0 + t,y_0) - f(x_0,y_0)}{t} = f_x(x_0,y_0) = \frac{\partial f(x,y)}{\partial x}|_{(x_0,y_0)} \end{aligned} ∂l∂Z=t⇒0limtf(x0+t,y0)−f(x0,y0)=fx(x0,y0)=∂x∂f(x,y)∣(x0,y0)
方向导数与偏导数之间的关联关系
在函数 f ( ⋅ ) f(\cdot) f(⋅)在其定义域内可微的条件下,该函数在 ( x 0 , y 0 ) (x_0,y_0) (x0,y0)处关于方向向量 l ⃗ \vec l l的方向导数 ∂ Z ∂ l ⃗ ∣ ( x 0 , y 0 ) \begin{aligned}\frac{\partial \mathcal Z}{\partial {\vec l}}|_{(x_0,y_0)}\end{aligned} ∂l∂Z∣(x0,y0)与该函数在 ( x 0 , y 0 ) (x_0,y_0) (x0,y0)处的偏导数 f x ( x 0 , y 0 ) , f y ( x 0 , y 0 ) f_x(x_0,y_0),f_y(x_0,y_0) fx(x0,y0),fy(x0,y0)之间的关联关系表示如下:
∂ Z ∂ l ⃗ ∣ ( x 0 , y 0 ) = f x ( x 0 , y 0 ) ⋅ cos α + f y ( x 0 , y 0 ) ⋅ cos β \begin{aligned}\frac{\partial \mathcal Z}{\partial {\vec l}}|_{(x_0,y_0)} = f_x(x_0,y_0) \cdot \cos \alpha + f_y(x_0,y_0) \cdot \cos \beta\end{aligned} ∂l∂Z∣(x0,y0)=fx(x0,y0)⋅cosα+fy(x0,y0)⋅cosβ
证明过程
- 在函数 f ( ⋅ ) f(\cdot) f(⋅)可微的条件下,在 ( x 0 , y 0 ) (x_0,y_0) (x0,y0)点关于 Z \mathcal Z Z的变化量 Δ Z \Delta \mathcal Z ΔZ可表示为:
其中O [ ( Δ x ) 2 + ( Δ y ) 2 ] \mathcal O\left[\sqrt{({\Delta x})^2 + (\Delta y)^2}\right] O[(Δx)2+(Δy)2]表示关于( Δ x ) 2 + ( Δ y ) 2 \sqrt{({\Delta x})^2 + (\Delta y)^2} (Δx)2+(Δy)2的高阶无穷小。
Δ Z = f x ( x 0 , y 0 ) ⋅ Δ x + f y ( x 0 , y 0 ) ⋅ Δ y + O [ ( Δ x ) 2 + ( Δ y ) 2 ] \Delta \mathcal Z = f_x(x_0,y_0) \cdot \Delta x + f_y(x_0,y_0) \cdot \Delta y + \mathcal O\left[\sqrt{({\Delta x})^2 + (\Delta y)^2}\right] ΔZ=fx(x0,y0)⋅Δx+fy(x0,y0)⋅Δy+O[(Δx)2+(Δy)2] - 由于全微分在任意方向上均成立。

因而有:
{ Δ x = t ⋅ cos α Δ y = t ⋅ cos β ( Δ x ) 2 + ( Δ y ) 2 = t 2 ⋅ ( cos 2 α + cos 2 β ) = t 2 α + β = π 2 \begin{cases} \begin{aligned} & \Delta x = t \cdot \cos \alpha \\ & \Delta y = t \cdot \cos \beta \\ & (\Delta x)^2 + (\Delta y)^2 = t^2 \cdot (\cos^2 \alpha + \cos^2 \beta) = t^2 \quad \alpha +\beta = \frac{\pi}{2} \end{aligned} \end{cases} ⎩ ⎨ ⎧Δx=t⋅cosαΔy=t⋅cosβ(Δx)2+(Δy)2=t2⋅(cos2α+cos2β)=t2α+β=2π - 观察等式左侧:
Δ Z \Delta \mathcal Z ΔZ表示P ( x 0 , y 0 ) \mathcal P(x_0,y_0) P(x0,y0)沿着l ⃗ \vec l l移动t t t到达A \mathcal A A点前后函数结果的变化量。
I left = Δ Z = f ( x 0 + t ⋅ cos α , y 0 + t ⋅ cos β ) − f ( x 0 , y 0 ) \mathcal I_{\text{left}} = \Delta \mathcal Z = f(x_0 + t \cdot \cos \alpha,y_0 + t \cdot \cos \beta) - f(x_0,y_0) Ileft=ΔZ=f(x0+t⋅cosα,y0+t⋅cosβ)−f(x0,y0)
观察等式右侧:
将上述公式代入。
I right = f x ( x 0 , y 0 ) ⋅ t ⋅ cos α + f y ( x 0 , y 0 ) ⋅ t ⋅ cos β + O ( t ) \mathcal I_{\text{right}} = f_x(x_0,y_0) \cdot t \cdot \cos \alpha + f_y(x_0,y_0) \cdot t \cdot \cos \beta + \mathcal O(t) Iright=fx(x0,y0)⋅t⋅cosα+fy(x0,y0)⋅t⋅cosβ+O(t) - 将 I left , I right \mathcal I_{\text{left}},\mathcal I_{\text{right}} Ileft,Iright同时除以 t t t,等式两端依然相等:
并令I left \mathcal I_{\text{left}} Ileft中t ⇒ 0 t \Rightarrow 0 t⇒0,因为I Right \mathcal I_{\text{Right}} IRight中不含t ( O ( t ) t = 0 ) t \left(\begin{aligned}\frac{\mathcal O(t)}{t} = 0\end{aligned} \right) t(tO(t)=0),因此不产生影响。
{ I right t = f x ( x 0 , y 0 ) ⋅ cos α ⋅ t + f y ( x 0 , y 0 ) ⋅ cos β ⋅ t + O ( t ) t = f x ( x 0 , y 0 ) ⋅ cos α + f y ( x 0 , y 0 ) ⋅ cos β lim t ⇒ 0 I l e f t t = lim t ⇒ 0 f ( x 0 + t ⋅ cos α , y 0 + t ⋅ cos β ) − f ( x 0 , y 0 ) t = ∂ Z ∂ l ⃗ ∣ ( x 0 , y 0 ) \begin{cases} \begin{aligned} \frac{\mathcal I_{\text{right}}}{t} & = \frac{f_x(x_0,y_0) \cdot \cos \alpha \cdot t + f_y(x_0,y_0) \cdot \cos \beta \cdot t + \mathcal O(t)}{t} \\ & = f_x(x_0,y_0) \cdot \cos \alpha + f_y(x_0,y_0) \cdot \cos \beta \\ \mathop{\lim}\limits_{t \Rightarrow 0} \frac{\mathcal I_{left}}{t} & = \mathop{\lim}\limits_{t \Rightarrow 0} \frac{f(x_0 + t \cdot \cos \alpha,y_0 + t \cdot \cos \beta) - f(x_0,y_0)}{t} \\ & = \frac{\partial \mathcal Z}{\partial \vec l}|_{(x_0,y_0)} \end{aligned} \end{cases} ⎩ ⎨ ⎧tIrightt⇒0limtIleft=tfx(x0,y0)⋅cosα⋅t+fy(x0,y0)⋅cosβ⋅t+O(t)=fx(x0,y0)⋅cosα+fy(x0,y0)⋅cosβ=t⇒0limtf(x0+t⋅cosα,y0+t⋅cosβ)−f(x0,y0)=∂l∂Z∣(x0,y0) - 最终有:
∂ Z ∂ l ⃗ ∣ ( x 0 , y 0 ) = f x ( x 0 , y 0 ) ⋅ cos α + f y ( x 0 , y 0 ) ⋅ cos β \frac{\partial \mathcal Z}{\partial \vec l}|_{(x_0,y_0)} = f_x(x_0,y_0) \cdot \cos \alpha + f_y(x_0,y_0) \cdot \cos \beta ∂l∂Z∣(x0,y0)=fx(x0,y0)⋅cosα+fy(x0,y0)⋅cosβ
证毕。
梯度 ( Gradient ) (\text{Gradient}) (Gradient)
关于梯度,它的返回结果是一个向量形式。关于函数 f ( x , y ) f(x,y) f(x,y),其梯度向量通常记作: grad f ( x , y ) \text{grad } f(x,y) grad f(x,y)或者 ∇ f ( x , y ) \nabla f(x,y) ∇f(x,y)。
其具体表示为:
∇ f ( x , y ) = [ f x ( x , y ) , f y ( x , y ) ] \nabla f(x,y) = \left[f_x(x,y),f_y(x,y)\right] ∇f(x,y)=[fx(x,y),fy(x,y)]
很明显:梯度向量中的元素就是 f ( x , y ) f(x,y) f(x,y)针对不同自变量 x , y x,y x,y的偏导数。因此它的计算并不麻烦,如何理解梯度向量 ? ? ?具体从方向和大小两个角度对梯度向量进行认知。
回顾上面的方向导数 ∂ Z ∂ l ⃗ \begin{aligned}\frac{\partial \mathcal Z}{\partial \vec l}\end{aligned} ∂l∂Z,它可以表示成如下形式:
两向量之间的内积形式。- l ⃗ o \vec l^{o} lo
是l ⃗ \vec l l的单位向量结果。
∂ Z ∂ l ⃗ = f x ( x , y ) ⋅ cos α + f y ( x , y ) ⋅ cos β = [ f x ( x , y ) , f y ( x , y ) ] ( cos α cos β ) = ∇ f ( x , y ) ⋅ l ⃗ o \begin{aligned} \frac{\partial \mathcal Z}{\partial \vec l} & = f_x(x,y) \cdot \cos \alpha + f_y(x,y) \cdot \cos \beta \\ & = \left[f_x(x,y),f_y(x,y)\right] \begin{pmatrix} \cos \alpha \\ \cos \beta \end{pmatrix} \\ & = \nabla f(x,y) \cdot \vec l^{o} \end{aligned} ∂l∂Z=fx(x,y)⋅cosα+fy(x,y)⋅cosβ=[fx(x,y),fy(x,y)](cosαcosβ)=∇f(x,y)⋅lo
首先,由于 x , y x,y x,y轴描述的方向是确定的,因而在某点 ( x , y ) (x,y) (x,y)处的梯度向量也同样是固定的;但 l ⃗ o \vec l^{o} lo却不固定。由于是内积结果,我们可以将其展开:
∂ Z ∂ l ⃗ = ∇ f ( x , y ) ⋅ l ⃗ o = ∣ ∣ ∇ f ( x , y ) ∣ ∣ ⋅ ∣ ∣ l ⃗ o ∣ ∣ ⋅ cos θ \begin{aligned}\frac{\partial \mathcal Z}{\partial \vec l} & = \nabla f(x,y) \cdot \vec l^{o} \\ & = ||\nabla f(x,y)|| \cdot ||\vec l^{o}|| \cdot \cos \theta \end{aligned} ∂l∂Z=∇f(x,y)⋅lo=∣∣∇f(x,y)∣∣⋅∣∣lo∣∣⋅cosθ
观察:由于 ∣ ∣ ∇ f ( x , y ) ∣ ∣ = [ f x ( x , y ) ] 2 + [ f y ( x , y ) ] 2 ||\nabla f(x,y)|| = [f_x(x,y)]^2 + [f_y(x,y)]^2 ∣∣∇f(x,y)∣∣=[fx(x,y)]2+[fy(x,y)]2,因而在函数 f ( ⋅ ) f(\cdot) f(⋅)某一点 ( x , y ) (x,y) (x,y)确定的条件下,其值也是固定的;并且 ∣ ∣ l ⃗ o ∣ ∣ = 1 ||\vec l^{o}|| = 1 ∣∣lo∣∣=1。因此:影响 ∂ Z ∂ l ⃗ \begin{aligned}\frac{\partial \mathcal Z}{\partial \vec l}\end{aligned} ∂l∂Z大小的因素只有向量 ∇ f ( x , y ) \nabla f(x,y) ∇f(x,y)与向量 l ⃗ o \vec l^{o} lo之间的夹角 cos θ \cos \theta cosθ。
由于 cos θ ∈ [ − 1 , 1 ] \cos \theta \in [-1,1] cosθ∈[−1,1],因此当 θ = 0 \theta = 0 θ=0时,也就是 l ⃗ o \vec l^{o} lo与 ∇ f ( x , y ) \nabla f(x,y) ∇f(x,y)方向重合时,方向导数取得最大值,最大值即:
∂ Z ∂ l ⃗ = ∣ ∣ ∇ f ( x , y ) ∣ ∣ \frac{\partial \mathcal Z}{\partial \vec l} = ||\nabla f(x,y)|| ∂l∂Z=∣∣∇f(x,y)∣∣
也就是说:当前点 ( x , y ) (x,y) (x,y),选择梯度方向时,它的斜率(变化量)最大。
相关参考:
【多元微分专题】第六期:方向导数和梯度的直观理解
相关文章:

机器学习笔记之优化算法(十一)凸函数铺垫:梯度与方向导数
机器学习笔记之优化算法——凸函数铺垫:梯度与方向导数 引言回顾:偏导数方向余弦方向导数方向导数的几何意义方向导数的定义 方向导数与偏导数之间的关联关系证明过程 梯度 ( Gradient ) (\text{Gradient}) (Gradient) 引言 本节作为介绍凸函数的铺垫&a…...
探究Vue源码:mustache模板引擎(11) 递归处理循环逻辑并收尾算法处理
好 在上文 探究Vue源码:mustache模板引擎(10) 解决不能用连续点符号找到多层对象问题,为编译循环结构做铺垫 我们解决了js字符串没办法通过 什么点什么拿到对象中的值的问题 这个大家需要记住 因为这个方法的编写之前是当做面试题出现过的 那么 本文 我们就要去写上…...
STM32 CubeMX USB_CDC(USB_转串口)
STM32 CubeMX STM32 CubeMX 定时器(普通模式和PWM模式) STM32 CubeMX一、STM32 CubeMX 设置USB时钟设置USB使能UBS功能选择 二、代码部分添加代码实验效果 printf发…...
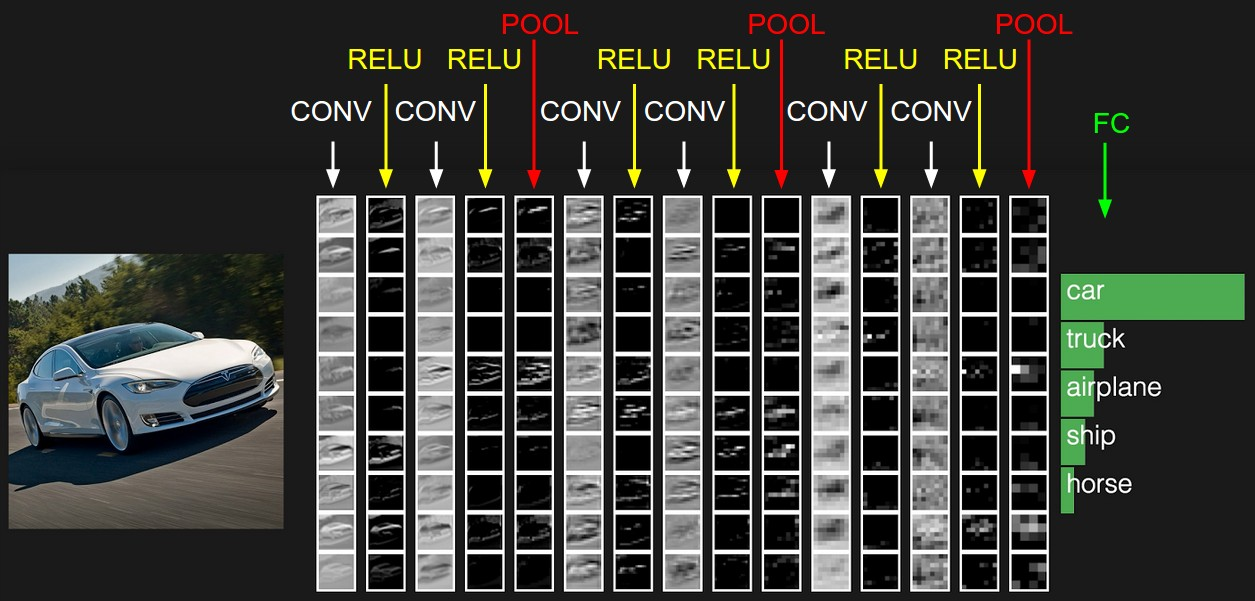
机器学习——卷积神经网络基础
卷积神经网络(Convolutional Neural Network:CNN) 卷积神经网络是人工神经网络的一种,是一种前馈神经网络。最早提出时的灵感来源于人类的神经元。 通俗来讲,其主要的操作就是:接受输入层的输入信息&…...
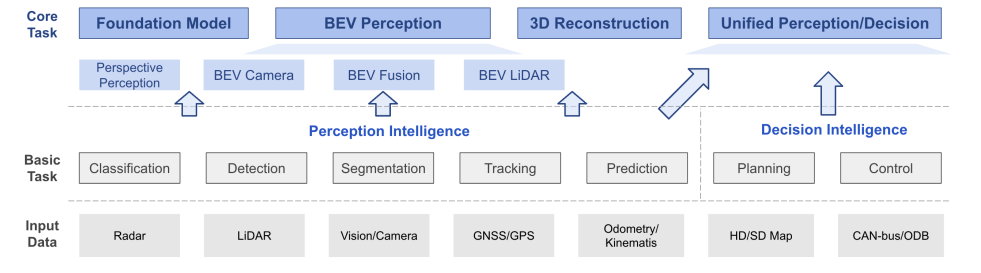
端到端自动驾驶前沿论文盘点(pdf+代码)
现在的自动驾驶,大多数还是采用的模块化架构,但这种架构的缺陷十分明显:在一个自动驾驶系统里,可能会包含很多个模型,每个模型都要专门进行训练、优化、迭代,随着模型的不断进化,参数量不断提高…...
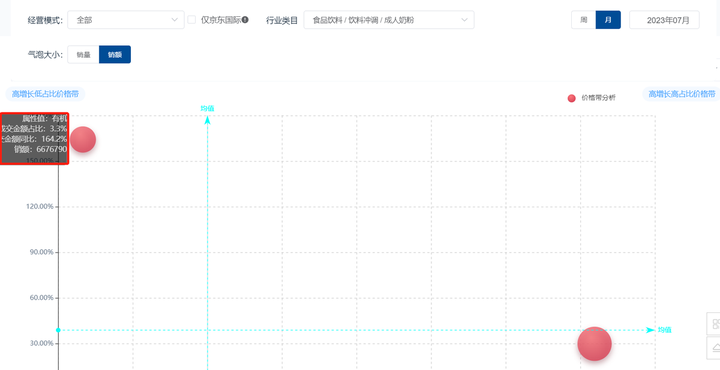
2023年中期奶粉行业分析报告(京东数据开放平台)
根据国家统计局和民政部数据公布,2022年中国结婚登记数创造了1980年(有数据公布)以来的历史新低,共计683.3万对。相较于2013年巅峰时期的数据,2022年全国结婚登记对数已接近“腰斩”。 2023年“520”期间的结婚登记数…...

web集群学习:基于CentOS 7构建 LVS-DR 群集并配置服务启动脚本
目录 1、环境准备 2、配置lvs服务启动脚本 1、在RS上分别配置服务启动脚本 2、在lvs director上配置服务启动脚本 3、客户端测试 配置LVS-DR模式主要注意的有 1、vip绑定在RS的lo接口; 2、RS做arp抑制; 1、环境准备 VIP192.168.95.10 RS1192.168…...

Flask 高级应用:使用蓝图模块化应用和 JWT 实现安全认证
本文将探讨 Flask 的两个高级特性:蓝图(Blueprints)和 JSON Web Token(JWT)认证。蓝图让我们可以将应用模块化,以便更好地组织代码;而 JWT 认证是现代 Web 应用中常见的一种安全机制。 一、使用…...
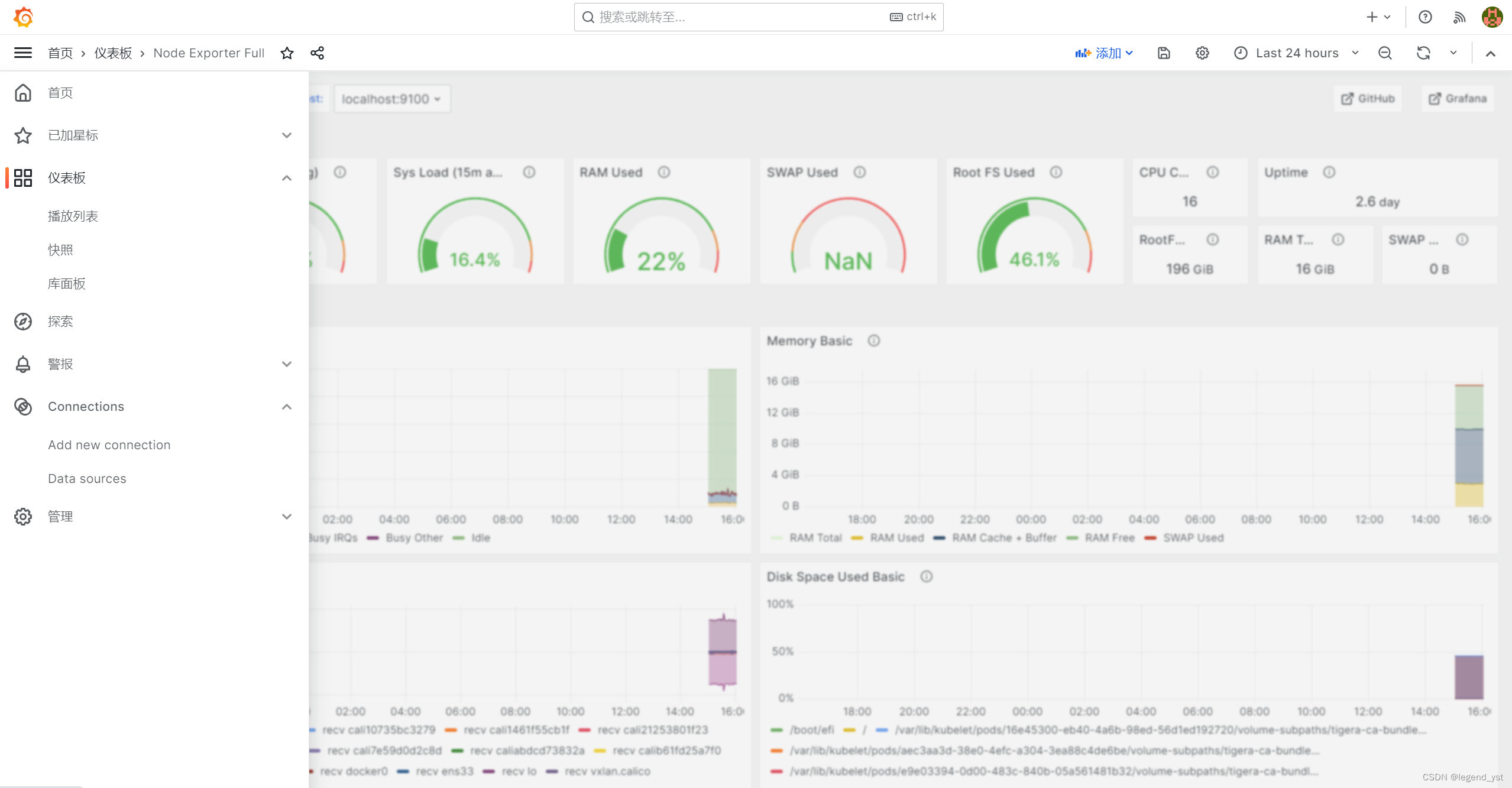
【Grafana】中文界面配置 v10.0.3
比如通过 docker run -d -p 3000:3000 -v /e/code/monitor/grafana/grafana.ini.txt:/etc/grafana/grafana.ini grafana/grafana运行一个容器(最新是v10.0.3)。 在 /admin/settings 可以看到 users 部分有一个 default_language 配置。 所以在挂载到 …...

web前端html
文章目录 快捷方式一、html5的声明二、html5基本骨架 2.1 html标签 2.2 head标签 2.3 body和head同级 2.4 body标签 2.5 title标签 2.6 meta标签 三、标题标签介绍与应用 3.1 标题的介绍 3.2 标题标签位置摆放 3.3 标签之段落、换行、水平线 3.3 标签之图片 3.3.1 图…...
Unity 编辑器选择器工具类Selection 常用函数和用法
Unity 编辑器选择器工具类Selection 常用函数和用法 点击封面跳转下载页面 简介 在Unity中,Selection类是一个非常有用的工具类,它提供了许多函数和属性,用于操作和管理编辑器中的选择对象。本文将介绍Selection类的常用函数和用法ÿ…...
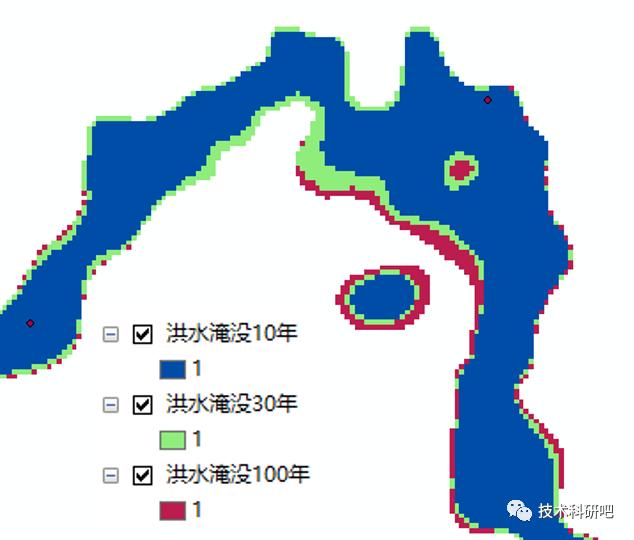
ArcGIS在洪水灾害普查、风险评估及淹没制图中应用教程
详情点击链接:ArcGIS在洪水灾害普查、风险评估及淹没制图中应用教程 一:洪水普查技术规范 1.1 全国水旱灾害风险普查实施方案 1.2 洪水风险区划及防治区划编制技术要求 1.3 山丘区中小河流洪水淹没图编制技术要求 二:ArcGIS及数据管理 …...

Oracle日志相关操作
1.归档日志设置 # 切换账号 $ su - oracle# 登录oracle的sys账户 $ sqlplus / as sysdbasql> archive log list; #查看是不是归档方式 SQL> archive log list; Database log mode Archive Mode Automatic archival Enabled Archive destin…...
IMV8.0
一、背景内容 经历了多个版本,基础内容在前面,可以使用之前的基础环境: v1: https://blog.csdn.net/wtt234/article/details/132139454 v2: https://blog.csdn.net/wtt234/article/details/132144907 v3: h…...

【Linux 网络】 数据链路层协议
数据链路层协议 数据链路层解决的问题以太网协议认识以太网以太网帧格式 认识MAC地址对比理解MAC地址和IP地址认识MTUMTU对IP协议的影响MTU对UDP协议的影响MTU对于TCP协议的影响ARP协议ARP协议的作用ARP协议的工作流程ARP数据报的格式 总结 数据链路层解决的问题 IP拥有将数据跨…...
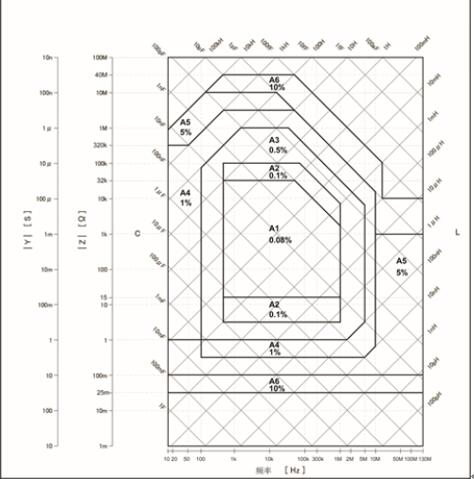
GWJDN-400型2MHZ自动平衡高温介电温谱仪
GWJDN-400型2MHZ自动平衡高温介电温谱仪 GWJDN-400型2MHZ自动平衡高温介电温谱仪 关键词:介电常数,高温介电,自动平衡 主要功能: 材料介电常数测试仪 半导体材料的介电常数、导电率和C-V特性液晶材料:液晶单元的介电常数、弹性…...

第十五次CCF计算机软件能力认证
第一题:小明上学 小明是汉东省政法大学附属中学的一名学生,他每天都要骑自行车往返于家和学校。 为了能尽可能充足地睡眠,他希望能够预计自己上学所需要的时间。 他上学需要经过数段道路,相邻两段道路之间设有至多一盏红绿灯。 京…...

ThreadPoolExecutor线程池详解
ThreadPoolExecutor线程池详解 1. 背景 项目最近的迭代中使用到了ThreadPoolExecutor线程池,之前都只是知道怎么用,没有了解过线程池的底层原理,项目刚上线,有时间整理一下线程池的用法,学习一下线程池的底层实现与工…...
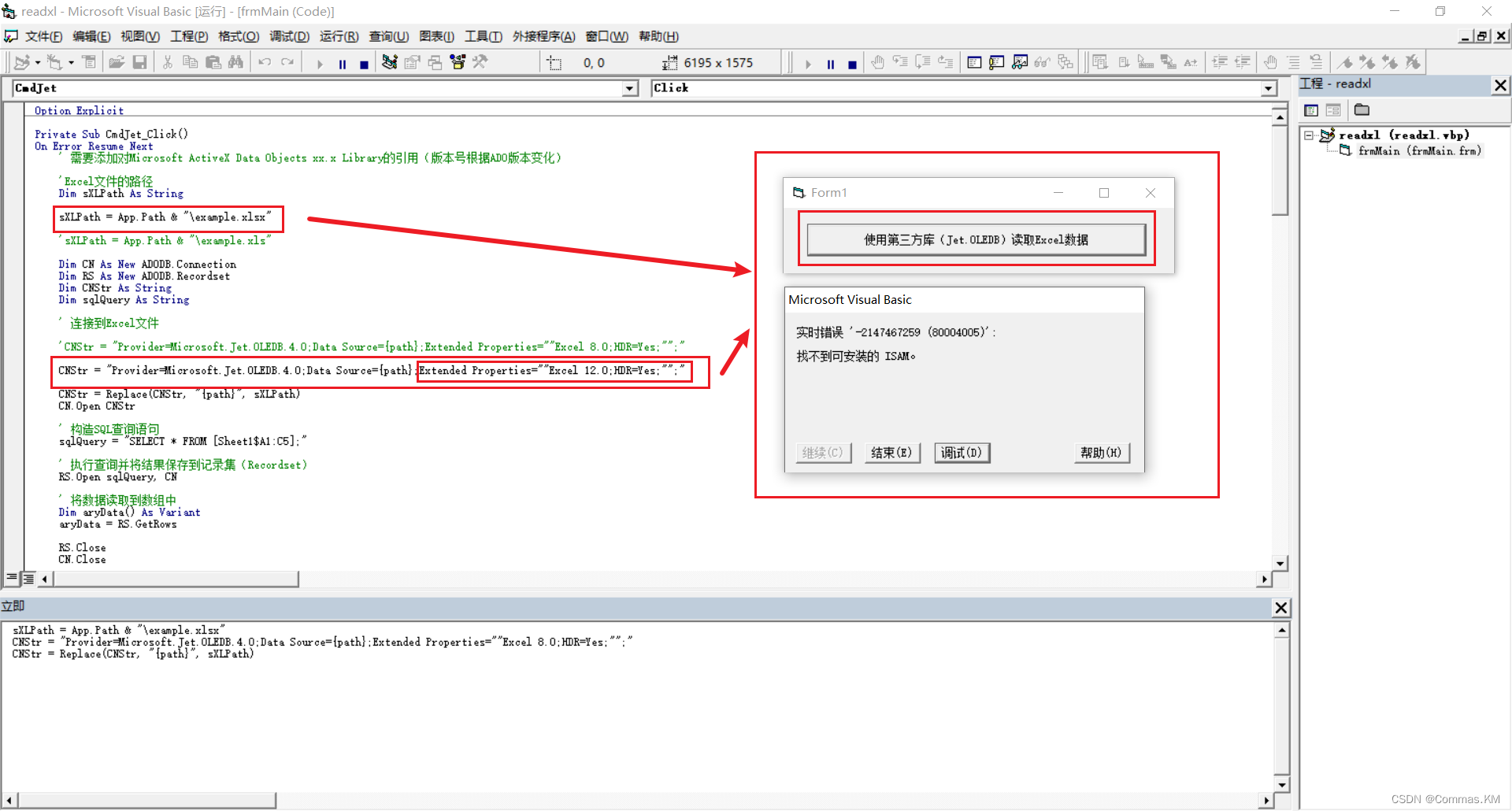
【VB6|第22期】用SQL的方式读取Excel数据
日期:2023年8月7日 作者:Commas 签名:(ง •_•)ง 积跬步以致千里,积小流以成江海…… 注释:如果您觉得有所帮助,帮忙点个赞,也可以关注我,我们一起成长;如果有不对的地方ÿ…...
融云:从「对话框」跳进魔法世界,AIGC 带给社交的新范式
8 月 17 日(周四),融云将带来直播课-《北极星如何协助开发者排查问题与预警风险?》欢迎点击上方报名~ AIGC 与社交结合的应用主要分两种,一是发乎于 AIGC,以大模型为基础提供虚拟伴侣等服务的 Appÿ…...

地震勘探——干扰波识别、井中地震时距曲线特点
目录 干扰波识别反射波地震勘探的干扰波 井中地震时距曲线特点 干扰波识别 有效波:可以用来解决所提出的地质任务的波;干扰波:所有妨碍辨认、追踪有效波的其他波。 地震勘探中,有效波和干扰波是相对的。例如,在反射波…...

超短脉冲激光自聚焦效应
前言与目录 强激光引起自聚焦效应机理 超短脉冲激光在脆性材料内部加工时引起的自聚焦效应,这是一种非线性光学现象,主要涉及光学克尔效应和材料的非线性光学特性。 自聚焦效应可以产生局部的强光场,对材料产生非线性响应,可能…...

SciencePlots——绘制论文中的图片
文章目录 安装一、风格二、1 资源 安装 # 安装最新版 pip install githttps://github.com/garrettj403/SciencePlots.git# 安装稳定版 pip install SciencePlots一、风格 简单好用的深度学习论文绘图专用工具包–Science Plot 二、 1 资源 论文绘图神器来了:一行…...

cf2117E
原题链接:https://codeforces.com/contest/2117/problem/E 题目背景: 给定两个数组a,b,可以执行多次以下操作:选择 i (1 < i < n - 1),并设置 或,也可以在执行上述操作前执行一次删除任意 和 。求…...

[10-3]软件I2C读写MPU6050 江协科技学习笔记(16个知识点)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16...

Spring AI与Spring Modulith核心技术解析
Spring AI核心架构解析 Spring AI(https://spring.io/projects/spring-ai)作为Spring生态中的AI集成框架,其核心设计理念是通过模块化架构降低AI应用的开发复杂度。与Python生态中的LangChain/LlamaIndex等工具类似,但特别为多语…...

通过 Ansible 在 Windows 2022 上安装 IIS Web 服务器
拓扑结构 这是一个用于通过 Ansible 部署 IIS Web 服务器的实验室拓扑。 前提条件: 在被管理的节点上安装WinRm 准备一张自签名的证书 开放防火墙入站tcp 5985 5986端口 准备自签名证书 PS C:\Users\azureuser> $cert New-SelfSignedCertificate -DnsName &…...

如何配置一个sql server使得其它用户可以通过excel odbc获取数据
要让其他用户通过 Excel 使用 ODBC 连接到 SQL Server 获取数据,你需要完成以下配置步骤: ✅ 一、在 SQL Server 端配置(服务器设置) 1. 启用 TCP/IP 协议 打开 “SQL Server 配置管理器”。导航到:SQL Server 网络配…...

微服务通信安全:深入解析mTLS的原理与实践
🔥「炎码工坊」技术弹药已装填! 点击关注 → 解锁工业级干货【工具实测|项目避坑|源码燃烧指南】 一、引言:微服务时代的通信安全挑战 随着云原生和微服务架构的普及,服务间的通信安全成为系统设计的核心议题。传统的单体架构中&…...

Mac flutter环境搭建
一、下载flutter sdk 制作 Android 应用 | Flutter 中文文档 - Flutter 中文开发者网站 - Flutter 1、查看mac电脑处理器选择sdk 2、解压 unzip ~/Downloads/flutter_macos_arm64_3.32.2-stable.zip \ -d ~/development/ 3、添加环境变量 命令行打开配置环境变量文件 ope…...
